Abstract
The nuclear reaction rate formula used in stellar evolution calculation is carefully examined. A uniform expansion is performed up to fourth order in the relevant physical parameter. The convergence of the series is assessed and a semianalytical expression is derived, valid for all values of the expansion parameter. The formulae with electron screening and plasma dissipative collision effects are also evaluated. The agreement of the approximate analytical formulae with the exact result is excellent over a wide range of values of the parameters
Uniform Expansion of the Thermonuclear Reaction Rate Formula* * Supported in part by the CNPq.
M.S. Hussein and M.P. Pato
Nuclear Theory and Elementary Particle Phenomenology Group
Instituto de Física, Universidade de São Paulo
CP 66318, 05389-970 São Paulo, SP, Brazil
Received April 19, 1997
The nuclear reaction rate formula used in stellar evolution calculation is carefully examined. A uniform expansion is performed up to fourth order in the relevant physical parameter. The convergence of the series is assessed and a semianalytical expression is derived, valid for all values of the expansion parameter. The formulae with electron screening and plasma dissipative collision effects are also evaluated. The agreement of the approximate analytical formulae with the exact result is excellent over a wide range of values of the parameters.
I. Introduction
To obtain the rate of nuclear energy production in the stellar interior one integrates the nuclear reaction cross section over the thermal distribution of nuclei. Closed expressions for the rate formula are desirable for speedy calculation of the stellar evolution and element abundances. It is a common practice to obtain these expressions within the Gaussian approximation [1]. Recently, Anderson, Haubold and Mathai [2] have developed a series expansion of the rate integrals using the gamma function and complex integration. In this paper we develop a new type of series based on a judicious choice of Gaussian mapping and using the method of uniform approximation. The series we obtain are rapidly convergent and avoid several of the singularities encountered in [2]. Further, the different terms in the series are explicitly given in terms of the parameters of the integral (electron screening energy, Gamow energy, etc.).
Our results are certainly relevant for the calculation of the rate of the reaction 12C (a, g)16O ® in massive stars with  . This last reaction is known to be dominated by nearby above-threshold and sub-threshold resonances making the astrophysical S -factor deviate considerably from a second order expansion in energy. It is known that the rate of this reaction, which dominates the scenario of the evolution of a massive star into a type II supernova, should be known to better than 20% [1]. Thus more precise analytical closed formulae are welcome here.
. This last reaction is known to be dominated by nearby above-threshold and sub-threshold resonances making the astrophysical S -factor deviate considerably from a second order expansion in energy. It is known that the rate of this reaction, which dominates the scenario of the evolution of a massive star into a type II supernova, should be known to better than 20% [1]. Thus more precise analytical closed formulae are welcome here.
The paper is organized as follows. In Section II the reaction rate formula for bare nuclei are calculated to fourth-order in the Gamow energy. The effect of electron screening and plasma collision loss are then considered and the corresponding integrals are evaluated in Section III. Finally in Section V we discuss our result in connection with the rates of several reactions and give some concluding ramarks.
II. II. Expressions for the thermonuclear reaction rate formula
The reaction rate formula is given by
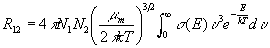
where Ni is the number density of nucleus i , mm is the reduced mass of the two-nucleus system, kT is the thermal energy and v is the relative velocity. Changing variables from v to E through  , and using the usual low-energy form of the cross section,
, and using the usual low-energy form of the cross section,
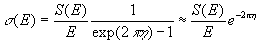 ,
, where  is the Sommerfeld parameter, we have, with
is the Sommerfeld parameter, we have, with 
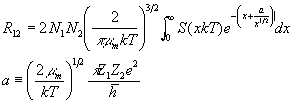
For non-resonant reactions, S(E) is slowly varying and may be expanded
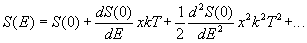 .
. Therefore Eq. (3) may be written as
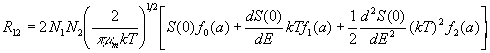 ,
, where the functions fn(a) are defined by
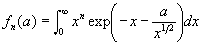 .
. Setting y º x n + 1, we can rewrite (6) as
 .
.
Thus an exact series representation of R12 is
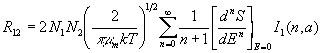 .
. In the following, we develop the uniform series for fn(a) . For this purpose we recall some known facts about the uniform expansion of integrals of the general form [3],
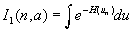
where Hn(u) is given by
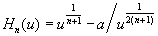 ,
, which has an extremum at  . Introducing the mapping
. Introducing the mapping
where t = 0 correspondents to  with un being the position of the extremum, given above, we can now write
with un being the position of the extremum, given above, we can now write
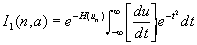 .
. Expanding  in powers of t and integrating, we find
in powers of t and integrating, we find
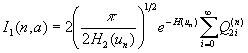 ,
, where the first four terms in the sum are
 ,
, where  . From Eq. (10), we then find
. From Eq. (10), we then find
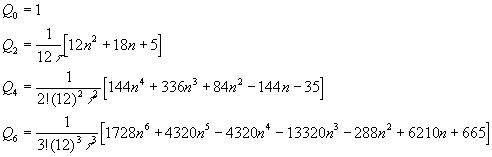
The integral of Eq. (6) can now be evaluated straightforwardly using the above formulae. The functions f0(a), f1(a) and f2(a) are then easily found, up to the fourth order term,
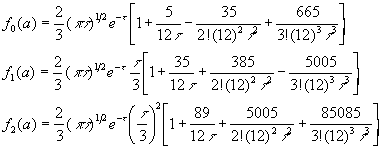
where
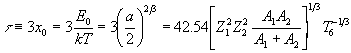 ,
, where Eis the Gamow energy.
In Fig. 1 we show the relative error of (16) in comparison with the exact numerical result. It is clear that (16) is an excellent approximation.
The expression for f0(a) up to the third term has been evaluated by Salpeter [4] and is quoted in textbooks [1]. The first term in f1(a) was calculated by Bahcall [5]. The other terms in fand f1 and the function f2(a) are new results. We feel that f1 and f2 (and possibly other integrals) may be important for stellar evolution calculation involving nuclear reactions near threshold when S(E) would have significant energy variation.
Figure 1. The relative error defined as |fn, exact(t) - fn, Eq. (16)(t)|/fn, exact(t) vs. t. The small oscillations are numerical uncertainty in the evaluation of fn, exact(t) .
In order to assess the convergence of the series in (6), we consider the complex solutions of the equation that determines the position of the maximum in the integrand of Eq. (6). The following discussion applies to any n . We therefore consider the case n = 0 . The extremum condition reads
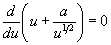 .
. We find one real solution, which was used previously in evaluating the integral,  , and two complex conjugate solutions given by
, and two complex conjugate solutions given by
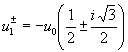 .
. The function, H(u) , acquires the following values at uand 
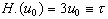
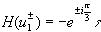 .
. The radius of convergence is measured by [3]
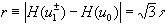 .
.Thus, the series is convergent up to the term of order  , which is usually large for typical values of the parameters t (say, 10). Recent work of Berry [6], shows how to estimate the rest of the series starting at the
, which is usually large for typical values of the parameters t (say, 10). Recent work of Berry [6], shows how to estimate the rest of the series starting at the  'th term.
'th term.
Figure 2. The integral I1(n,a) vs. a . The upper curve is that exact result which is reproduced with our formula. The lower curve in the result of Ref. [2].
In Fig. 2 we show the result of our calculation of I1 , for S = S(0) , based on Equation (13), taking up to the fourth order terms in f0(a) , compared to the exact numerical integration result (difficult to distinguish from the approximate one) for a wide range of value of t. The lower curve in the figure is the result of Ref. [2]. It is clear that our procedure is quite accurate.
III. Effect of electron screening and plasma dissipation
We turn now to the more realistic case that includes the effect of electron screening. This effect can be taken into account by a shift in the energy of the fusing nucleus, Ec.m.® Ec.m. + Ue when Ue is roughly given by  , with Ra being the atomic radius. The shielded nuclei clearly feel a lower Coulomb barrier when they fuse, which is equivalent to the energy shift above. The value of Ue varies with the system. For p + p , Ue ~ 29eV, when as for a + 12C, Ue = 2.07 keV.
, with Ra being the atomic radius. The shielded nuclei clearly feel a lower Coulomb barrier when they fuse, which is equivalent to the energy shift above. The value of Ue varies with the system. For p + p , Ue ~ 29eV, when as for a + 12C, Ue = 2.07 keV.
With screening, the thermonuclear reaction rate integral becomes (using the rotation of Ref. [2])
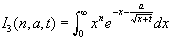 ,
, where  . The evaluation of (23) proceeds in manner similar to that used for I1 albeit with a different mapping procedure. The details can be found in Appendix I. The final result which we quote here is
. The evaluation of (23) proceeds in manner similar to that used for I1 albeit with a different mapping procedure. The details can be found in Appendix I. The final result which we quote here is
where
In the above, erfc is the complementary error function and
In Appendix I we give explicit forms of the first two coefficients, band b1 . Note that  if t >
if t >  whereas
whereas  for t < y0 . Further, in the limit of no screening t = 0 and x = - ¥, which gives the desired check of Eq.(24)
for t < y0 . Further, in the limit of no screening t = 0 and x = - ¥, which gives the desired check of Eq.(24)
The above form for I3 is calculated for n = 0 , up to second order in the series of Eq. (24). The result is compared with the exact (again not distinguishable) result in Fig. 3. Also shown is the lowest order approximation which is given by
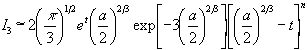
From Fig. 3 we see clearly that by performing the integral using the uniform approximation and keeping only the first two leading terms one approaches very closely the exact result. The rough estimate of Eq. (25), diverges at  .
.
Before ending this section we mention that dissipative collision processes in the stellar plasma result in a cut off of the high energy part of the Maxwell-Boltzamann distribution at a certain high energy Ed = kTd . This means that the integral I1 , is modified to
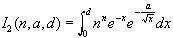
The above integral is easily related to I1 , and I'3 through
or
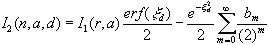 ,
, where erf is the error function.
Figure 3. The integral I3(n,a,t) vs. a and t . See text for details. The asymptotic result is shown as the broken (lower) line. The upper full curve is the exact and our results including band b1 . They are practically indistinguishable. The result with bonly is the lower curve.
IV. Discussion and conclusions
The mehod of calculation developed here allows a fast computation of the thermonuclear reaction rate using analytical formulae and a simple way of estimating the relative error when compared to the exact numerical calculation of the integral. Further, our method may allow a way of treating the wide resonance cases encountered in, e.g., the 12c(a, g)160 reaction in massive stars.
We first consider two reactions of great importance to the solar neutrino problem and the supernova event: p + p ® d + e + + v (T6 = 15) and 3He + 4He ® 7Be + g (T6 = 5000) In the first reaction the Gamow energy  which gives for
which gives for  , while the calculated S -factor is given by [1]
, while the calculated S -factor is given by [1]
The Q -value is 1.44 MeV.
In the second reaction, the Gamow energy is  and then a = 106.455 while the measured S -factor in [1]
and then a = 106.455 while the measured S -factor in [1]
We have used our approximate formulae for the non-resonant reaction rate, Eq. (5) with f0(a) and f1(a) given by Eq. (16).
The values we obtain for the rate R12 are 1.1995 x 10- 43cm 3/s and 8.81 x 10- 35cm 3/s respectively. It is instructive to measure the relative error from Fig. 1. For the p + p reaction, a = 19.63 and f0(19.63) = 5.101 x 10- 6 and f1(19.63) = 2.758 x 10- 5 . The relative error in f0 is (t = 13.691) about 8 x 10- 6 , whereae in f1 it is 2 x 10- 4 , quite small. In the 3He + 4He reaction, a = 106.455 and f0(106.455) = 2.85 x 10- 18, f1(106.455) = 4.7 x 10- 17 . The relative error in fis (t = 42.45) is 10- 6 and f1 it is 2 x 10- 5 , again quite small. The great accuracy of our approximate formulae may be of value in the solar neutrino problem [7] where it is expected that better accuracy with which S(0),S'(0) and S''(0) are extracted from the data will be attained in the future.
A more stringest test of our formulae is supplied to the so-called wide resonance case such as the one encountered in the 17C(a, g)160 reaction in massive stars. Here the S -factor deviates considerably from the polynomial of Eq. (4). In fact the measurement [8] shows that over the energy range 1.3 < Ec.m.(MeV) < 3.5 the S -factor has a Lorentzian shape. When extrapolated to the relevant astrophysical energy (Gamow energy) of 0.3 KeV (T9 = 0.1 - 0.2 ) using, reasonable theory, the final resulting S -factor has the shape of a Lorentzian peaked at Ec.m. = 2.4 MeV which sits on a background that has the shape of a Gaussian e - bE2 . The Gaussian background can be handeled using the method of consecutive mappings while the Lorentzian can be evaluated using the method of residues. We leave full discussion of this problem to a future work.
Appendix -- asymptotic series of the integral
Although the value of the screening energy, t , relevant for stellar calculation is small compared t the Gamow energy, it is still useful to find an analytical form for I3 (n,a,t) which is valid for a large range of values of t . The result for I3 which we derived and discussed in Section,
is derived in this Appendix. The sum  is rapidly convergent. In fact the result shown in Fig. (3) was obtained with only the first two terms.
is rapidly convergent. In fact the result shown in Fig. (3) was obtained with only the first two terms.
The integral we wish to calculate is
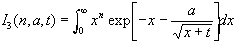 .
. A change of variable y º x + t renders I3 into
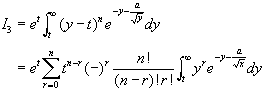 .
. Thus what is needed is the calculation of
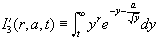
As was done in the calculation of I1 we introduce the following mapping
where
and F(y0) = 3y0 . Then
Let us call the function  . We introduce now another mapping
. We introduce now another mapping
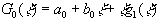
with g1(x) = 0 . As we show below, explicit knowledge of the function g1(x) is not required. With (A.9 ) we have
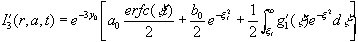 ,
,where an integration by parts has been carried out which allowed writing the last term in its present form. By repeated application of the mapping and integration by parts one can generate the series, vis
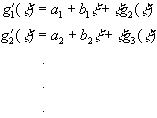
with g2(x) = g3(x) = ... = 0 .
Thus
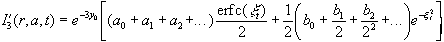 .
. Clearly in the limit t = 0, xt = - ¥ and the above function becomes
I '3(r,a,0) = e - 3y0(a0 + a1 + a2 + ... ) ,
which is nothing but I1(r,a) . Accordingly we obtain Eq. (24). Now we turn for the calculation of the coefficients a0,a1,... and b0,b1,... .
Clearly
and
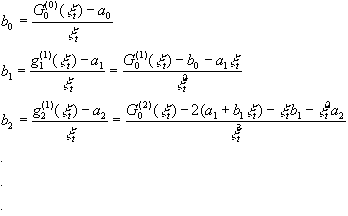
where G (n) = d nG/dxn which can be calculated from the defining relations
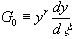
and
For example, to evaluate a0,a1,band b1 one needs to know G (0)(0), G (0)(x), G (1)0(xt) and G (2)(0) . Then
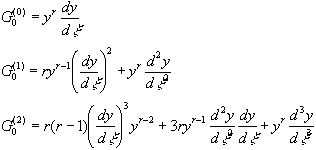 .
. The derivatives  can be obtained from F(y) . Since
can be obtained from F(y) . Since  by definition, we have
by definition, we have
In the above equations,  are given by
are given by
and
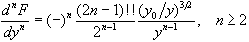 .
.The above formulae were employed in the derivation of the series expansion for I1(n,a) (Section II) and I2(n,a,d ) and I3(n,a,t) (Section III).
References
[1] See e.g., Claus E. Rolfs and William S. Rodney, "Cauldrons in the Cosmos: Nuclear Astrophysics'', The University of Chicago Press (1988) Chapter 4 (pages 150-189).
[2] W.J. Anderson, M.J. Haubold, and A.M. Mathai, Astr. and Space Science 214, 49 (1994).
[3] R.B. Dingle, "Asymptotic Expansions: their derivation and interpretation'', New York & London, Academic Press (1973).
[4] E.E. Salpeter, Phys. Rev. 88, 547 (1952).
[5] J.N. Bahcall, Ap. J. 143, 259 (1966).
[6] M.V. Berry, Proc. R. Soc. London A422, 7 (1989); M.V. Berry and C.J. Howls, Proc. R. Soc. London A434, 657 (1991).
[7] J.N. Bahcall, "Neutrino Astrophysics'' Cambridge V. Press (1990).
[8] A. Redder et al. Nucl. Phys. A462, 385 (1987)
- [1] See e.g., Claus E. Rolfs and William S. Rodney, "Cauldrons in the Cosmos: Nuclear Astrophysics'', The University of Chicago Press (1988) Chapter 4 (pages 150-189).
- [2] W.J. Anderson, M.J. Haubold, and A.M. Mathai, Astr. and Space Science 214, 49 (1994).
- [3] R.B. Dingle, "Asymptotic Expansions: their derivation and interpretation'', New York & London, Academic Press (1973).
- [4] E.E. Salpeter, Phys. Rev. 88, 547 (1952).
- [5] J.N. Bahcall, Ap. J. 143, 259 (1966).
- [6] M.V. Berry, Proc. R. Soc. London A422, 7 (1989);
- [7] J.N. Bahcall, "Neutrino Astrophysics'' Cambridge V. Press (1990).
- [8] A. Redder et al. Nucl. Phys. A462, 385 (1987)
Publication Dates
-
Publication in this collection
04 Feb 1999 -
Date of issue
Sept 1997
History
-
Received
19 Apr 1997





















