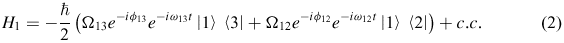Abstracts
The simultaneous propagation of two optical pulses through a doped nonlinear dispersive medium modelled by a resonant three-level system was investigated numerically, within the framework of a pair of coupled extended nonlinear Schrödinger equations. These included the contribution of the dopant resonances whose dynamics is governed by Bloch equations. In this work, we review the interesting possibilities on the manipulation of fields such as cloning, breakup and soliton interactions, that the combination of coherent population trapping with nonlinear dispersive media offers.
soliton; quantum coherence; nonlinearity; cloning
Investiga-se numericamente a propagação simultânea de dois pulsos ópticos através de um meio dispersivo não linear dopado, modelado por um sistema ressonante de três níveis, usando-se uma abordagem de equações generalizadas não lineares de Schrödinger. Estas últimas incluem a contribuição das ressonâncias do dopante cuja dinâmica é regida pelas equações de Bloch. Neste trabalho, revemos as possibilidades interessantes que a combinação de efeitos dispersivos não lineares com o aprisionamento coerente da população oferecem, tais como: clonagem, quebra e interação entre solitons.
soliton; coerência quântica; não-linearidade; clonagem
Coherent soliton propagation through doped optical fibers: cloning, breakup, and soliton interactions* * Invited paper Correspondence to: Dra. Solange B. Cavalcanti E-mail: solange@lux.ufal.br
SOLANGE B. CAVALCANTI, EDUARDO J. DA S. FONSECA,
DILSON P. CAETANO and JANDIR M. HICKMANN
Departamento de Física, Universidade Federal de Alagoas,
Cidade Universitária - 57072-970 Maceió-AL, Brazil
Manuscript received on March 23, 2001; accepted for publication on March 30, 2001;
presented by AFFONSO G. GOMES
ABSTRACT
The simultaneous propagation of two optical pulses through a doped nonlinear dispersive medium modelled by a resonant three-level system was investigated numerically, within the framework of a pair of coupled extended nonlinear Schrödinger equations. These included the contribution of the dopant resonances whose dynamics is governed by Bloch equations. In this work, we review the interesting possibilities on the manipulation of fields such as cloning, breakup and soliton interactions, that the combination of coherent population trapping with nonlinear dispersive media offers.
Key words: soliton, quantum coherence, nonlinearity, cloning.
1. INTRODUCTION
Quantum interference in coherently prepared atomic systems has lead to dramatic new effects such as laser without inversion and electromagnetic induced transparency (EIT) (Harris 1997). The latter is an effect that permits the propagation of light through an otherwise opaque atomic medium. Spectacular examples of quantum coherence effects have been provided by recent reports on extremely slow group velocities (Hau et al. 1999) and light pulse localization and containment within an atomic cloud (Liu et al. 2001).
The remarkable discovery of self induced transparency (SIT) has elucidated many physical interesting propagation properties predicted by the area theorem, concerning the area of the pulse defined as,  =
= 
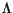 -scheme as depicted in Fig. 1. The cloning process here is understood as the amplification and shaping of a weak field of arbitrary profile at the signal frequency (
-scheme as depicted in Fig. 1. The cloning process here is understood as the amplification and shaping of a weak field of arbitrary profile at the signal frequency ( 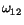 ) into a replica of a soliton at the pump transition (
) into a replica of a soliton at the pump transition ( 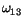 ). The physical mechanism behind most of these unexpected phenomena is known as coherent population trapping (CPT) (Alzetta et al. 1976). These trapping states are stationary states, also known as dark states of the Hamiltonian, which do not evolve in the presence of the radiative relaxation of the system.
). The physical mechanism behind most of these unexpected phenomena is known as coherent population trapping (CPT) (Alzetta et al. 1976). These trapping states are stationary states, also known as dark states of the Hamiltonian, which do not evolve in the presence of the radiative relaxation of the system.
Solitons are also present in dispersive nonlinear waveguides with great perspectives for high-rate and long-distance communications systems (Agrawal 1992). The propagation of soliton pulses through dispersive nonlinear media, the so-called nonlinear Schrödinger soliton (NLS-soliton), has been another field of great interest in recent years not only from theoretical aspects but also from the technological developments that it might provide. The idea to extend those new exciting experiments based on CPT to nonlinear Kerr media, should prove itself worthwhile. The coexistence of both solitons, named the NLS-SIT-soliton, has already been investigated in two-level media (Maimistov and Manykin 1983, Nakazawa et al. 1991a). Experiments using an Erbium-doped fiber waveguide (Nakazawa et al. 1991b, Nakazawa et al. 1991c) have been carried out exhibiting the breakup of stable 2p, 4p and multiple soliton pulses. Furthermore, coherent p-pulse propagation in an Erbium-doped fiber waveguide amplifier showing pulse breakup has been observed.
In this work, we review the effects of the propagation of a SIT-NLS soliton in a three-level atomic system, with the inclusion of the nonlinear term of cross-phase modulation, coupling through the Kerr effect both fields. To this end, we study the propagation properties of pulses that travel in a doped, nolinear and dispersive waveguide as for example an optical fiber. By solving a system of five coupled equations involving the three coefficients of the atomic wave function representing the quantum levels and two extended NLS governing the fields propagation, we shall discuss in the following sections numerical experiments involving various SIT-NLS inputs that reveal interesting behaviour such as: soliton cloning, soliton breakup and soliton interactions.
2. BASIC THEORY
We consider the interaction of a three-level atomic system with two fields, described by the Hamiltonian H = H0 + H1. Here, the free Hamiltonian
is perturbed by the fields according with
where
e-i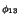 and
and 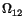 e-i
e-i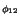 are the complex Rabi frequencies associated with the coupling of the field modes of frequencies
are the complex Rabi frequencies associated with the coupling of the field modes of frequencies 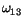 and
and 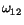 , resonant with the dipole allowed atomic transitions
, resonant with the dipole allowed atomic transitions 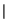 1
1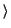
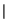 3
3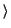 and
and 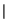 1
1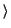
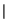 2
2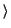 respectively. The time dependent atomic wave functions are written as
respectively. The time dependent atomic wave functions are written as
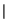
(3)
Using Schrödinger's equation, H
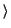 = i
= i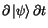 and H0i
and H0i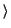 =
= 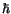 i
i (i = 1, 2, 3) we obtain the dynamical behaviour of the probability amplitudes ci(t), i.e.
(i = 1, 2, 3) we obtain the dynamical behaviour of the probability amplitudes ci(t), i.e.
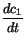 =
= 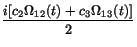
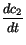 =
= 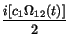
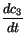 =
= 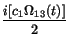
where  (t) =
(t) =  with Aij as the slowly varying amplitudes that compose the incident total electric field, i.e.
with Aij as the slowly varying amplitudes that compose the incident total electric field, i.e.

(7)
with kijc =  .
.  and
and  are the electrical dipole moments related to the associated transitions i.e.
are the electrical dipole moments related to the associated transitions i.e. 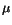 ij =
ij =  i
i
 and we have chosen
and we have chosen 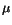 12 =
12 = 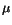 13 =
13 = 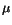
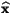 .
.
The electric field in our context is treated as a classical wave, which is a good approximation for the coherent state of light produced by a pulsed laser necessary to perform the experiments, to corroborate the numerical results obtained here. Therefore, wave propagation is considered within the framework of extended nonlinear Schrödinger (NLS) equations, that include the contribution of the three-level resonant system to the polarization, P = tr(
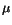 ) where
) where  is the density matrix. The usual NLS equation that describes the propagation of an electromagnetic field through a nonlinear dispersive medium in the absence of resonances, as for example an optical fiber, is given by
is the density matrix. The usual NLS equation that describes the propagation of an electromagnetic field through a nonlinear dispersive medium in the absence of resonances, as for example an optical fiber, is given by
 = -
= -
(8)
where  is the group velocity dispersion parameter and we have introduced
is the group velocity dispersion parameter and we have introduced  , the nonlinear parameter
, the nonlinear parameter  = n2k with n2 as the Kerr index and k as the wave vector. This equation belongs to a special class of completely integrable equations with exact soliton solutions derived from the inverse scattering method (Gardner et al. 1967). Among these solutions, a special role is played by those solitons whose initial amplitude at z = 0 is given by,
= n2k with n2 as the Kerr index and k as the wave vector. This equation belongs to a special class of completely integrable equations with exact soliton solutions derived from the inverse scattering method (Gardner et al. 1967). Among these solutions, a special role is played by those solitons whose initial amplitude at z = 0 is given by,
E(0, t) = N
sech(t),where the soliton order N is an integer. The fundamental soliton corresponds to the case N = 1 while higher order solitons correspond to N > 1. The peak power necessary to launch a Nth -order soliton is N2times of that required for the fundamental soliton. An interesting property of higher order solitons is that they follow a periodic evolution pattern with the same period z0, i.e., the pulse shape goes through contraction and splitting phases until it returns to its original shape at the end of the soliton period z0.
When two optical waves of different frequencies co-propagate in a medium and interact nonlinearly through the medium, the propagation equations can be considered together via two coupled NLS-like equations. In the presence of resonances, one must take into account their contribution. Therefore, the extended NLS equations that describe the propagation of the envelope of our two optical fields through a nonlinear medium in the presence of na resonant atoms per unit volume are given by (Caetano et al. 1998):
 = -
= -
(9)
 = -
= -
(10)
This system of five coupled equations is studied numerically using a combination of the well-known split-step algorithm to solve the NLS equations, with a Runge-Kutta algorithm to solve the Bloch equations. The results of the simulations are described in the next section.
3. RESULTS
3.1. SOLITION CLONING AND BREAKUP
Let us begin by choosing the following initial configuration: a 2p - (N = 1) soliton, that is, a soliton of area 2p and order N = 1 at the pump frequency and a weaker signal. These pulses are represented by A13(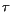 ) =
) = 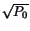
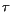 and A12(
and A12(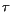 ) = rsech
) = rsech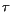 , respectively. The coordinate
, respectively. The coordinate 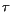 represents a normalized time for the initial pulse duration in a Galilean frame of reference, i.e.
represents a normalized time for the initial pulse duration in a Galilean frame of reference, i.e. 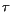 =
= 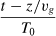 with T0 as the pulse width and vg as a mean group velocity. We introduce the parameter
with T0 as the pulse width and vg as a mean group velocity. We introduce the parameter 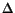 to represent the intensity ratio between pump and signal at the input, i.e.
to represent the intensity ratio between pump and signal at the input, i.e. 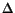 =
= 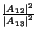 = r2. We consider the initial conditions c1 = 0, c2 = 0, c3 = - 1 so that the population is in the ground state to start with. As demonstrated in the literature (Maimistov and Manikin 1983), the condition for the coexistence of the SIT-NLS soliton is that, the amplitude and duration of a 2p-SIT pulse should be the exact ones that allow the corresponding self phase modulation to balance the dispersion spread of the pulse. Therefore, the parameters must be arranged in such a way that the input power P0 satisfies the coexistence condition
= r2. We consider the initial conditions c1 = 0, c2 = 0, c3 = - 1 so that the population is in the ground state to start with. As demonstrated in the literature (Maimistov and Manikin 1983), the condition for the coexistence of the SIT-NLS soliton is that, the amplitude and duration of a 2p-SIT pulse should be the exact ones that allow the corresponding self phase modulation to balance the dispersion spread of the pulse. Therefore, the parameters must be arranged in such a way that the input power P0 satisfies the coexistence condition 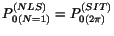 (Nakazawa et al. 1991a). We turn to Figs. 2(a) and 2(b) where we have plotted the intensity profiles of pump and signal respectively, as functions of z/z0 and
(Nakazawa et al. 1991a). We turn to Figs. 2(a) and 2(b) where we have plotted the intensity profiles of pump and signal respectively, as functions of z/z0 and 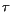 . We may observe a cloning process whereupon a soliton at the pump frequency disappears, reappearing at the signal frequency. Note that while the pump is being attenuated, the small signal assumes the shape and properties of the soliton pump. At this stage the newly created soliton begins to propagate freely undistorted and without being absorbed. The medium has become transparent to the cloned SIT-NLS soliton.
. We may observe a cloning process whereupon a soliton at the pump frequency disappears, reappearing at the signal frequency. Note that while the pump is being attenuated, the small signal assumes the shape and properties of the soliton pump. At this stage the newly created soliton begins to propagate freely undistorted and without being absorbed. The medium has become transparent to the cloned SIT-NLS soliton.
Let us now raise the power of the pump and consider a 4p - (N = 2) soliton using the same forms as used previously for both pump and signal. We refer to Figs. (3a) and (3b) where we have depicted the intensity profiles of pump and signal respectively, as functions of the normalized propagation distance z/z0 and of the normalized time 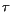 . Fig. (3a) shows that during the first stage, due to the interaction between the nonlinearity and group velocity dispersion associated to the NLS equation, a N = 2 soliton is excited but for a very short time. The SIT component quickly dominates inducing the pump pulse to breakup into two 2p solitary waves. Subsequently, we note that while both splitted waves undergo strong attenuation the signal is simultaneously amplified into two 2p solitary waves with the same properties as the waves just absorbed at the pump frequency, demonstrating that the energy of the pump has been transferred to the former pair (Caetano et al. 2000). It is important to compare our results with the results in the literature. The three-level configuration has provided the cloning process of the pair, a result obtained previously for a SIT soliton (Vemuri et al. 1997). It should be noted that this result would have not occurred in a two-level system (Nakazawa et al. 1991a). Furthermore, an important physical aspect is observed by considering the combined SIT-NLS effect after the energy transfer process is completed. At this stage, the pump is gone and the pair travels unaltered in the absence of the NLS component, as depicted in Fig. (4a). By contrast, in the presence of nonlinear dispersive effects Fig. (4b), the amplitude of the taller pulse displays a small oscillation whose period is approximate z0, so that one may identify this periodicity with the characteristic NLS soliton period [inset - Fig. (4b)]. Consequently the areas of both pulses oscillate around the 2p value (Fonseca et al. 2001).
. Fig. (3a) shows that during the first stage, due to the interaction between the nonlinearity and group velocity dispersion associated to the NLS equation, a N = 2 soliton is excited but for a very short time. The SIT component quickly dominates inducing the pump pulse to breakup into two 2p solitary waves. Subsequently, we note that while both splitted waves undergo strong attenuation the signal is simultaneously amplified into two 2p solitary waves with the same properties as the waves just absorbed at the pump frequency, demonstrating that the energy of the pump has been transferred to the former pair (Caetano et al. 2000). It is important to compare our results with the results in the literature. The three-level configuration has provided the cloning process of the pair, a result obtained previously for a SIT soliton (Vemuri et al. 1997). It should be noted that this result would have not occurred in a two-level system (Nakazawa et al. 1991a). Furthermore, an important physical aspect is observed by considering the combined SIT-NLS effect after the energy transfer process is completed. At this stage, the pump is gone and the pair travels unaltered in the absence of the NLS component, as depicted in Fig. (4a). By contrast, in the presence of nonlinear dispersive effects Fig. (4b), the amplitude of the taller pulse displays a small oscillation whose period is approximate z0, so that one may identify this periodicity with the characteristic NLS soliton period [inset - Fig. (4b)]. Consequently the areas of both pulses oscillate around the 2p value (Fonseca et al. 2001).
3.2. COHERENT POPULATION TRAPPING
We now turn to Figs. 5(a), (b) and (c) where the population dynamics corresponding to the propagation of the 2p soliton is illustrated. Notice that, while the energy transfer process occurs, the population leaves the ground state and gets back to it, to remain there afterwards, characterizing the trapping of the population at the lowest level. By considering the analytical solutions of equations (4), (5) and (6) for the particular initial configuration used above, that is,
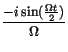
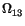
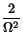
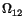
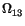 sin2
sin2
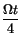
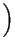
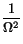
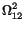 +
+ 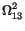 cos
cos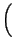
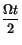
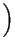
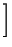
where  stands for the Rabi frequency correspondent to the field Aij and
stands for the Rabi frequency correspondent to the field Aij and  =
=  , one may conclude that by the time the pump is gone, that is, as
, one may conclude that by the time the pump is gone, that is, as 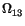
 0,
0,  c1
c1
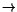 0,
0, 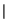 c2
c2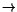 0,
0, 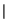 c3
c3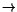 1, which means that the populations in levels
1, which means that the populations in levels 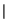 1
1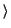 and
and 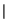 2
2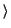 become zero and the entire population settles in level
become zero and the entire population settles in level  3
3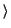 , characterizing population trapping. The cloning process occurs while the system is being driven to the trapping state by the combined action of a strong pump and a weak signal. Finally, by the time that the system returns to the lowest level the pump has gone and there is no possibility to promote the population. On the other hand, the remaining signal has dragged the energy but the levels connected by it are empty and the system becomes transparent explaining why the soliton propagates freely once the trapping is established, as seen previously. For a 4p - (N = 2) soliton, this process is doubled, as illustrated in Fig. 6(a), 6(b) and 6(c). In this case when the population returns for the first time to level
, characterizing population trapping. The cloning process occurs while the system is being driven to the trapping state by the combined action of a strong pump and a weak signal. Finally, by the time that the system returns to the lowest level the pump has gone and there is no possibility to promote the population. On the other hand, the remaining signal has dragged the energy but the levels connected by it are empty and the system becomes transparent explaining why the soliton propagates freely once the trapping is established, as seen previously. For a 4p - (N = 2) soliton, this process is doubled, as illustrated in Fig. 6(a), 6(b) and 6(c). In this case when the population returns for the first time to level 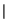 3
3 there is still energy available to promote it again and that is why 4p pulses split in two 2p pulses. By varying the relation between the intensities of pump and signal, one may accelerate the cloning process in such a way that it may occur after the breakup as we show in Fig. 7 where the propagation of the pump pulse as well as the signal is illustrated during the first z0 for ratio intensities of 0.05, and 0.5. Fig. 7(d) shows that pratically there are no two separated pulses in time. It is interesting to observe that in this situation the pump [Fig. 7(c)] does not split before the cloning process.
there is still energy available to promote it again and that is why 4p pulses split in two 2p pulses. By varying the relation between the intensities of pump and signal, one may accelerate the cloning process in such a way that it may occur after the breakup as we show in Fig. 7 where the propagation of the pump pulse as well as the signal is illustrated during the first z0 for ratio intensities of 0.05, and 0.5. Fig. 7(d) shows that pratically there are no two separated pulses in time. It is interesting to observe that in this situation the pump [Fig. 7(c)] does not split before the cloning process.
3.3. SOLITION INTERACTIONS
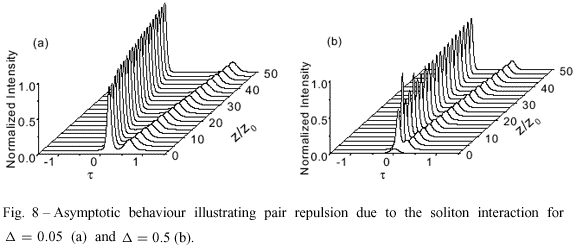
We now turn to long propagation distances, after the pump pulse is depleted. This asymptotic behaviour, is illustrated in Fig. (8) where one can clearly see a repulsive interaction between the pair. At this propagation distance, the pump is already fully depleted and the population is trapped in level  3
3 . Therefore the coupled set of equations
. Therefore the coupled set of equations  4
4 -
-  6
6 ,(9) and (10) is reduced to one single ordinary nonlinear Schrödinger equation for the amplified signal whose initial condition is given by a two-soliton solution. The properties of such solitons, were defined in the beginning of the propagation by the pump and signal interaction from which the soliton pair was originated. We can see that the taller pulse moves forward with respect to the time coordinate frame employed here while the smaller one suffers a delay. This means that the taller soliton goes faster than the group velocity and gets ahead of the smaller one which propagates with a velocity smaller than the group velocity. According to analytical, experimental and numerical work on soliton interactions (Gordon 1983, Aitchison et al. 1991, Hermansson and Yevick 1983), the nature of the interaction should be determined by the phase difference
,(9) and (10) is reduced to one single ordinary nonlinear Schrödinger equation for the amplified signal whose initial condition is given by a two-soliton solution. The properties of such solitons, were defined in the beginning of the propagation by the pump and signal interaction from which the soliton pair was originated. We can see that the taller pulse moves forward with respect to the time coordinate frame employed here while the smaller one suffers a delay. This means that the taller soliton goes faster than the group velocity and gets ahead of the smaller one which propagates with a velocity smaller than the group velocity. According to analytical, experimental and numerical work on soliton interactions (Gordon 1983, Aitchison et al. 1991, Hermansson and Yevick 1983), the nature of the interaction should be determined by the phase difference  between the pair and a repulsive interaction should develop for
between the pair and a repulsive interaction should develop for  <
<  < p making the pulses to separate monotonously. Using a variational approach (Anderson and Lisak 1985), one may show that the phase difference between the pair is proportional to the difference between their squared amplitudes, that is,
< p making the pulses to separate monotonously. Using a variational approach (Anderson and Lisak 1985), one may show that the phase difference between the pair is proportional to the difference between their squared amplitudes, that is,  =
=  z(
z( A1
A1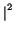 -
- 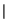 A2
A2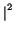 ). By varying the ratio of the pump intensity relative to the signal intensity one may change the relative amplitudes of the resulting pair, controlling the phase difference between them and with it, the nature of the soliton interaction as we show in Fig. 8, for
). By varying the ratio of the pump intensity relative to the signal intensity one may change the relative amplitudes of the resulting pair, controlling the phase difference between them and with it, the nature of the soliton interaction as we show in Fig. 8, for 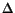 = 0.05 (Fig. 8a) and
= 0.05 (Fig. 8a) and 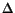 = 0.5 (Fig. 8b). These graphs show clearly that by increasing
= 0.5 (Fig. 8b). These graphs show clearly that by increasing 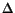 , the interaction between the two soliton pulses is weakened. Another parameter that influences the asymptotic soliton interaction is the initial overlap between A12 and A13 as we show in Fig. 9, where we plot the asymptotic behaviour of the soliton pair for
, the interaction between the two soliton pulses is weakened. Another parameter that influences the asymptotic soliton interaction is the initial overlap between A12 and A13 as we show in Fig. 9, where we plot the asymptotic behaviour of the soliton pair for 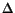 = 0.3. Comparing Fig. 9a (total overlap) with Fig. 9b (partial overlap according to the inset) we notice that as the overlap decreases the interaction is modified from the repulsive behavior. In fact we see one soliton crossing the other in a kind of an intermingled state.
= 0.3. Comparing Fig. 9a (total overlap) with Fig. 9b (partial overlap according to the inset) we notice that as the overlap decreases the interaction is modified from the repulsive behavior. In fact we see one soliton crossing the other in a kind of an intermingled state.
4. CONCLUSIONS
In conclusion, we have studied the simultaneous propagation of a pair of optical pulses through a doped optical fiber, taking into account the resonances provided by the impurities by modelling these after a three-level system. We have found through numerical simulations the cloning of mixed SIT-NLS solitons simultaneous with the transfer of the population until the atomic system evolves into a population trapped state. In the case of high order 4p solitons we have found breaking up and cloning processes that are controlled by the initial relative intensities and overlaps of the pump and signal pulses at the beginning of the whole process. In contrast with results in the literature, we have shown that the pair resulting from the breaking up are not separate but rather interact just like a two-soliton solution. Furthermore, we have demonstrated that the nature of this interaction may be controlled by varying the initial intensity ratio and overlap between pump and signal from which the pair has originated.
The investigation presented here shows remarkable properties of CPT states of atoms interacting with pulses propagating in fibers, that can be used in optical based communication systems. As an example, the effect of soliton cloning in doped fibers may be used to generate solitons streams at different wavelengths with potential applications in soliton multiplexing.
ACKNOWLEDGMENTS
This work was partially supported by the Brazilian agencies: FINEP, CNPq, CAPES and FAPEAL.
RESUMO
Investiga-se numericamente a propagação simultânea de dois pulsos ópticos através de um meio dispersivo não linear dopado, modelado por um sistema ressonante de três níveis, usando-se uma abordagem de equações generalizadas não lineares de Schrödinger. Estas últimas incluem a contribuição das ressonâncias do dopante cuja dinâmica é regida pelas equações de Bloch. Neste trabalho, revemos as possibilidades interessantes que a combinação de efeitos dispersivos não lineares com o aprisionamento coerente da população oferecem, tais como: clonagem, quebra e interação entre solitons.
Palavras-chave: soliton, coerência quântica, não-linearidade, clonagem.
FONSECA EJS, CAVALCANTI SB AND HICKMANN JM. 2001. Soliton interaction in a nonlinear waveguide in the presence of resonances. Phys. Rev E., in press.
- AGRAWAL GP. 1992. Fiber-Optics Communication Systems John Wiley. New York.
- AITCHISON JS, WEINER AM, SILBERBERG Y, LEAIRD DE, OLIVER MK, JACKEL JL AND SMITH PWE. 1991. Experimental observetion of spatial soliton interactions. Opt. Lett. 16: 15-18.
- ALZETTA G, GOZZINI A, MOI L AND ORRIOLS G. 1976. Experimental method for observation of RF transitions and laser beat resonances in oriented Na vapor. Nuovo Cimento B 36: 5-20.
- ANDERSON D AND LISAK M. 1985. Bandwidth limits due to mutual pulse interaction in optical soliton communication systems. Opt. Lett. 11: 174-176.
- CAETANO DP, CAVALCANTI SB, DE SOUZA RF AND HICKMANN JM. 1998. Soliton cloning in a dispersive nonlinear medium coherently driven. Paper Tu. Nonlinear Optics: Materials, Fundamentals and Applications (Princeville, Hawaii, 1998), paper MC32, pp. 119-21.
- CAETANO DP, FREITAS JFL, CAVALCANTI SB AND HICKMANN JM. 2000. Parametric amplification and break-up of a high order soliton in a nonlinear coherent driven medium. Nonlinear Optics: Materials, Fundamentals and Applications (Lihue, Hawaii, 2000), paper TuB8, pp. 77-9.
- EBERLY JH. 1995. Transmission of dressed fields in three-level media. Quantum Semiclassical Optics 7: 373-384, and references therein.
- GARDNER CS, GREENE JM, KRUSKAL MD AND MIURA RM. 1967. Method for solving Korteweg-Devries equation. Phys Rev Lett 19: 1095-1098.
- GORDON JP. 1983. Interaction forces among solitons in optical fibers. Opt Lett 8: 596-598.
- HARRIS SE. 1997. Electromagnetically induced transparency. Phys Today 50: 36-42.
- HAU LV, HARRIS SE, DUTTON Z AND BEHROOZI CH. 1999. Light speed reduction to 17 meters per second in an ultracold atomic gas. Nature 397: 594-598.
- HERMANSSON B AND YEVICK D. 1983. Numerical Investigation of Soliton Interaction. Electron Lett 19: 570-571.
- LAMB JR. GL. 1971. Analytical description of ultrashort optical pulse propagation in a resonant medium. Rev Mod Phys 43: 99-123.
- LIU C, DUTTON Z, BEHROOZI CH AND HAU LV. 2001. Observation of coherent optical information storage in an atomic medium using halted light pulses. Nature 409: 490-493.
- MAIMISTOV AI AND MANYKIN EA. 1983. Propagation of ultrashort optical pulses in resonant nos-linear light guides. Zh. Eksp. Teor. Fiz. 85: 1177 [Sov. Phys. JETP 58: 685-688.]
- MCCALL SL AND HAHN EL. 1969. Self induced transparency. Phys Rev 183: 457-485.
- NAKAZAWA M, YAMADA E AND KUBOTA H. 1991a. Coexistence of Self-Induced Transparency Soliton and Nonlinear Schrödinger Soliton. Phys Rev Lett 66: 2625-2628.
- NAKAZAWA M, KIMURA Y, KUROKAWA K AND SUZUKI K. 1991b. Self-induced-transparency solitons in an erbium-doped fiber waveguide. Phys Rev A 45: R23-R26.
- NAKAZAWA M, SUZUKI K, KIMURA Y AND KUBOTA H. 1991c. Coherent p-pulse propagation with pulse breakup in an erbium-doped fiber waveguide amplifier. Phys Rev A 45: R2682-2685.
- VEMURI G, AGARWAL GS AND VASAVADA KV. 1997. Cloning, Dragging, and Parametric Amplification of Solitons in a Coherently Driven, Nonabsorbing System. Phys Rev Lett 79: 3889-3892.
Publication Dates
-
Publication in this collection
08 June 2001 -
Date of issue
June 2001
History
-
Accepted
30 Mar 2001 -
Received
23 Mar 2001