Automorphisms and non-integrability

MATHEMATICAL SCIENCES

Automorphisms and non-integrability

Jorge V. Pereira; Percy F. Sánchez

Instituto de Matemática Pura e Aplicada, Estrada D. Castorina, 110, 22460-320 Rio de Janeiro, RJ, Brasil

^{Correspondence}

ABSTRACT

On this note we prove that a holomorphic foliation of the projective plane with rich, but finite, automorphism group does not have invariant algebraic curves.

Key words: Holomorphic Foliations, Jouanolou Theorem.

RESUMO

Seja {\mathcal F} uma folheação do plano projetivo complexo de grau d com grupo de automorfismo finito e cuja ação no espaço de cofatores não possui ponto fixo. Neste artigo mostramos que se {\mathcal F} possui ao menos uma singularidade genérica então {\mathcal F} não possui nenhuma curva algébrica invariante.

Palavras-chave: Folheações Holomorfas, Teorema de Jouanolou.

1 INTRODUCTION

On the monograph (Jouanolou 1979) it is proved that for every d > 2, there exists a residual subset of the space of degree d holomorphic foliations of the projective plane whose elements do not have any invariant algebraic curve. The hard part of the proof is to exhibit an explicit example having such property. Jouanolou shows that the foliations induced by the homogeneous 1-forms

where d > 2, have such properties. His proof explores the richness of the automorphism groups of such examples.

In (Zoladek 1998) new examples of foliations of the projective plane without invariant algebraic curves are constructed. These examples also have rich automorphism groups.

In (Maciejewski et al. 2000), the four authors prove that some higher dimensional analogues of Jouanolou's examples do not have invariant algebraic hypersurfaces. Again the automorphism group of these foliations play a major role on the course of the proof.

Besides taking advantage of a rich automorphism group the above mentioned works make use of the explicit form of the equations investigated and impose some restrictions on the singularities of the equations.

The purpose of this note is to settle a general result for foliations of the projective plane with rich automorphism group. Unfortunately we cannot completely get ride of the hypothesis on the singular set of the foliation, although our assumptions are on the eigenvalues of just one of the singularities. More precisely we prove the following

THEOREM 1. Let

be a holomorphic foliations foliations of

². Suppose that

has at least one singularity with non-singular linear part and whose quotient of eigenvalues is not rational nor a root of a unity. If the automorphism group of

is finite and acts without nontrivial fixed points on the space of cofactors then

does not admit any invariant algebraic curve.

For a definition of the space of cofactors and the action of automorphism group of the foliation on it the reader should consult section 2.

2 COFACTOR REPRESENTATION

On this paper a degree d singular holomorphic foliation of ² will be given by a 1-form w on ³ annihilated by the radial vector field with homogeneous coefficients of degree d + 1. More explicitly if w = Adx + Bdy + Cdz then A, B and C are homogenous polynomials of degree d + 1 and x A + yB + zC = 0. We will denote the foliation induced by w by 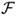_w.

The automorphism group of w is the subgroup of SL(3, ³) defined by

The automorphism group of 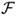_w is the image of Aut(w) by the natural projection SL(3, ) ® PSL(3, ), i.e., Aut(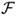_w) = P(Aut(w)).

Note that if f Î Aut(w) then there exists a non zero complex number l(f) such that f^*w = l(f) · w. Moreover,

is a homomorphism of groups.

If F Î [x, y, z] is a homogeneous polynomial describing an invariant algebraic curve for 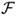then

where Q_F is a 3-form satisfying the following

LEMMA 1. There exists a unique 3-form b_F such that

PROOF. Applying i_R to both sides of d F Ù w = FQ_F we have

It follows from Euler's formula that i_R(dw) = (d + 2)w and consequently

The existence and uniqueness of b_F follow from the De Rham's division Theorem.

From the above Lemma it follows that for every automorphism f of w the following identity holds

If 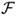is a foliation of degree d then b_F has degree d - 1. Denote by the space of homogeneous 3-forms on ³ of degree d - 1. Hence we have a representation F_w : Aut(w) ® Hom(, ) defined by

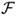Since F_w(µ · Id) = Id for every µ Î ^*, it follows that F_w = o p where p : Aut(w) ® Aut(_w) is the natural projection and

is, by definition, the cofactor representation. We will say that the automorphism group of

acts without nontrivial fixed points on the space of cofactors if

PROPOSITION 1. Let

be a foliation on

². If the automorphism group of

is finite and acts without nontrivial fixed points on the space of cofactors then either

admits liouvillian first integral or

does not admit an invariant algebraic curve.

PROOF. Suppose that 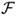admits an invariant algebraic curve C given by homogeneous polynomial F. If we consider the homogeneous polynomial

we see that G is invariant by both 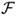and Aut(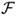). Consequently the cofactor associated to G is a fixed point for and therefore, by hypothesis, is equal to zero. Consequently, it follows from Lemma 1 that

To conclude one has to observe that the multivalued 1-form · w is closed and induces a closed multivalued one-form on the projective plane. In particular 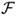admits a liouvillian first integral.

EXAMPLE 1. Let H be the subgroup of Aut(²) generated by f₁[x : y : z] = [-x :- y : z] and f₂[x : y : z] = [-x : y : -z]. Among the degree 2 foliations invariant by G there exists a ²Ì Fol(2) = H⁰(², W¹(4)) whose elements are induced by the 1-forms

The cofactor representation is given by

In particular H acts without nontrivial fixed points. The lines {ay² + bz² = 0} and {-ax² -cz² = 0} are invariant by both 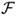_(a,b,c) and Aut(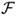_a,b,c). Consequently

and

_(a,b,c) has a liouvillian first integral as predicted by Proposition 1. In fact one can easily verify that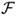 _(a,b,c) has a rational first integral.

3 PROOF OF THE MAIN RESULT

Before starting the proof of the main result let us state a simple lemma

LEMMA 2. Let X be a holomorphic vector field on a neighborhood of 0 Î and w = i_Xdx Ùdy a 1-form dual to X. Assume that 0 is a singularity of X. If there exists a 1-form h such that dw = h Ù w then the trace of DX(0) is zero.

PROOF. Since w = i_Xdx Ù dy we have dw = div(X) dx Ù dy = (Tr(DX(0)) + h.t.o)dx Ù dy. Now as 0 is a singularity of X we have:

Let p be the reduced singularity of 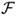whose quotient of eigenvalues is not rational nor a root of unity. If 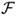admits an invariant algebraic curve C we can suppose without loss of generality that C is reduced and invariant by Aut(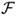). Moreover we can also assume that Aut(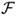) acts transitively on the set of irreducible components of C.

It follows from Lemma 1 that

where F is a reduced homogeneous polynomial defining C.

From Lemma 2 we have p Î C. Since p is reduced, we can choose local coordinates (x, y) where p = (0, 0) and 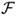is defined in these coordinates by

Suppose that C is smooth at p and locally defined by either {x = 0} or {y = 0}. From (1) and (2) we obtain in both cases that l is rational contradicting our hypothesis. Therefore C will have two branches passing through p. In this case

Comparing this last equality with (1) we deduce that d + 2 = deg(F) and that the foliation is given by the closed 1-form with simple poles along C. By Theorem 2.1 of (Cerveau and Mattei 1982) it follows that 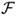is defined by a closed meromorphic 1-form

where F_i are the irreducible factors of F, F = F₁F₂...F_k. Writing the closed 1-form above in local coordinates (x, y) this implies that x and y divide locally two distinct polynomials F_i, since otherwise the quotient of eigenvalues at p would be 1.

Without loss of generality we may suppose that x divides F₁ and y divides F₂. Thus we obtain that

Consequently we have l = .

We can suppose without loss of generality that there exists f Î Aut(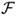) such that . Applying f to we see that there exists a root of unity b such that

Comparing the coefficients of in both sides of the equation we infer that a₁ = ba₂. Therefore l = -b^-1 contrary to our hypothesis.

4 SOME EXAMPLES

4.1 THE EXAMPLES OF JOUANOLOU

As stated in the introduction the examples of Jouanolou are the foliations of

² induced by the 1-forms w_d = i_Ri_Xddx Ù dy Ù dz, where d > 2 and X_d =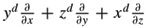 . We will denote the foliation induced by w_d by 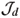. The automorphisms group of 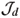is isomorphic to the semidirect product of 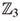and 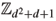In particular it has order 3 · (d² + d + 1). It is generated by f₁[x : y : z] = [z : x : y] and f₂[x : y : z] = [dx : d^d y : d^d2] where d is a d² + d + 1-root of the unity.

The cofactor representation is given by

LEMMA 3. If d 1 mod 3 then the automorphism group of

acts without nontrivial fixed points on the space of cofactors.

PROOF. The eigenvalue of F_d(f₂) : corresponding to the eigenvector xⁱ y^j z^k dx Ù dy Ù dz, i + j + k = d - 1, is given by . To prove the lemma it is sufficient to show that for d 1 mod 3 the system

has no solutions with i, j and k nonnegative integers.

Subtracting the first equation from the second we obtain that

Since d²+ d + 1 = (d + 2)(d - 1) +3 we see that the greatest common divisor of d² + d + 1 and d - 1 is 1 whenever d 1 mod 3. Therefore from our assumptions we have that

and j, k > 0 implies that j + (d + 1)k > d² + d.

Since j, k < d - 1 we obtain that j +(d + 1)k < d² + d - 2. This contradiction is sufficient to settle the lemma.

From the lemma above and Theorem 1 we obtain a proof that 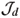has non algebraic solutions when d ¹ 1 mod 3. Note that this result also holds for every integer d greater than or equal to 2, see (Jouanolou 1979).

4.2 ONE OF ZOLADEK'S EXAMPLES

Denote by , [a : b : c] Î ², the degree 3 foliations of ² defined by the 1-forms

These foliations are invariant by the automorphism

where, d is the seventh root of unity.

A simple computation shows that A acts without non-trivial fixed points in .

When a · b · c ¹ 0, the singularities distinct from {[0 : 0 : 1],[0 : 1 : 0],[1 : 0 : 0]} have as quotient of eigenvalues . Therefore from Theorem 1 the foliation has no algebraic solutions when a · b · c ¹ 0.

ACKNOWLEDGMENTS

Jorge Vitório Pereira is supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico (PROFIX-CNPq).

Manuscript received on November 19, 2004; accepted for publication on March 25, 2005; presented by MANFREDO DO CARMO

• CERVEAU D AND MATTEI J-F. 1982. Formes intégrables holomorphes singulières, Astérisque 97, SMF.
• JOUANOLOU J-P. 1979. Equations of Pfaff algébriques, Lect Notes in Math 708, Springer Verlag, Berlin.
• MACIEJEWSKI A, OLLAGNIER J, NOWWICKI A AND STRELCYN J-M. 2000. Around Jouanolou non-integrability theorem. Indag Mathem 11: 239-254.
• ZOLADEK H. 1998. New examples of holomorphic foliations without algebraic leaves. Stud Math 131: 137-142.

Publication Dates

• Publication in this collection
  24 Aug 2005
• Date of issue
  Sept 2005

History

• Accepted
  25 Mar 2005
• Received
  19 Nov 2004