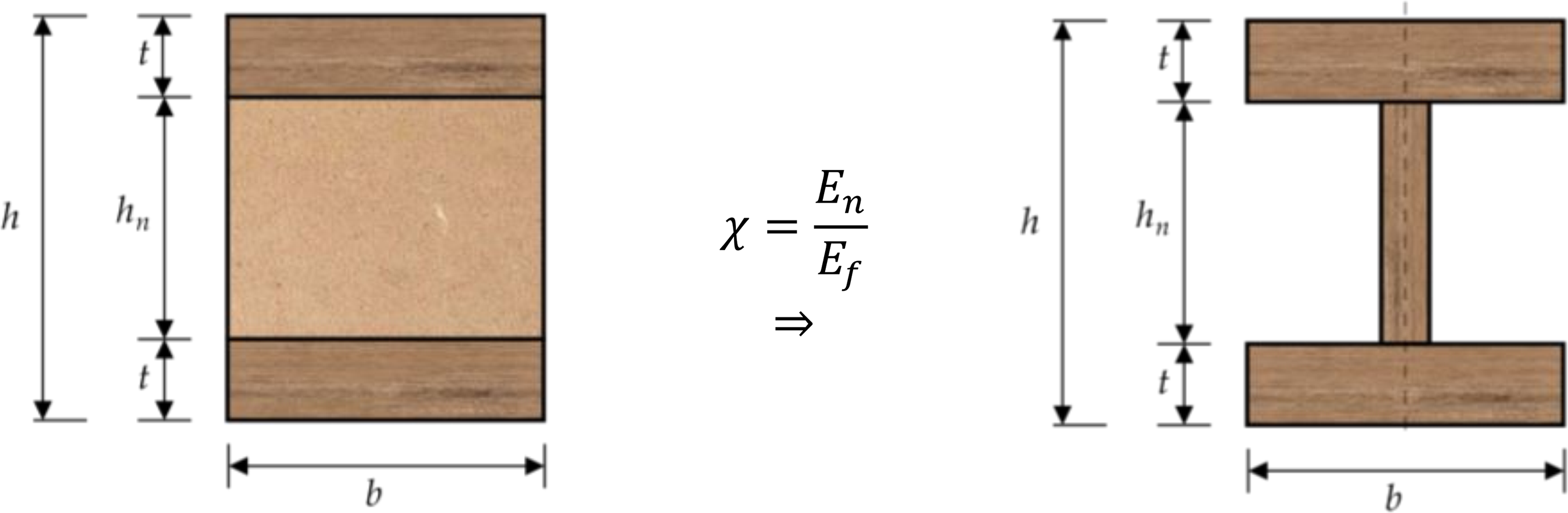Análise estatística da rigidez de vigas de MLC confeccionadas com madeiras de pinus coladas com a resina RS 216-M baseada na ABNT NBR 7190-1:2022

Statistical analysis of the stiffness of glulam beams made with pinus wood bonded with RS 216-M resin based on ABNT NBR 7190-1:2022

Resumos

Este artigo examina a rigidez à flexão (EI) de vigas de madeira lamelada colada (MLC) de Pinus, utilizando equação analítica, testes experimentais e simulação numérica para validar as formulações da norma NBR 7190-1 (ABNT, 2022a). O estudo foi conduzido com madeira Pinus C30, com lamela unidas por adesivo resorcinol formol. Os testes realizados compararam as estimativas de rigidez à flexão derivadas de equação analítica proposta pela referida norma e de simulação numérica no software ANSYS com dados experimentais, aplicando o teste de Tukey para determinar a significância estatística das diferenças. Os resultados mostraram que tanto a verificação analítica quanto as simulações numéricas ofereceram previsões próximas aos valores experimentais, com discrepâncias menores que 10% em termos de erro percentual absoluto médio, validando assim a eficácia das formulações normativas para o dimensionamento de vigas de MLC. O estudo confirmou a adequação da madeira de Pinus para uso em aplicações estruturais na construção civil.

Palavras-chave
Madeira lamelada colada (MLC); Espécie Pinus ; Rigidez a flexão; modelos analíticos; Método dos elementos finitos

This article examines the bending stiffness (EI) of glued laminated timber (glulam) beams made of Pinus wood, using analytical modeling, experimental test and numerical simulation to validate the formulations of the Brazilian standard NBR 7190-1 (ABNT, 2022a). The study was conducted with Pinus C30 wood, with lamella bonded by resorcinol-formaldehyde adhesive. The tests compared the bending stiffness estimates derived from analytical equation and proposed by the aforementioned standard and numerical simulations in the ANSYS software with experimental data, applying the Tukey test to determine the statistical significance of the differences. The results showed that both analytical verification and numerical simulations provided predictions close to experimental values, with discrepancies less than 10% in terms of mean absolute percentage error, thus validating the effectiveness of normative formulations for the design of glulam beams. The study confirmed the suitability of Pinus wood for use in structural applications in civil construction.

Keywords
Glued-laminated timber (Glulam); Pinus specie; Bending stiffness; Analytical models; Finite element method

Introdução

A madeira destaca-se no setor de construção civil não só por ser um recurso natural abundante, eficiente e sustentável, oferecendo excelente relação entre resistência mecânica e densidade. Estudos como Namari et al. (2021), evidenciam propriedades superiores da madeira comprimida em relação a materiais como aço e concreto, destacando sua eficiência energética. Além disso, a madeira possui baixa condutividade térmica, contribuindo para o isolamento térmico e segurança em edificações (Chen et al., 2020).

Essas características, combinadas com a tenacidade inerente da madeira, tornam-na uma escolha robusta e resiliente. A madeira de Pinus, proveniente de reflorestamentos, apresenta vantagens como adaptabilidade, rápido crescimento e sustentabilidade. Estudos indicam seu uso eficaz na recuperação de ecossistemas degradados e na produção de madeira para aplicações estruturais (Adamopoulos; Wimmer; Milios, 2012; Adili; El Aouni; Balandier, 2013; Espelta; Retana; Habrouk, 2003). Essas práticas reforçam a importância dos pinheiros na conservação e gestão florestal sustentável.

Nos países desenvolvidos da Europa e América do Norte, a caracterização e promoção do uso da madeira em diversas aplicações têm sido intensivas nas últimas décadas, aproveitando-se das vantagens oferecidas pelo material. No entanto, no Brasil, o uso da madeira desde a década de 70 foi realizado sem o devido acompanhamento técnico. A norma brasileira de madeira NBR 7190 foi estabelecida apenas em 1997, com uma revisão subsequente em 2022. Adicionalmente, os significativos investimentos em pesquisa nas indústrias de aço e concreto contribuíram para que a adoção destes materiais na construção civil brasileira superasse a da indústria madeireira (Molina, 2017).

Neste contexto, o sistema construtivo em madeira laminada colada (MLC) surge como uma alternativa sustentável na construção civil, uma vez que permite o uso de madeiras de reflorestamento para a edificação de grandes estruturas. Apesar de suas vantagens, este sistema ainda não é amplamente adotado no mercado brasileiro, devido ao número limitado de indústrias produtoras de MLC no país. No entanto, os estudos sobre essa técnica estão aumentando, o que ajuda a fomentar a disseminação de informações e promover a aceitação deste produto no mercado brasileiro (Teles et al., 2010).

De modo geral, a MLC é um sistema industrializado no qual as lamelas de madeira são unidas com adesivo, permitindo a criação de grandes elementos estruturais. Este sistema construtivo viabiliza a execução de projetos arquitetônicos distintos, pois os elementos de MLC podem ser fabricados em formas curvas, grandes dimensões e são capazes de suportar extensos vãos livres.

A MLC oferece flexibilidade de design, maior controle de qualidade e menor impacto ambiental (Balasbaneh; Sher, 2021; Yadav; Kumar, 2022). A organização estratégica das lamelas, como destacado por Mallo e Espinoza (2015), otimiza a resistência e a estabilidade estrutural, alinhando benefícios econômicos e ambientais.

Na fabricação da MLC, a disposição estratégica das lamelas é essencial para a obtenção de elementos estruturais com maior rigidez e resistência. Devido à variação do módulo de elasticidade entre as lamelas e sua posição ao longo da altura da seção transversal, é crucial utilizar modelos de cálculo específicos. Estes modelos ajudam a estimar a rigidez à flexão, a carga última, e a analisar possíveis modos de falha, fundamentais para o dimensionamento estrutural correto.

A pesquisa avançada envolvendo o estudo das propriedades mecânicas da MLC sugere a necessidade de uma abordagem em escala real para capturar as características efetivas de cada material em diferentes escalas estruturais (Flores et al., 2016). Adicionalmente, modelos específicos para a análise de deformações em elementos estruturais curvos de madeira lamelada também são discutidos, ressaltando a influência do tipo de madeira e do tempo sobre as deformações (Altınok; Burdurlu; Özkaya, 2008).

Além disso, para o projeto contra incêndios, modelos de cálculo para a taxa de carbonização de elementos estruturais de madeira, incluindo madeira lamelada pregada e colada, foram avaliados e comparados com resultados de testes, sublinhando a precisão e aplicabilidade dos modelos (Friquin, 2010).

A abordagem e especificações acerca de características das MLC, tais como espessuras das lamelas, métodos de ensaio, premissas e métodos de cálculo, entre outras, são estabelecidas por documentos normativos diversos. No Brasil, o projeto de estruturas de madeira é regulamentado pela norma NBR 7190-1 (ABNT, 2022a) que propõe um modelo de cálculo (método da seção transformada) baseado na rigidez (EI) do elemento fletido de MLC.

Referencial teórico

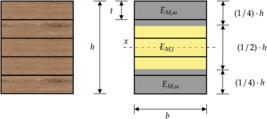
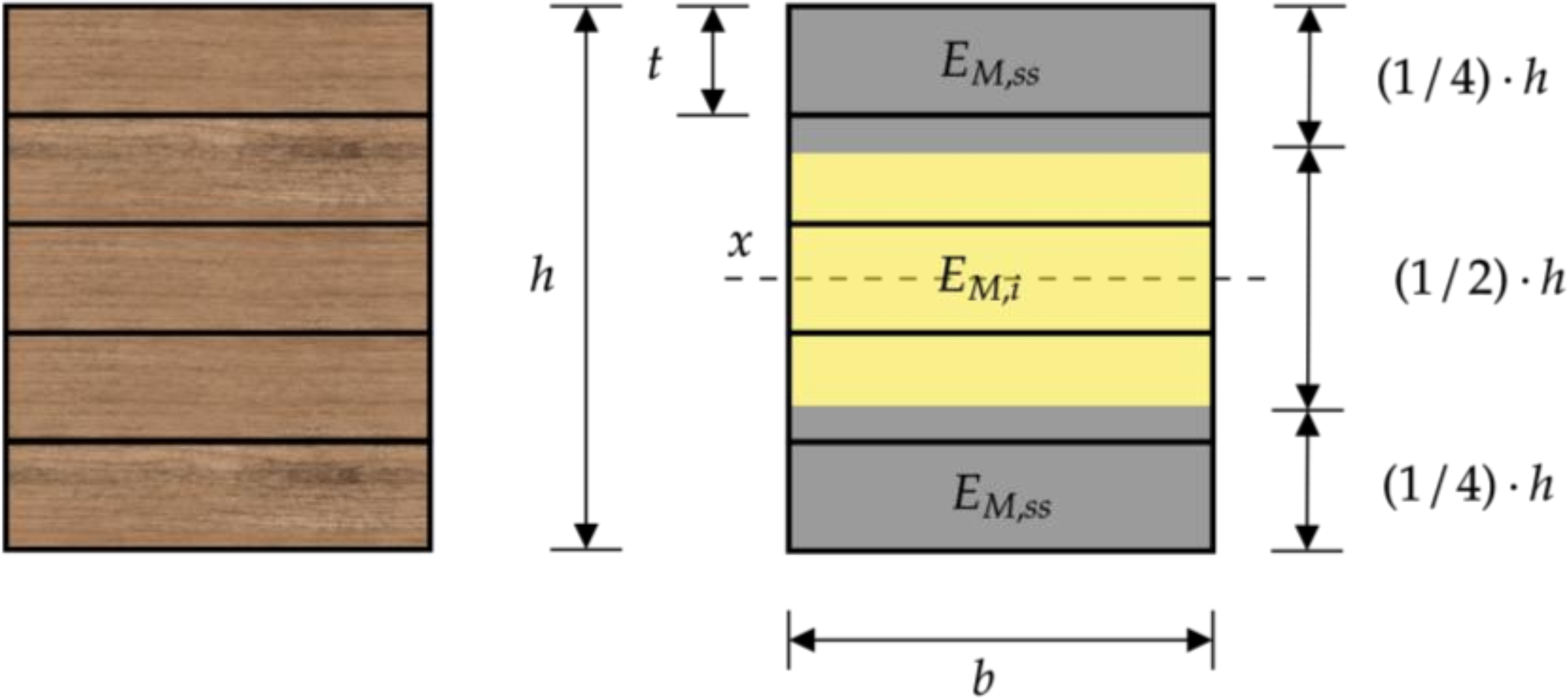
A norma NBR 7190-1 (ABNT, 2022a) considera o cálculo de rigidez à flexão (E · I) a partir da Equação 1, que contabiliza o valor médio dos módulos de elasticidade do conjunto das lamelas que compõe as faces (f) superior e inferior (E_M,ss) assim como a média dos valores dos módulos de elasticidade das demais lamelas (E_M,i) que compõe a seção transversal (núcleo - n), sendo o momento de inércia do núcleo e I_(1/4) o momento de inércia das faces (Figura 1), tal como apresentado nas e Equações 2 e 3. Este cálculo é fundamentado no Teorema dos Eixos Paralelos, que permite determinar o momento de inércia de uma seção composta considerando a distância entre o eixo neutro da seção completa e os eixos centrais das subáreas individuais. Quando o eixo central do retângulo coincide com o eixo neutro da seção, o cálculo pode ser simplificado, eliminando a necessidade de ajuste para a posição relativa entre os eixos.

$E\cdot I=2\cdot E_{M,ss}\cdot I_{(1/4)}+E_{M,i}\cdot I_{(1/2)}$ (Eq. 1)

$I_{(1/4)}=\frac{b\cdot {\left(\frac{h}{4}\right)}^3}{12}+\left(b\cdot \frac{h}{4}\right)\cdot {\left(\frac{\frac{h}{2}}{2}+\frac{\frac{h}{4}}{2}\right)}^2$ (Eq. 2)

$I_{(1/4)}=\frac{b\cdot {\left(\frac{h}{4}\right)}^3}{12}+\left(b\cdot \frac{h}{4}\right)\cdot {\left(\frac{\frac{h}{2}}{2}+\frac{\frac{h}{4}}{2}\right)}^2{I}_{(1/2)}=\frac{b\cdot {\left(\frac{h}{2}\right)}^3}{12}$ (Eq. 3)

Considerando $\chi =E_n/E_f$ como um parâmetro adimensional, e com a seção transversal de uma viga de MLC sendo retangular, a norma nacional propõe a Equação 4 para estimar EI, obtida por meio da simplificação das Equações 2 e 3, e posterior substituição na Equação 1, conforme representado abaixo. Nesta equação, E_M,i representa o módulo de elasticidade do núcleo (E_n) e E_M,ss é o módulo de elasticidade das faces (E_f). Resultando na rigidez à flexão (E · I) tal como apresentado nas Equações 5, 6, 7, 8, 9 e 10.

$I_{\left(\frac{1}{4}\right)}=\frac{b\cdot {\left(\frac{h}{4}\right)}^3}{12}+\left(b\cdot \frac{h}{4}\right)\cdot {\left(\frac{\frac{h}{2}}{2}+\frac{\frac{h}{4}}{2}\right)}^2=\frac{b\cdot h^3}{4^3\cdot 12}+\left(b\cdot \frac{h}{4}\right)\cdot {\left(\frac{h}{4}+\frac{h}{8}\right)}^2=\frac{b\cdot h^3}{768}+\left(b\cdot \frac{h}{4}\right)\cdot {\left(\frac{3}{8}h\right)}^2=\frac{b\cdot h^3}{768}+\left(b\cdot \frac{h}{4}\right). \left(\frac{9}{64}{h}^2\right)=\frac{b\cdot h^3}{768}+\frac{9\cdot b\cdot h^3}{256}=\frac{7\cdot b\cdot h^3}{192}$ (Eq. 4)

$I_{(1/2)}=\frac{b\cdot {\left(\frac{h}{2}\right)}^3}{12}=\frac{b}{12}\cdot \left(\frac{h^3}{8}\right)=\frac{b\cdot h^3}{96}$ (Eq. 5)

$E\cdot I=2\cdot E_f\cdot I_{(1/4)}+E_n\cdot I_{(1/2)}$ (Eq. 6)

$E\cdot I=2\cdot E_f\cdot \frac{7\cdot b\cdot h^3}{192}+E_n\cdot \frac{b\cdot h^3}{96}$ (Eq. 7)

$E\cdot I=E_f\cdot \frac{7\cdot b\cdot h^3}{96}+E_n\cdot \frac{b\cdot h^3}{96}$ (Eq. 8)

$E\cdot I=\frac{E_f\cdot b\cdot h^3}{96}\left(7+\frac{E_n}{E_f}\right)$ (Eq. 9)

$E\cdot I=\frac{E_f\cdot b\cdot h^3}{96}\cdot (7+\chi )$ (Eq. 10)

Figura 1
Representação esquemática de uma seção transversal de MLC para o uso da Equação (1)

Outra possibilidade para efetuar a estimativa da rigidez a flexão de vigas de MLC é a metodologia proposta por Fiorelli e Dias (2011) consideraram o método da seção transformada na determinação da rigidez a flexão de vigas de MLC reforçadas por compósitos laminados em fibras de vidro. Tal metodologia utilizada pelos autores exige a determinação do centro de gravidade (CG - Equação 11) da seção transversal para posterior obtenção da rigidez a flexão (Equação 12).

$y_{CG}=\underset{i=1}{\overset{N}{\Sigma }} \left[\frac{\frac{E_i}{E_{\mathit{max}}}\cdot b\cdot t_i\cdot \left(\frac{t_i}{2}+t_i\cdot (i-1)\right)}{\underset{i=1}{\overset{N}{\Sigma }} \left(\frac{E_i}{E_{\mathit{max}}}\cdot b\cdot t_i\right)}\right]$ (Eq. 11)

$E\cdot I=\underset{i=1}{\overset{N}{\Sigma }} \left(\frac{E_i\cdot b\cdot t_i^3}{12}+E_i\cdot b\cdot t_i\cdot d_i^2\right)$ (Eq. 12)

Das Equações 11 e 12, N denota o número de lamelas, E_i é o módulo de elasticidade de cada lamela que compõe a seção transversal da viga de MLC, E_max consiste no maior valor do módulo de elasticidade das lamelas, b é a largura da seção transversal, t_i é a espessura de cada lamela e d_i é a distância do centro de gravidade de cada lamela ao centro de gravidade da seção transversal (γ_CG). Ressalta-se que o método da seção transformada também tem sido considerado na estimativa dos valores de rigidez a flexão de vigas de MLC em pesquisas diversas, como nas de Nadir et al. (2016), Soriano, Pelles e Mascia (2016), Gao et al. (2019) e Peixoto et al. (2022).

Conforme estabelecido na norma NBR 7190-1 (ABNT, 2022a), a estimativa da rigidez à flexão de vigas de MLC baseia-se no método da seção transformada em conjunto com a teoria de compósitos do tipo sanduíche. Nestes compósitos, o núcleo, geralmente um material de menor densidade e resistência, atua principalmente para distanciar as faces ou lamelas, que são feitas de um material mais resistente e rígido. Essa configuração aumenta o momento de inércia da seção transversal e, consequentemente, a rigidez à flexão do compósito (Ferdous; Manalo; Aravinthan, 2018; Li; Zhang, 2023).

Na teoria de compósitos estruturais, é possível adaptar diversos modelos teóricos para estimar a rigidez à flexão de vigas de MLC. A aplicação desses modelos permite comparar suas estimativas de rigidez (E · I) com valores obtidos experimentalmente, identificando assim o modelo que oferece a maior precisão.

Levy Neto e Pardini (2016) mostram que se pode calcular o módulo de elasticidade efetivo (E_ef) de um compósito laminado estrutural utilizando a Equação 13. Nesta equação, E_i representa o módulo de elasticidade de cada lamela individual em um total de N lamelas. A equação também considera h, que é a altura total da seção transversal do laminado, e γ_i e γ_i-1, que são as posições das faces de cada lamela em relação ao eixo de simetria da seção. É importante notar que esta equação é válida para laminados simétricos. No caso de compósitos com um número ímpar de lamelas, como as vigas de MLC com 5 lamelas, estudadas nesta pesquisa, a lamela central deve ser considerada como dividida em duas partes. Além disso, para aplicar a Equação 13 em vigas de MLC, os módulos de elasticidade das lamelas que estão a iguais distâncias dos eixos de simetria devem ser tratados como médias dos valores de elasticidade das duas lamelas correspondentes equidistantes do eixo de simetria.

$E_{ef}=\frac{8}{h^3}\cdot \underset{i=1}{\overset{N/2}{\Sigma }} E_i \cdot \left(y_i^3-y_{i-1}^3\right)$ (Eq. 13)

A rigidez à flexão das vigas de MLC é obtida multiplicando-se o valor do módulo de elasticidade efetivo (E_ef – Equação 13) pelo momento de inércia da seção transversal (seção retangular), o que resulta na Equação 14.

$$E\cdot I=\frac{2\cdot b}{3}\cdot \underset{i=1}{\overset{N/2}{\Sigma }} E_{i }\cdot \left(y_i^3-y_{i-1}^3\right)$$ (Eq. 14)

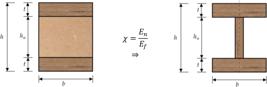
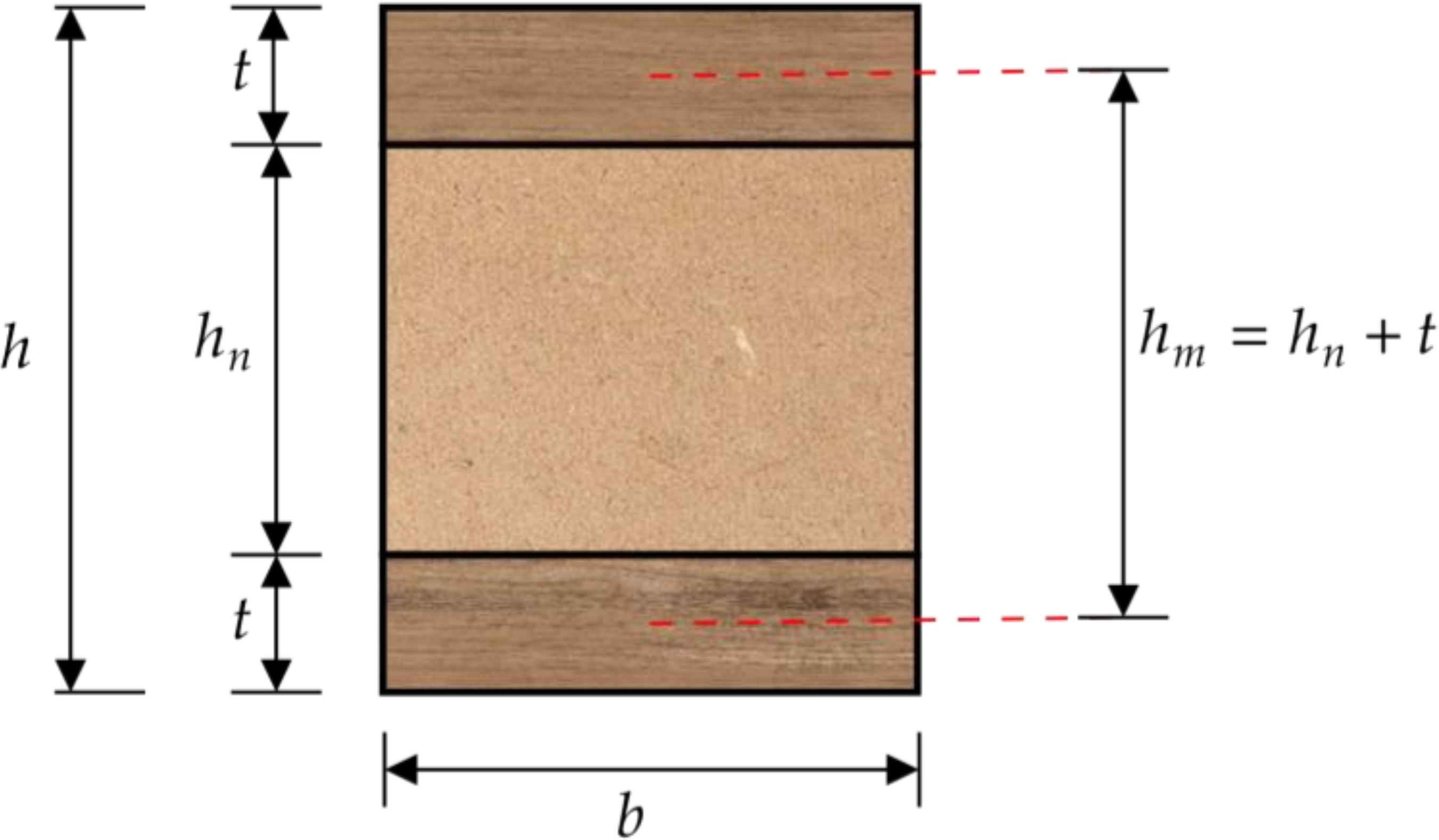
Para o caso de compósitos sanduíche estruturais (Figura 2) e considerando $\chi =E_n/E_f$, a rigidez a flexão resulta na Equações 15 e 16 conforme a norma D7250 (ASTM, 2020). O uso dessa equação adaptada para vigas de MLC exige a consideração do valor médio dos módulos de elasticidade das lamelas centrais e a média dos valores médios dos módulos de elasticidade das lamelas posicionadas nas faces (compósito simétrico).

Figura 2
Seção transversal e identificação dos parâmetros geométricos considerados para o uso da Equação 15

$E\cdot I=\frac{2\cdot b}{3}\cdot \underset{i=1}{\overset{N/2}{\Sigma }} E_i \cdot \left(y_i^3-y_{i-1}^3\right)$ (Eq. 15)

$$E\cdot I=\frac{b\cdot E_f}{12}\cdot \left(2\cdot t^3+6\cdot t\cdot h_m^2+\chi \cdot h_n^3\right)$$ (Eq. 16)

Considerando $\chi =E_n/E_f$, pelo método da seção transformada (Figura 3) aplicado a compósito sanduíche simétrico (Christoforo; Libardi, 2019), a rigidez à flexão resulta na Equação 17. O uso dessa equação para a estimativa da EI em vigas de MLC exige a consideração do valor médio dos módulos de elasticidade das lamelas centrais (que compõe o núcleo) e a média dos valores dos módulos de elasticidade das lamelas posicionadas nas faces (compósito simétrico).

Figura 3
Representação da modificação da seção transversal de uma viga sanduíche pelo método da seção transformada e identificação dos parâmetros geométricos considerados para o uso da Equação 17

$E\cdot I=E_f\cdot \left\{\frac{\chi \cdot b\cdot h_n^3}{12}+2\cdot \left[\frac{b\cdot t^3}{12}+{\left(\frac{h_n}{2}+\frac{t}{2}\right)}^2\cdot b\cdot t\right]\right\}$ (Eq. 17)

Uma alternativa aos modelos analíticos para calcular a rigidez à flexão (e outras variáveis estruturais relevantes) de vigas de MLC é a simulação numérica usando o método dos elementos finitos (MEF). Esse método pode fornecer estimativas de rigidez à flexão (EI) que são mais próximas dos valores obtidos experimentalmente.

Desta forma, a norma brasileira NBR 7190-1 (ABNT, 2022a) apresenta uma fórmula para estimar a rigidez à flexão de vigas de MLC, sendo necessário validar sua precisão por meio de métodos confiáveis. Este estudo tem como objetivo validar a equação de EI para MLC apresentada na NBR 7190-1 (ABNT, 2022a), bem como avaliar outras propostas disponíveis na literatura, utilizando simulação numérica para determinar a rigidez à flexão de vigas MLC de Pinus. Dessa forma, busca-se confirmar a aplicabilidade das equações normativas e a eficácia das abordagens analíticas e numéricas. Considerando a variedade de modelos analíticos e também a aplicação de simulação numérica pelo MEF, este estudo teve como objetivo avaliar a precisão das fórmulas listadas (Equações 10, 12, 14, 16 e 17) e a eficácia da simulação numérica na determinação da rigidez à flexão de vigas MLC de Pinus.

Material e método

Esta seção descreve os materiais e métodos usados nos ensaios experimentais de elementos MLC sob flexão, bem como as técnicas de análise teórica aplicadas aos resultados. As dimensões dos corpos de prova foram escolhidas com base na disponibilidade de equipamentos e espaço no Laboratório de Propriedades dos Materiais da UNESP de Itapeva, sem comprometer a análise dos elementos. Além disso, é importante destacar que a norma NBR 7190-6 (ABNT, 2022c), que aborda métodos de ensaio para madeira lamelada colada estrutural utilizados no presente trabalho.

Nesta pesquisa, foi empregada madeira de reflorestamento Pinus C30, com classes de resistência definidas conforme as diretrizes da norma NBR 7190-1 (ABNT, 2022a). As lamelas de madeira foram coladas utilizando o adesivo resorcinol formol (Cascophen RS-216M).

Caracterização física e mecânica do Pinus

Para o desenvolvimento dos ensaios foram usinadas sete toras de Pinus para produzir lamelas com 50 mm de largura, 15 mm de espessura e 1500 mm de comprimento. A Figura 4 ilustra os corpos de prova extraídos destas toras para o estudo. De cada tora, extraíram-se seis corpos de prova para determinar o teor de umidade, três para ensaios de compressão, três para ensaios de tração e três para ensaios de cisalhamento. Além disso, foi maximizada a quantidade de lamelas retiradas de cada tora para a fabricação dos elementos de MLC. Os resultados dos ensaios de caracterização foram então aplicados às lamelas oriundas da mesma tora. Cabe destacar que, foram extraídos de lotes considerados homogêneos, e as amostras foram devidamente estocadas em local com teor de umidade próximo de 12%.

Figura 4
Representação dos corpos de prova retirados das toras de madeira

Os corpos de prova e as lamelas foram submetidos a um processo de secagem para alcançar um teor de umidade de 12 % ±1. A determinação da umidade das lamelas foi feita conforme a NBR 7190-2 (ABNT, 2022b), calculando-se a partir da massa úmida (m_i) e da massa seca (0%) (m_s) dos corpos de prova. A partir dessas massas, o teor de umidade pode ser obtido com mostrado na Equação 18.

$$U\left(\mathrm{\%}\right)=\frac{m_i-m_s}{m_s}\cdot 100$$ (Eq. 18)

Para determinação da resistência à compressão paralela às fibras, os corpos de prova foram rompidos em uma máquina universal de ensaios (AMSLER - capacidade de carga de 25 toneladas), o teor de umidade (U) dos mesmos no momento dos ensaios foi obtido por meio do medidor de umidade por contato Marrari M5. Com posse do teor de umidade das amostras, os valores de resistência (f_c0) à compressão na direção paralela às fibras foram corrigidos para o teor de umidade de 12% (f_c0,12) com o auxílio da Equação 19, em que f_c0,U consiste na resistência das amostras associadas ao teor de umidade (U).

$U\left(\mathrm{\%}\right)=\frac{m_i-m_s}{m_s}\cdot 100$ (Eq. 19)

Com base nos valores corrigidos da resistência à compressão na direção paralela às fibras (f_c0,12), a Equação 20 foi utilizada para a determinação do valor característico (f_c0,k) para a categorização da madeira nas classes de resistência, em que f₁,f₂ a f_n denotam os valores da resistência à compressão (f_c0,12) em ordem crescente dos n corpos de prova testados (n = 3 por tora, 21 amostras totais).

$f_{c0,k}=max\left\{\begin{array}{c}{f}_1\\ 0.7\cdot \frac{\underset{i=1}{\overset{n}{\Sigma }} f_i}{n}\\ 1.1\cdot \left[2\cdot \left(\frac{f_1+f_2+f_3+\cdots +{\displaystyle \frac{f_n}{2}}-1}{\frac{n}{2}-1}\right)-\frac{f_n}{2}\right]\end{array}\right.$ (20)

É importante mencionar, que a rigidez à flexão E · I de cada lamela foi determinada de maneira não destrutiva, utilizando um ensaio de flexão a três pontos, conforme a Equação 21. Este método é recomendado pela NBR 7190-1 (ABNT, 2022a) para avaliar o módulo de elasticidade em corpos de prova de pequenas dimensões que estejam livres de defeitos. Considerando o ponto da fase linear do diagrama força-deslocamento onde a rigidez à flexão para o cálculo. Além disso, o deslocamento máximo foi limitado a L/200, servindo como um limite de referência para os ensaios.

$E\cdot I=\frac{P\cdot L^3}{48\cdot \delta }$ (Eq. 21)

Para determinar o módulo de elasticidade das lamelas (E_M) foi determinado por meio de ensaios realizados em uma máquina universal de ensaios EMIC (DL-30000), conforme ilustrado na Figura 5. Utilizando um carregamento constante com capacidade de atingir até 300 kN. Entretanto, o valor da força utilizada na Equação 21 foi proveniente de um deslocamento limitado a L/200, que corresponde ao trecho linear da curva tensão × deformação. As lamelas passaram por ensaios de flexão não destrutivos. Esses testes envolviam medir a flecha no meio do vão (δ) correspondente à força (P) aplicada pela máquina de ensaios universal, a distância entre apoios (L) e o momento de inércia da lamela (I), para calcular o módulo de elasticidade, tal como descrito na Equação 22, resultante da manipulação da Equação 21.

Figura 5
Ensaio para obtenção de E_M das lamelas de pinus

$E_M=\frac{P\cdot L^3}{48\cdot \delta \cdot I}$ (Eq. 22)

Processo fabricação da Madeiral Lamelada Colada (MLC)

Para caracterizar as lamelas de madeira dos elementos fletidos, realizaram-se ensaios em corpos de prova extraídos do mesmo lote de madeira das quais as lamelas foram originadas. Nesses testes, foram avaliadas a compressão, a tração e o cisalhamento, todos paralelos às fibras, conforme as recomendações da NBR 7190-2 (ABNT, 2022b).

Para a colagem das lamelas, utilizou-se o adesivo Cascophen RS-216M, acompanhado de um catalisador em pó, na proporção de 10:2 de adesivo para catalisador. Conforme descrito por Cunha (2007), o Cascophen RD—216M é um adesivo à base de resorcinol formol, dissolvido em álcool e água. A aplicação do adesivo foi realizada em ambas as superfícies das lamelas, usando uma linha dupla de cola para cada uma das cinco lamelas que compõem cada viga. Com uma área de superfície de 0,0575m² e uma gramatura de 200g/m², foram necessários 11,5g de adesivo e 2,3g de catalisador por linha de cola. A Figura 6 mostra a aplicação do adesivo com pincel na produção dos corpos de prova.

Figura 6
Aplicação de adesivo com utilização de pincel

Após a aplicação do adesivo, a viga foi prensada utilizando torquímetro e oito sargentos, conforme ilustrado na Figura 7. Para alcançar uma pressão de 1,2 MPa em madeiras de conífera, aplicou-se um torque de 6 N•m. Este método de colagem garantiu que a pressão aplicada não excedesse o limite de compressão normal às fibras da madeira, evitando assim o esmagamento do material. Conforme a norma NBR 7190-1 (ABNT, 2022a), a pressão mínima recomendada é de 0,7 MPa para madeiras com densidade até 0,5 g/cm³ e de 1,2 MPa para aquelas com densidade superior a 0,5 g/cm³.

Figura 7
Prensagem e cura das vigas

Ensaios experimentais realizados

Os elementos de MLC foram fabricados com dimensões de 5 cm × 5 cm × 115 cm e uma distância entre apoios de 105 cm, mantendo a relação L/h>20 para minimizar o efeito do cisalhamento na deformação (flecha) ao meio do vão. Essas dimensões foram escolhidas também em função das capacidades da máquina de ensaios. Os ensaios de flexão, conforme a norma, envolveram o carregamento por meio de uma carga concentrada no centro do vão, aplicada em dois ciclos de carga e descarga. Durante os testes utilizou-se um transdutor de deslocamento para medir a flecha em cada etapa do carregamento. O transdutor foi removido ao se alcançar 70% da carga máxima prevista para evitar danos ao equipamento. Os detalhes desses ensaios de flexão na EMIC (DL-30000) podem ser vistos na Figura 8.

Figura 8
Ensaio de flexão simples em viga de MLC

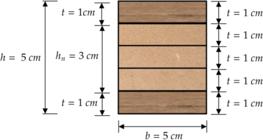
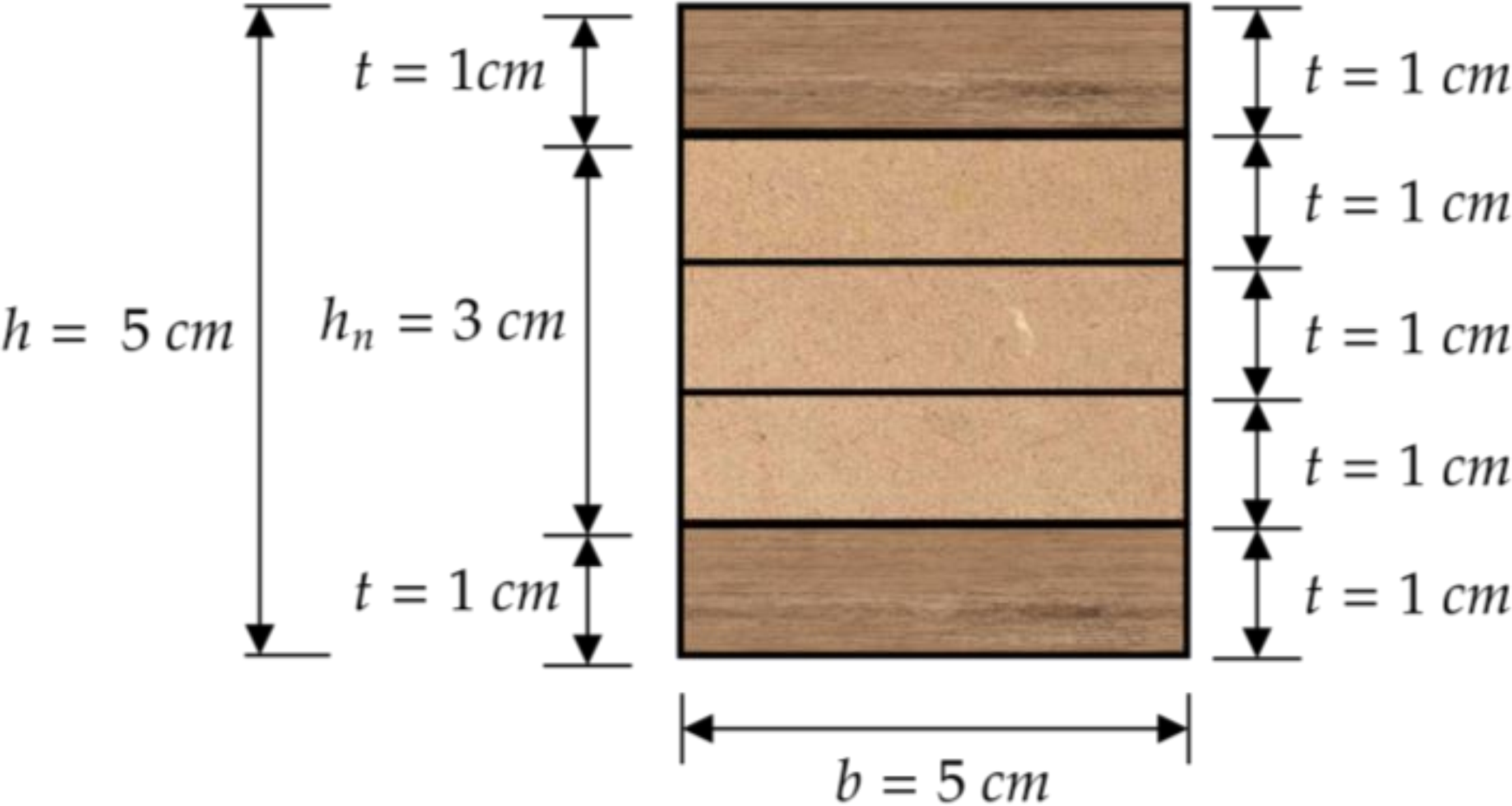
Para o uso das Equações 10, 12, 14, 16 e 17 na estimativa da rigidez a flexão das vigas de MLC avaliadas na presente pesquisa, sendo de 1 cm a espessura de cada uma das cinco lamelas, a espessura t das faces da seção é de 1 cm, sendo de 3 cm a altura do núcleo (h_n). Conforme representado pela Figura 9.

Figura 9
Representação da consideração das espessuras das lamelas para avaliação da estimativa de rigidez

Análise numérica

Na análise numérica de elementos de MLC foi performada utilizando o software ANSYS e empregado o elemento finito SOLID45, apropriado para simulações tridimensionais de sólidos que podem suportar grandes deformações. A seleção desse elemento é crucial, pois permite uma modelagem precisa das características mecânicas dos materiais, como as madeiras de pinus utilizadas no estudo. Esses materiais possuem propriedades elásticas e plásticas específicas, que foram incorporadas ao modelo para representar fielmente seu comportamento sob diferentes condições de carga.

A configuração da malha de elementos finitos é uma etapa fundamental no processo de simulação, pois uma malha bem definida e adequada é essencial para capturar com precisão as deformações e as distribuições de tensão nos elementos analisados. A adequação da malha impacta diretamente na qualidade dos resultados obtidos, influenciando a capacidade do modelo de simular o comportamento estrutural real dos elementos de MLC sob cargas aplicadas.

Na modelagem numérica de elementos em MLC, o comportamento ortotrópico da madeira é uma consideração crítica, visto que a madeira apresenta propriedades mecânicas distintas nas direções longitudinal, radial e tangencial. Esta característica ortotrópica é modelada através de relações constitutivas específicas, que definem como o material responde a tensões em diferentes direções. Para capturar adequadamente essas respostas, o modelo constitutivo adotado incluiu módulos de elasticidade e coeficientes de Poisson variáveis, que são essenciais para refletir o comportamento real da madeira sob cargas.

O modelo constitutivo utilizado incorpora as propriedades elásticas da madeira, permitindo que a simulação aborde deformações elásticas considerando a anisotropia desse material, dependendo das condições de carga aplicadas. Esse modelo é fundamental para o estudo do comportamento dos elementos de MLC, pois as propriedades ortotrópicas da madeira influenciam diretamente a integridade estrutural e o desempenho dos elementos sob diferentes tipos de carregamentos.

Neste contexto, a aplicação de carregamentos nos modelos numéricos foi realizada de maneira a replicar as condições experimentais. Esta abordagem envolve a definição cuidadosa das condições de contorno e das vinculações, estabelecendo restrições em graus específicos de liberdade conforme necessário para representar de maneira precisa os apoios e as condições de suporte dos elementos estruturais. Os modelos analisados foram configurados para refletir as condições dos ensaios experimentais, conforme ilustrado na Figura 10 e Figura 11. Os nós dos elementos empregados nos modelos possuíam três graus de liberdade, correspondendo às translações nas direções x, y e z (coordenadas locais).

Figura 10
Vinculações de apoio em todos os graus de liberdade: translações em x, y e z

Figura 11
Vinculações de apoio em apenas dois graus de liberdade: translações em x e y, sendo o z liberado para se ter uma estrutura isostática

A precisão na aplicação de carregamentos e na configuração das condições de contorno é crucial para garantir que o modelo numérico reflita de maneira fidedigna as condições reais enfrentadas pelos elementos de MLC. Os carregamentos foram replicados conforme os valores de cargas máximas aplicadas nos ensaios experimentais. Para isso, o valor da carga de ruptura foi distribuído entre os nós presentes na região central das vigas (elementos), que foi discretizada em um total de 12 nós, como mostrado na Figura 12.

Figura 12
Aplicação de carga nos 12 nós centrais do elemento.

Por fim, a validação dos modelos numéricos foi realizada através da comparação dos resultados obtidos com dados experimentais. Esta etapa é fundamental para verificar a acurácia dos modelos em prever o comportamento dos materiais e das estruturas simuladas. A análise dos resultados permite ajustar o modelo, se necessário, e confirmar sua eficácia como ferramenta de previsão das respostas estruturais de elementos de MLC.

Para a execução da análise numérica, foi performada uma análise linear, onde se presume que a rigidez do conjunto (elemento ou viga) se mantém constante. Conforme o carregamento é aplicado, a relação entre tensão e deformação (ou força e flecha) até a ruptura do sistema é linear, representada por uma única inclinação, K = Força/Flecha. Em outras palavras, à medida que a força aplicada aumenta, as deformações (ou flechas) crescem proporcionalmente. Essa abordagem linear foi adotada para calcular os valores de rigidez (EI) das vigas, determinados a partir de uma força P que induziu uma flecha de L/200. É importante notar que, para pequenas deflexões, a análise linear geralmente é adequada. A validade da teoria linear se restringe a este intervalo de baixas cargas. Na prática, em análise linear, especialmente em problemas resolvidos com a malha de elementos finitos, o problema é considerado resolvido uma vez que os cálculos estão completos, o que difere da análise não linear, onde fatores adicionais podem necessitar de consideração.

Quanto aos dados utilizados, a força P e os valores de deslocamento obtidos por simulação numérica foram inseridos na Equação 21, previamente mencionada, para calcular o valor de EI. Esta equação foi crucial para quantificar a rigidez das vigas em estudo.

Critérios estatísticos, modelo de estimativa e análise dos dados

O teste de Tukey para contraste de médias foi aplicado com um nível de significância de 5% para comparar a equivalência entre as médias dos valores de rigidez à flexão obtidos experimentalmente e os valores estimados de EI através de modelos e simulação numérica. Neste teste, o grupo A representa o conjunto com o maior valor médio, seguido pelo grupo B com o segundo maior valor médio, e assim por diante. Grupos que compartilham a mesma letra são considerados estatisticamente equivalentes em termos de suas médias.

Tendo por base o modelo para a estimativa da EI conforme a norma brasileira de estruturas de madeira (Equação 10) como referência, a Equação 23 consiste em alternativa que visa melhorar a precisão da equação originalmente proposta, sendo α₀ e α1 os parâmetros a serem ajustados pelo método dos mínimos quadrados. Tratando-se de um modelo de mínimos quadrados, a qualidade do ajuste é determinada por meio do coeficiente de determinação (R²).

$E\cdot I={\alpha }_0 \cdot \left\{\chi \cdot \left[\frac{E_f\cdot b\cdot h^3}{96}+(7+\chi )\right]\right\}+{\alpha }_1;\chi =\frac{E_n}{E_f}$ (Eq. 23)

O erro percentual absoluto médio (MAPE - Equação 24) foi utilizado para o cálculo dos erros cometidos na estimativa da rigidez a flexão das vigas de MLC provenientes do uso das Equações 4 (norma), 12, 14, 16 e 17 assim como do uso do método dos elementos finitos em relação aos valores da EI obtidos experimentalmente (Equação 21).

$MAPE\left(\mathrm{\%}\right)=100\cdot \frac{1}{N}\cdot \underset{i=1}{\overset{N}{\Sigma }} ||\frac{E{I}_{es{t}_i}-E{I}_{ex{p}_i}}{E{I}_{ex{p}_i}}||$ (Eq. 24)

Da Equação 24, N é o número considerado de amostras (14 vigas de MLC), EI_esti é o valor estimado da rigidez a flexão (modelos analíticos e simulação numérica) e EI_esti é o valor da rigidez a flexão determinado experimentalmente de cada viga de MLC avaliada.

Resultados e discussões

Esta seção detalha a análise dos resultados experimentais obtidos através dos ensaios de flexão de vigas de MLC de Pinus e compara estes resultados com as estimativas provenientes de modelos analíticos e simulações numéricas. Os objetivos principais desta análise foram verificar a conformidade dos dados experimentais com as previsões teóricas e avaliar a aplicabilidade das normas técnicas atuais no dimensionamento de tais estruturas.

Análise dos resultados experimentais

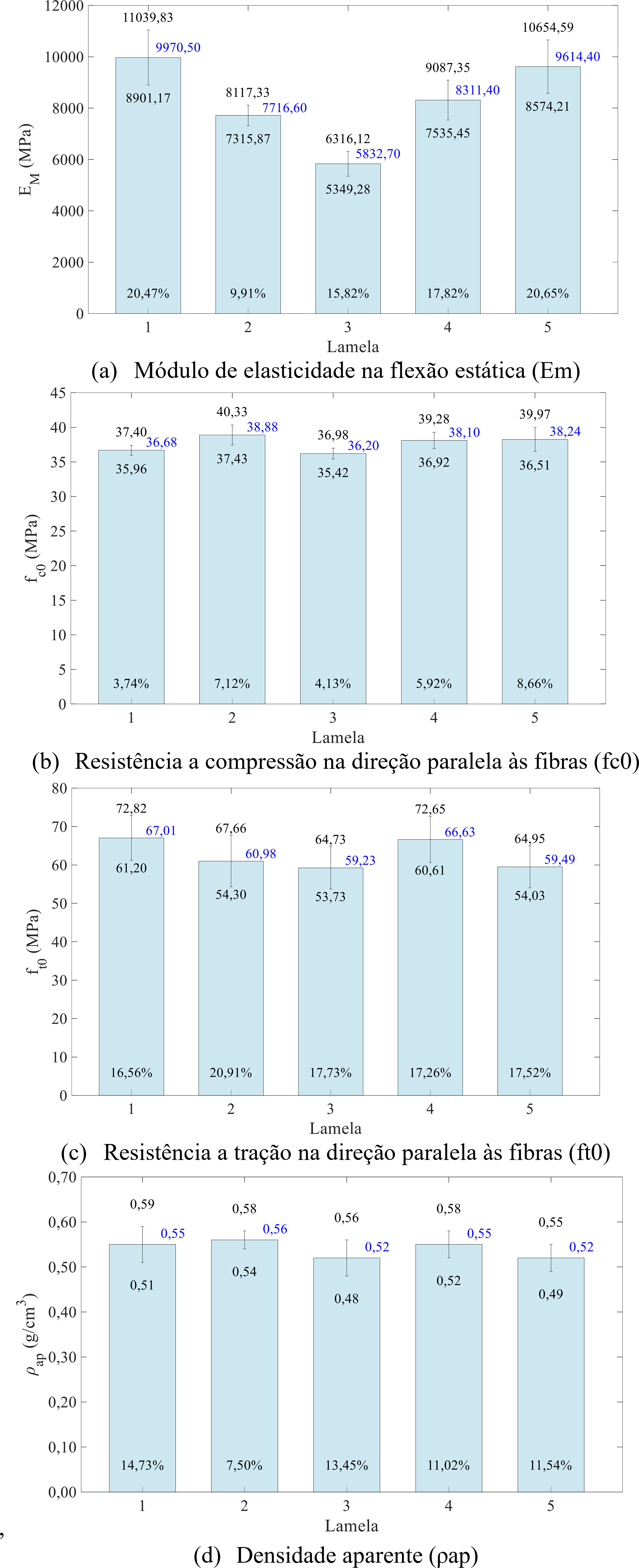
A Figura 13 apresenta os valores médios, os intervalos de confiança da média (95% de confiabilidade) e os coeficientes de variação (%) do módulo de elasticidade na flexão estática (E_m), da resistência a compressão na direção paralela às fibras (f_c0), da resistência a tração na direção paralela às fibras (f_t0) e da densidade aparente (ρ_ap) referente as lamelas utilizadas na composição das 14 vigas de MLC.

Figura 13
Síntese dos resultados das propriedades avaliadas

O valor característico da resistência à compressão, baseado em 70 amostras, é de 33,53 MPa, classificando a madeira de Pinus na categoria C30 do grupo das coníferas, de acordo com a norma NBR 7190-1 (ABNT, 2022a). A partir dessas amostras, foram determinados os valores médios e os coeficientes de variação para o módulo de elasticidade (E_m), resistência à compressão paralela às fibras (fc0), resistência à tração paralela às fibras (f_t0) e densidade aparente (ρ_ap), que foram respectivamente 8289 MPa (25,40%), 37,62 MPa (6.66%), 62,7 MPa (18,33%) e 0,54 g/cm³ (11,93%).

A análise dos dados apresentados na Figura 13 e comparações com estudos anteriores revelam consistência nos resultados. Aira, Arriaga e Íñiguez-González (2014) encontraram um módulo de elasticidade médio de 10283 MPa para a espécie Pinus sylvestris L. Em um estudo semelhante, Mederski et al. (2015) registraram uma resistência à compressão paralela às fibras de 39.26 MPa para a mesma espécie. Kim e Mishiro (1998), estudando a resistência mecânica ao longo do comprimento da árvore de Pinus koraiensis na Região Sul da Coreia, observaram valores médios de resistência de 38,74 MPa, 36,68 MPa e 40,21 MPa.

Comparação com modelos analíticos e numérico

Na Tabela 1 são apresentados os valores da rigidez a flexão (EI) obtidos experimentalmente (EI_exp), com o uso das Equações 10 (EI_{Eq. 10}), 12 (EI_{Eq. 12}), 14 (EI_{Eq. 14}), 16 (EI_{Eq. 16}) e 17 (EI_{Eq. 17}) e de forma numérica (EI_Num).

Tabela 1
Resultados obtidos da rigidez a flexão (EI – N·m2) obtidos experimentalmente, com o uso dos modelos analíticos e de forma numérica para as vigas de MLC

Viga	EIexp	EIEq. 10	EIEq. 12	EIEq. 14	EIEq. 16	EIEq. 17	EINum
X	5045,67	5007,98	4965,98	4973,29	4882,19	4882,19	4606,54
CV (%)	18,23	18,11	17,44	17,59	16,99	16,99	16,46
MAPE (%)	---	8,92	8,73	8,82	8,53	8,53	10,22
Tukey (5%)	A	A	A	A	A	A	A

No estudo da rigidez à flexão das vigas de MLC, constatou-se que as estimativas de EI derivadas tanto dos modelos analíticos quanto da simulação numérica foram consideradas equivalentes aos valores obtidos experimentalmente. Importante destacar que a simulação numérica não proporcionou uma maior precisão em relação aos modelos analíticos tradicionais, demonstrando que estes últimos possuem uma robustez comparável na estimativa de EI. Tal constatação é fundamental para justificar a adoção das expressões previstas na norma, visto que a equivalência entre as diferentes metodologias de cálculo reforça a confiabilidade e a aplicabilidade da normativa técnica vigente para o dimensionamento estrutural em projetos de engenharia.

Para avaliar a precisão e a variabilidade dos diferentes métodos, foram utilizados três indicadores estatísticos principais: o Coeficiente de Variação (CV), o Erro Percentual Absoluto Médio (MAPE) e o teste de Tukey. O Coeficiente de Variação, que mede a dispersão dos dados em relação à média, mostrou-se abaixo de 20% para todos os métodos, indicando uma variabilidade moderada e aceitável. O MAPE, que quantifica o erro médio em termos percentuais, variou de 8,53% a 10,22%, revelando que as estimativas dos modelos estão em boa concordância com os valores experimentais. A aplicação do teste de Tukey, uma análise pós-hoc, categorizou todas as metodologias no grupo A, demonstrando que não há diferenças estatisticamente significativas entre os valores médios de rigidez à flexão estimados pelos diferentes modelos e aqueles obtidos experimentalmente.

Esses resultados são relevantes para a prática de engenharia, pois confirmam a eficácia dos modelos analíticos e da simulação numérica no design e na avaliação de vigas de MLC. A consistência entre os métodos fornece uma base sólida para os engenheiros ao escolherem a metodologia de cálculo, fundamentada não apenas na precisão, mas também na facilidade de implementação e no custo, assegurando a aplicação eficiente das normas técnicas em projetos estruturais.

Conclusões

Este estudo proporcionou uma compreensão aprofundada sobre a rigidez à flexão de vigas de MLC de Pinus, utilizando tanto métodos analíticos quanto simulações numéricas. Os resultados obtidos demonstram que os modelos analíticos tradicionais são capazes de prever a rigidez à flexão (EI) com uma precisão comparável às estimativas obtidas por simulação numérica, o que reforça a validade das expressões normativas atuais para o dimensionamento de vigas em MLC.

Foi observado que as diferenças entre os valores de EI obtidos experimentalmente e aqueles estimados pelos modelos não excederam 10% em termos de erro percentual absoluto médio (MAPE), indicando uma boa concordância geral entre as abordagens teóricas e os dados experimentais. Este estudo também destaca a importância de considerar a variabilidade nas propriedades mecânicas das lamelas, que influenciam diretamente a performance estrutural das vigas de MLC.

Além disso, a análise dos resultados contribui para a validação das normativas técnicas utilizadas no Brasil (ABNT, 2022a), reforçando a aplicabilidade das metodologias de cálculo da rigidez em projetos de engenharia civil que utilizam madeira de reflorestamento. O uso de madeira de Pinus, proveniente de manejo sustentável, não só oferece vantagens ambientais, como também apresenta características técnicas competitivas para aplicações estruturais.

Portanto, este trabalho não apenas confirma a eficácia dos modelos estudados para a previsão de EI em vigas de MLC, mas também reitera o potencial do uso de recursos renováveis e técnicas de engenharia avançada para promover uma construção mais sustentável e eficiente. Estudos futuros poderão expandir estas análises para outras espécies de madeira e configurações de vigas, visando a otimização contínua de materiais e métodos de construção em madeira engenheirada.

Referências

• ADAMOPOULOS, S.; WIMMER, R.; MILIOS, E. Tracheid length: growth relationships of young Pinus brutia grown on reforestation sites. IAWA Journal, v. 33, n. 1, p. 39–49, 2012.
• ADILI, B.; EL AOUNI, M. H.; BALANDIER, P. Unravelling the influence of light, litter and understorey vegetation on Pinus pinea natural regeneration. Forestry, v. 86, n. 3, p. 297–304, 2013.
• AIRA, J. R.; ARRIAGA, F.; ÍÑIGUEZ-GONZÁLEZ, G. Determination of the elastic constants of Scots pine (Pinus sylvestris L.) wood by means of compression tests. Biosystems Engineering, v. 126, p. 12–22, 2014.
• ALTINOK, M.; BURDURLU, E.; ÖZKAYA, K. Deformation analysis of curved laminated structural wood elements. Construction and Building Materials, v. 22, n. 8, p. 1643–1647, 2008.
• AMERICAN SOCIETY FOR TESTING AND MATERIALS. D7250/D7250M-20: standard practice for determining sandwich beam flexural and shear stiffness. west Conshohocken, 2020.
• ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7190-1: projeto de estruturas de madeira. parte 1: critérios de dimensionamento. Rio de Janeiro, 2022a.
• ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7190-2: projeto de estruturas de madeira. parte 2: métodos de ensaio para classificação visual e mecânica de peças estruturais de madeira. Rio de Janeiro, 2022b.
• ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7190-6: projeto de estruturas de madeira: parte 6: métodos de ensaio para caracterização de madeira lamelada colada estrutural. Rio de Janeiro, 2022c.
• BALASBANEH, A. T.; SHER, W. Comparative sustainability evaluation of two engineered wood-based construction materials: Life cycle analysis of CLT versus GLT. Building and Environment, v. 204, p. 108112, 2021.
• CHEN, G. et al. A strong, flame-retardant, and thermally insulating wood laminate. Chemical Engineering Journal, v. 383, p. 123109, 2020.
• CHRISTOFORO, A. L.; LIBARDI, W. Mecânica dos sólidos e introdução aos métodos numéricos para engenharia civil São Carlos: Edufscar, 2019.
• CUNHA A.B. Produção de vigas estruturais de madeira avaliadas por meio de ensaios estáticos e dinâmicos Curitiba, 2007. 146 f. Tese (Doutorado em Engenharia Florestal) - Universidade Federal do Paraná, Curitiba, 2007.
• ESPELTA, J. M.; RETANA, J.; HABROUK, A. An economic and ecological multi-criteria evaluation of reforestation methods to recover burned Pinus nigra forests in NE Spain. Forest Ecology and Management, v. 180, n. 1/3, p. 185–198, 2003.
• FERDOUS, W.; MANALO, A.; ARAVINTHAN, T.; FAM, A. Flexural and shear behaviour of layered sandwich beams. Construction and Building Materials, v. 173, p. 429–442, 2018.
• FIORELLI, J.; DIAS, A. A. Glulam beams reinforced with FRP externally-bonded: theoretical and experimental evaluation. Materials and Structures, v. 44, n. 8, p. 1431–1440, 2011.
• FLORES, E. I. S. et al Multi-scale model updating for the mechanical properties of cross-laminated timber. Computers & Structures, v. 177, p. 83–90, 2016.
• FRIQUIN, K. A Review of Models for the Charring Rate of Solid Wood, Nail- and Glue- Laminated Structural Members. Journal of Structural Fire Engineering, v. 1, n. 1, p. 61–72, 2010.
• GAO, S. et al. Mechanical Properties of Glued-Laminated Timber with Different Assembly Patterns. Advances in Civil Engineering, v. 2019, p. 1–13, 2019.
• KIM, B.-R.; MISHIRO, A. Studies on variability of wood properties in stem of pinus koraiensis (II): differences in tracheid length, microfibril angle, and compression strength in south and north sides of stem. Journal of the Korean Wood Science and Technology, v. 26, n. 2, p. 45–50, 1998.
• LEVY NETO, F.; PARDINI, L. C. Compósitos estruturais: ciência e tecnologia. 2. ed. São Paulo: Blucher, 2016.
• LI, S.; ZHANG, Y. Experiment on the impact response of aluminum alloy wood core sandwich composites. Advances in Mechanical Engineering, v. 15, n. 11, p. 1-25, 2023.
• MALLO, M. F. L.; ESPINOZA, O. Awareness, perceptions and willingness to adopt Cross-Laminated Timber by the architecture community in the United States. Journal of Cleaner Production, v. 94, p. 198–210, 2015.
• MEDERSKI, P. S. et al. Density and mechanical properties of Scots Pine (Pinus sylvestris L.) wood from a seedling seed orchard. Drewno Wood, v. 58, n. 195, p. 117–124, 2015.
• MOLINA, J. C. (org.). A madeira na engenharia: teoria, experimentação e simulação: uma visão geral sobre a análise deste nobre material. London: Novas Edições Acadêmicas, 2017.
• NADIR, Y. et al. Flexural stiffness and strength enhancement of horizontally glued laminated wood beams with GFRP and CFRP composite sheets. Construction and Building Materials, v. 112, p. 547–555, 2016.
• NAMARI, S. et al. Mechanical properties of compressed wood. Construction and Building Materials, v. 301, p. 124269, 2021.
• PEIXOTO, L. S. et al. Bending behavior of steel bars reinforced Glulam beams considering the homogenized cross section. Wood Material Science & Engineering, v. 17, n. 6, p. 533–539, 2022.
• SORIANO, J.; PELLIS, B. P.; MASCIA, N. T. Mechanical performance of glued-laminated timber beams symmetrically reinforced with steel bars. Composite Structures, v. 150, p. 200–207, 2016.
• TELES, R. F. et al. Effect of nondestructive testing of laminations on the bending properties of glulam beams made from louro-vermelho (Sextonia rubra). CERNE, v. 16, n. 1, p. 77–85, 2010.
• YADAV, R.; KUMAR, J. Engineered wood products as a sustainable construction material: a review. In: GONG, M. (org.). Engineered wood products for construction London: IntechOpen, 2022.

Editado por

• Editor:
  Marcelo Henrique Farias de Medeiros

Datas de Publicação

• Publicação nesta coleção
  16 Maio 2025
• Data do Fascículo
  Jan-Dec 2025

Histórico

• Recebido
  13 Maio 2024
• Aceito
  24 Mar 2025