Abstract
A model is proposed for the average effective diffusivity for an arbitrary pore size distribution. It is shown that the average diffusivity must also depend on the distribution of the catalyst sites. The reaction diffusivity is compared with the average diffusivities defined by Wakao and Smith (1962) and Johnson and Stewart (1965). For the methanol dehydration and n-butene isomerization, the reaction diffusivity gives a better estimation of the effectiveness factor than the other models
Reaction diffusivity; porous catalyst; dehydration; isomerization
THE SENSITIVITY OF THE CATALYST EFFECTIVENESS FACTOR TO PORE SIZE DISTRIBUTION
Z. Bensetiti 1 , D. Schweich 1 and C.A.M. Abreu 2
1 Laboratoire des Sciences de Génie Chimique, CNRS-ENSIC/INPL
Rue Grandville, 54001 Nancy, France
2 Departamento de Engenharia Química/Universidade Federal de Pernambuco - 50.740-521 Recife-PE, Brazil
(Received: December 13, 1996; Accepted: August 5, 1997)
Abstract: A model is proposed for the average effective diffusivity for an arbitrary pore size distribution. It is shown that the average diffusivity must also depend on the distribution of the catalyst sites. The reaction diffusivity is compared with the average diffusivities defined by Wakao and Smith (1962) and Johnson and Stewart (1965). For the methanol dehydration and n-butene isomerization, the reaction diffusivity gives a better estimation of the effectiveness factor than the other models.
Keywords: Reaction diffusivity, porous catalyst, dehydration, isomerization.
INTRODUCTION
The concept of effective diffusivity in porous catalyst is widely used to assess the importance of diffusion limitations to chemical reactions. When there is a pore size distribution, different methods yield mean effective diffusivities which may differ by more than an order of magnitude. The steady-state and transient Wicke-Kallenbach experimental methods (Baiker et al., 1982; Kawazoe and Takenchi, 1974; McGravy and Siddiqui; 1980) are currently used to estimate this quantity. Different estimations by chromatographic and thermosorption transient methods (Otani and Smith, 1968; Park and Kim, 1976; Steised and Butt, 1967; Cui et. al., 1989) have shown discrepancies between values of the effective diffusivities for a given solute/porous system. The numerical values for the effective diffusivity can differ according to the model used and the pore size distribution. One may also recognize that the distribution of the catalytic sites would affect the effectiveness factor. It is expected that the diffusion resistance is more severe in narrow pores than in wide pores, and that the density of the catalytic sites per area is greater in the wide pores then in the narrow ones. Wakao and Smith (1962) were probably the first authors to recognize that effective diffusivity depends on the reaction properties when they proposed a theoretical description of the diffusion process in a catalyst having a bimodal pore size distribution. Their results are restricted to the first order reaction and require knowledge of the effectiveness factor in the narrow pores. Johnson and Stewart (1965) pointed out that the geometrical structure of the pore network must be accounted for when estimating effective diffusivity. They have assumed that the pores are not interconnected and that both the local porosity and the tortuosity factor are independent of the pore radius. In this work a new effective diffusivity is derived wich accounts for any pore size distribution and catalytic site distribution. The so-called reaction diffusivity is estimated by the reaction method deduced from the dependence of the effectiveness factor upon the Thiele modulus. The reaction diffusitivy model is compared to the Wakao-Smith (1962) and Johnson-Stewart (1965) models to discover whether one definition is more reliable than another. The diffusion models are compared in a attempt to interpret the experimental conversion data for the methanol dehydration and n-butene isomerization.
THE REACTION DIFFUSIVITY
The effective diffusivity of a porous catalyst can be looked at with respect to the underlying physical processes such as diffusion in the pore fluid. In this case when Knudsen and molecular diffusion compete, the estimation of the diffusivity is given by:
 (1)
(1)
where b is the porosity of the particle, t the tortuosity factor, R the mean pore radius and Dm and Dk the molecular and the Knudsen diffusivities, respectively.
In real solid catalysts, pore radii are distributed and two models are frequently used to account for
pore size distribution. In Johnson and Stewarts approach (Johnson and Stewart, 1965), the solid particle is assumed to be composed of subparticles placed in parallel. Each subparticle has pores of the same radius R, whereas different subparticles have pores of different radii. Assuming that the pores are not interconnected, and that the local porosity b and the tortuosity factor t are independent of the pore radius, the effective diffusivity (DJS) is given by the Johnson-Stewart model :
 (2)
(2)
where D(R) is the homogeneous fluid diffusion coefficient for pores with radius R and f(R) is the pore size distribution. Wakao and Smith (1962) proposed another model to account for bimodal pore size distribution with macro and micropores connected at random. The Wakao-Smith diffusivity (DWS) is given by :
 (3)
(3)
with DM and Dm being the diffusivities in the homogeneous pore fluid of pore of the widest and narrowest pores and b M and b m being the void fractions attributed to wide and narrow pores, respectively.
The evaluation of chemical reactions in catalytic processes can be quantified by the effectiveness factor estimated from the general equation established by Froment and Bischoff (1965) :
 (4)
(4)
where D(R) is the local effective diffusivity of the reactant, r(R,C) the kinetic rate and Cs and Cc the concentrations at the boundary and at the center of the catalyst slab with a thickness of 2L. The effectiveness factor depends on both the pore size distribution through D(R) and the catalytic site distribution.
Bearing in mind the effectiveness factor definition and also taking into account the pore size distribution of the catalyst, it becomes pertinent to define the apparent reaction rate averaged over the pore radii distribution, f(R), expressed by :
 (5)
(5)
Assuming r(R,C) as the intrinsic kinetic rate of a single irreversible nth order reaction, the average kinetic rate is given by:
 (6)
(6)
where r(R,C)=k(R)g(C). Various assumptions can be made concerning k(R). The simplest consists of assuming that the number of catalytic sites per unit area of pore wall is constant. For cylindrical pores, the surface area of pores with radius R per unit volume of catalyst is given by a(R)=2b /R. Then,
 (7)
(7)
where kA is the kinetic rate constant per unit area of pore wall. Under strong diffusional limitations, h S=1/f s, where:
 (8)
(8)
This shows that the effective diffusivity, DRE , depends on pore size distribution and on catalytic site distribution. Under these conditions, when the reagent concentration in the center of the catalyst slab reaches the equilibrium value, Ceq, whatever the pore radius, the effectiveness factor h can be estimated by combining equations (4), (5) and (6) to obtain :
 (9)
(9)
Based on the Thiele modulus defined by equation (8), the effective diffusivity, DRE, under reaction conditions is obtained :
 (10)
(10)
where l is given by:
 (11)
(11)
For an irreversible nth order reaction in catalyst pellets having cylindrical pores, the reaction diffusivity can be estimated by combining equations (7), (8) and (10), to obtain :
 (12)
(12)
Equations (2), (3) and (12) can be used to calculate the effective diffusivities on the basis of the diffusion coefficient in the homogeneous pore fluid given by equation (1).
EXPERIMENTAL
The system taken into account under reaction conditions has been studied in a classical fixed-bed installation. The laboratory-scale packed bed reactor system consists of three parts: the feed section, the packed bed reactor and the chromatograph. The ragent is pumped to the feed section under constant flow with a HPLC pump at 298 K where it is mixed with nitrigen and heated at 423 K. The flow rate of the heated mixture into the reactor ( 0.04 m high and with a diameter of 0.015 m ) varied within a range from 0.21x10-3 m3 s-1 to 11.74x10-3m3 s-1 .The flow inside the bed packed with catalyst is assumed to be isobaric and isothermal. The catalyst employed was a g -alumina from Rhone-Poulenc, reference GCO-70. Table 1 shows the properties of g -Al2O3/GCO-70. Figure 1 shows the catalyst pore size distribution obtained by a mercury porosimeter Milestone 200. Specific surface was determined by the BET method using a Micromeritics 2000 Sorptemeter. Tortuosity was estimated by diffusion experiments using tracer technics (Cui. et al.,1989) with the same catalyst and gas tracer/carrier couples, Ar-He, N2-He and CH4-He. The experiments were carried out at atmospheric pressure between 433 K and 558 K, for dehydration of the methanol, and between 473 K and 743 K for the isomerization of n-butene. To obtain the experimental results in the diffusion and chemical regimes, mixtures of 5 % v/v of methanol and nitrogen or n-butene and nitrogen were fed at space time between 0.30 s and 4.40 s for the former reaction and 20 s and 90 s for the latter. Runs were carried out using catalyst slabs of diameter of 0.20 cm. Samples at the reactor outlet were analyzed by gas chromatography to identify the presence of methanol and dimethyl ether in the dehydration of methanol and n-butene, 2-cis-butene and 2-trans-butene in the isomerization of n-butene. A stainless steel column Porapak-PS with a length of 200 cm and a internal diameter of 1/8" was used, with a Delsi 200 chromatograph with a FID detector on line.
RESULTS AND DISCUSSION
The experiments were performed with a fresh catalyst and the space time of the gas (q ) was varied within in a range from 0.31s to 4.38 s for the methanol reaction and from 0.36 s to 1.61 s for n-butene. Tables 2 and 3 show the experimental results under reaction conditions for the dehydration of methanol and isomerization of n-butene, respectively.
Figure 1: The catalyst size distribution (g -Al2O3/GCO-70).
Table 1: Characteristics of the catalyst g -Al 2 O 3 /GCO-70
The average diffusivities of methanol and n-butene in nitrogen inside the g -alumina GCO-70 catalyst were estimated using the accumulative pore size distribution which is given in Figure 1 and the properties listed in Table 1. Wakao and Smith diffusivities were calculated with Rm =10 nm and RM=100 nm. Table 4 summarizes the effective diffusivities estimated in the range from 543K to 573K for the methanol and from 673K and 743K for the n-butene. The order of the values of the diffusivities obtained was as follows : DJS>DWS>DRE.
The Johnson and Stewart diffusivity describes steady-state diffusion without reaction. Consequently, the widest pores make a large contribution to the average diffusivity. This contribution is smaller in Wakao and Smith diffusivity because the widest pores are assumed to be partially obstructed by solid elements containing the micropores. Finally, the reaction diffusivity favors the pores with the highest catalytic activity, i.e., the micropores where the diffusivity is the smallest. Discrepancies between values of the effective diffusivities obtained from experimental results and those antecipated from theoretical models, were observed. It is possible to accept this difference due to estimations based on pseudo-homogeneous models. In the experimental methods the effective diffusivities are determined based on global values, such as the mass flux (Wicke and Kallenbachs methods), diffusion time (transient methods) and reaction methods which are related in specific forms . Burghardt et al. (1988) compared the measured stedy-state and transient diffusivities values. It was noted that in the first case the coefficients are higher then those obtained at transient regime. Mo and Wei (1986) noted that the estimated diffusivities in presence of a chemical reaction are lower than those obtained without chemical reaction calculated by Wakao and Smith method. Since the various average diffusivities are different, it is of prime importance to known wether one definition is more reliable than another. Because of the many simplifying assumptions made in each diffusion model, it is impossible to unambiguously prove that one model is better than another for estimating the intrinsic kinetic rate in order to estimate the effectiveness factor. The problem is even more challenging because we need to know the intrinsic kinetic rate for testing the reliability of a diffusion model. However, to know the intrinsic kinetic rate, we need to estimate the potential diffusion limitation in other words, we need to know the effective diffusivity. To overcome this paradox, we will compare the diffusion models and try to interpret the experimental conversion data with fitted intrinsic kinetic parameters, with all other parameters (diffusivity, physical properties of catalyst) having fixed values. To be efficient, this method must be applied to a set of experimental results in the diffusion and chemical regimes. We have studied two slightly exothermic and equimolar reactions where diffusion is the only process responsible for mass transfer inside the catalyst. The volumetric flow rate was sufficiently high to make external film resistance negligible. The dehydration of methanol (MeOH) in dimethyl ether (Me2O) and water (W) (scheme 1) and the isomerization of n-butene (nBut) in cis-2-butene (cBut) and trans-2-butene (tBut) (scheme 2) were catalyzed by g -Al2O3/GCO-70 and chosen as experimental examples.
Using the classical Weisz criterion (Weisz, l962), it was found that the chemical reaction controlled the rate in the lower temperature ranges, from 433K to 463K for the dehydration of methanol and from 473K to 513K for the isomerization of n-butene, whereas diffusion controlled the rate in the higher temperature ranges, from 543K to 573K for the former reaction and from 673 K to 743 K for the latter.
Assuming the dehydration of methanol to be second order (Knozinger and Kochloefl, 1973; Lapidus and Petersen, l965) and the isomerization of n-butene to be first order (Hightower and Hall, 1968; Forni and Zanderighi,1968), then the rate laws are given as follows :
 (13)
(13)
where CMeOH is the feed concentration of methanol, XMeOH the conversion fraction and KMeOH the equilibrium constant;
 (14)
(14)
Scheme 1: The dehydration of methanol.
Scheme 2: The isomerization of n-butene.
where CnButo is the feed concentration of n-butene, ` k12=` k1 +` k2 and XnBut the conversion fraction of n-butene. The equilibrium constant is given by KBut= KcBut (1+KtBut), where KcBut and KtBut are the equilibrium constants for both steps of isomerization of the n-butene/cis-2-butene and n-butene/trans-2-butene. The activation energies and the frequency factors have been fitted in the temperature ranges in the chemical regimes. In the low temperature range, the reactions are almost irreversible. By fitting the kinetic parameters of the forward reactions, we have obtained the values listed in Table 5. Assuming the rate laws for the dehydration of methanol and the isomerization of n-butene, the activation energy (E) and the frequency factor (k0) have been fitted in the full temperature range. The values in Table 5 are used to initialize an optimization procedure (Box, 1965) based on the mass balance equations utilized on the full temperature range for the both reactions by introducing the estimations of effectiveness factor.
The three diffusivity models are compared by fitting the intrinsic kinetic parameters k0 and E. This procedure introduces modifications in the values of the initialized parameters which reduce the differences between the calculated conversions by the models and those obtained by experiments. The effectiveness factors are calculated by equation (4), using the effective diffusivities listed in Table 4. For dehydration of methanol,
 (15)
(15)
Applying equation (15), and assuming that the dehydration is second order, yields :
 (16)
(16)
where the values of CMeOHc can be estimated by:
 (17)
(17)
The optimized final values of the parameters are obtained by defining a quadratic objective function (f0), as  where
where  and
and  are the experimental and calculated conversions for methanol and n-butene. The results obtained for the dehydration of methanol are given in Table 6.
are the experimental and calculated conversions for methanol and n-butene. The results obtained for the dehydration of methanol are given in Table 6.
For the methanol Figures 2, 3 and 4 show the agreement between experimental and calculated conversions . It can be seen that from the three effective diffusivity models used to reproduce the experimental data of methanol conversions the one which shows the best agreement is the reaction diffusivity model. The comparison of the Wakao-Smith and Johnson-Stewart models does not show measurable differences between them.
Figure 2: Experimental vs. calculated conversion fractions of methanol for the dehydration of methanol based on the Wakao-Smith diffusivity model.
Figure 3: Experimental vs. calculated conversion fractions for the dehydration of methanol based on the Johnson-Stewart diffusivity model.
Figure 4: Experimental vs. calculated conversion fractions for the dehydration of methanol based on the reaction diffusivity model.
In the case of n-butene where reaction of isomerization was assumed to be first order, the effectiveness factor was obtained by:
 (18)
(18)
Since the effectiveness factor of n-butene is independent of concentration, one should compare the values obtained on the basis of experimental conversions with those estimated by (19). Thus, the experimental effectiveness factor can be given as follows:
 (19)
(19)
In Table 7 the values of the effectiveness factors estimated by (19) are listed and these values were obtained by using equation (18) with the diffusivities estimated from the Wakao-Smith, Johnson-Stewart and reaction diffusivity methods for isomerization of n-butene. It was found that the effectiveness factors for isomerization of n-butene obtained by the reaction diffusivity model give a better representation of the experimental results.
In both the process of dehydration of methanol and isomerization of n-butene, the estimation of the reagent conversions showed better predictions when effectiveness factors were calculated on the basis of an effective diffusivity model adequate for heterogeneous catalysis developed for porous solid catalysts. Over estimated effective diffusivity values, based on the Wakao-Smith and Johnson-Stewart models, justify the expected differences of the conversions based on these models in relation to the experimental conversions of methanol and n-butene.
CONCLUSIONS
A new effective diffusivity called reaction diffusivity was obtained wich accounted for all pore and catalytic site distributions on the basis of two experimental examples. The results indicate that reaction diffusivity can be reliable for estimating the effectiveness factor. The reaction diffusivity is compared with the average diffusivities defined by Wakao and Smith and Johnson and Stewart. To interpret the experimental conversion data for methanol dehydration and n-butene isomerization, the reaction diffusivity was compared with the average diffusivities defined by Wakao and Smith and Johnson and Stewart. In both processes the estimation of the reagent conversions showed better predictions when effectiveness factors were calculated on the basis of the effective reaction diffusivity.
ACKNOWLEDGMENTS
The authors acknowledge the financial support received from CNRS/France and CAPES/Brazil.
NOMENCLATURE
k1o
k12o
Frequency factor of dehydration of the methanol
Frequency factor of isomerization of the n-butene
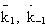
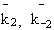
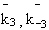
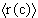
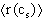
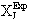
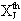
Greek
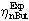
f
Thieles module
REFERENCES
Baiker, A.; New, M., and Richarz, W., Determination of Intraparticle Diffusion Coefficients in Catalyst Pellets. A Comparative Study of Measuring Methods, Chem. Eng. Sci. 37, 643 (1982).
Box, P., A New Method of Constrained Optimization and a Comparison with Other Methods, Computer Journal, 8, 42 (1965).
Burghardt, A. and Rogut, J., Diffusion Coefficients in Bidisperse Porous Structures, Chem. Eng. Sci., 43, 2463 (1988).
Cui, C.L.; Schweich, D. and Villermaux, J., Influence of the Pore Diameter on the Determination of Effective Diffusivity in Porous Catalysts., Chem. Eng. Process., 26, 121 (1989).
Froment, G.F. and Bischoff, K.B., Chemical Reactors Analysis and Design, Wiley and Sons, N.Y. (1979).
Forni, L. and Zanderighi, L., Kinetic Study of 1-Butene Isomerization on Alumina., J. of Catalysis 12, 298 (1968).
Hightower, J.W. and Hall, W.K., Butene Isomerization Over Oxide Catalysts, AIChe Symp. Series (1968).
Johnson, M.F.L. and Stewart, W.E., Pore Structure and Gaseous Diffusion in Solid Catalysts, J. of Catalysis 4, 248 (1965).
Kawazoe, K. and Takenchi, A., Mass Transfer in Adsorption on Bidisperse Porous Materials. Macro and Micropores Series Diffusion Models., J. Chem. Eng. Japan 7, 431 (1974).
Knozinger, H. and Kochloefl, K., Kinetics of Bimolecular Ether Formation from Alcohols Over Alumina, J. of Catalysis, 28, 69 (1973).
Lapidus, L. and Petersen, T. I., Analysis of Heterogeneous Catalytic Reactions by Nonlinear Estimation., AIChe Journal, 11, 891 (1965).
McGravy, C. and Siddiqui, M.A., Consistent Measurements of Diffusion Coefficients for Effectiveness Factors., Chem Eng. Sci., 35, 3 (1980).
Mo, W.T. and Wei, J., Effective Diffusivity in Partially Blocked Zeolite Catalyst., Chem. Eng. Sci., 41, 703 (1986).
Otani, S. and Smith, J. M., Effectiveness of Large Catalyst Pellet an Experimental Study., J. of Catalysis 5, 332 (1968).
Park, S.H. and Kim, Y.G., The Effect of Chemical Reaction on Effective Diffusivity within Biporous Catalysts., Chem. Eng. Sci. 31, 123 (1976).
Steised, N. and Butt, J.B., Prediction of Effective Diffusivities for Reacting Systems, Chem. Eng. Sci. 22, 469 (1967).
Wakao, N. and Smith, J.M., Diffusivities in Catalyst Pellets, Chem. Eng. Sci 17, 923 (1962).
Weisz, P. B. and Hicks, J. S., Chem. Eng. Sci. 17, 265 (1962).
Publication Dates
-
Publication in this collection
09 Oct 1998 -
Date of issue
Sept 1997
History
-
Accepted
05 Aug 1997 -
Received
13 Dec 1996







