A modified UNIQUAC equation for mixtures containing self-associating compounds

THERMODYNAMICS

A modified UNIQUAC equation for mixtures containing self-associating compounds

P. A. Pessôa FilhoI, ^*; R. S. MohamedII, ^†; G. Maurer^III

^IDepartamento de Engenharia Química, Escola Politécnica, Universidade de São Paulo, Phone: +(55) (11) 3091 1106, Fax: +(55) (11) 3091 2284, C. P. l 61548, CEP 05424-970, São Paulo - SP, Brazil. E-mail: [e-mail]

^IIDepartamento de Termofluidodinâmica, Faculdade de Engenharia Química, Universidade Estadual de Campinas, Cx. P. 6066, CEP 13083-970, Campinas - SP, Brazil

^IIILehrstuhl für Technische Thermodynamik, Universität Kaiserslautern, Postfach 3049, D-67653, Kaiserslautern, Germany

ABSTRACT

The UNIQUAC model for the excess Gibbs energy is modified using chemical theory to account for chain-like association occurring in self-associating compounds such as alcohols. The equation considers the alcohol to be a mixture of clusters in chemical equilibrium. The UNIQUAC equation is used to model the behavior of the mixture of clusters, with size and surface parameters related to the number of alcohol molecules involved in their formation. The values of association enthalpy and entropy were obtained through fitting vapor pressure data. The model is used to correlate phase behavior of alcohol-hydrocarbon mixtures at low pressures, presenting excellent results in bubble point calculations. A further extension was made to allow for cross-association, the formation of a hydrogen bond between the molecules of an alcohol and an active solute. This extension was used to model alcohol-aromatic mixtures with equally good results.

Keywords: Model; Excess Gibbs energy; Vapor-liquid equilibria; Alcohol; Hydrocarbon.

INTRODUCTION

The fact that mixtures containing self-associating compounds show strong deviations from ideal behavior has long been recognized. The first important attempt to account for it in thermodynamic modeling was made by Kretschmer and Wiebe (1954), who regarded an alcohol as a mixture of linear clusters in chemical equilibrium. The deviation from ideal behavior in a mixture of these clusters and an inert compound was obtained using only the combinatorial part of the Flory-Huggins model.

The main assumption of Kretschmer and Wiebe is that the Gibbs energy of the general reaction:

is independent of i when occurring between isolated molecules. Furthermore, the volume of an oligomer is considered to be proportional to the number of monomer segments. This assumption, along with the Flory-Huggins equation for the Gibbs energy of mixing, leads to the expression:

in which j is the volume fraction and K is the equilibrium constant. After some rearrangements, one can relate the ratio:

to K through the expression:

wherein V_A1 represents the volume of the monomer and c is the concentration in amount of substance per volume. The dependence of K_i+1 on i, due to the diferences in oligomer volumes accounted for when the standard state is changed to the pure liquid, results in not depending on i.

When aromatic hydrocarbons are present, a cross-association or solvation reaction (between a hydrocarbon molecule and a molecule of any cluster) was considered to occur by Kretschmer and Wiebe (1954). The chemical equilibrium was then calculated using some mathematical simplification involving the arbitrary definition of the solvation equilibrium constant as a ratio of concentrations similar to K^C.

Renon and Prausnitz (1967) obtained almost the same expressions as Kretschmer and Wiebe (1954) through a more rigorous derivation; they, however, did not address the problem of cross-association. Nagata and Kawamura (1977) presented a modified UNIQUAC equation, based on the same assumptions of Kretschmer and Wiebe. In their work, the ratio of volume fractions:

was used to calculate the chemical equilibrium among clusters and was considered to be independent of concentration and cluster size. The authors also presented another model based on the Kempter and Mecke (1940) equilibrium constant. Nagata (1985) extended that model in order to tackle mixtures containing any number of alcohols and mixtures of an alcohol and an active compound (i. e, a compound that can undergo solvation).

Nath and Bender (1981a) proposed to use the normal boiling point temperature and the enthalpy of vaporization to obtain the value of the equilibrium constants. They recognized that the determination of equilibrium constants through experimental phase equilibrium and excess enthalpy data, as done hitherto, was inconvenient due to the necessary introduction of mixture data in the calculation of a property of a pure substance. The authors subsequently extended the proposed model to mixtures of one alcohol and inert compounds (Nath and Bender, 1981b) and to mixtures of any number of alcohols and inert compounds (Nath and Bender, 1983). It is worth noting that the authors used equation (5) for the equilibrium constant.

Brandani (1983) and Brandani and Evangelista (1984) published important papers on this subject. The authors did not define an equilibrium constant, as done in most previous studies, but instead used the UNIQUAC equation to obtain this equilibrium constant. In other words, they began with Flory's (1942) reference state (pure substance whose molecules are oriented in a crystalline arrangement) and then, through a series of steps, obtained an expression for the equilibrium constant, whose parameters (enthalpy and entropy of association) were found by fitting vapor pressure data; the gas phase was modeled using a truncated virial equation of state. Brandani and Evangelista (1984) replaced the crystalline state by the pure liquid as the reference state, in order to maintain consistency with the UNIQUAC model.

Recently, the Statistical Associated-Fluid Theory (SAFT) has found extensive application in the development of models for mixtures containing associating compounds (either for excess Gibbs energy or for volumetric equations of state): for instance, one can mention Fu et al. (1995), Mengarelli et al. (1999) and Chen et al. (2004), among others. Nevertheless, chemical theory is still an appealing theory, presenting ramifications such as the widely used ERAS model, conceived by Heintz et al. (1986), and the continuous thermodynamic equation of state develped by Browarzik (2004).

A theoretical aspect, viz. the fact that often the chemical equilibrium is calculated independently of the excess Gibbs energy model, justifies further work in this field. Strictly, the chemical equilibrium constant is related to the ratio of activities, which are calculated using an excess Gibbs energy equation. Other similar ratios, as the ratio of concentrations or volume fractions, are true equilibrium constants only in some special cases, i. e, when certain excess Gibbs energy models are applied. As Hofman (1990) pointed out, the thermodynamics of association depends on the thermodynamics of the multicomponent system, and the expression for the equilibrium constant is defined beforehand by the excess Gibbs energy model. This kind of discrepancy occurs mostly when cross-association reactions are considered – cf. Kretschmer and Wiebe (1954), Nath and Bender (1983) and Brandani and Evangelista (1984) – in which the solvation equilibrium is calculated by a ratio similar to that obtained for the self-association equilibrium constant.

The purpose of this work is to present a modification of the model by Brandani and Evangelista (1984). It consists of two parts: the model is altered by adopting ideas of Kretschmer and Wiebe (1954), and some assumptions from a previous development of an equation of state for self-association compounds (Pessoa Filho and Mohamed, 1999) are incorporated. No expression for the equilibrium constant is postulated ad hoc, in opposition to the way it is usually done in literature: the model herein developed uses the same UNIQUAC equation to calculate both the chemical equilibrium among the clusters and phase equilibrium. The extension of the model thus developed to cross-associating mixtures follows the ideas presented by Asprion et al. (2003). The model developed results in alternative expressions that provide good correlation of phase equilibrium in solutions involving self-association and solvation.

THEORETICAL DEVELOPMENT

When describing a mixture of an associating compound and some inert compounds, two different procedures are distinguished. One procedure neglects any association / solvation. The mixture consists of N components (e.g. A, D, ...). Its properties are designated by superscript (x), and the composition is characterized by stoichiometric amount fractions x_i, e.g. x_A, x_D, etc., whose sum equals one. The other procedure takes association / solvation into account. The mixture then consists of N_z > N species (e.g. A₁, A₂, A₃, ..., A_i+1, ..., D, ...), where A₁, A₂, A₃ represent monomers, dimers and trimers of component A and D is an inert, i.e. non-associating component). The properties are designated by superscript (z), but the composition is characterized by microscopic amount fractions z_i, e.g. etc., whose sum also equals one.

Self-Association Model

The development is based on a series of hypotheses concerning the occurrence of self-association and its relationship with the thermodynamic model. At first a mixture of a self-associating compound (A) and an inert one (D) is considered.

Based on stoichometric amount fractions, one obtains the following expressions for the chemical potential and the activity coefficient (normalized according to the Lewis and Randall rule) for component A:

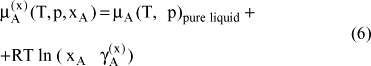
wherein x_A is the stoichometric amount fraction of component A, calculated through:

and and being the stoichiometric amount of components A and D, respectively. Analogous expressions hold for the inert component D.

• Hypothesis 1. The self-associating fluid is a mixture of clusters in chemical equilibrium according to equation (1) for i

  > 1.

The binary mixture of components A and D is therefore considered to be a multicomponent mixture of species, i.e. associates A₁, A₂, A₃, A₄, ... and the inert substance D. Based on microscopic amount fractions one gets for the chemical potential and the activity coefficient (normalized according to Lewis and Randall rule) for any species i:

where i stands for all species and z_i is the microscopic amount fraction of species i (i.e. A₁, A₂, ... or D):

The relative values of the equilibrium constants will be the subject of another hypothesis. The second hypothesis is concerned with the use of the UNIQUAC equation and its parameters.

• Hypothesis 2. The non-ideal behavior of the liquid phase is described by the UNIQUAC excess Gibbs energy model.

The activity coefficient of a substance (either component or species) i in a multicomponent mixture from the UNIQUAC equation is:

with

For the sake of simplicity, equation (11) is written without superscripts (either (x) or (z)) and with amount fraction y_i (instead of either x_i or z_i). is the number of nearest neighbors in the lattice (in this work, as usual, = 10).

The volume and surface parameters of a species (associate) A_i are given by:

where superscripts (x) and (z) have been omitted for the sake of simplicity. The binary parameters of the UNIQUAC model for interactions between interaction sites on an oligomer A_i and on an inert species D are assumed to be independent of the oligomer size:

The UNIQUAC parameters related to interactions between sites of any two oligomers A_i and A_j are null:

Expressions for the mixture terms present in the UNIQUAC equation can now be developed. As association / solvation results in a reduction of the total amount of substance, a parameter x is defined to describe that reduction. x is the ratio of 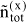, the macroscopic amount of substance, and 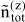, the microscopic amount of substance:

which leads to:

An average size parameter using 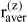the microscopic amount fractions z_i is defined:

as well as an average size parameter using stoichometric amount fractions (i.e. amount fractions x_A and x_D of components A and D):

Combining equation (20) with equations (21) and (22) results in:

The microscopic volume fractions and of a species (oligomer) A_j and of the inert species, respectively, in the mixture are:

and:

The volume fractions of the components A and D from the overall amount fractions x_A and x_D ( and ) are expressed similarly:

It can be noticed that the volume fraction of D is independent of the consideration or neglect of association. One can also express the volume fraction of component A on stoichometric amount fraction scale through the volume fractions of the oligomers on microscopic amount fraction scale:

Analogous expressions for averaged surface parameters and surface fracions can be obtained in exactly the same way.

Applying equation (11) to describe the activity coefficient of species i (i.e. on microscopic amount fraction basis) gives:

The denominator of the last term on the right hand side of this equation is:

As, from equations (16) to (18),t_Ai,Aj = 1, t_D,Aj = t_D,A and t_Aj,D, for an oligomer j º A_i one gets:

which does not depend on the number of monomer units in A_i, being henceforth refered to as S_A. For the species D, a similar procedure gives:

The sum apeearing in equation (29) can be rearranged to:

Inserting this equation as well as equation (12) for l_i, and introducing x from equation (23) and its analogous for the surface parameters into equation (29) results in the activity coefficient for the associating species:

In a very similar procedure the final expression for the activity coefficient of the inert species is:

The third hypothesis is concerned with the relative value of the chemical equilibrium constants.

• Hypothesis 3. Following Kretschmer and Wiebe (1954), it is assumed that the chemical reaction (1) is accompanied by a Gibbs energy change that is independent of i when ocurring between isolated molecules.

According to the definition of equilibrium constant:

wherein K_i+1 is the equilibrium constant for the formation of species A_i+1 according to equation (1) and the changes in Gibbs energy, enthalpy and entropy are related to the reaction occurring between pure liquid species. In order to analyze the dependency of K_i+1 on i, one must consider that, when the standard state is changed to the pure liquid species, there is an aditional entropy change due to differences in volumes per amount of substance. Since the volume of the oligomer is considered to be proportional to the number of monomers, one can write after Kretschmer and Wiebe (1954):

wherein DG⁰ does not depend on i. This expression leads to the following dependency of the equilibrium constant:

From equation (34), one recognizes that the activity of an oligomer A_i can be written as:

in which g is a function that does not depend on i. As the thermodynamic chemical equilibrium constant is:

one gets:

Setting K_e = exp(l + ln K) results in:

Equation (42) is a recursion formula that allows for the calculation of the amount fractions of the species A_i from the monomer amount fraction. Thus, only Z_A1 and x remain in fact to be determined.

There are two independent equations relating the two unknown variables: the definition of x, equation (19) and the sum of all amount fractions, equation (10). Details on the mathematic solution of the problem are presented in ^{appendix A}; the final expressions are:

and:

The value of z_D, which is necessary to calculate the activity of the inert compound, is obtained from equation (20). The model expressed by the set of equations (34), (35), (43) and (44) is referred to hereafter as the A-UNIQUAC model.

Cross-Association: Concepts and Equations

There are two ways to consider a chemical equilibrium between an active compound (e. g. an aromatic hydrocarbon) and an associating compound (e. g., an alcohol). One way is to consider that the hydrocarbon molecule may bond to any cluster regardless of its size – cf. Kretschmer and Wiebe (1954) and Nagata (1985). The other approach considers that the hydrocarbon molecule bonds only to a single cluster of solvent molecules, as in the treatment presented by Asprion et al. (2003) and, by analogy, Yu et al. (1993). The first approach introduces some mathematical difficulties which stand in the way of a rigorous solution of chemical equilibrium. The second is mathematically simpler and provides similar results; consequently, it was adopted to represent cross-association in the present work. One must be aware that it is not an exact representation of the molecular phenomenon: cross-association is accounted for only through its effect in correcting the abnormal departure from the ideal behavior caused by self-association rather than its molecular implications – for it would be impossible to take any possible electron donning reaction into account. This assumption is a break-even between mathematical feasibility and the correct description of the macroscopic effects of the microscopic phenomenon.

Thus, besides the self-association reactions considered earlier, a single cross-association reaction:

is considered to occur. The compound BA_j is regarded as an inert one, i. e, it will not undergo any other chemical reaction with other compounds.

The equilibrium constant for the reaction is K_AB:

This reaction causes changes in the mass balance. Therefore, a new parameter, the dimensionless extent of cross-association c is introduced. c is defined as the amount of B undergoing cross-association divided by the overall amount of substance in the solution:

The numerator of this equation can be substituted using the amount of the associating species, i. e, species containing only segments A₁, resulting in:

The values of c and K_AB are related to each other, as will be seen later. The following relations hold for the composition:

The value of Z_Ai is to be obtained through solving the chemical equilibrium.

In order to adapt the model, the second hypothesis, presented earlier, is extended: the pure compound UNIQUAC parameters for the new species are:

Also the hypothesis that the solvation does not modify the value of the interaction parameters for the inert compound is made, leading to a_BAj,Ai = a_B,A, a_Ai,BAj = a_A,B and a_B,BAj = a_BAj,B = a_BAj,BAj = a_B,B = a_Ai,Ak = 0. These expressions are obviously a simplification of the actual problem. In principle, it is possible to account for the differences between the distinct species using the definition of a_ij as the difference of interaction energies; however, it would complicate the subsequent development, and other simplifying assumptions would be necessary.

The definition of averaged values , , and remains the same, although the expressions of and are changed to account for the new species:

and similarly for . As before, the values and , and and are related through x, as given by equation (23) for the size parameters, for instance. Size and surface fractions are also calculated through the same expressions.

The activity coefficient takes different forms according to the compound to which it is related. In any case, the sum is written as:

For an oligomer A_i it becomes:

and for B and BA_j:

Substituting these expressions in equation (29), one gets for the activity coefficient of the oligomers:

and for B and BA_j:

where in m stands for either B or BA_j.

Again, the activity of the oligomers can be written as:

wherein g' is not a function of i. The use of the chemical equilibrium relationship, equation (40), leads to the same recursive equation (42). However, the procedure to z_A1 obtain and x is slightly different, as the mass balance has to be adapted. As shown in ^{appendix B}, it results in:

and:

With these expressions, the concentration Z_Ai, Z_B and Z_BAj, as well as the activity coefficient , and can be calculated when c is known. While the hypotheses made so far facilitated the mathematical manipulation of the equations, it is not possible to eliminate the need of a trial-and-error solution for c. One way to do so would be to substitute the expressions for the activity coefficients in equation (46) and solve it; however, as there are other equations being considered (the self-association ones), it is difficult to tell in advance whether the solution to be found is an actual stable solution. The other way is to minimize the Gibbs energy of the system.

Total Gibbs energy is given by:

The condition of equilibrium between the oligomers (µ_Ai = iµ_A1) leads to:

Introducing the concept of activity gives:

Using the definition of the extent of cross-association extent, the expression for G can be rewritten:

The standard chemical potentials in the above equation are related to the equilibrium constants through:

The amount of the species are related to c through equations (47) and (48). The term is constant for a given stoichometric composition, and has no influence in the minimization procedure. Therefore, c is found by minimizing the following expression for a given stoichometric composition (x_A and x_B) of a liquid mixture:

For the sake of simplicity, the modified model taking both self and cross-association into account is called AS-UNIQUAC.

Phase Equilibrium

The previous discussion was restricted to liquid phases. Applying those results in describing the vapor-liquid equilibrium requires some additional assumptions for the vapor phase. We assume that the vapor is an ideal gas of monomers A₁ and species D. When the pure liquids (i. e, A₁ and D) are chosen as the reference state, the conditions for vapor liquid equilibrium result in:

is the saturation pressure of a hypothetical liquid consisting of monomeric species A₁ only. is not directly accessible by experiment as it is not the saturation pressure above pure liquid component A (which is a mixture of monomers A₁ and associates A_n). is eliminated by considering the vapor liquid equilibrium of pure liquid component A:

wherein and are the amount fraction and the activity coefficient of monomers A₁ in pure liquid A. Introducing equation (70) into equation (68) gives:

The composition of the vapor and the pressure above a liquid mixture of an alcohol A and an inert component D of given stochiometric composition at temperature T is then calculated in several steps:

• Calculation of

  and

  in pure liquid A at temperature T.

• Calculation of amount fractions and z

  _D from equations (43), (44) and (20).

• Calculation of activity coefficients g

  _A1 and g

  _D from equations (34) and (35).

• Calculation of vapor phase fugacities y

  _AP and y

  _DP from equations (69) and (71).

If cross-association has to be accounted for, the procedure is similar, except for the fact that solvation equilibrium must be calculated prior to phase equilibrium, through solving the minimization problem, equation (67).

Obtaining the Parameters

The model requires three parameters to characterize an alcohol A: size parameter r_A, surface parameter q_A and the association equilibrium constant K , equation (38). We assume that K depends on temperature through:

A₀ and B₀ are obtained in a procedure adopted from Brandani (1983), using experimental data for the saturation pressure of the alcohol and the saturation pressure of an inert hydrocarbon having (nearly) the same molecular mass . The procedure consists of minimizing the following objective function:

For a binary mixture of an alcohol A and a neither associating nor cross-associating component D the model further requires two binary interaction parameters (a_AD and a_DA). These are obtained as usual by fitting binary vapor-liquid equilibrium data. In the present work the following objective function is used:

When cross-association between an inter species B and an associate A_j has to be taken into account, the chemical equilibrium constant K_AB , equation (46) has also to be determined from an extension of equation (74):

The dependency of K_AB on the temperature is written in the usual pattern for equilibrium constants:

The binary interaction parameters, regardless which equation they refer to, were considered to be independent of the temperature.

RESULTS

Self-Association

The equations previously developed were applied for the determination of the parameter A₀ and B₀ of equation (72) for five alcohols; these values are given in Table 1. Brandani (1983) also reported numerical values for A₀ and B₀, which are, for comparison purposes, also given in Table 1.The difference in the values of B₀ is small and is mainly due to the different range of temperature for which vapor pressure data were used. The difference in the value A₀ is larger, due to the distinct standard states chosen.

The model was subsequently used to calculate the vapor-liquid equilibrium of six binary systems of an alcohol and a paraffin at seventeen temperatures. The mean relative errors in the bubble point pressure calculated with A-UNIQUAC were compared to those obtained with the UNIQUAC Gibbs excess energy model (without taking association into account) in Table 2. The parameters of both equations are given in Table C-1 of ^{Appendix C}. The correlation with A-UNIQUAC always produced a better agreement with experimental data than obtained with the UNIQUAC. The relative difference in the bubble point pressure was reduced by a minimum of almost 20% (ethanol / methylcyclohexane system) and by a maximum factor of eight (for the ethanol / heptane system). The composition of the vapor phase calculated using the A-UNIQUAC equation is also closer to the experimental one (Table 2). When association was neglected, the correlation predicted a liquid-liquid phase separation, e. g., for the systems ethanol / hexane, ethanol / octane and 1-propanol / cyclohexane. Taking association into account avoided this false prediction and resulted in a better agreement with experimental data. As both A-UNIQUAC and UNIQUAC required two adjustable parameters, the improvement in correlation was a result of the explicit consideration of the self-association of the alcohol.

Solvation

In liquid mixtures of an alcohol and an aromatic hydrocarbon, such as benzene or toluene, the aromatic ring acts as an electron donor, and hydrogen bonding would occur between the aromatic ring and the alcohol. Although this cross-association is weaker than the self-association of an alcohol, it would also need to be considered in Gibbs excess energy models.

In the present work solvation between an alcohol and benzene or toluene was taken into account as discussed before. As the chemical constant for the reaction could not be estimated from pure component data, it had to be introduced as a third adjustable parameter. An alternative way to take self-association into account was given by Kretschmer and Wiebe (1954) for the system ethanol / toluene. As cross-association reduces self-association, Kretschmer and Wiebe used for the chemical equilibrium constant for the self-association of ethanol in toluene a much smaller value than for ethanol in an inert hydrocarbon.

The AS-UNIQUAC model was applied to fit VLE data of four mixtures of an alcohol (ethanol, 1-propanol, 1-butanol) with benzene or toluene at eleven temperatures. As benzene and toluene have only a single electron donor site, only cross-association between one aromatic ring and one alcohol molecule or oligomer was expected. The influence of temperature on cross-association was described by equation (76). Thus, when temperature varies, the AS-UNIQUAC model has four adjustable parameters, plus the average number of the oligomer cross-associated.

The parameters were obtained by fitting the bubble point pressure data of the four binary systems. As the parameter j can assume only integer values, it was varied independently; in all cases studied, the optimum value was found to be one. These parameters are given in Table C-2 of ^{appendix C}. The relative mean deviation between calculated and experimental values for the bubble point pressure and the absolute mean deviation in the vapor phase composition are given in Table 3. The parameter B₁ of equation (76) for the cross-association is always smaller than the same parameter for the self-association of an alcohol, as can be seen in Table 4. As B is directly related to the association enthalpy, this finding is in agreement with the expectation that the absolute value for the self-association enthalpy should be larger than the absolute value for the cross-association enthalpy.

Table 3 also gives a comparison of the results obtained when correlating the bubble point pressure data using UNIQUAC (i. e, without any association) to those obtained using A-UNIQUAC (i. e, with self-association only) and AS-UNIQUAC. As expected, AS-UNIQUAC gives the best agreement with the experimental data. However, in this case the improvement is not as remarkable as for alcohol / paraffin mixtures, as the UNIQUAC equation already results in reasonable accuracy. Taking self-association into account, but neglecting cross-association (i. e, using A-UNIQUAC) results in comparatively large deviations between the calculated and the experimental data.

Figure 1 shows the extent of the cross-association reaction c as a function of concentration for the 1-propanol / benzene system at two different temperature. In this figure, the value of c / x_B (i. e, the fraction of hydrocarbon molecules that undergo solvation) is plotted versus x_A (the stoichometric amount fraction of the alcohol). It can be verified that the extent of cross-association is not large: while neglecting it worsens significantly the correlation, its low value may be the responsible for the fact that only one alcohol molecule is calculated to be associated to each electron-donor site. The extent of cross-association increases with increasing amount fraction of the alcohol, passes through a maximum and decreases to a nearly concentration independent number that increases with increasing temperature. This is the result of two counteracting effects: at higher temperatures there is a lower extent of self-association (i. e, a higher amount fraction of alcohol monomers, Figure 2), which leads to a higher extent of solvation. This higher extent overcompensates the otherwise reducing effect of temperature on solvation. Accounting for concurrent reactions also explain the existence of a maximum for c / x_B at lower alcohol amount fractions, as can be verified in Figure 3 the total fraction of self-association f_A, defined as the ratio of the calculated number of hydrogen bonds to the maximum allowed, is presented for the same system: both self- and cross-association reactions experience an steep increase for lower concentrations of alcohol.

CONCLUSIONS

The effect of linear chain self-association and solvation was incorporated into the UNIQUAC model for Gibbs energy in a straightforward way, without postulating any expression for the equilibrium constant, but using instead the activity of the oligomers as they are obtained from the UNIQUAC equation to calculate the chemical equilibrium. The pure self-association model thus developed presented good results for the correlation of VLE data of alcohol / alkane mixtures, being able to correlate systems at various temperatures within experimental uncertainty. For systems containing an alcohol and an aromatic hydrocarbon a cross-association reaction was considered; it was found that the correlation was also excelent in this case, with low deviations from experimental data, notwithstanding the fact that the extent of cross-association was calculated to be small.

NOMENCLATURA

Latin Letters

A

monomer of a self-associating component

A₀, A₁

parameters in the equation of the equilibrium constant

A_i

oligomer of i monomors of A, i = 1, 2, ....

a_i,j

binary UNIQUAC interaction parameter between sites of component i and j.

B active compound B₀, B₁

parameters in the equation of the equilibrium constant

c_i concentration of species i (amount of substance per volume)

D

inert compound

e

2.7182818...

f_A

dimensionless extent of self-association

g

function defined by equation (39)

G

Gibbs energy [J.mol^-1]

G

total Gibbs energy of a sample [J]

H

enthalpy [J.mol^-1]

i

number of monomers in a multimer

j

number of monomers in a multimer

K_AB

equilibrium constant of solvation reaction

K_i

chemical reaction equilibrium constant for the formation of A_i; i = 2, 3, 4...

l_j

parameter in the UNIQUAC equation definedy by equation (12)

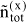
total amount of components [mol]

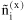
overall amount of component i [mol]

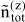
or microscopic amount of compounds [mol]

microscopic total amount of species i [mol]

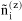
N

number of components

N_z

number of species

P

pressure [Pa]

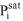
saturation pressure of species i [Pa]

q

surface parameter of the UNIQUAC equation

average surface parameter on stoichometric amount fraction basis average surface parameter on microscopic amount fraction basis R universal gas constant [8.314 J.mol^-1.K^-1] r size parameter of the UNIQUAC equation average size parameter on stoichometric amount fraction basis average size parameter on microscopic amount fraction basis S entopy [J.mol^-1.K^-1] S_i paramenter in the UNIQUAC equation defined by equation (30) T thermodynamic temperature [K] V volume per amount of substance [L.mol^-1] x_i stoichiometric amount fraction of component i y_i amount fraction of component i in the vapor phase z_i or microscopic amount fraction of species i number of nearest neighbors in the lattice Greek Letters a_i activity of component i c dimensionless extent of reaction, defined by equation (47) x = g_i activity coefficient of component i q_i surface fraction of component i j_i volume fraction of compenent i µ_i chemicla potential of component i [J.mol^-1] t_ij exp(-a_ij / T) Subscripts aver average A monomer of self-associating component A_i oligomer species consisting of i monomors of component A; i = 1, ..., ¥ D inert component or inert species s solvation tot total Superscripts c based on concentration calc calculated E excess exp experimental L liquid sat saturation x stoichiometric z microscopic 0 standard j based on volume fraction

*

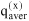
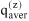
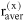
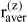
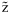
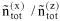
pure alcohol

Received: July 6, 2004

Accepted: March 15, 2005

Applying the recursive formula, equation (42), gives:

from which one obtains:

and:

From equation (20):

and:

Relating equations (A2) to (A5), and (A3) to (A4), one obtains a set of two equations with the unknown z_A1 and x:

Dividing the square of equation (A6) by equation (A7), and recalling that x_A = 1 - x_D, gives:

The expression for x is obtained by inserting equation (A8) into equation (A6). After some rearrangement, one gets:

which is a quadratic equation that can be solved by means of usual algebra. The only meaningful solution is obtained by considering that for x_A = 0, x_D = 1 and x = 1:

In order to avoid numerical problems when Ke ® 0 and the self-association vanishes, rearrangement is made resulting in equation (44). With some variations, this form of equation is usually found in chemical-theory based models.

The procedure to be followed to obtain Z_A1 and x when both self and cross-association are considered is slightly different from that presented in ^{appendix A}. Equations (A1) to (A3) remain the same, but their relation with overall quantities is changed. In this case, from equations (10), (49) and (50):

From equations (19) and (48):

From equations (A2) and (B1):

From equations (A3) and (B2):

After similar rearrangement:

In order to obtain the value of x, equations (B1) and (B5) are substituted in equation (A2), leading to:

whose only meaningful solution is equation (61).

• Asprion, N., Hasse, H. and Maurer, G., Thermodynamic and IR Spectroscopic Studies of Solutions with Simultaneous Association and Solvation, Fluid Phase Equilibria, 208, 23 (2003).
• Brandani, V., A Continuous Linear Association Model for Determining the Enthalpy of Hydrogen-Bond Formation and the Equilibrium Association Constant for Pure Hydrogen-Bonded Liquids, Fluid Phase Equilibria, 12, 87 (1983).
• Brandani, V., and Evangelista, F., The UNIQUAC Associated-Solution Theory: Vapor-Liquid Equilibria of Binary Systems Containing one Associating and one Inert or Active Component, Fluid Phase Equilibria, 17, 281 (1984).
• Chen, J., Mi, J. G., Yu, Y. M., and Luo, G. S., An Analytical Equation of State for Water and Alkanols, Chem. Eng. Sci., 59, 5831 (2004).
• Browarzik, D., Phase-equilibrium Calculations for n-Alkane plus Alkanol Systems Using Continuous Thermodynamics, Fluid Phase Equilibria, 217, 125 (2004).
• Flory, P. J., Thermodynamics of High Polymer Solutions, J. Chem. Phys., 10, 51 (1942).
• Fu, Y. H., Sandler, S. I., and Orbey, H., A Modified UNIQUAC Model that Includes Hydrogen Bonding, Ind. Eng. Chem. Res., 34, 4351 (1995).
• Gmehling, J. and Onken, U., Vapor-Liquid Equilibrium Data Collection, Chemistry Data Series, v. 1, part 2a. Dechema, Dortmund (1977).
• Gmehling, J., Onken, U. and Arlt, W., Vapor-Liquid Equilibrium Data Collection, Chemistry Data Series, v. 1, part 2c. Dechema, Dortmund, (1982a).
• Gmehling, J., Onken, U. and Weidlich, U., Vapor-Liquid Equilibrium Data Collection, Chemistry Data Series, v. 1, part 2d. Dechema, Dortmund (1982b).
• Heintz, A., Dolch, E. and Lichtenthaler, M., New Experimental VLE-Data for Alkanol-Alkane Mixtures and their Description by an Extended Real Association (ERAS) Model, Fluid Phase Equilibria, 27, 61 (1986).
• Hofman, T., Thermodynamics of Association of Pure Alcohols, Fluid Phase Equilibria, 55, 39 (1990).
• Kempter, H. and Mecke, R., Spektroskopicsche Bestimmung von Assoziations-Gleichgewitchen, Z. Phys. Chem., B46, 229 (1940).
• Kretschmer, C. B. and Wiebe, R., Thermodynamics of Alcohol-Hydrocarbon Mixtures, J. Chem. Phys., 22, 1697 (1954).
• Mengarelli, A. C., Brignole, E. A. and Bottini, S. B., Activity Coefficients of Associating Mixtures by Group Contribution, Fluid Phase Equilibria, 163, 195 (1999).
• Nagata, I., On The Thermodynamics of Alcohol Solutions. Phase Equilibria of Binary And Ternary Mixtures Containing Any Number of Alcohols, Fluid Phase Equilibria, 19, 153 (1985).
• Nagata, I., Kawamura, Y., Excess Thermodynamic Functions of Solutions of Alcohols with Saturated-Hydrocarbons - Application of UNIQUAC Equation to Associated Solution Theory, Z. Phys. Chem. Neue Folge 107, 141 (1977).
• Nath, A. and Bender, E., On the Thermodynamics of Associated Solutions. I. An Analytical Method for Determining the Enthalpy and Entropy of Association and Equilibrium Constant for Pure Liquid Substances, Fluid Phase Equilibria, 7, 275 (1981a).
• Nath, A. and Bender, E., On the Thermodynamics of Associated Solutions. II. Vapor-Liquid Equilibria of Binary Systems with one Associating Component, Fluid Phase Equilibria, 7, 289 (1981b).
• Nath, A. and Bender, E., On the Thermodynamics of Associated Solutions. III. Vapor-Liquid Equilibria of Binary and Ternary Systems with Any Number of Associating Components, Fluid Phase Equilibria, 10, 43 (1983).
• Pessôa Filho, P. A. and Mohamed, R. S., A Chemical Theory Based Equation of State for Self-Associating Compounds, Thermochimica Acta 328, 65 (1999).
• Renon, H. and Prausnitz, J. .M., On the Thermodynamics of Alcohol-Hydrocarbon Solutions, Chem. Eng. Sci., 22, 299 (1967).
• Smith, B. D. and Srivastava, R. Thermodynamic Data for Pure Compounds, Part B: Halogenated Hydrocarbons and Alcohols. Elsevier, Amsterdam (1986b).
• Smith, B. D. and Srivastava, R., Thermodynamic Data for Pure Compounds, Part A: Hydrocarbons and Ketones. Elsevier, Amsterdam (1986a).
• Yu, M., Nishiumi, H. and Arons, J. S., Thermodynamics of Phase Separation in Aqueous Solutions of Polymers, Fluid Phase Equilibria, 83, 357 (1993).

APPENDIX A 

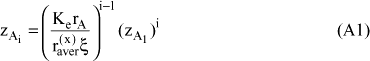
APPENDIX B 

APPENDIX C 

*

To whom correspondence should be addressed

†

This paper is dedicated to the memory of Prof. Dr.R.S.Mohamed, who passed away after finishing this work.

Publication Dates

• Publication in this collection
  28 Sept 2005
• Date of issue
  Sept 2005

History

• Accepted
  15 Mar 2005
• Received
  06 July 2004