An exactly soluble multiatom-multiphoton coupling model

REGULAR ARTICLES

An exactly soluble multiatom-multiphoton coupling model

A. N. F. Aleixo^I; A. B. Balantekin^II; M. A. Cândido Ribeiro^III

^IInstituto de Física, Universidade Federal do Rio de Janeiro, Rio de Janeiro, RJ Brazil

^IIDepartment of Physics, University of Wisconsin, Madison, Wisconsin 53706 USA

^IIIDepartamento de Física, Instituto de Biociências, Letras e Ciências Exatas, UNESP, São José do Rio Preto, SP, Brazil

ABSTRACT

A class of bound-state problems which represent the interaction between a system of N two-level atoms and an electromagnetic radiation via an m-photon process is studied, with m = 1; 2; 3;.... We also evaluate some nonlinear effects usually related with the polarisability of the medium and with the dependence on the intensity of the radiation field on the matter-radiation interaction. We obtain exact values for the eigenstates and eigenvalues for all values of total angular momentum of the system and all possible number m of photons involved in the interaction. We give explicit analytic expressions for small numbers of atoms and discuss some aspects of the composition of the eigenstates and of the spectra obtained in these cases.

1 Introduction

A standard model most used in quantum optics idealizes the interaction of the matter with the radiation by a simple Hamiltonian of a two-level atom coupled to a single bosonic mode [1]. This Hamiltonian is a central ingredient in the quantized description of any optical system involving the interaction between light and atoms. For this Hamiltonian, mostly the single-particle situation has been studied [2-13]. The purpose of this paper is to give the exact and complete solution for this model when we consider the presence of N two-level systems which interact with a single-mode radiation via a single or multi-photon process, that take place when the energy separation between the atomic levels is close to the energy of m radiation quanta. In this case the effects of the spatial distribution of the particles it is not taken into account and the spin angular momentum _i of each particle contributes to form a total angular momentum of the system. We consider in this study the effects due to the nonlinear radiation polarisability with the inclusion of a nonlinear term in the Hamiltonian [8]. This kind of nonlinear effect is usually considered in the study of micromasers.

Another nonlinear extension of our study takes the coupling between matter and the radiation to depend on the intensity of the radiation field [4-6,9]. It is interesting since this kind of interaction means that effectively the coupling is proportional to the amplitude of the field, corresponding to a more realistic physical situation. We obtain exact values for the eigenstates and eigenvalues for all values of j and for any number m of photon involved in the atom-radiation interaction. We give explicit analytic expressions for small numbers of atoms and discuss some aspects of the spectra obtained in these cases.

This paper is organized in the following way, in Section II we introduce the multiatom Hamiltonian with multiphoton interaction and its solution; in Section III we do the same for an intensity-dependent radiation interaction; application are presented in Section IV and some numerical results with its discussion are presented in section V. Finally, conclusion and brief remarks close the paper in Section VI.

2 Multi-atom model with multi-photon interaction

The Hamiltonian describing the interaction between a single-mode radiation and N two-level systems via an m-photon process, when we include nonlinear effects, can be written as

with m = 1,2,3,...,

Here W is the matter-radiation interaction parameter, Q is the nonlinear medium parameter, related to the third-order nonlinear susceptibility, D_m = mw - w₀ is a constant related to the detuning of the system and w (w₀) is the field (atomic transition) frequency. In the above expressions,

where

_i (with i = 1, 2, and 3) are the components of the total angular momentum of the system, obtained by the sum of the spin angular momentum of the N two-level atoms.

To obtain the eigenstates and eigenvalues for the Hamiltonian (2.1) we first remember that the bosonic operators, when applied to the number states, satisfy the following properties

where the excited bosonic states are written as

Now, if we introduce the operators

and

that satisfy the following commutation relations

and

where

then we can rewrite the components of the total Hamiltonian (2.1) as

Note that for m = 1 the new operators reproduce the standard bosonic commutation relations [,â] = -â, [,â^†] = â^†, [â,â^†] = 1, characteristic of the Heisenberg-Weyl algebra, and for m = 2 these commutation relations, which can be written as [₂, Â₂] = -Â₂, [₂, ] = , and [Â₂, ] = 2₂, represent the bosonic realization of the SU(1,1) algebra.

With the new form (2.9) of the total Hamiltonian elements it is easy to show that the two terms in the Hamiltonian (2.1) commute with each other, [(0),⁽¹⁾] = 0, therefore it is possible to find a common set of eigenstates for them. The simplest way to determine the eigenstates and eigenvalues of that Hamiltonian is by calculating the eigenstates and eigenvalues of ⁽¹⁾. Taking into account that the _i operators can be represented by (2j + 1) × (2j + 1) matrices, then by using the form of these matrices we can write the operator ⁽¹⁾ as a tridiagonal matrix with these same dimensions of _i and whose elements can be written as

with the property = ()^†. By considering the properties (2.4) of the bosonic operators and the matrix form of the operator (1), we introduce the following vector for its eigenstates

where the C coefficients are to be determined by the eigenvalue equation

which also determines the eigenvalues

_nm. Basically the vector |Y_nmñ corresponds to the state of the system with total angular momentum J² = j(j + 1)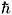² and each vector component represents one of 2j + 1 possible values of J_z. In other words, the component |n + kmñ of the vector state |Y_nmñ represents the quantum state {n, j, m_j = j - k}. By considering that m|kñ = 0 if k < m and

and also

then, by substituting Eqs. (2.10) and (2.11) into Eq. (2.12) we obtain the set of (2j + 1) coupled algebraic equations which can be written in a compact form as

where k = 1,2,3,...,2j + 1 and the h-coefficients are defined as

With this set of (2j + 1) equations plus the normalization condition for the eigenstate it is possible to obtain the (2j + 2) variables that appear in (2.15). This set of equations can be written in a matrix form as

where the tridiagonal h-matrix has its elements given by Eq. (2.16) with the symmetry condition h_ki = h_ik and being C the column matrix

The secular equation associated to Eq. (2.17) gives us the algebraic equation to calculate the 2j + 1 possible values for the eigenvalues _nm

where the D coefficients are related to the h-matrix elements. Finally, by using Eqs. (2.1), (2.11) and (2.12) we have

So far we have only discussed about the possibility of having n > 0. By considering that n corresponds to the smallest number of photons we might measure in the vector state |Y_nmñ, then when n > 0, it means that we can find all values of m_j from -j to j. Therefore when we have -2j < n < 0 the vector state |Y_nmñ corresponds to states in which there are not enough photons to excite the higher m_j values even if all of them are absorbed. In this case, the vector state (2.11) that represents this situation will be written as

where -2j < r < 0. In particular, the case r = -2j, that corresponds to the vacuum combined with all particles in their lowest state, represents the ground state of the system. The determination of the eigenstates and eigenvalues of the Hamiltonian (2.1) for these 2j possible n negative values corresponds to a particular application of the general treatment presented before and it will be studied and analyzed for each particular j value in the applications below.

3 Multi-atom model with intensity-dependent multi-photon interaction

We now introduce an intensity-dependent interaction between matter, constituted by N two-level particles, and radiation via an m-photon process by using the following form for the interaction Hamiltonian

where the new operators are defined as

and

The other terms in the total Hamiltonian (2.1) keep the same forms as used in the previous Section. These facts imply that the diagonal elements of the total Hamiltonian are still given by Eq. (2.10) and the non diagonal matrix elements now are written as

with i,k = 1,2,3,...,2j + 1 , and with the property ki = . Again, those both terms, ₀ and ₁, in the total Hamiltonian (2.1) commute with each other. Therefore, it is possible to use the same technique as used in the preceding Section to obtain the eigenstates and eigenvalues for the total Hamiltonian. Now, by considering that _m|kñ = 0 if k < m and

and also

then using Eqs. (3.3) and (2.11) into Eq. (2.12) we obtain a new set of (2j + 1) coupled algebraic equations which can be written in a compact form as

where k = 1,2,3,...,2j + 1 and the new 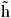_{i k} coefficients, with i ¹ k, are related with the previous one (h_{i k}) by

and the symmetry property

_{i k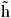} = _{k i}. The diagonal h_kk coefficients remain given by Eq. (2.16). Again, the above set of equations can be written in a matrix form as given by Eq. (2.17), except that the non diagonal matrix elements of h appear now substituted by these 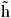_{i k} new elements. In this case, to have the spectra we need to resolve Eq. (2.19), where the D coefficients take into account the changes in Eq. (3.6).

It is important to note that the inclusion of negative values of n for this case can be done in the same way as indicated in the previous Section. However, in contrast with what we have for the previous case, the effects of the intensity dependence on the eigenstates and eigenvalues for n negative values will only be observed for j > 1.

4 Applications

A. Single-particle system

In this case j = 1/2 and the Hamiltonian (1) will be a 2 × 2 matrix. Applying this Hamiltonian to the eigenstate equation (2.12), we obtain the matrix equation (2.17) with

being the h_ik coefficients given by Eq. (2.16). Then the system of equations (2.15) becomes

and, from Eq. (2.19), we have an algebraic quadratic equation with coefficients D₁ = -(h₁₁ + h₂₂) and D₀ = h₁₁h₂₂- for the eigenvalues which will be given by

From Eqs. (4.3), (4.2) and the eigenstate normalization condition we can determine the C coefficients and show that the eigenstates for the total Hamiltonian can be written as

with n = 0,1,2, ... , m = 1,2,3, ... , where

with eigenvalues given by

For the case of intensity-dependent interaction, we obtain (with the change h_ik® 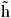_ik, i ¹ k), the following eigenvalues of ⁽¹⁾

while the eigenstates for the total Hamiltonian can be written in the same form given by Esq. (4.4) and (4.5), but with

The eigenvalues for the total intensity-dependent Hamiltonian will be written as in Eq. (4.6) but, now, with given by Eq. (4.7). These results can be reduced to the standard model and to the intensity dependent interaction standard model results [13,14] when we assume the value m = 1 and turn off the nonlinearity term taking Q = 0.

For j = 1/2 the only possible negative n value is r = -2j = -1 that corresponds to the ground state of the system. Considering this fact and using Eqs. (2.21), (4.1) and (4.2) it is easy to show that

In the case of the intensity dependent interaction we have these same results for the eigenvalues and eigenstates as written in Eqs. (4.9).

B. Three-particle system

In this case we can have j = 1/2 or j = 3/2. We have already studied the first possibility. For the second j value, the Hamiltonian (1) is a 4 × 4 matrix that applying to the eigenstate equation (2.12), give us the matrix equation (2.17) with

being the h_ik coefficients given by Eq. (2.16). Then the system of equations (2.15) becomes

and Eq. (2.19) is an algebraic quartic equation with coefficients

and the eigenvalues can be obtained by its roots, as shown in Appendix II. From Eqs. (6.8), (4.11), (2.20) and the eigenstate normalization condition we can determine the C coefficients and show that the eigenstates for the total Hamiltonian can be written as

where

with k = 1,2,3,4 and

and its associated eigenvalues can be written as

Again, the results for the intensity-dependent interaction are obtained with the change h_ik® 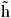_ik, with i ¹ k. Basically this change implies in a modification in the D₀, D₁ and D₂ coefficients of the algebraic quartic equation for the eigenvalues and in the G-terms for the eigenstates.

For this value of j, the possible n negative values are r = -2j + 2 = -1, r = -2j + 1 = -2 and r = -2j = -3, the last one being the ground state of the system. First, using Eqs. (2.21) and (4.10) for r = -1, we find the following system of equations

and from Eq. (2.19) we have an algebraic cubic equation with coefficients

for the eigenvalues , that can be obtained by using the recipe presented in Appendix I. From Eqs. (4.17), the normalization condition and with the eigenvalues we can calculate the C coefficients and show that the eigenstates for the total Hamiltonian in this case can be written as

where

with k = 1,2,3 and the eigenvalues given by

The modifications required to get the results for intensity dependent interaction case can be reduced to the change of the factors by and by in Eqs. (4.17), (4.18) and (4.20). For the case of r = -2, after taking the same procedure used before, we find the following system of equations

giving for the coefficients of the algebraic quadratic equation for the eigenvalues (2.19)

So, we find

Again, from Eqs. (4.24), (4.22) and the eigenstates normalization condition we can determine the C coefficients and show that the eigenstates for the total Hamiltonian for this case can be written as

where

and

being its eigenvalues given by

Now, the results for the intensity dependent interaction case can be obtained with the change of the factor by in Eqs. (4.22), (4.23), (4.24) and (4.26). Finally, using Eqs. (2.21), (4.10) and (4.11) for r = -3, we find

with

and

For this last case we do not observe the effects of the intensity dependent interaction on the results for the eigenstates and eigenvalues of the total Hamiltonian.

After these applications we emphasize that is just a matter of simple numerical work to find the eigenstates and the energy spectra, for any higher value of j. It is straightforward to do an analytical calculation up to five particle system, j_max = 5/2, when we have a resonant situation (D_m = 0) and we do not consider the presence of the nonlinearity term (Q = 0).

5 Numerical results and discussion

In this section we show some examples of exact numerical applications of the formalism developed in the previous sections.

In tables 1 and 2 we show the results for energy eigenvalues, E_nm, for the cases of one-particle and three-particle systems; j = 1/2 and j = 1/2, 3/2, respectively. The energies E_nm are given in units of 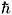w. The used values of the constants W, Q and D_m are chosen in a such way that the model approximation is preserved. The bosonic quantum number, n, is chosen as -2j < n < 2 and number of photons taking part in each process as m = 1, 2,3. Results in bold face stand for the intensity-dependent interaction case, otherwise for non intensity-dependent one. As shown in the tables, for all values of m, the number of levels increases from 1 to 2j + 1, as n goes from -2j to n = 2. Since the ground-state is a photon free state, the results for the intensity-dependent and non intensity-dependent cases for the ground states are equal for each value of m. For each value of j, the first excited state for m = 1 (labeled by n = -2j + 1), also has a same value for the intensity-dependent and non intensity-dependent situations. However, now this is because of the dependence on n and m shown by the eigenvalues, nm. For each value of j, as m increases the splitting among energy levels also increases. This effect is stressed in the case of intensity-dependent interaction.

Figure (1a) shows the behavior of the energy level diagram of the system for m = 1 and j = 1/2 with the energies given in units of 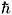w. In this figure we can see the split of the energy levels when we gradually turn on each component of the total Hamiltonian , process that is represented by the columns (A), (B), (C), and (D). The column (A) shows only the contribution of the radiation for the energy of the system since that the other components of the total Hamiltonian are turned off. The column (B) shows the symmetric splitting in the original energy levels caused by the inclusion of the matter-radiation interaction with a strength parameter W = 0.3 w. The column (C) shows the effects of the inclusion of the nonlinear term with a strength parameter Q = 0.2w in the total Hamiltonian. We can see that the net effect in this case is a shifting up and the increasing of the energy gap between the primary shifted levels when n > -2j + 2. Finally, the last column (D) presents the increasing of the energy gap between the primary shifted energy levels when we turn on the detuning of the system with D₁ = 0.2w. Note that the ground state energy is only modified by the presence of the nonresonant term, 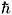D₁3, in the total Hamiltonian. This is because the ground state is a no photon state. It is important to note that for j = 1/2 case the introduction of the nonlinear term in the Hamiltonian does not affect the results for n negative values. This is because this nonlinear term takes into account a change of two photons and, thus, it is necessary to have eigenstates corresponding to bosonic states components |kñ with k > 2. Only for higher j values we can observe the effects of the nonlinearity on the eigenstates and eigenvalues for n negatives values. Figure (1b) is the intensity-dependent radiation version of Fig. (1a). If we compare these figures we conclude that the action of the intensity-dependence in the matter-radiation interaction is to generate an amplification in the energy gap of the levels which are sensitive to this dependence (n > -2j + 2).

Figures (2a) and (2b) are the version of Figs. (1a) and (1b) for m = 1 and j = 3/2, recpectively. We observe the same behavior presented for j = 1/2 case in the splitting of the energy levels when we turn on each component of the Hamiltonian, except for the splited energy levels number and the increasing in the energy gap between the levels.

Figure (3a) shows the behavior of the energy level diagram of the system for j = 3/2, n = 2 and m = 1,2,3; with energies given in units of 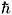w. In this Figure we can see the split of the energy levels when we gradually turn on each component of the total Hamiltonian , process that is represented by columns (A), (B), (C) and (D). The leftmost column (A) shows only the contribution of the radiation for the energy of the system since the other components of the total Hamiltonian are turned off. The next column (B) shows the symmetric splitting in the original energy levels caused by the inclusion of the matter-radiation interaction with a strength parameter W = 0.3w. The third column (C) shows the effects of the inclusion of the nonlinear term with a strength parameter Q = 0.2w in the total Hamiltonian. We can see that the net effect in this case is a shifting up and the increasing of the energy gap between the primary shifted levels. The last column (D) presents the increasing of the energy gap between the primary shifted energy levels when we turn on the detuning of the system with D_m = 0.2w. Finally, we note that as m increases, the gap between levels also increases. This kind of behavior of the energy levels is present for all excited states.

Figure (3b) is the intensity-dependent version of Fig. (3a). If we compare these two set of figures we conclude that the action of the intensity-dependence in the matter-radiation interaction is to generate an amplification in the energy gap of the levels.

Figure (4) shows the weight of each component, P_n+km = , with k = 0, 1, 2 and 3, in the composition of the state vectors, |ñ for j = 3/2, and n = m = 2. The values of parameters W, Q and D_m are the same as in the tables 1 and 2. In this Figure are shown the 2j + 1 states, from the less energetic state in the top to the more one in the bottom and the size of the vertical bars are proportional to the weight of the correspondent component. The column to the left is for the non intensity-dependent situation and that one to the right is for the intensity-dependent case. Clearly, in the non intensity-dependent situation and for the lowest energy eigenvalue (in the top), the components more important in the composition of the eigenstate correspond to the lower bosonic states. As the energy eigenvalue increases (going down in the figure), this behavior gradually change, in a such way that for the highest energy eigenvalue (in the bottom) we observe that the components with more importance in the composition of the eigenstate correspond to the higher bosonic states. For the intensity-dependent situation and for the positive energy eigenvalues, we observe the same behavior as describe above for the relative importance of the components in the composition of the eigenstate. However, for the only one eigenstate with a negative energy eigenvalue (in the top), we see that intermediate components present a higher relative importance than the components in the extremes. A non observed vertical bar in the figures does not mean that the respective component is null, but only that in the figure scale its relative value can not be represented.

Figure (5) is the same as for Figure (4) with n = m = 3. As we can see, for negative (top of each column) and positive energy eigenvalues, the general behavior for the relative importance of the components is the same as describe before.

6 Conclusions

In this article we introduced a model for interaction between the matter, consisting of N two-level particles, and the radiation via an m-photon process, with m = 1,2,3,.... The model includes the nonlinear effects related with the nonlinear polarisability in a nonlinear medium and nonlinear effects due an intensity-dependent radiation coupling. We present the exact results for the eigenstates and eigenvalues for some different values of j in terms of the photon number m. We compare the different spectra to evaluate the effects of the photon number involved in the interaction and the different sources of nonlinearity and also discuss some aspects of the composition of the eigenstates and of the spectra obtained in these cases.

We emphasize that our general model makes possible to resolve simultaneously problems with different Hamiltonians; as we set Q = D_m = 0, our model reduces to a bare resonant model for a multi-atom system interacting with an electromagnetic radiation via a multi-photon process; if we put Q = 0, D_m ¹ 0, we get a bare multi-atom -photon non resonant model and if we set Q ¹ 0, D_m = 0, we have a multi-atom -photon resonant model with a nonlinearity. We showed that it is straightforward to generalize all these situations for an intensity-dependent interaction.

A related quantum mechanical model for the propagation of light through a nonlinear medium taking into account the nonlinear polarisability of radiation was presented in Ref. [15]. Our Hamiltonian can be considered a generalization of this model. Indeed, for m = 1, using the Holstein-Primakoff boson mapping of the angular momentum algebra:

and introducing the scaled matter-radiation interaction parameter

one sees that in the limit j ® ¥, substitution of Eq. (6.1) into Eqs. (2.1), (2.1), (2.2) yields the Hamiltonian

up to a constant. Eq. (6.3) is the Hamiltonian studied in Ref. [15]. Our Hamiltonian can also be considered as an exactly-solvable coupled-channels problem. As many interesting problems in areas ranging from nuclear physics [16] to the study of transitions from metastable states [17] have coupled-channels form, our Hamiltonian can be a starting point for other models.

Acknowledgments

This work was supported in part by the U.S. National Science Foundation Grants No. INT-0070889 and PHY-0070161 at the University of Wisconsin, and in part by the University of Wisconsin Research Committee with funds granted by the Wisconsin Alumni Research Foundation. M.A.C.R. acknowledges the support of Fundacão de Amparo à Pesquisa do Estado de São Paulo - FAPESP (Contract No. 98/13722-2). A.N.F.A. and M.A.C.R. acknowledge the support of Conselho Nacional de Pesquisa (CNPq) (Contract No. 910040/99-0). A.N.F.A. and M.A.C.R. thank to the Nuclear Theory Group at University of Wisconsin for their very kind hospitality.

References

[1] E. T. Jaynes and F. W. Cummings, Proc. IEEE 51, 89 (1963).

[2] B. Buck and C. V. Sukumar, Phys. Lett. A 81, 132 (1981).

[3] C. C. Gerry, Phys. Rev. A 37, 2683 (1988).

[4] M. Chaichian, D. Ellinas, and P. Kulish, Phys. Rev. Lett. 65, 980 (1990).

[5] B. Deb and D. S. Ray, Phys. Rev. A 48, 3191 (1993).

[6] V. Buzek, Phys. Rev. A 39, 3196 (1989).

[7] W. R. Mallory, Phys. Rev. 188, 1976 (1969); I. R. Senitzky, Phys. Rev. A 3, 421 (1971).

[8] P. D. Drummond and D. F. Walls, J. Phys. A 13, 725 (1980).

[9] A. Rybin, G. Miroshnichenko, I. Vadeiko, and J. Timonen, J. Phys. A: Math. Gen. 32, 8739 (1999).

[10] C. Flytzanis and C. L. Tang, Phys. Rev. Lett. 45, 441 (1980).

[11] N. Imoto, H. A. Haus, and Y. Yamamoto, Phys. Rev. A 32, 2287 (1985).

[12] A. N. Aleixo, A. B. Balantekin, and M. A. Cândido Ribeiro, J. Phys. A 33, 3173 (2000) [quant-ph/0001049].

[13] A. N. Aleixo, A. B. Balantekin, and M. A. Cândido Ribeiro, J. Phys. A 34, 1109 (2001) [quant-ph/0101024].

[14] W. H. Louisell, Quantum Statistical Properties of Radiation, chap. 5, J. Wiley - 1973.

[15] G. S. Agarwal and R. R. Puri, Phys. Rev. A 39, 2969 (1989).

[16] A. B. Balantekin and N. Takigawa, Rev. Mod. Phys. 70, 77 (1998) [nucl-th/9708036].

[17] P. Hänggi, P. Talkner, and M. Borkovec, Rev. Mod. Phys. 62, 251 (1990).

[18] M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions, Dover - 1972.

[19] N. B. Conkwright, Introduction to the Theory of Equations, chap. 5, Ginn and Company - 1941.

Received on 27 May, 2003

Appendix I

The roots of the cubic algebraic equation

can be obtained by[18]

where E₊ and E_-, that must be complex conjugate, are given by

with

Appendix II

The roots of the quartic algebraic equation

can be obtained by[19]

where

and

Publication Dates

• Publication in this collection
  25 Nov 2005
• Date of issue
  Dec 2003

History

• Received
  27 May 2003
• Accepted
  27 May 2003