Ambiguities and symmetry relations in the perturbative solution of Quantum Electrodynamics

Ambiguities and symmetry relations in the perturbative solution of Quantum Electrodynamics

S. R. Gobira*, O. A. Battistel**, and M. C. Nemes*

*Universidade Federal de Minas Gerais, CP 702,

30161-970, Belo Horizonte, M.G., Brasil

**Universidade Federal de Santa Maria, CP 5093, 97119-900, Santa Maria, RS, Brasil

Received 20 March, 2000

We show that ambiguities and symmetry violations arising in one loop calculations can always be avoided provided the regularization scheme employed satisfies three consistency conditions. Our calculations are effected by assuming only implicitly the presence of a regulator in the integrand. We demonstrate in this way that there is a set of three relations involving divergent integrals of the same degree of divergence which are the source of both ambiguities and symmetry violations in Quantum Electrodynamics. Moreover we give analytical expressions for the finite parts of amplitudes off the mass shell systematized in terms of a set of special functions. Ward identities require hightly nom trivial relations involving those functions which we also derive.

I Introduction

Nowadays, the most consistent quantum field theory in the description of physical observables is Quantum Electrodynamics (QED). An essential step for the success of that theory was, undoubtedly, finding a consistent interpretation of the infinites that appear in the calculation of perturbative amplitudes. The procedure that allows for the elimination of those infinites in favor of a new definition of parameters is known as Renormalization Theory . Topics Renormalisation and Symmetries are deeply related. The symmetry relationships in QED have origin directly in the lagrangean and automatically associate several physical processes.The original content of symmetries should be reflected in the calculated amplitudes with Feynman rules in each order of the perturbative expansion. The symmetry relationships among Green's functions of a theory are Ward identities. In theories with non trivial symmetries the renormalizability critically depends on the cancellation of divergences among different sections of the theory as dictated by Ward identities. Traditionally the treatment of divergences in Quantum Field Theory is made through the adoption of a regularization scheme so that they can be manipulated and calculated. In the literature countless techniques of regularization exist. The application of those techniques in renormalizable theories had a relative success, since they can be used as intermediate and are totally removable steps from the final results. The method that has proven more consistent in all situations in which it applies is Dimensional Regularization [4][6]. It has however problems when the g⁵ Dirac matrix is involved. That technique is difficult to be implemented in the case of unrenormalizable theories , once the regularization parameter, that cannot be removed, is the space-time dimension and therefore of difficult physical interpretation. On the other hand, other techniques, as the Pauli-Villars regularization [6] that proposes a parameter of reasonable interpretation as a cut parameter in the momentum, has other undesirable problems: unitarity violation and ambiguities associated to the choice of the internal momenta of the "loops". A fundamental point that all the current techniques of regularization have in common is the modifications on the integrand of the mathematical expressions dictated by the Feynman rules for the several processes. Recently a method has been proposed where regularization is only implicit [1]. One never needs to evaluate divergent objects. The proposed technique separates the divergent from the physical (external momentum dependent) parts of the amplitude. Consistency is achieved by means of three relations between divergent integrals of same degree of divergence as will be shown here in the context of QED. In the present work we use arbitrary momentum label in the essential one loops amplitudes of QED and investigate the conditions under which the results are unambiguous and symmetry preserving. That set of consistency conditions is automatically satisfied for the Dimensional Regularization. Then we can say that any regularization which satisfies those three consistency conditions automatically will be a consistent prescription. Concluding we show that a regularization scheme exists in four dimensions that possesses all the virtues of Dimensional Regularization where it is applied, without, however, presenting its restrictions with respect to the g⁵ matrix. In [5] it is shown that there exists at least two possible regularizations.

The present work is organized as follows: in section II we briefly give an account of the method we will use. All the explicit Ward identity calculations in the section III are performed using the implicit regularization scheme and some functions that we define in the ^Appendix. In section IV we will verify then that the set of consistency conditions are satisfied for the Dimensional Regularization and the one parameter Pauli-Villars Regularization will always violate them.

II The Method: Implicit Regularization Scheme

The implicit regularization scheme can be presented in the form of its essential calculational steps:

- After taking the trace of Dirac matrices, we identify all of the divergent integrals.

- Manipulate each one of those integrals, just at the level of the integrand, until dependence on the external momenta is strictly contained in finite integrals. This can be accomplished by a Taylor expansion arond the external momentum p_i = 0 .

- The finite integrals should be integrated directly without restrictions - The unambiguous divergent parts, now independent of the external momenta, are reduced to the basic forms:

III Ward identities in QED

The application of the of Feynman rules for QED allows us to construc the corresponding amplitudes to the pertinent physical processes. That takes us to the immediate identification of the diagrams for which the power counting reveals the possibility of divergences. The content of symmetry of the theory establishes relationships among the diagrams, that should be satisfied for any method used in the manipulations and calculations.

We will use an arbitrary label for the internal momenta of the loops and calculate the amplitudes showing that, in the present case, ambiguities as symmetry violations are related to the same set of divergent integrals.

A. The tad-pole diagram

The Feynman rules give

Where we use the notations: a.b º a_nbⁿ, /a º g_naⁿ and ò_L means implicit regularization.

In agreement with the method explained in section II the first step gives

where

and

The first integral has cubic divergence and the second quadratic divergence.We will use the quadratically divergent integral to show how the method works.

In the second step we used the identity equivalent to a Taylor expansion arond aq to qet

eliminating the terms that don't contribute to the integral we have :

the last term between parenthesis is finite. The finite integrals cancel mutually as be verified explicitly. We can write then:

In a similar way we will have

The amplitude can be written as:

Notice the presence of the ambiguity related by the label of the internal momentum (dependence on a).The fermionic amplitude of a point should vanish identically because it possesses an odd number of vectorial indexes (coupled with an odd number of external photons). That is dictated by the Furry theorem [9]. On the other hand, the conservation of the vectorial current (gauge invariance) demands that the contraction with the momentum of the external photon is also zero giving rise to the following Ward identity:

The conditions

are necessary and sufficient for obtaining an unambiguous result. Notice that, by Dimensional Regularization, the amplitude vanishes too. In the 2w-dimensional space we can make a shift in (4) and therefore the amplitude vanishes. In Dimensional Regularization the consistency conditions (13), (14) and (15) are also satisfied. Therefore as becames clear in this example one of the reasons behind the consistency of Dimensional Regularization is this. Now let us proceed to investigate whether the same set of conditions appear in other processes

B. The photon self-energy

The Feynman rules give

We can write it as

where

and

In the last step we made the substitution p = aq and p^¢ = (a-1)q.

Treating the amplitude in the same way as before and using the consistency conditions (14) and (15) to avoid ambiguities(dependence on a) we can write the amplitude as

The finite functions are all listed in the ^Appendix.

The amplitude should satisfy to the Ward identity as demanded by the gauge invariance.With this expression we can see that the consistency conditions (13) is also need in order to satisfy the Ward identities

C. The electron self-energy and the vertex correction

For the electron self-energy the Feynman rules give

where we use q = ap and q^¢ = (1 - a)p

We work with m as the photon mass to avoid infra-red divergence and take m = 0 in the result.Treating the amplitude again as before (using the consistency conditions (14) to avoid ambiguities) we can write the amplitude as

Here, as before all the finite contributions are listed in the ^Appendix.

In the vertex correction case we don't have ambiguities because the amplitude is logarithmically divergent and we can make a shift and eliminate a. The Feynman rules give

here

The explicit calculation of the amplitude leads to the result

The electron self-energy is related to the vertex correction by the Ward identity

When we make the contraction of the expression (28) with the photon momentum we can see that: the only way to automatically satisfy this Ward identity is if the consistency conditions (14) are satisfied. The finite part of the expression also satisfies the Ward identity. this can be shown explicitly and far from being obvious. As shown in the ^Appendix we need hightly nontrivial relations ammong the functions x_s and functions Z_s . These relations among the finite parts of the amplitudes are very important in other models too. We therefore list them all in the ^Appendix.

IV Conclusion

By Dimensional Regularization the consistency conditions (13), (14) and (15) are satisfied. Those three conditions are just necessary to obtain results unambiguous and symmetry preserving results in the calculation of divergent amplitudes in QED. We can say that the success of Dimensional Regularization in QED is due to fact that it satisfies those consistency conditions automatically. We have

and

we have

and

The last consistency condition can be written as

where g_mnrs = g_mng_rs + g_rmg_ns + g_rng_ms . Then we have

The one parameter Pauli-Villars Regularization will violate them:

first we have

and

By the second condition we have

and

Finally we have

The regularization methods can introduce terms in the calculated amplitudes which are devoid of physical meaning. Those terms many times are absorbed by a renormalization process but many times can yield results which are allien to the original theory. We conclude by stating that in the context of QED we found which are the conditions to be satisfied by ANY regularization prescription to yield unambiguous and symmetry preserving results. The same three conditions appear in other contexts such as the linear sigma model [10]. The advantage of the present prescription is that no explicit use of a regulator also is necessary. Also it applies as well to theories involving g⁵ Dirac matrix which are important in low energy hadron physics.

APPENDIX A: Used Functions

We express the results of the amplitudes in terms of functions that we will define as:

where

Functions x_s and Z_s are related by expressions as

and it has the following property

Acknowledgments

The work of M.C. Nemes was partially supported by CNPq and the work of S.R. Gobira was partially supported by CNPq and FAPEMIG.

[10] Work in progress

• [1] O.A. Battistel, UFMG - PhD Thesis (1999).
• [2] O. Battistel, M.C. Nemes, Symmetry Relations in The N.J.L. Model. Phys. Rev.D 59, 055010 (1999).
• [3] O. Battistel, A.L. Mota, M.C. Nemes, Mod. Phys. Lett. A 13, 1597 (1998).
• [4] J.D. Bjorken, S.D. Dreel, Relativistic Quantum Mechanics, McGraw-Hill, New York (1964).
• [5] E. Butkov, Física Matemática, Ed. Guanabara, Rio de Janeiro (1988).
• [6] T. Cheng, L. Li, Gauge Theory of Elementary Particle Physics, Claredon Press, Oxford (1992).
• [7] R.P. Feynman, Quantum Electrodynamics, Addison-Wesley Publishing Company, New York (1961).
• [8] R.P. Feynman, Space-time Approach to Quantum Eletrodynamics. Phys. Rev. 76, 769 (1949).
• [9] W. H. Furry, A Symmetry Theorem in the Positron Theory. Phys. Rev. 51, 125 (1937).

Appendix

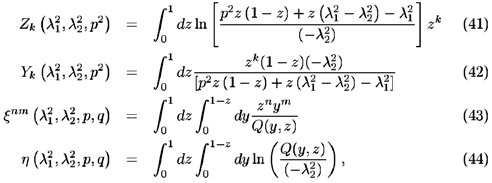
Publication Dates

• Publication in this collection
  11 Jan 2002
• Date of issue
  2000

History

• Received
  20 Mar 2000