A unifying approach to relaxation properties of chemical and colloidal gels

A unifying approach to relaxation properties of chemical and colloidal gels

Lucilla de Arcangelis^I,III; Emanuela Del Gado^II,III; Annalisa Fierro^II,III; Antonio Coniglio^II,III

^IDepartment of Information Engineering, Second University of Naples, Italy

^IIPhysics Department, University of Naples "Federico II", Italy

^IIINFM Udr of Naples and Gruppo coordinato SUN, Italy

ABSTRACT

We study the viscoelastic properties and the relaxation process in a gelling system by means of a minimal statistical mechanics model. The model is based on percolation and bond-fluctuation dynamics. By opportunely varying some model parameter we are able to describe a crossover from the chemical gelation behaviour to dynamics more typical of colloidal systems. The results suggest a novel connection linking classical gelation, as originally described by Flory, to more recent results on colloidal systems.

I Introduction

The gelation transition transforms a solution of polymeric molecules, the sol, which is essentially a viscous fluid, into an elastic solid. This happens when the bond formation between different molecules is induced and it is phenomenologically characterized by the divergence of the viscosity coefficient in the sol and by the appearence of an elastic response in the gel phase. This corresponds to the constitution inside the sol of a macroscopic polymeric structure [1], which characterizes the gel phase. This polymerization process leading to the formation of an interconnected stress-bearing network in the system is then responsible on one hand for the divergence of the viscosity coefficient h and on the other hand for the growing of a non-zero elastic modulus Y. The critical growth of the connectivity can be straightforwardly interpreted by means of a percolation transition, which starting from the work of Flory and Stockmayer [1,2,3] is practically considered as the basic model for gelation transition. Depending on the particular system the gelation can be observed by lowering the temperature, or as function of time or else of the monomer concentration in the sol. In any case close to the gelation transition the viscosity coefficient grows with a power law behaviour characterized by a critical exponent k. The onset of the elastic response in the system corresponds to a power law increasing of the elastic modulus described by a critical exponent f.

Approaching the gelation threshold complex polymeric structures are formed, characterized by different relaxation processes over many different lenght scales. Infact the relaxation functions in most of the experiments display a long time stretched exponential decay in the critical solution approaching the gelation threshold [4,5,6,7]. The relaxation process becomes critically slow at the gel point, where the onset of a power law decay is typically observed.

This complex relaxation somehow resembles what is typically observed in a supercooled liquid approaching the glass transition [8] and in general this form is interpreted in terms of many decay processes, occurring over different time scales. One has to recognize that here the relaxation process is actually controlled by the growth of the connectivity. At the gelation threshold

₀® ¥ and the relaxation functions decay as a power law [4,5]. In the gel phase the relaxation behaviour displays a variety of complex behaviours depending on the system.

These features are actually common to all gelling systems and to some extent unify their phenomenology. As long as this dynamic behaviour is controlled by the onset of a percolation transition in the system one could expect that the critical exponents k and f are univocally determined in some way in terms of the percolation transition critical exponents and are the same for all the gelling systems. On the whole the experimental data collected in many accurate experiments performed on a wide variety of systems in the latest decades do not support this picture [9]-[20]. In fact different exponents are actually measured in different systems. In general the experimental data have been considered as just scattered probably because of the experimental problems of reproducibility, showing apparently lack of universality in the gelation phenomena.

With a more accurate analysis we have noticed that the different data are not uniformly spread, but result to be close to certain values. Essentially the data come close to the critical exponents k ~ 0.7 and f ~ 2. ([9]-[12]) or else k ~ 1.3 and f ~ 3. ([13]-[20]) are observed in the experiments. On the theoretical side k ~ 0.7 and f ~ 2. correspond to the predictions due to the analogy between the gelation transition and the electric percolation network problems in d = 3 [21,22,23]. On the other hand a critical exponent k ~ 1.3 is obtained within a Rouse model approach using the scaling predictions of percolation model [22], whereas by evaluating the entropic contribution of the percolating cluster to the gel elasticity in 3d a value f ~ 3. is found [24]. Within this intriguing picture new questions are opened: our analysis suggests the possibility of two universality classes or else of one universality class, the other corresponding to an apparent critical behaviour characterizing a crossover to the real one.

Gelation phenomena are also observed in colloidal systems, that are suspensions of mesoscopic particles interacting via short range attraction: due to aggregation phenomena at low density (colloidal gelation) these systems display gel states with a power law behaviour of the viscosity coefficient and of the elastic modulus [25], as in chemical gelation. Yet the aggregation process gives rise to cluster-cluster aggregation producing a spanning cluster with a fractal dimensionality smaller than the random percolation case [26,27]. On the other hand with a weaker attraction at higher density a gelation characterized by a glass-like kinetic arrest [28] may be observed. The relaxation patterns closely recall the ones observed in glassy systems and are well fitted by the mode-coupling theory [29] predictions for supercooled liquids approaching the glass transition [28]. On the theoretical side the application of the mode-coupling theory to systems with short range attractive interaction [30,31] (attractive glasses) has been recently considered and the connection with the colloidal glass transition has been proposed.

Our approach to the problem is to develope a minimal statistical mechanics model to be able to directly link the dynamical behaviours to the fundamental elements of the model and to provide a unifying description for gelling phenomena.

The model is based on percolation clusters and on a suited dynamics [32]. Infact the percolation model has been successfully used for the description of the gelation transition [2,3] in terms of the geometrical properties but as for itself it does not give account for the dynamics. We have used the bond-fluctuation dynamics [33], which effectively takes into account the possibility of conformational changes in polymer molecules. Infact this typical feature of polymer systems does play an important role in their viscoelastic properties: the fact that the polymer molecules may change their configuration corresponds to a relevant entropic term in any free energy change and does affect the dynamics of such systems. We have studied a solution of monomers interacting via a repulsive excluded volume interaction and an attractive bonding interaction creating clusters. The question that we want to investigate is whether and to what extent colloidal gelation, colloidal glass transition and chemical gelation are related and if a unifying description is possible.

In section I we briefly describe the model and in section II and III we present the results obtained for the relaxation patterns in the case of permanent and non-permanent bond; section IV contains concluding remarks.

II The percolation dynamic model

Our model introduces within the random percolation the bond-fluctuation (BF) dynamics, which is able to take into account the polymer conformational changes [33] and it has been successfully used to study the static and dynamic properties of polymer solutions at high concentrations. We study a solution of tetrafunctional monomers at concentration f and with a probability p_b of bonds formation. In terms of these two parameters one has different cluster size distributions and eventually a percolation transition. Monomers free or linked in clusters interact via excluded volume interactions and diffuse via random local movements. According to the BF dynamics, bond vectors may vary due to the monomers displacements, with the constraints imposed by the excluded volume interaction amongst monomers and self-avoiding walk (SAW) condition for the bonds. Here the constraints produce a maximum allowed value for the bond length,but still correspond to a high variety of allowed configurations for the polymer clusters [33]. On a cubic lattice it can be shown that the bond lengths which guarantee the SAW condition are in lattice spacing units. It is very important to notice that there is no internal energy difference associated to the different bond vectors: the changes in the polymer molecules configurations correspond to negligible energy variation, which is a typical feature of polymeric systems [34,35]. In the first version of the model once the bonds are formed between two monomers, hey are permanent in time and can only vary their length.

With this model we are able to directly study the dynamic properties of the system in the sol phase as the percolation threshold is approached and in the gel phase. The gel phase and the corresponding dynamic transition correspond to the constitution of a percolating network. Below the percolation threshold the system is a sol of percolation clusters and by means of the bond-fluctuation dynamics we study their transport properties and the average relaxation time behaviour in the critical region as the incipient percolating cluster is forming. The dynamic evolution of the system above the percolation threshold gives us information on the gel phase dynamics: any elastic response in the system has then a purely entropic nature. We have performed numerical simulations of the model on the cubic lattice of different lattice sizes with periodic boundary conditions. The sites which are the vertices of a lattice elementary cell are simultaneously occupied by a monomer, with the constraint that two nearest neighbour (nn) monomers are always separated by an empty elementary cell, i.e. two occupied cells cannot have common sites. The lattice of cells, with double lattice spacing, has been occupied with probability f, which coincides with the monomer concentration on the main lattice in the thermodynamic limit [32].

Monomers are randomly distributed on the main lattice via a diffusion process, and between two nn or next nearest neighbour (nnn) monomers bonds are instantaneously created with probability p_b along lattice directions. Since most of the experimental data on the gelation transition refer to polymers with monomer functionality f = 4 we have considered this case allowing the formation of at most four bonds per monomer. We have considered lattices of size L ranging between 16 and 32 and all the data have been averaged over a sample of ~ 30 systems with different initial site and bond configurations.

First, a qualitative phase diagram has been determined, studying the onset of the gel phase varying f and p_b [32]. Then we have fixed p_b = 1 and let f vary in the interesting range from the sol to the gel phase, determining f_c ~ 0.718 ±0.005 in d = 3 [32] and the critical exponents n for the connectedness length x and g for the mean cluster size c in agreement with the random percolation model [36].

In colloids the aggregation is due to a short range attraction and in general the monomers are not permanently bonded. To take into account this feature we introduce a novel ingredient in the model by considering a finite bond lifetime

_b and study the effect on the dynamics. The features of this model with finite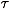 _b can be realized in a microscopic model: a solution of monomers interacting via an attraction of strength -E and excluded volume repulsion. Due to monomers diffusion the aggregation process eventually takes place. The finite bond lifetime 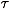_b corresponds to an attractive interaction of strength -E that does not produce permanent bonding between monomers, and 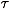_b ~ e^E/KT. Due to the finite 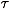_b, in the simulations during the monomer diffusion the bonds between monomers are broken with a frequency 1/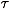_b. Between monomers separated by a distance less than l₀ a bond is formed with a frequency f_b. For each value of 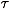_b we fix f_b so that the fraction of present bonds is always the same [37]. We study the relaxation properties of the system in the sol and in the gel phase for the case of permanent bonds and bonds with a finite lifetime.

III Relaxation properties: permanent bond case

To investigate the nature of the dynamic transition at the chemical gelation here we study the equilibrium density fluctuation autocorrelation functions f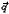(t) given by:

where is the position of the i-th monomer at time t, N is the number of monomersand the average á... ñ is performed over the time t¢. We also study the mean square displacement of the particles .

In Fig. 1 we present these time autocorrelation functions as function of the time calculated on a cubic lattice of size L = 16. The data have been averaged over ~ 10 up to 10⁵ time intervals and over 20 different initial configurations of the sample. As the monomer concentration f approaches the percolation threshold f_c, f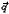(t) displays a long time decay well fitted by a stretched exponential law with a b ~ 0.30 ±0.05. At the percolation threshold the onset of a power law decay is observed as it is shown by the double logarithmic plot of Fig. 1 with an exponent c [28]. As the monomer concentration is increased above the percolation threshold in the gel phase, the long time power law decay of the relaxation functions can be fitted with a decreasing exponent c, varying from c ~ 1. at f_c to c ~ 0.2 well above f_c. This behaviour well agrees with the one observed in gelling systems investigated in the experiments of refs.[28]. It is interesting to notice that this kind of decay with a stretched exponential and a power law reminds the relaxation behaviour found in spin-glasses [38]. In Fig. 2 the mean square displacement of the particles is plotted for different values of f approaching f_c as function of the time. At long times a diffusive behaviour is displayed and the diffusion coefficient decreases but remains finite also above f_c. However the diffusion coefficient of clusters of size comparable with the connectedness length goes to zero with the same exponent as the relaxation time [32].

These results very well reproduce the relaxation patterns in the experiments as reported in ref.[4,5,6]. The relaxation time diverges at the percolation threshold due to the divergence of the connectivity and this correponds to the occurrence of the power law behaviour, also observed in the gel phase in TMOS silica gels [4] and in NIPA gel [5].

IV Relaxation properties: non-permanent bond case

We study now the relaxation properties of our model in the case when the bonds have a finite lifetime

_b. At the equilibrium we have evaluated the relaxation time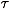 by which the relaxation function f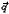(t) has become ~ 0.1. In Fig. 3 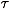is plotted as function of the monomer concentration f for different 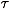_b. For comparison we have also shown the behaviour of 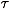in the case of permanent bonds, which displays a power law divergence at the percolation threshold f_c. We notice that for finite bond lifetime 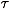_b the relaxation time increases following the permanent bonds case (chemical gelation), up to some value f^* and then deviates from it. The longer the bond lifetime the higher f^* is. In the high monomer concentration region, well above the percolation threshold, the relaxation time in the finite bond lifetime case again displays a steep increase and a power law divergence at some higher value. This truncated critical behaviour followed by a glassy-like transition has been actually detected in some colloidal systems in the viscosity behaviour [39,40].

These results can be explained by considering that only clusters whose diffusion relaxation time is smaller than

_b will behave as in the case of permanent bonds. Larger clusters will not persist and therefore will not be relevant in the dynamics: the finite bond lifetime introduces an effective cut-off on the size of relevant clusters and keeps the macroscopic viscosity finite [41]. As the concentration increases the final growth of the relaxation time is due to the crowding of the particles.

To compare the dynamics with the chemical gelation case, we have calculated f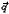(t) as defined in eq.(1). As the monomer concentration increases the system displays relaxation patterns that are typical of glassy dynamics. In Fig. 4 the relaxation funtions f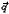(t) as function of time are plotted in the case 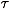_b = 1000 MCstep/particle. The different curves refer to different values of the monomer concentration (f varies from below to well above f_c). If for small concentrations the behaviour of the autocorrelation function is well fitted by a stretched exponential decay, the curves in Fig. 4 for high monomer concentrations exhibit a two step decay that is closely related to the behaviour observed in supercooled liquids characterizing the structural arrest due to the formation of blocked structures (cages). Therefore we have fitted the curves using the mode-coupling b-correlator [29], corresponding to a short time power law and a long time von Schweidler law , giving the exponents a ~ 0.33 ±0.01 and b ~ 0.65 ±0.01. At long times the different curves obtained for different f collapse into a unique master curve by opportunely rescaling the time via a factor 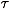(f). The master curve is well fitted by a stretched exponential decay with b ~ 0.50 ±0.06 (inset of Fig. 4). The characteristic time 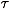(f) diverges at a value f_g ~ 0.963 ±0.005 with the exponent g ~ 2.33 ±0.06. This value well agrees with the mode-coupling prediction g = 1/2a + 1/2b [29]. Finally, in Fig. 5 is plotted for the different values of f displaying the typical plateau pattern, with the diffusion coefficient going to zero as f approaches f_g.

By comparing these results with Figs. 1 and 2 we notice that when bonds are permanent (chemical gelation) the cluster effect dominates and the jamming is negligible. In the case of finite 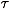_b the divergence of the relaxation time is due to the contribution of both the cluster formation and the jamming of the particles, and we find the two step relaxation which is the signature of the cage effect. When t_b is large enough (that corresponds to strong attraction) the cluster effect will dominate and the slow dynamics will exhibit features more closely related to chemical gelation (Figs. 1 and 2). The only difference is that in the limit 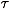_b ® ¥ we expect that the spanning cluster will have the structure of the cluster-cluster aggregation model instead of random percolation.

V Conclusions

Our model reproduces many relevant aspects of the gelation transition. In particular it has allowed to determine the viscoelastic properties critical exponents in a case of strong gelation, and shows a stretched exponential decay as the gel point is approached and a power law decay at the transition and in the gel phase. In the case of bonds with a finite lifetime, the relaxation properties show a behaviour similar to what found in glassy systems, with a two step decay in the relaxation functions. In conclusion, these results suggest a unifying approach for chemical gelation, colloidal gelation and colloidal glass transition. In chemical gelation and colloidal gelation the cluster formation is the main responsible for the slow dynamics that is expected to be of the same type of Figs. 1 and 2. In colloidal systems for weak attraction and high concentration the system crosses over from colloidal gelation to colloidal glass due to the combined effects of clusters and particle jamming.

All the simulations have been performed on the IBM Linux Cluster at CINECA. This work has been partially supported by MURST-PRIN-2000 and 2002, MIUR-FIRB-2002 and by the INFM Parallel Computing Initiative.

References

[1] P. J. Flory The Physics of Polymer Chemistry Cornell University Press (Ithaca) 1954.

[2] P. G. De Gennes Scaling concepts in polymer physics Cornell University Press (Ithaca) 1980.

[3] M. Adam, A. Coniglio, and D. Stauffer, Adv. in Polymer Sci. 44, 103 (1982).

[4] J. E. Martin, J. P. Wilcoxon, and J. Odinek, Phys. Rev.A 43, 858 (1991).

[5] F. Ikkai, M. Shibayama, Phys. Rev. Lett. 82, 4946 (1999).

[6] S. Z. Ren, C. M. Sorensen, Phys. Rev. Lett. 70, 1727 (1993).

[7] M. Adam, M. Delsanti, J. P. Munch, and D. Durand, Phys. Rev. Lett. 61 706 (1988).

[8] P. Johari, J. Chem. Phys. 58, 1766 (1973).

[9] M. Djabourov, J. Leblond, and P. Papon, J. Phys.(France) 49, 333 858 (1988); M. Djabourov, Contemp. Phys. 29, 273 (1988); G. C. Fadda, D. Lairez, and J. Pelta, Phys. Rev. E 63, 061405 (2001).

[10] F. Devreux, J. P. Boilot, F. Chaput, and L. Malier Phys. Rev. E 47, 2689 (1993).

[11] M. A. Axelos, M. Kolb, Phys. Rev. Lett. 64, 1457 (1990).

[12] M. Tokita, K. Hikichi, Phys. Rev. A 35, 4329 (1987).

[13] M. Adam, D. Lairez, M. Karpasas, and M. Gottlieb, Macromolecules 30, 5920 (1997).

[14] C. P. Lusignan, T. H. Mourey, J. C. Wilson, and R. H. Colby, Phys. Rev. E 52, 6271 (1995); C. P. Lusignan, T. H. Mourey, J. C. Wilson, and R. H. Colby, Phys. Rev. E 60, 5657 (1999); R. H. Colby, J. R. Gillmor, M. Rubinstein, Phys. Rev. E 48, 3712 (1993).

[15] D. Lairez, M. Adam, J. R. Emery, and D. Durand, Prog. Coll. Polym. Sci. 90, 37 (1992).

[16] T. Nicolai, H. Randrianantoandro, F. Prochazka, and D. Durand Macromolecules 30, 5897 (1997).

[17] M. Takahashi, K. Yokoyama, T. Masuda, and T. Takigawa, J. Chem. Phys. 101, 798 (1994).

[18] J. E. Martin, D. Adolf, and J. P. Wilcoxon, Phys. Rev. Lett 61, 2620 (1988).

[19] R. H. Colby, B. K. Coltrain, J. M. Salva, and S. M. Melpolder in Fractal Aspects of Materials: Disordered Systems, edited by A. J. Hurd, D. A. Weitz, and B. B. Mandelbrot (Materials Research Society, Pittsburgh, PA, 1987).

[20] M. Adam, M. Delsanti, and D. Durand, Macromolecules 18, 2285 (1985); M. Adam, M. Delsanti, D. Durand, G. Hild, and J. Munch Pure Appl. Chem. 53, 1489 (1981).

[21] P. G. de Gennes, J. Phys. Lettres 37, L-1 (1976).

[22] P. G. de Gennes, C. R. Acad. Sc. Paris B 131, (1978).

[23] K. Broderix, H. Loewe, P. Mueller, and A. Zippelius Europhys. Lett. 48, 421 (1999).

[24] M. Daoud, A. Coniglio, J. Phys. A 14, 30 (1981).

[25] V. Trappe, V. Prasad, L. Cipelletti, P.N. Segre and D. A. Weitz, Nature 411, 772 (2001); V. Trappe and D. A. Weitz, Phys. Rev. Lett. 85, 449 (2000).

[26] P. Meakin, Phys. Rev. Lett 51, 1119 (1983).

[27] A. D. Dinsmore and D. A. Weitz, J. Phys.: Condens. Matter 14, 7581 (2002).

[28] H. Gang, A. H. Krall, H. Z. Cummins, and D. A. Weitz, Phys. Rev. E 59, 715 (1999); F. Mallamace, P. Gambadauro, N. Micali, P. Tartaglia, C. Liao, and S.H. Chen, Phys. Rev. Lett. 84, 5431 (2000).

[29] W. Göetze in Liquid, Freezing and Glass Transition, eds. J. P. Hansen, D. Levesque and P. Zinn-Justin, Elsevier (1991).

[30] J. Bergenholtz, M. Fuchs, and Th. Voigtmann, J. Phys.: Condens. Matter 12, 4341 (2000).

[31] K. Dawson, G. Foffi, M. Fuchs, W. Göetze, F. Sciortino, M. Sperl, P. Tartaglia, Th. Voigtmann, and E. Zaccarelli, Phys. Rev. E 63, 011401 (2001); E. Zaccarelli, G. Foffi, K. A. Dawson, F. Sciortino, and P. Tartaglia, Phys. Rev. E 63, 031501 (2001).

[32] E. Del Gado, L. de Arcangelis, and A. Coniglio, J. Phys. A 31, 1901 (1998); E. Del Gado, L. de Arcangelis, and A. Coniglio, Europhys. Lett. 46, 288 (1999); E. Del Gado, L. de Arcangelis, and A. Coniglio, Eur.Phys. J. B 2, 352 (2000); E. Del Gado, L. de Arcangelis, and A. Coniglio, Physical Review E 65, 41803 (2002).

[33] I. Carmesin and K. Kremer, Macromolecules 21, 2819 (1988).

[34] M. Doi, S. F. Edwards The Theory of polymer Dynamics Clarendon Press, Oxford (1986).

[35] J. Ferry Viscoelastic properties of polymers Wiley New York 1980.

[36] A. Aharony, D. Stauffer, Introduction to percolation theory Taylor and Francis, London (1994) Cornell Univ.Press, Ithaca 1953 .

[37] E. Del Gado, A. Fierro, L. de Arcangelis, and A.Coniglio to appear on Europhys Lett. and in preparation.

[38] A. T. Ogielski, Phys. Rev. B 32, 7384 (1985).

[39] F. Mallamace, S.H. Chen, Y. Liu, L. Lobry, and N. Micali Physica A 266 (1999); F. Mallamace, R. Beneduci, P. Gambadauro, D. Lombardo, and S.H. Chen, Physica A 302, 202 (2001).

[40] F. Laflèche, D. Durand, and T. Nicolai preprint (2002).

[41] A. Coniglio J. Phys.: Condensed Matter 13, 9039 (2001).

Received on 23 April, 2003

Publication Dates

• Publication in this collection
  11 Nov 2003
• Date of issue
  Sept 2003

History

• Accepted
  23 Apr 2003
• Received
  23 Apr 2003