Revisiting the first-principles approach to the granular gas steady state

Revisiting the first-principles approach to the granular gas steady state

R. C. Proleon; W. A. M. Morgado

Departamento de Física, Pontifícia Universidade Católica do Rio de Janeiro, CP 38071, 22452-970 Rio de Janeiro, Brazil

ABSTRACT

We extend a Fokker-Planck formalism, previously used to describe the behavior of a cooling granular gas, with a Hertzian contact potential and viscoelastic radial friction, giving a velocity dependent coefficient of restitution. In the present work, we study the more general case of a steady-state with finite kinetic energy, far from equilibrium, due to the coupling to an external energy-feeding mechanism. Also from first-principles, we extend the validity of the former results.

1 Introduction

The problem of a granular gas (GG) at a steady-state, under the action of an energy feeding mechanism, has been extensively studied by means of theoretical [1, 2, 3] and experimental methods [4, 5]. A GG presents many interesting and non-trivial properties concerning its statistical behavior, such as non-Gaussian velocity distributions [4, 6], energy equipartition breakdown [6, 7], vortices and clustering [8, 9, 10]. These interesting properties are a direct consequence of the inelastic behavior of a GG. No matter how small, any amount of inelasticity will make a GG completely different, in long times, from an elastic molecular gas. For instance, no matter how small the inelasticity is, the GG will eventually lose all its internal kinetic energy [11]. However, a more fundamental approach unifying all these aspects of granular physics is still laking [13].

With the goal of obtaining a basic first-principles approach to the problem of an inelastic GG, Schofield and Oppenheim [12] derived a set of Fokker-Planck equations for the distribution of positions and velocities for the grain's centers of mass of a GG at the (not necessarily homogeneous) cooling state (no energy-feeding mechanism) tending to true thermal equilibrium. This is a very general method that depends on a time-scale separation between the internal relaxation processes of a grain (fast variables) and the evolution of the long wavelength phenomena for the GG (slow variables) [14]. It gives the velocity dependence for the coefficient of restitution found elsewhere [15, 16, 17].

In the present work, we introduced a well known energy-feeding mechanism to extend the validity of that previous approach to a GG in a steady-state of finite granular kinetic energy. The basic steps leading to an equation describing the time-evolution for the distribution include postulating the inelastic Boltzmann-Enskog equation [8, 9], adding energy feeding mechanisms such as the ''democratic" vibration model [1], and deriving Fokker-Planck equations based on a first-principles expansion around equilibrium [12], kinetic theory methods [18], Monte Carlo methods or molecular dynamics simulations [19]. Most of these are effective approaches that ignore the detailed collisional dynamics. Some authors did indeed take the time dependence for the collisional dynamics into account in their models [20]. Naturally, most models in the literature are based on a posteriori justifications for their assumptions.

We believe our model can show its usefulness in helping to set some of the stochastic and kinetic theory models used to describe granular gases in better theoretical footing. It explores the same expansion methods [14] used to derive stochastic equations for granular gases in the rapid flow state. In special, careful steps are taken to ensure that an appropriate non-equilibrium steady-state is correctly taken into account as the basis for the expansions methods. The Fokker-Planck equation thus obtained can be used as the starting point for the development of kinetic theory methods appropriate for granular gases. For didactic reasons, we keep most of the calculation details in the main body of the text.

In order to maintain our model system in a constant energy steady-state, we make use of the democratic model of energy feeding and derive the inelastic Boltzmann equation in that context. This mechanism is used because of its practicallity. More realistic energy-feeding mechanisms can be modeled [6, 7]. It should be noticed that the typical granular energies for the GG steady state, compared to that of the thermal equilibrium situation, may typically be of the order of 10¹² or larger.

This paper is organized as follows. In Section II, we describe the microscopic model. In Section III, we describe the energy-feeding mechanism used in the paper. In Section IV, we eliminate the fast degrees of freedom for the system and obtain the appropriate Fokker-Planck equations and the viscoelastic friction coefficient. In Sections V, VI, VII and VIII, we obtain the BBGKY hierarchy and proceed to make the multiple time-scale analysis and to obtain the appropriate Boltzmann equation for the GG. In Section IX, a Sonine polynomials expansion is obtained for the distribution and its moments analyzed. In Section X, we analyze the properties of the steady-state distribution. In Section XI, we summarize the results and make our concluding remarks.

2 Fokker-Plank approach

We will follow closely the method used by Schofield and Oppenheim [12] and study a system of N spherical, smooth and identical grains of mass m constituted by M atoms, M >> 1. The grains are large enough making quantum effects irrelevant. The only frictional forces acting on the particles are radial, along the collisional axis for two particles. The positions and momenta of the grains are defined below:

r^Nº {r₁,r₂, ¼,r_N} and p^Nº {p₁,p₂,¼,p_N}.

The microscopic degrees of freedom are atomic coordinates x^MN and atomic momenta p^MN associated to each atom of every grain. We can simplify the notation by grouping these two sets of coordinates into:

c_Iº {x^MN, p^MN}, and c_Tº {r^N, p^N}.

Thus, the complete Hamiltonian can be partitioned as

where the terms above are given in the sequence.

The granular Hamiltonian:

The internal Hamiltonian:

The interaction (coupling) term:

The probability density for the system evolves according to the Liouvillian operator defined by:

L = L_I + L_T + L_f

where

and

The Liouville equation reads

In the expression above, we need to average out the terms containing internal degrees of freedom in order to obtain an effective equation for the remaining granular degrees of freedom.

3 Energy feeding - Democratic Model

For dissipative systems, the rate of kinetic energy (E) loss due to the inelasticity during the collisions is given by

In order to keep the system in a non-trivial steady-state, it is necessary to feed kinetic energy into it. In the sequence, we describe the so-called democratic model [1], which is equivalent to coupling the GG with a granular heat-bath.

We assume that each grain in the system will periodically gain random momentum. That momentum is assumed to be a vectorial random variable, with fixed amplitude (in fact it is a set of N random variables)

where the unit vector is uniformly distributed on the sphere. It obeys:

< > = 0 and < ² >= z².

The effect on the distribution r(r^N, p^N, c_I,t) corresponds to a shift that can be written as

We assume that all grains are hit periodically, and simultaneously, with a period t₀. The heating rate corresponds to

It is necessary to take the limits z, t₀® 0, keeping the ratio º M_z fixed. We obtain exactly:

Hence, the time evolution term for the distribution, corresponding to the interaction with the heat bath, will be:

The full Liouville-like Master Equation for the GG (now an open system) becomes

Steady-state distribution:

In order to study the GG's steady-state, we need to make suitable expansions around a reference state. Our goal is to use a reference state that approximates the true steady-state solution r_SS(c_I,c_T). That state can be chosen by noticing that a typical steady-state has its internal and granular degrees of freedom almost uncorrelated. A suitable state for expansions is given by

where f(c_T) º ò dc_I r_SS(c_I, c_T), and

The form of Eq. 9 is not the same as the steady-state solution r_SS but it will stand for the expansion reference state used for obtaining a stochastic equation for the distribution of the granular degrees of freedom.

4 Elimination of fast degrees of freedom

The exact Liouville-like equation, Eq. 8, is unmanageable and can only be made tractable by eliminating the microscopic (fast) degrees of freedom through an averaging process [21]. Thus, our goal is to find an effective equation for the reduced granular distribution:

We use the method of eliminating the fast variables [14, 21]. The idea is to consider some naturally occurring small parameter that sets the time-scale differences. In previous models for granular systems, that role was played by the mass ratio e = [12] reflecting the large number of atoms constituting a grain. However, for a realistic granular steady-state, the parameter e has to be modified in order to take into account that the granular temperature

obeys T_g >> k_BT. Since

the parameter sets the time scale separation for the granular gas. A typical value for it is of the order 10^–3 whereas for previous models [12] it was of the order of 10^–9. The Liouville equation can be rewritten in a way that makes explicit the role of e, associated with the slow part of L [12]

where

and

In order to average over the fast degrees of freedom, we define a projection operator 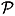, projecting r onto the fast variables, and its complement 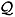= 1 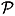– . The projection operator must satisfy [14] (see appendix)

A solution is given by the projection operator 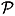acting upon a dynamical variable g º g (c_T, c_I,t) as

where is a function of the form of Eq. 9:

where we see that ò dc_I (r, c_I) = 1.

The following identities guarantee that the condition given by Eq. 13 is satisfied:

and

We multiply Eq. 12 on the left by 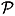and also by 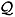in order to obtain

By using the fact that the projectors obey

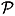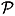
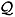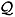
²º , = = 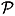0, and 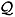²º ,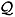

we can write

where

By switching to the slow time scale s = et we obtain

We use an expansion for z as a function of the parameter e

and substitute it for z in Eq. 20. By grouping terms of equal order in e we have

From above, we obtain the solution for z⁽⁰⁾ and z⁽¹⁾:

By substituting the expression for z⁽¹⁾ in Eq. 19, we obtain an equation for y

Now, it is necessary to compute the right hand side of the equation above. The first term is given by:

where á 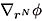ñ _o = ò dc_I

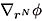. In order to find the second term, we need to calculate

where the first term of the right hand side cancels identically. By writing L_T explicitly in the second term we obtain

It is easy to show that [12]

where

Hence

and

In order to operate B onto Cy, we write B in a suitable way

Using that

òd c_I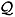º 0,

we obtain

Therefore

where the inverse operator of E can be written as [12, 21]

By substituting this into Eq. 30, we have

Since , we obtain

where

Adding up the results above, and switching back to the time-scale t = es, we obtain a Fokker-Planck equation for the reduced granular distribution

The equation above can be expressed in a more convenient form as [12]

where, for short-ranged potentials, the radial friction coefficient is given by [1,15,22]

Eq. 35 has the same form as the one obtained by Schofield and Oppenheim [12], except for a new energy-injecting term. This fact shows their coherence and a posteriori justifies their use in deriving the behavior of a system of grains with T_g >> k_BT [15]. We have now established the correct form for the basic equation of our model and can proceed to study some of their physical properties. The Fokker-Planck equation 35 is the starting point for the hydrodynamic analysis. Its validity is based on the separation of internal and granular time-scales given by the condition that the parameter e has to be small. However, in order to derive, from Eq. 35, the hydrodynamic equations appropriated for the granular steady-state, we need a few more physical assumptions, concerning the rate of energy dissipation, the number density of the system and the rate of energy feeding.

5 BBGKY Hierarchy

In the following we simplify the notation by letting x_n stand for (r_n, p_n). We define the reduced distributions below

By integrating Eq. 35 and using the definition of Eq. 37, we can compute the equations for the one-particle density f⁽¹⁾ and pair density f⁽²⁾. For f⁽¹⁾ that reads [12]:

Similarly for f⁽²⁾ [12]:

We shall estimate the order of magnitude of each term in both Eqs. 38 and 39). We assume the distribution to be uniform, that is f⁽ⁿ⁾º f(p), we obtain [12]

where

and

with

In the next section we use the time-scale separation method in order to obtain an inelastic Boltzmann equation for the granular gas in the democratic vibration regime.

6 Time-scale separation

We shall express the distribution functions as depending implicitly on the variable t trough explicit variables [23] t₀, t₁, t₂, t₃, t₄, ..., defined by

t₀ = s, t₁ = qs, t₂ = n^*s, t₃ = q²s, t₄ = n^*qs,¼

Then, the time derivative becomes

The distributions f⁽ⁿ⁾ will be expanded perturbatively as

We substitute equations (42) and (43) into (38) and collect terms to the correct order in the small parameters obtaining

Similarly for (39)

For t₀ we impose the initial condition

By canceling the secular terms (for t ® ¥) we obtain

The following consistency equations must be satisfied

The solutions for the Eqs. 45 and 46 are respectively

7 The Boltzmann collisional term

When t₀ ® ¥, we obtain from Eqs. 48 and 50

where S₁₂ = . Using the definitions of L¹ and S₁₂, we obtain

Using the property

K²S₁₂ = I²S₁₂ para t₀® ¥,

yields

Making use of the Bogoliubov's scheme integration[23]

we finally obtain the collisional term

where s(W) = bdbd [24] and and are the momenta of grains before the collision that generate p₁ and p₂.

8 The dissipative contribution and the energy feeding term

Equation (49) gives us

The first term on the right hand side of the equation above is negligibly small when t₀® ¥. It is due to the application of operator L¹S₁₂ to the integral [23]. Hence, by using explicitly the operator N¹, the above equations becomes

We can write this last equation as a Fokker-Planck equation

At low dissipation, we can approximate [22]

where f₁₂ is the elastic potential energy between grains. We define the granular temperature T_g by

At the low density, low dissipation limit, the distribution is nearly Gaussian:

The inelastic contribution is then

where A is given by [22]

for a Hertzian potential f₁₂.

The dissipative contribution reads

We finally obtain the Inelastic Boltzmann Equation:

The form of Eq. 63 is slightly different from the one used in reference [25]. However, a similar form has been proposed recently for a driven elastic hard sphere model that reproduces the physics of an inelastic GG [26]. These distinct equations should reproduce the same physics in the limit of a low density, low dissipation GG. We will check this in the next section.

9 Homogeneous Cooling State - HCS

By turning off the energy source, the granular temperature will tend to zero [27]. For an initially homogeneous system, the non-Gaussian velocity distribution has been obtained for systems with constant coefficients of restitution [28]. However, this is an approximation that becomes invalid as instabilities develop [29]. Since our model shows a velocity dependent coefficient of restitution, we need to study whether these instabilities are indeed present at long times, or disappear as shown for systems with velocity dependent coefficients of restitution [25].

9.1 Sonine Polynomials Expansion

Eq. 63 is the starting point for the asymptotic analysis. We express it in terms of the velocity:

where M_x = 0 and » 0.

We assume that the distribution scales with the granular velocity v₀ as [1]

where

s₀ being the granular diameter and v₀º v₀(t) is given by T_g(t) = (t).

We obtain

where

and

The approximations obey

The function (c,t) will be expanded by means of Sonine polynomials

where

We define the coefficients

these will be useful in the sequence.

9.1.1 Calculation of m₂

In this case, the term corresponding to I₁(, ) cancels out due to the symmetry of the integrand [24]:

The second term does contribute to m₂:

where we used .

9.1.2 Calculation of m₄

From the definition:

We use the results in Ref. [25] to obtain

and

The coefficient m₄ then reads

9.2 Long-time behavior

The granular temperature T_g º mv_o(t)² satisfies [25]

where A = gT_g^3/5 and B = v₀(t)n.

Expressing Eq. 76 as a function of the variable u = T_g/T_go, where T_go is the initial granular temperature, we obtain

The solution is given by

where

It is the equivalent of Haff's law [27] for systems with velocity dependent coefficients of restitution. The time dependence of a₂ is given by [25]:

The equation above agrees with Eq. (53) from the first article on Ref. [25]. Rewriting Eq. 79 as a function of u gives us

where

At this order of approximation, the solution is given by

The system tends to exhibit a Gaussian velocity distribution at long-times, as it becomes more elastic [25]. The cooling state for low densities and low dissipation is thus well described by Eq. 63.

10 Steady-state

We now check the validity of our model against the results obtained from the inelastic Boltzmann-Enskog method [25] at the low density, low dissipation limit.

10.1 Collision operators

When the GG is acted upon by an energy-feeding mechanism, such as the democratic model defined earlier (M_z > 0), a steady-state distribution tends to develop at the point where the rate of energy injection equals the rate of energy dissipation. The Dissipation-Vibration operator is given by

At the steady state, the granular temperature is a constant and

giving the steady-state value

where we used A = g.

Thus, the operator I₂ can be put on the convenient form:

10.2 Distribution Tail

It is important to understand the behavior of distribution on the limit of largest velocities [1]. We shall study I(, ) = I₁(, ) + I₂(), when c >> 1, separately. In order to determine the behavior of the system at large velocities we will follow the Ansatz

For I₁, we shall use the well known form [1]

For I₂, we notice that

and

The operator I₂() thus becomes

for c >> 1.

For all values of c, we have

In the limit of large c, and using

we derive an equation that allows us to calculate j (at highest order on c):

The solution for the equation above is given by

Since

the integral in Eq. 86 diverges as

Thus,

The result above shows that the overpopulation of the velocity tails will decrease with time, as was shown previously in Ref. [25].

11 Conclusions

The main motivation for the present work is to reformulate a first-principles approach to the stochastic behavior of a granular gas [12], done previously in the context of a cooling granular system, in order to include an energy feeding mechanism, in this case, the democratic model [1]. We believe this to be important since the results obtained in Ref. [12] have been successfully applied to describe the inelastic behavior of grains during a collision [15] and to derive the hydrodynamics of dilute granular gases [22].

Technically, we eliminate the fast (internal) degrees of freedom from the most general Liouville-like Master-Equation for the complete system. That is in fact a Liouville equation plus an energy-feeding term coupling the system to a thermal bath. A naturally occurring small parameter setting the time-scales is (typically) in this case

The expansion leads to a Fokker-Planck equation that incorporates the energy feeding term, and shows to be consistent, in form, with the one obtained previously [12]. In order to study the granular hydrodynamic from it, we use the time-extension method [23] and obtain, as a consistency condition, a modified Boltzmann Equation appropriate for low density, low dissipation limit. Comparing with Ref. [25], we re-obtain the Sonine expansion results in lower order in density and dissipation, as expected. We also study the distribution's large velocity dependence for the cooling state and the constant energy steady-state and conclude that the results are consistent, on the correct approximation order, to the ones obtained by rather different methods [25].

In summary, the method satisfactorily describes the physics of inelastic, energy-fed systems at the low density, low dissipation limit. The stochastic equations obtained are consistent with the ones obtained by other methods, thus being able to serve as a basis for other theories describing flowing granular systems.

References

[1] T.P.C. Van Noije, and M.H. Ernst, Granular Matter 1, 57 (1998).

[2] T. Schwager and T. Pöschel, Phys. Rev. E 61, 1716 (2000).

[3] H.J. Herrmann, Physica A 313 (2002) 188.

[4] F. Rouyer and N. Menon, Phys. Rev. Lett. 85, 3676 (2000).

[5] A. Kudrolli and J. Henry, Phys. Rev. E 62, 1489 (2000).

[6] W.A.M. Morgado and E.R. Mucciolo, Physica A 311 (2002) 150.

[7] K. Feitosa and N. Menon, Phys. Rev. Lett. 88, 198301 (2002).

[8] S. McNamara and W.R. Young, Phys. Rev. E 53, 5089 (1996); S. McNamara, Physics of Fluids A 5, 3056 (1993).

[9] I. Goldhirsch and G. Zanetti, Phys. Rev. Lett. 70, 1619 (1993).

[10] R. Brito and M.H. Ernst, Europhys. Lett. 43, 497 (1998); J.J. Brey, M.J. Ruiz-Montero, and D. Cubero, Phys. Rev. E 60, 3150 (1999); T.P.C. Van Noije, and M.H. Ernst, Phys. Rev. E 61, 1765 (2000).

[11] This is also the case of systems exhibiting velocity dependent coefficients of restitution that tend to unity when the initial relative velocity tends to zero.

[12] Schofield and I. Oppenheim, Physica A 196, 209 (1993).

[13] A recent manuscript addresses the equation of state problem for a granular gas: O. Herbst, P. Müller, M. Otto, and A. Zippelius, cond-mat/0402104 (2004).

[14] N.G. van Kampen, Phys. Rep. 124, 69 (1985).

[15] W.A.M. Morgado, I. Oppenheim, Phys. Rev. E 55 (1997) 1940.

[16] N.V. Brilliantov, F. Spahn, J.-M. Hertzsch, T. Pöschel, Phys. Rev. E 53 (1996) 5382.

[17] G. Kuwabara, K. Kono, Jpn. J. Appl. Phys. 26 (1987) 1230.

[18] J.T. Jenkins and S.B. Savage, J. Fluid. Mech. 130, 187 (1983); A. Puglisi, V. Loreto, U. M. Bettolo Marconi, and A. Vulpiani, Phys. Rev. E 59, 5582 (1999); V. Garzó and J.W. Dufty, Phys. Rev. E 59, 5895 (1998).

[19] See references in: H.J. Herrmann, Physica A 313, 188 (2002); H. M. Jaeger, S. R. Nagel, and R. P. Behringer, Rev. Mod. Phys. 68, 1259 (1996); T. Shinbrot and F. J. Muzzio, Nature 410, 251 (2001); Phys. Today 53, 25 (2000).

[20] T. Pöschel and N.V. Brilliantov, cond-mat/0311327; N.V. Brilliantov and T. Pöschel, Phys. Rev. E 61, 2809 (2000).

[21] I. Oppenheim, and N.G. van Kampen, Physica A 196, 231 (1996).

[22] W.A.M. Morgado and I. Oppenheim, Physica A 246, 547 (1997); W.A.M. Morgado and I. Oppenheim, Physica A 252, 308 (1998).

[23] G. Sandri, Ann. Phys. 24 (1963)332; Ann. Phys. 24 (1963) 380.

[24] S.Chapman and T.G.Cowling, The Mathematical Theory of Non-Uniform Gases, Cambridge University Press, Cambridge, 1960.

[25] N.V. Brilliantov and T. Pöschel, Phys. Rev. E 61, 5573 (2000); N.V. Brilliantov and T. Pöschel, Phys. Rev. E 67, 061304 (2003).

[26] A. Astillero and A. Santos, cond-mat/0309220 (2003).

[27] P. K. Haff, J. Fluid Mech. 134 (1983) 401.

[28] V. Garzó and J. Dufty, Phys. Rev. E 60 (1999) 5706; T. Pöschel, N.V. Brilliantov and T. Schwager, Physica A 325, 274 (2003).

[29] J.J. Brey, J.W. Dufty, C.S. Kim, and A. Santos, Phys. Rev. E 58, (1998) 4638; J. M. Pasini and P. Cordero, Phys. Rev. E 63 (2001) 041302.

Received on 10 February, 2004; revised version received on 6 April, 2004

Publication Dates

• Publication in this collection
  04 Nov 2004
• Date of issue
  Sept 2004

History

• Received
  10 Feb 2004
• Reviewed
  06 Apr 2004