Metric nonsymmetric theory of gravitation: the analogue of the theorem of Birkhoff

REGULAR ARTICLES

Metric nonsymmetric theory of gravitation: the analogue of the theorem of Birkhoff

S. Ragusa^I; D. Bosquetti^II

^IInstituto de Física de São Carlos Universidade de São Paulo, C.P. 369 13560-970 São Carlos, SP, Brazil

^IIFaculdade de Tecnologia de Mococa Mococa, SP, Brazil

ABSTRACT

We prove that a spherically symmetric solution of the field equations of the metric nonsymmetric theory of gravitation developed previously is necessarily static.This is the analogue of the well known Birkhoff theorem in general relativity.

Keywords: Nonsymmetric; Birkhoff

I. INTRODUCTION

In previous papers [1-I,II] a metric nonsymmetric theory of gravitation has been developed by one of us and the solution for a spherically symmetric point source was obtained. Of course, the result holds true outside a spherically symmetric material distribution. The theory was shown to be consistent with the four classical tests of general relativity (GR). In [2] the electromagnetic field was included into the theory and the solution for a point charge was obtained. The conservation laws associated to the theory were studied by one of us in [3]. Then [4], we have established the equations governing the interior problem of a static spherically symmetric perfect fluid with a view to a study of stelar equilibrium.

In this paper we show that we have a counterpart of the theorem of Birkhoff of GR, that is, we show that a spherically symmetric solution of the vacuum field equations is necessarily static. We will call this the static theorem. The proof of this result will run along the same lines of GR as presented, for instance, in [5].

The paper is organized as follows. In Sec. II we present the vacuum field equations of the theory and in Sec. III, we prove the static theorem. In Sec. IV we draw our conclusions and highlight future work.

II. THE VACUUM FIELD EQUATIONS

The vacuum field equations of the theory are

and

We use the notation a_(ab) = (a_ab + a_ba)/2 and a_[ab] = (a_ab - a_ba)/2 for the symmetric and antisymmetric parts of a_ab and the notation a_[ab,g] = a_[ab],g + a_[ga],b + a_[bg],a for the curl of a_[ab]. In the first equation

symmetric because the second term is (see (2.10) below) and containing only the symmetric part of the connection, is the analogue of the Ricci tensor. L is the cosmological constant. The next two equations involve the symmetric and antisymmetric parts of g^ab = 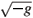g^ab where g = det.(g_ab) and g^ab is the inverse of g_ab as defined by

The second field equation, (2.2), can be solved for the symmetric part of the connection [1-I] giving

with

Here s_ab, symmetric and with determinant s, is the inverse of g^(ab) as defined by

In deriving (2.7) from (2.2) we come across the relation

which can be re-obtained from that equation. One then sees that the second term on the right of (2.5) is in fact symmetric.

Inside the sources of the field the right-hand side of equations (2.1), (2.3) and (2.4) would contain, respectively, the source terms 8pG

_(ab), 4p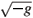Sa and 8pG

_[ab]/L with

where T_ab is the stress tensor and T = g^µnT_µn, and S^a is the fermion number current density

III. SPHERICALLY SYMMETRIC VACUUM SOLUTION: THE STATIC THEOREM

We will then consider the time -dependent spherically symmetric gravitational field satisfying the empty-space field equations (2.1)-(2.4). This may be for example the field outside of a radially pulsating spherically symmetric star. The metric is similar to the one considered in [1,II] but now with the metric components g₀₀, g₁₁ and g_[01] depending on r and t, which we write as

and all other components equal to zero. The non-zero components of the inverse matrix are then

We need also s_ab, whose non-zero components are

The determinants have values

and

With these relations equation (2.8) gives

Let us see the form acquired by the field equations. From the onset we see that (2.4) is identically satisfied. We consider now (2.3). Due to the last relation in (3.2) there are only two non-trivial components of that equation, that is, for a = 0 and a = 1. They are

From (3.4) and the last relation in Eq. (3.2) we have

From these equations we see that the quantity

is a constant, with respect to both space and time. F is the conserved fermionic charge number. From here it follows that the combination

is time independent. From this result it follows that the quantity C in (3.6) is also time independent. It depends only on r and, therefore only C_,r survives in equation (2.7). We have

Using these facts a little calculation will show that besides the connection components written in (1,II-20), which we repeat here for completeness (a^' = a_,r),

there are three additional components which do not vanish. They are (a = a_,t)

They come from

and

when use is made of the time independent relation in (3.10). The relations in (3.13) are of the same form as in GR. Let us see now what are the relations that they will bring about to the field equation (2.1). Putting for short

B = r⁴ + F²

we obtain the following non-trivial four relations, corresponding first to a = b = 0,

then to a = b = 1,

next to a = b = 2,

and finally to a = 0 and b = 1,

All these relations reduce to those of GR [5] when F = 0. From the last one we see that

Therefore, the additional last terms on the left-hand side of both equations (3.15) and (3.16) drop out. As m is time independent it follows from the second relation in (3.1) that this so also for a, that is, it depends only on r, a = a(r). Consequently we are back to the equations we had before in [1-II] with the only difference that g now depends also on t. The solution of these equations goes as in [1-II]. Multiplying (3.15) by a/g and adding the result to (3.16) we obtain, after some algebra [1,II-25],

Integration gives

Therefore,

where

The fact that g(r,t) can depend on time only through a time dependent factor could be guessed before integration because (3.20) tell us that g^'/g is time independent and, consequently, g has to have the form written in (3.22). Using (3.20) in (3.17) we can integrate to obtain r/a, leading to

where M is a constant in space and time and

From (3.23) and (3.24), we obtain

This is the value of the time-independent metric component g₀₀(r) obtained in [1-II]. From (3.22) we see that only the time part of the line element ds² will contain a time dependent coefficient, gdt² = k(t)(r)dt². However, this time dependent factor can be made equal to unity by a change of the time coordinate. In fact it is sufficient to use the new time coordinate given by

to obtain the time independent metric studied in [1,II],

Starting from here and following the same steps of the beginning of this section. we obtain Eq. (3.9) with replacing g,

This tell us that w is also time-independent and given by the same expression as before in [1-II],

This follows from the previous equation, which gives

and Eq. (3.23).

IV. CONCLUSIONS

In this work sequence was given to previous papers [1-4] concerning a metric nonsymmetric theory of gravitation. We have shown that a result similar to the Birkhoff theorem of GR is valid, i. e., that the external field of a time-dependent spherically symmetric system is necessarily static. Thus, for example, the external field of a star pulsating radially is the same of the one of a star at rest, with the same mass M and fermionic charge F.

In [2] the electromagnetic field was included into the theory. It will be interesting to extend the result studied here to the case in which the electromagnetic field is also present. We would then have the counterpart of the Birkhoff theorem known in the Einstein-Maxwell field of GR as presented, for instance, in [5].

These papers will be referred to as I and II, respectively. Equations (1,I-n) and (1,II-n) stand for equations in the corresponding references.

Received on 28 June, 2006

• [1] S. Ragusa, Phys. Rev. D 56, 864 (1997).
• [2] S. Ragusa and D. Bosquetti, Braz. J. Phys. 30, 569 (2000).
• [3] S. Ragusa, Braz. J. Phys. 35, 1020 (2006).
• [4] S. Ragusa and D. Bosquetti, Braz. J. Phys. 36, 576 (2006).
• [5] See for instance, A. Papapetrou Lectures on General Relativity (Dordrecht, Holland, 1974).

Publication Dates

• Publication in this collection
  21 June 2007
• Date of issue
  Dec 2006

History

• Received
  28 June 2006