Magnetic walls in nematic liquid crystals

Magnetic Walls in Nematic Liquid Crystals

M. Simões¹ and A.J. Palangana²

¹ Departamento de Física, Universidade Estadual de Londrina,

Campus Universitário, 86051-970, Londrina (PR), Brazil

²Departamento de Física, Universidade Estadual de Maringá,

87020-900, Maringá (PR), Brazil

Received on 23 November, 2001

In recent published papers it has been shown that the theory about the formation of magnetic walls in the neighborhoods of the Fréedericksz threshold is in profound disagreement with experiments. This finding leads to the development of a new theory for the onset of these structures in this region of magnetic fields. In this paper we present a review of these developments. The previous theory describing these unstable structures claims that the mode with the fastest initial growth will determine the observed properties of these patterns. But, just above the Fréedericksz threshold, there is a region where this leading mode vanishes and, therefore, a homogeneous bending of the director could be detected. This prediction was not confirmed by the experiment, and walls with very well defined wavelength were found. To explain these experimental facts it has been shown that the fastest growing mode can not be defined around the Fréedericksz threshold and, therefore, a new way to compute the observed periodicity must be formulated. The observed wall results from a sum of a continuum and non-sharp distribution of modes in which the null mode is at the center. This work is written in such away that the main conceptual developments can be easily generalized to systems presenting similar behavior.

I Introduction

One of the most outstanding phenomena in out of equilibrium physics is that, even under transient conditions, the onset of very regular and symmetric structures in fluid systems is frequently observed [?]. These kind of phenomena, that have the Rayleigh-Bernard convection as a corn-stone, abound in many different areas and, only to quote few examples, they are regularly found in solid state physics, nonlinear optics, chemistry, and biology. As a rule, it is the internal motion of the matter composing these systems that induces the production of these configurations and, of course, to without such dynamical behavior it would be impossible observe one. Taking this observation as evident by itself one can ask for the behavior of these patterns when their internal fluid flow becomes smaller and smaller, approaching the limit in which the fluid velocity can be neglected. What will be the behavior of the mechanism that produces these structures when this limit is considered? Will continue patterns always appearing or are there critical points in their arising? The study of a physical system where these kind of questions can be formulated, and answered, is the aim of this work. The emergence of magnetic walls [2-5] in nematic liquid crystals(NLC) will be our laboratory for the study of these problems.

Consider, for example, the situation in which a high magnetic field is applied perpendicularly to a homogeneously pre-oriented NLC. A competition occur between the action of the magnetic field and the elastic resistance of the medium; the magnetic field tends to align the director along its direction and the elastic interaction, due to the cohesion of the NLC with the edges of the sample, tends to retain a uniform orientation of the director. For values of the applied field below a critical value, , no distortion arises. For those values of the field which are larger than some textures appear, indicating that the magnetic coupling between the director , and the field , is bigger than the elastic interaction inside the nematic material. When this happens we have the well known Fréedericksz transition that, from the static point of view, has some characteristics of a second order phase transition.

But, the director does not rotate in a homogeneous way. When observed through crossed polarizers, the sample exhibits very regular structures; a set of one-dimensional, periodic and parallel lines extending along the direction of the external magnetic field, the magnetic walls of the NLC. A fundamental element to understand the presence of these lines is the p-symmetry of the director. In the nematic medium the director orientation is double valued (n and -n are equivalent). Therefore, above the Fréedericksz transition the director can bend clockwise or anti-clockwise. This double choice is typical of systems exhibiting a symmetry breaking and, as it is usual in these conditions, two differently orientated portions of the sample can be created. A wall is the continuous bending of the director field connecting these two different configurations: a kink. A typical periodic structure is exhibited in Fig. 1. Despite its importance for the explanation of this symmetry breaking, the p-symmetry cannot explain the astonishing symmetries observed in this figure. The walls extended as right lines along the direction of the external magnetic field and, furthermore, they are periodically distributed along the

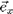direction. They appear in the sample as a one-dimensional and periodic structure. There is not an a priori reason leading to this experimental finding. All that the p-symmetry teach us is that there may be regions with different bending of the director, but it can not explain the symmetries observed in this figure. Therefore, some basic information about the process that build walls are missing.

It was conjectured by Guyon et al. [6] and Lonberg et al. [7] that the elastic properties of the nematic medium are not enough to explain the observed geometry walls. The nematic material is an anisotropic liquid and, at the moment of the walls creation, its internal rearrangement must be taken in to account. The director rotation stimulates the motion of the nematic material and it is this internal motion that gives rise to the one-dimensional and periodic outstanding character of the walls. As a consequence of these investigations, it becomes well established that for high magnetic fields the internal motion of the nematic material, which starts at the moment at which the external magnetic field is turned on, has a decisive role for their construction, being the responsible for their outstanding one-dimensional and periodic character. In fact, with the use of the anisotropic properties of NLC, Guyon et al. [6] and Lonberg et al. [7] have shown that the construction of the walls is possible because the coherent motion of the nematic material driving them, has an effective viscosity which is lower than the one resulting from the matter movement forming any other kind of pattern. That is, the observed periodicity results from a selection mechanism that amplifies to macroscopic scale some well defined fluctuations. If fact, all modes are amplified. But, the central concept of this theory affirms that the final observed profile of these patterns is determined, at the beginning of the process, by the modes having the fastest initial amplification. From now on this mechanism will be referred to as the leading mode principle.

Furthermore, according to the calculations resulting from these ideas, when the Fréedericksz threshold is approached, from the upper side, the coherent internal motion of the nematic material becomes smaller and smaller and there is a point , greater than the Fréedericksz critical point , below which it disappears. Between this point and the Fréedericksz threshold the walls would be absent and the director would have a homogeneous alignment. The region | | < H < | | is known as the forbidden region. So, according to the usual interpretation, in the forbidden region the torque of the external field on the nematic molecules would produce a uniform alignment, and the periodic walls would not be detected.

Nevertheless, there are some theoretical and experimental evidences indicating that, whenever a good image of the physical process behind the origin of these structures is provided, this principle can not give a full explanation to the pattern observed on the magnetic walls [?,?]. In some recent works it has been found that at the neighborhoods of the Fréedericksz critical point the comparison between the predictions of the leading mode principle and experimental facts are in a irreconciliable disagreement [,]. In an experimental investigation, using the twist-bend geometry [,,], we found that, when the Fréedericksz threshold is approached, the emergence of these structures continues [] and, no matter how close the Fréedericksz critical point is approached, a homogeneous alignment of the director has never been found. Moreover, it was observed that the time spent in the construction of these periodic walls diverges as the critical point is approached. Therefore, the predictions of the theory based on the leading mode principle were not confirmed and a forbidden region was not detected by the experiment.

In the sequence, we have proposed a theoretical explanation for this unexpected behavior []. A careful analytical study of the non-linearities involved on the pattern formation at the neighborhoods of the Fréedericksz threshold has been undertaken. It has been shown that, at this region, a unique leading mode can not be clearly defined. In fact, there is a set of neighboring modes, continuously distributed, that grows practically at the same rate. The result of this collective growth is not a homogeneous bending of the director, as predicted by the leading mode principle, but a set of very well defined periodic walls, whose formation tends to spend an infinite time interval when the Fréedericksz threshold is approached.

The aim of this paper is twofold. We will review the theory of the formation of the magnetic walls in the neighborhoods of the Fréedericksz transition and, at the same time, we will examine the question proposed above, by studying an example of patterns' formation in the limiting situation where the fluid flow, that determine the appearing of these out of equilibrium structures, can be made arbitrarily small.

The work is divided in three sections. In the first section, the general theory of the walls formation is presented. In the next one, the leading mode principle is discussed and our experimental results, showing that at the neighborhoods of the Fréedericksz threshold this theory fail, are presented. Finally, at the final section our theory showing how these structures are created at this region, is presented.

II Fundamentals

In order to study the dynamical process leading to the appearance of the magnetic walls, a NLC sample inside a microslide glass with dimensions (a,b,d) that satisfy the relation a b d will be considered. The director is initially uniformly aligned along the 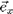direction and an external controlled magnetic field is applied along the direction. Under these conditions we can suppose that the director components will always remain in the plane defined by the direction of the magnetic field and the initial orientation of the director [?], that is

In order to study the NLC dynamics, the so-called Eriksen-Leslie-Parodi (ELP) approach [14-16] is used. The time evolution of the director direction and the motion of the nematic material is given by a set of differential equations composed by the anisotropic version of the Navier-Stokes equation [], the balance of torques equation, and the equation of continuity [,]. The full form and the way by which these equations are handled in the formulation of this problem can be found elsewhere [,,]. As our aim is the obtainment of a non-linear formulation of this problem, some attention will be given to the approximations done on the equations of the ELP approach. The usual approximations make the following assumptions: a) the fluid velocity does not has components along the direction, b) the viscosity dominates the motion of the nematic material and the inertial component can be neglected, c) the conditions prevailing at the borders of the sample have not any decisive influence in the shape of these structures, d) the component of the velocity along the direction of the magnetic field, V_y, is the dominant one and only it needs to be considered [], e) save for the edges of the sample [] the bending of the director will be constant along the direction of the external magnetic field.

Normally, only the linear parts of the equations resulting of these approximations are analytically studied (there are numerical studies of these non-linear equations [,]). Consequently, the walls' amplitude will grow without limit and this approximation leads to a description that is valid at the initial moments of the walls arising. In order to describe the long time behavior of these structures, their saturated profile is needed. So, the choice of the non-linear components that will be retained in our equations will be guided by the following criterion: only those that are decisive for a saturated profile of the walls' amplitude will be maintained.

The Navier-Stokes equation is given by

being r the density of the system,

V

_a the a component of the velocity,

p the pressure and s

_ba the associated anisotropic stress tensor, which depends on the velocity

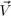
of the fluid, on the bending of the director q, and on its time variation rate

[,,].

The approximation assumed above allows us to consider the problem as two-dimensional. So, the components of the Navier-Stokes describing the motion of the nematic fluid along the 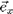and directions are sufficient to describe the walls' phenomenology. Hence, the pressure p can be eliminated from these equations by subtracting one of the components of these equations from another []. Furthermore, we will consider that the velocity of the matter in the sample is such that we can neglect the non-linear term V_b¶_bV_a. Thus,

To further simplify this equation we must remember that the characteristic time involved in the phenomenon in study is so long [] that the viscosity becomes the dominant dynamical parameter of the nematic fluid flow and, therefore, any inertial term can be neglected. Furthermore, using the expressions for the stress tensor given, for example, at the references [?, ?] the above equation becomes

where

and h₁,h₂ and h₃ are the Miesowicz's coefficients, g₁ is the viscosity's coefficients related to rotation of the director (it was assumed that g₂ = -g₁) and, along the direction , it was assumed that q = -(p/d)²q.

Moreover, we also consider that the walls' periodicity along the 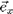direction allows us to Fourier decompose ¶_xV_y and q. That is,

where

= ¶

_t

b

_k. So, Eq. (??) becomes

Consequently,

From this equation, we see how each Fourier component of ¶_tq induces a shear motion of the nematic material, inducing a non null value to the Fourier components of ¶_xV_y. It is important to observe that, through the functions c₁, c₂, c₃ and c₄, given by Eq. (??), Eq. (??) is strongly dependent on q. At this point the usual approach [?] restricted the analysis of the walls formation to the q independent term of this equation. This procedure is valid only when the bending of the director is very small and, consequently, in the first moments, when the leading mode principle is supposed to act. But, when the next order terms are considered, we have

where

and

= (

k

d/p)

² is the reduced wave-vector. This equation shows that, for each

k, there is an angle, j

_o, above which the Fourier component of the bending of the director,

, no more induces a non-null value to the corresponding Fourier component,

a

_k, of the shearing, ¶

_x

V

_y.

Using the same approximations used above, and making the changes

the balance of torques equation,

becomes

Using the result of Eq. (??) we arrive at

where

and

Now, the term q² of Eq. (??) is written in terms of its Fourier components, given by Eq. (??), and the resulting expression integrated in the interval (0, L),giving

where

I

_nt(

b

k

₁

b

k

₂

b

k

₂) represents the terms of order higher than three on

b

_k. The argument of

I

_nt has been written as

b

k

₁

b

k

₂

b

k

₂ to explicitly indicate that it is only at this term that the interaction between the different Fourier components is found. Consequently, in the dynamical equation giving the time evolution of

b

_k, Eq. (??), the interaction between different modes is of fourth order, or higher. So, up to third order the equation giving the time evolution of

b

_k is given by

This equation is integrable, having as solution

which gives the time independent evolution of each mode k. A_o is a constant of integration that may be fixed at t = 0.

III The leading mode and its breakdown

In order to understand the leading mode principle, let us consider the lowest order of Eq. (??), that gives the time evolution of the Fourier component b_k:

In this approximation, we see that b_k would have an exponential growing, and the rate of this growing is determined by the value of t_o. That is, the fastest growing rate of b_k will happen for the smallest t_o. Furthermore, observe that according to Eq. (??), t_o is k dependent. Consequently, each Fourier component b_k will have a different growing rate. The leading mode principle states that the pattern observed in the sample correspond to the Fourier mode with the fastest growing rate; the one with the lowest t_o, which is solution of the equation

This results in a selection mechanism for the parameter k² that, through the minimization of t, is given by k = 0, or by one of the roots of the equation

This selection mechanism has given good results for the regions far above the Fredericks threshold, but as can be easily verified [,] this equation predicts the existence of a region £ h²£ 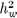, where

in which the selected mode would be characterized by

k

² = 0, that is, the fastest mode would be the homogeneous bending of the director. Furthermore, it can also be shown that for this mode the coherent velocity of the nematic material would be zero.

In order to verify the validity of this approach in this region we have conducted experiments looking for the outputs of the parameters k² and t_o in the neighborhoods of the Fréedericksz transition. A nematic lyotropic mixture of potassium laurate ( KL) , potassium chloride (KCl ) and water, in the calamitic nematic phase, with the respective concentrations in weight percentage: 34.5, 3.0, 62.5 was used. Nematic samples were encapsulated in flat glass microslide (length a = 20mm, width b = 2.5 mm, and thickness d = 0.2mm) from Vitrodynamics. Fig. 1 shows a periodic distortion of with walls formed in the direction of in a polarizing microscope. During the experiment the temperature was controlled at 25 ± 1⁰C. According to the theory presented above we would expect, from Eq. (??), that in the neighborhoods of h²

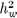, it is obtained

where

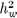was given in Eq. (??). At the same time, as

k

² ® 0, the time t would converge to the fixed value

Summarizing, the above results lead us to believe that as k² ® 0 it would be expected that a graph of k² vs. h² would be a straight line converging to the point 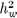. Below this point a homogeneous director bending would be found. In Fig. 2 the results of our measurements are shown. Surprisingly, the walls always exist and a region with homogeneous alignment was never found. In this figure the dotted line gives a picture of this supposed result [].

Furthermore, a graph of t vs. h² would converge, as k² ® 0, to the point t_w calculated above, which is clearly a finite time interval. But, according to our experimental results the time spent with the formation of these structures diverges as the point for which k² ® 0 is approached. We have obtained data so close to this critical point that the corresponding walls only appeared after two or three days of continuum exposition to the magnetic field. Observe that the first point only appears in the curve of k² vs. h². At this point we did not find the formation of any kind of structure in the sample, even after a week of continuous exposure to the magnetic field. Consequently, we are not approaching the point h² = 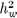. Furthermore, no signal of any kind of homogeneous alignment was found at this point, or below it.

Therefore, it is experimentally evident that the Fréedericksz threshold must be above this point, and we are forced to conclude that the two curves are not approaching the point h² = 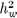, but the Fréedericksz critical point h² = 1. That is, the formation of walls in the upper neighborhoods of the Fréedericksz transition has been detected in a region where, according to the existing theory, these structures would not exist. We have never seen a homogeneous bending of the director and, furthermore, the time taken with the walls' construction became infinite as the critical point was approximated. Furthermore, the final wave number presented by the observed patterns is not the one obtained by the fastest mode of Eq. (??). Indeed, the fastest mode is not even an approximation of the observed result, simply because it predicts the absence of patterns. Our measurement of the wavelength and the time spent with the formation of these objects indicate that these walls are built by the system as soon as the Fréedericksz threshold is exceeded. Moreover, the Lonberg model cannot explain the long time demanded by their construction. Indeed, it is impossible to conceive that there is a coherent motion of matter lasting three days in a viscous medium where the only external force is due to a constant magnetic field. In the neighborhoods of the Fréedericksz threshold the time spent with the constructions of the walls becomes so large that the viscosity of the system would damp any coherent motion of matter. For this reason, we assume that the big random fluctuations existing in the neighborhoods of ?? [?] are driving the birth, and selection, of the observed structures.

IV The collective growth

As the experimental results reported above are in clear contradiction with the predictions of the leading mode principle, it becomes necessary to understand the formation of these walls from another point of view. In order to do it, our first attitude will be to consider the next order approximation of Eq. (??). So, the formation of magnetic walls at the neighborhoods of the Fréedericksz threshold will be examined closely and it will be shown that in this region the statement that says that there is a unique isolated mode determining the physical properties of the observed patterns is rather ambiguous and can not be considered - even as an approximation - for the real physical situation. That is, a large set of states contributes equally to the formation of the magnetic walls in this region.

In this order, the mode that has the leading mode principle can be rewritten as

that becomes Eq. (??) when the third order term is abandoned.

When this equation is applied to Eq. (??) it leads to

where q_o stands for the initial distribution of the mode b_k that, as usual [?, ?], can be found using the equipartition theorem. The behavior of the solution obtained with the Eq. (??), when the magnetic field approaches the Fréedericksz threshold (h²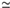 1) is now going to be discussed. An analytical computation shows that around k²» 0 the real solutions of Eq. (??) are given by

where P(h₁, h2, h₃, g₁, h2) is an awkward and non null function that has no influence on the results presented below. From this equation it is easy to see that in the whole interval

where

the unique real solution of Eq. (??) is given by k2 = 0. So, it seems that also in this order we have the presence of a forbidden region. Nevertheless, let us consider the second derivative, (), at t = 0. For it we have found that

From this result, it is easy to see that, at the point h = h_lm, the second derivative is null and, furthermore, it changes sign when this point is crossed. Moreover, in the whole interval 1 £ h²£ , the second derivative is small (it is proportional to h₃⁴) and negative. Hence, as the range of the modes contributing to the walls formation is given by the inverse of (), the usual interpretation that follows from Eq. (??), which says that in the forbidden region the unique mode contributing to the wall's formation is given by = 0, can not be true.

Likewise, a straightforward calculation shows that

Finally, we also have found that

where O() represents the terms of the order of , or higher, that are insignificant. So, exactly at h = h_lm, only the fourth derivative of the growing speed of the director with relation to k, is non-null and it is this value that controls the width of the distribution of modes at this point.

The results exposed in the Eq. (??) to Eq. (??) are graphically exhibited in Fig. 3, where a numerical computation, using the known parameters of the MBBA, for the behavior of [(b)\dot]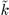, as a function of 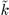, as the point h_lm is approached, is shown. From these figures, we clearly see that, around h_lm, the concept of an isolated mode contributing to the observed periodicity of the walls is meaningless, and a new way to compute the contribution to the final periodicity of the walls must be found.

In order to propose a new way to calculate the walls' periodicity, in the forbidden region, we observe that the periodicity of the walls cannot be understood as a result of the contribution of a unique and isolated mode. It must be supposed that the final walls' periodicity is determined by the long time collective growth of the modes neighboring the mode 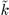= 0. In this case, the natural candidate to fix the participation of each of these modes in the final profile is just the maximum amplitude that each of them can attain. So, it can be assumed that, around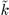 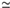0, the final profile q(x) = q(x, t ® ¥) of the walls could be approximated by

where q

_max(

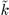
) is given by Eq. (??). However, with the form for q

_max(

k) given by Eq. (??), this integration is probably impossible. As the maximum of q

_max(

k) occurs at

k = 0 , it can be expanded around this point and

is obtained, where

It has been assumed that (

h

² - 1)

² is small, so

where

J

₁(

) is a first kind Bessel function of order 1. As, due to our non-linear approximations, our results can not be extended to the walls nodes and consequently they are only valid for small

x, we can use the approximation

J

₁(

x)

(

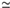
x/2)cos(

x/2) to obtain

With this equation for the profile of the wall along the

direction we can get its wave vector, that is given by

which is just the experimentally found result; a linear relationship between

h

² and

[?]. Furthermore, this expression for

can be substituted in the Eq. (??) to obtain the time spent in the walls' formation, in the forbidden region, as a function of the magnetic field

h. The result is given by

that, as it was experimentally found, diverges when h² ® 1.

V Conclusion

In this work we have studied the behavior of an out of equilibrium dynamical system that presents pattern formation due to the internal motion of its matter, even when the velocity of its fluid flow approaches zero. Contrarily to the usual theory that assumes the existence of a leading mode, has been shown that the results of the leading mode principle, which is the theory that up to now is used to describe their formation [?,?], can not explain its arising in this region. It is known that in the interval 1 £ h²£ , where is given in Eq. (??), the leading mode principle predicts that the fastest mode would correspond to k = 0. This result corresponds to a homogeneous bending of the director and, therefore, to the absence of any texture. As this result was not observed in the experiment, we have here a strong evidence that, at least around the Fréedericksz threshold, the leading mode principle deserves some reformulation. The main result presented by this work states that, in this region, the mode k=0 is the center of a large distribution of modes where each of them gives almost the same contribution to the final profile of the observed walls. In order to obtain a model for the magnetic walls formation, we have supposed that, due to the long time involved in this process, around the Fréedericksz threshold, each mode attains its maximum amplitude. These isolated contributions have been added and the final profile of the periodic walls has been obtained. We have also computed the time spent with the formation of these structures and we have experimentally found that, as the Fréedericksz threshold is approached, this time approaches the infinite.

Acknowledgments

This work was supported by the Brazilian agencies, CNPq and Araucária.

• [1] M. C. Cross and P. C. Hohenberg. Rev. of Mod. Phys. 65, 851 (1993).
• [2] P. G. de Gennes and J. Prost, The Physics of Liquid Crystals, (Clarendon Press, Oxford, 2nd ed., 1993).
• [3] F. Brochard , J. Phys. (Paris) 33, 607 (1972).
• [4] L. Léger, Mol. Cryst. Liq. Cryst. 24, 33(1973).
• [5] M. Simões, A. J. Palangana, and L.R. Evangelista, Braz. J. Phys. 28, 348 (1998).
• [6] E. Guyon, R. Meyer, and J. Salan, Mol. Liq. Cryst. 54, 261 (1979).
• [7] F. Lonberg, S. Fraden, A. J. Hurd, and R. B. Meyer, Phys. Rev. Lett, 52, 1903 (1984).
• [8] G. Srajer, S. Fraden, and R. Meyer. Phys. Rev. A 39, 4828 (1989).
• [9] A. Amengual, E. Hernandes-Gracía, and M. San Miguel, Phys. Rev. E 47, 4151 (1993).
• [10] P.A. Santoro, A.J. Palangana, and M. Simões. Phys. Letters A 243, 71 (1998).
• [11] M. Simões and A. J. Palangana, Phys. Rev. E 60, 3421 (1999).
• [12] J. Charvolin, and Y. Hendrix, J. Phys. (Paris) Lett. 41, 597 (1980).
• [13] M. Simões, A. J. Palangana, A.A. Arrotéia, and P.R. Vilarim, Phys. Rev. E 63, 1707 (2001).
• [14] J. L. Ericksen, Arch. Ratl. Mech. Anal. 4, 231 (1960); 9, 371 (1962).
• [15] F. M. Leslie, Quart. J. Mech. Appl. Math. 19 357 (1966).
• [16] O. Parodi, J. Physique (Paris) 31, 581 (1970).
• [17] L.D. Landau and E. M. Lifshitz. Fluid Mechanics, (Butterworth-Heinemann, Oxford, 1995).
• [18] W. H. de Jeu. Physical properties of liquid crystalline materials, (Gordon and Breach, New York, 1979).
• [19] G. Vertogen and W. H. de Jeu. Thermotropic Liquid Crystals, Fundamentals, (Springer-Verlag, Berlin, 1988).
• [20] M. Simões and A. A. Arrotéia, Phys. Rev. E 59, 556 (1999).
• [21] M. Simões, Phys. Rev. E56, 3061 (1997).
• [22] M. Grigutsch, N. Klöpper, H. Schmiedel, and R. Stannarius, Mol. Cryst. Liq. Cryst. 261, 283 (1995).
• [23] M. Grigutsch, N. Klöpper, H. Schmiedel, and R. Stannarius, Phys. Rev. E 49, 5452 (1994).
• [24] H. E. Stanley, Introduction to Phase Transitions and Critical Phenomena, (Claredon Press, Oxford, 1971).

Publication Dates

• Publication in this collection
  27 Oct 2002
• Date of issue
  June 2002

History

• Received
  23 Nov 2001