Low-energy parabosonic membrane: new critical dimensions and deformed noncommutativity

Low-energy parabosonic membrane: new critical dimensions and deformed noncommutativity

L. Khodja^*; N. Belaloui

Département de Physique, Faculté des Sciences Exactes, Université Mentouri, Route Ain El-Bey, Constantine 25000, Algeria

ABSTRACT

We study a classical perturbative membrane based on the string-limit model and we discuss the consistency of the theory where the closure of the classical constraints algebra is verified. We paraquantize the model (extended string) both in the covariant and the transverse approaches. From the generalized Poincaré algebra, the so-called Poincaré (para) algebra, we show that the space-time critical dimensions D are related to the order of the paraquantization Q by the relation D = 3+24/Q. The symplectic structure is generalized for the paraquantum case and applied to the parabosonic membrane coupled to a constant 3-form field. This leads to a deformed noncommutative relations at the ends of the membrane (extended string) describing a geometry which might be called a q-noncommutativity.

Keywords: Membranes, q-deformation, Noncommutativity.

I. INTRODUCTION

In the last three decades, a new revolutionary theory known as string theory has emerged and seemed to be a serious candidate for the fundamental theory of nature by the fact that it was the alone theory which seemed reconcile the classical theory of general relativity at large distance scales with the standard model of quantum particle physics at short distance scales.

It has been shown that there are five consistent quantum superstring theories which can be constructed by choosing different sets of fields on the string world-sheet. These are the types I, IIA, IIB, heterotic E₈⊗E₈ and SO(32) theories.

The multiplicity of these theories added with the fact that the supergravity is an eleven dimentional theory while the consistent ten-dimensional superstring theories give microscopic models for quantum gravity goes against the successful of the string theory.

In 1995, a remarkable new idea caused a substantial change in the dominant picture of superstring theory as the main candidate for fundamental description of the world. Indeed, all the known consistent string theories seem be special limit cases of a more fundamental theory which has been baptized M-theory [1, 2], and which seems to be most naturally described in eleven dimensions. The string has also lost its position as the main candidate. It is important, however, to notice that the string theory contains dynamical objects of several differential dimensionalities; in particular, a two-dimensional string excitation known as membrane gives some interesting properties like the eleven-dimensional supermembrane which let us think to a microscopic description of the eleven-dimensional supergravity through a quantization of a supermembrane.

Before the emergence of the eleven-dimensional M-theory, much more attention was given to the ten-dimensional theories (superstrings) at the expense of the eleven-dimensional ones because of the misreading of the eleven-dimensional space-time properties.

Another intringuing fact emerging in this context is the connection between string theory and noncommutative geometry [3]. There has been a flurry of activity in analysing noncommutativity in strings and membranes, in particular, those derived in either string coupled to the two-form or the membrane coupled to the three-form [4-11].

Unlike the string theory, the study of the membrane theory is more involved than the analogue study in the string case, since the equations to be resolved are nonlinear [12].

The specificity of the membrane is the fact that the Lagrangian has no Weyl invariance [12], which suggests that some of the basic techniques in string theory such as the conformal mapping are not available. In string theory the critical dimension such as D = 26 is well-known, it is for example related to Lorentz invariance in the light cone gauge. The critical dimension of the membrane has mainly been discussed with regard to its spectrum [13, 14], to the truncated versions of the BRST [15] or the Lorentz algebra [16], where the D = 27 emerges as a necessary condition. Notice however that, it is not clear wether the dimension of embedding space plays as crucial a role for membranes as it does for strings. A natural way to find a critical dimension for the membrane is to relate this latter to the string theory via dimensional reduction [17]. In this string limit, it is natural to obtain D-1 = 26 for the bosonic membrane, since one of the D dimension in the membrane is absorbed by the gauge freedom [16, 18-23].

The purpose of this paper is to investigate the paraquantum extension of a bosonic membrane. The paraquantization, as a generalization of the quantization, was first introduced by Green [24]. Indeed, in 1950, Wigner [25] demonstrated that, for satisfying the wave particle duality, which is a direct consequence of the Heisenberg equations of motion, the set of the usual bilinear canonical commutation relations is a particular solution. Based on trilinear commutation relations, the paraquantization consists in a generalization of the creation-annihilation operators algebra for the bosons and the fermions. We note also that the paraquantization is characterized by a parameter Q, the order of the paraquantization, such that Q = 1 corresponds to the ordinary quantization [26].

A first study of a paraquantum string theory was done by F. Ardalan and F. Mansouri [27]. This study is based on the particular manner in which the center of mass variables of the string are to be handled. Indeed, these authors impose on the center of mass coordinates and the total energy momentum operators of the string x^µ, p^µ to satisfy ordinary commutation relations. This is done by the choice of a specific direction in the paraspace of the Green components, characterized by the anzatz x^µ(β) = x^µδ_β1 and p^µ(β) = p^µδ_β1, where x^µ(β) (resp. p^µ(β)) are the Green components of x^µ (resp. p^µ). This requires relative paracommutation relations between the center of mass coordinates and the excitation modes of the string which are exclusively anomalous bilinear commutation relations in terms of the Green components. Because of the separation of β = 1 and β ≠ 1 in the precedent anzatz, these bilinear commutations relations can not be rewritten in trilinear commutation relations form which are the basis of the paraquantization.

A second study of the parastring theory is proposed [28, 29], where the paraquantization is done by requiring that both the center of mass variables and the excitation modes of the string verify paraquantum commutation relations. Indeed, in this study, paraquantizing the string theory consists in reinterpreting the classical bosonic and fermionic string variables x^µ(σ,τ) , P^ν(σ',τ) , and ψ^ρ ( σ",τ) as operators satisfying the paraquantum trilinear commutation relations (τ is a time like evolution parameter, while the parameter σ labels points on the string).

Notice however that in these two approaches, the resulting parabosonic (resp. paraspinning) string theories are Poincaré invariant if the dimension D of the space-time and the order Q of the paraquantization are related by the expressions D = (resp. D = ).

The paper is organized as follows: In section II, a classical perturbative bosonic membrane theory based on the study of a string-limit model is reviewed, the closure of the constraints algebra is discussed. In sections III and IV, we paraquantize this model both in the covariant and in the transverse approaches, where from the closure of Poincaré (para) algebra, a relation between the spacetime dimension D and the order of the paraquantizations Q is derived implying in this other possibilities of the critical dimensions other than D = 27. In section V, we discuss the interacting bosonic membrane and the symplectic structure of the string in B-field, the paraquantization appears as a q-deformation of the noncommutative relations, which we baptize as a q-noncommutative relations. The last section is devoted to discussion.

II. REVIEW OF A CLASSICAL PERTURBATIVE BOSONIC MEMBRANE

II.1 Action

An open membrane is a two dimensional object which when it is moving in (D-1) spatial dimensions sweeps out a three dimensional world-volume (in D dimensional space-time) parametrized by σª, a = 0, 1, 2. We use a metric with a signature ( -,+,...,+) in the target space and x^µ( τ,σ,ρ) a membrane coordinates. The Polyakov action for the bosonic membrane is then given by [30]:

where

and µ,ν = 0,1,...,D-1. T_m describes the tension of the membrane.

To simplify the study of the membrane dynamics, we are leading to use the symmetries of the theory. Unfortunately, unlike the case of the classical string, where there are three components of the metric and three continious symmetries (two diffeomorphism and one scale symmetries) leading to a complete specification of the metric by gauge fixing, for the membrane, we have six independent components and only three diffeomorphism symmetries and in particular no scale symmetry.

As a consequence, the membrane equations of motion are intrinsically non linear, which do not allows one to obtain their general solutions. Some special solutions were considered in the literature. A particular sector of the solution is the study of the low-energy limit of small radius for the cylindrical membrane where we take the σ² = ρ direction of the membrane to be wrapped around a circle with radius R ( 0 < ρ < 2πR) .

We look for solutions of the membrane coordinates x^µ( τ,σ,ρ) with a judicious ansatz introduced by [23] as follows:

We consider d = 2 reparametrization invariant truncation of the coordinates ( a = ( α,2) ) [23, 31]:

and of the metric

=0,1 where W^µ is a normed constant field.

Notice however that in [31], the perturbative theory is considered up to the order ε².

In the begining, the h^ab metric possess 6 independent components but in this writing of h^ab, it remains 5 independent components while the sixth is fixed by the gauge h²² = 1+g^αβ Φ _α Φ _β to satisfy the condition deth^ab = detg^αβ.

The action takes then the form

where D_αZ^µ= ∂_αZ^µ+Φ _αW^µ, and the tension of the membrane T_m reduces to the scale of the string tension T_s, through the relation

where l_p is the Planck's length.

Notice here that the r reparametrization is hidden by its absence in the action. However, the field Φ _α plays the part of ρ with respect to the hidden membrane symmetry which became an additional symmetry to the extended string and which takes the form [23, 32]

This additional symmetry may be seen as an additional gauge invariance of the string in the spirit of gauged Wess-Zumino-Witten models [32].

Finally, this action is invariant under Poincaré, local and Weyl symmetries, with also the additional gauge invariance with the parameter Λ.

The canonical momenta for the fields Z^µ, g_αβ, Φ _α are respectively:

It is clear that, while is a genuine momentum, and are the primary constraints of the theory. The first one is equivalent to the vanishing of the symmetric energy-momentum tensor:

and the second is the same as the equation of Φ _α given by

One can then set the three equations of constraints of the theory as follows:

which represent the three restrictions on the world-volume metric through the previous detailed constrained Hamiltonian analysis of the free Polyakov membrane [31].

The classical Hamiltonian is expressed as:

where

The time evolution of the field Z^µ and momenta is governed by:

This latter with the particular choice corresponding to Φ₀ = 0 leads to an ordinary form of the Poisson brackets (P.B) as the following:

where now and later

Notice here that the P.B for the induced field Φ₀ is not verified, this case is identical to the electrodynamic field A₀ in QED, where the Lorentz gauge is used.

From the P.B (2.1-2.1), one can easily show that the constaints (2.1-2.1) satisfy the following closed algebra

the set of these relations is equivalent to the closure of the constraints algebra of the membrane given in [11].

Now, as it is mentioned above, it is possible to use the two dimentional world-sheet symmetry: The Weyl symmetry to fix the gauge g^αβ= η^αβ, which is one of the most advandage of the model.

One can then adopt the usual strategy in string theory with respect to the Virasoro algebra by regrouping the previous constraints in a compact writing, this is done by the substitution of the constraint χ₃ in the two others. We proceed as follows:

Let us redefine the momentum as

where W^µν is a symmetric constant tensor verifying

We can then write

where φ₃ is the condition given by the equation φ₃ = W^µD₁Z_µ≡ 0

It is easy to see that

which correspond to the well-known form of the constraints in classical string theory.

The equation of motion of the field Z^µ is

we consider the Neumann boundary conditions (for a closed string)

Substituting (7) in the equation (13), with the boundary conditions (14), the general solution coincides with the ordinary equation of the usual string which is given by:

we can also rewrite the P.B relations (2.1-2.1) in terms of modes as follows

resolving the equation (7), the equation (12) is rewritten in the form = 0 where:

let us now introduce the corresponding Virasoro generators L_n and defined through the Fourier transformations of the previous constraints:

In term of modes, L_n and take the following forms:

where

and which verify the usual form of the classical Virasoro algebra.

One can also see that the Poincaré generators are unchanged and verify the classical closed algebra.

III. COVARAINT PARAQUANTIZATION AND ALGEBRAS CLOSURE

III.1 Covaraint paraquantization of the model

The paraquantization of the theory is carried out by reinterpreting the classical dynamical variables as operators satisfying the following trilinear relations:

In terms of modes:

where the operators A^µ, B^µ, C^µand D^µ are given by:

the other remaining trilinear relations are null.

The Green components of a paraboson A can usually be expressed as [24, 26]:

where is a parameter of paraquantization and e^α are elements of a Clifford algebra satisfying the following relations

then, the decomposition of the dynamical variables can be written in the form

In terms of the Green components, the trilinear commutation relations (55-62) transform to the bilinear ones of an anomalous case:

all the remaining other relations are of the type: [A^µ(α), B^ν(α)] = 0 or [ A^µ(α), B^ν(β)] ₊ = 0 for a ≠ β.

III.2 Poincaré and constraints (para) algebras

In the parastatistical case, the constraint generators L_n and have the same writing as in the classical case with an adequate symmetrization, one can then write:

One can easily verify that the Virasoro algebra is unchanged except the central charge which takes the form c_Q= Q( D-1) /12 through the relations:

In the same way, and with also an adequate symmetrization, we can define the angular momentum generators associated to the Poincaré transformations as follows:

These generators with the total momentum verify a closed Poincaré (para) algebra given by:

Where the usual relation [p^µ,p^ν] = 0 is broken.

We can show also that the physical state conditions are invariant under Lorentz transformations, we can see this through the relations

IV. TRANSVERSE PARAQUANTIZATION AND CRITICAL DIMENSIONS

IV.1 Transverse paraquantization

Now that we have explored the paraquantization of a low-energy limit of small radius for the cylindrical Polyakov membrane in the covariant gauges imposing the Virasoro conditions as subsidiary constraints on physical states, there is still a residual gauge symmetry that remains after setting the gauges and can be used to make further specific gauge choices. Indeed, by making a particular non covariant choice, it becomes possible to solve the constraint equations, and describe the theory in a Fock space that describes physical degrees of freedom only.

This particular choice correpond to impose additional gauge conditions which will be non covariant but quite convenient.

• The first one is as follows: The substitution of the constraint χ₃ in the two others χ₁ and χ₂ in (12) in order to reduce the problem to a string theory, is decribed by the following specific and convenient choices:

which reduces the model to an ordinary parabosonic closed extended string moving in (D-1) flat spacetime.

• The second one corresponds to the usual light-cone gauge given by the equations:

in which the Virasoro constraints equations will be solved to obtain the dynamical variables , , , p⁺, and p^I where , and = 2πα.

These latters verify the following trilinear relations:

where the operators A, B, C, D, E and F are given by:

and the other remaining trilinear relations are null.

In terms of Green components, one can write the following anomalous bilinear relations:

all the remaining other relations are of the type [ A^(α), B^(β)] = 0 or [A^(α), B^(β) ] ₊ = 0 for α ≠ β.

IV.2 New critical dimensions

In order to check the consistency of this paraquantum model, let us construct the Lorentz generators and check their commutation relations. The only source of the anomaly is the [ M^I-,M^J-] commutator which must be zero. From the relation (3.2) one can write the following expression for the M^I- generators (we have choosen W^D-1 = 0):

where the paraquantum form of the modes are imposed as:

(a is the usual ordering constant, and a = ã)

and where the transverse part of the generators L_n and are given by

Now, using the following expressions:

where ζ(s) is the well-known Zeta-Riemann function defined as:

By the use of the set of the trilinear relations (85-96), one can see that the following relations hold

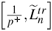= 0. It is not difficult to reduce the expression (4.2) of M^I- to the following form:

which coincides exactely with those imposed in [28].

Now, using the relations (85-100) and (111), straightforward calculations give

which is zero under the conditions

In particular, one can have parabosonic membranes with the critical dimensions D = 27, 15, 11, 9, 7, 6, 5 and 4 respectively in the orders Q = 1, 2, 3, 4, 6, 8, 12 and 24.

This result, which can be rewritten in the form D-1 = 2+, reflect the relation D'= 2+ for the parabosonic string [27-29], since, as it was yet mentioned above, a string is derived from a dimensional reduction of the membrane, so that, one of the D dimension in the membrane is absorbed by the gauge freedom.

V. PARABOSONIC MEMBRANE IN A CONSTANT BACKGROUND FIELD

As it was briefly discussed in the introduction, let us examine the study of the bosonic membrane propagating in the presence of a three form field A_µνρ. As it was mentioned above, here, we are led to the problem of finding a simpler system which captures the essential features of the open membrane dynamics in a constant 3-form field. Since the direct paraquantization of the membrane is difficult, so far, we are led to work in the same sector of solutions used above in the free case: the low-energy limit of small radius for the cylindrical membrane.

The problem is reduced to the study of the extended string propagating in the presence of a 2-form field B_µν. Since, in the quantum case, the noncommutativity comes from the 2-form field B_µν which is coupled to the string world-sheet, one may wonder what result will be obtained in the paraquantum case?

Let us consider the Polyakov action of a bosonic membrane in the presence of a constant field [8, 34]:

Applying the above d = 2 reparametrization invariant truncation of the coordinates (3) with the writing (2.1-2.1) of the metric h^ab, the action (19) will be reduced to the expression

where

Now, in the gauge Φ₀ = 0 used in the second section, the expression of the canonical conjugate momentum is given by:

The Z^µ variation of the action leads to the equation of motion (37), with the new boundary conditions

(l = π for an open string and 2π for a closed one)

One can obtain the solution in the following form

for the open case and

for the closed one.

In the following, we will consider only the open case.

Let us first recall that, in the ordinary case, the quantization of Z^µ(τ,σ) has to be different from the usual canonical commutation relations for a free fields, because, the standard equal time commutation relations are inconsistent with the boundary conditions (23). One has to modify the quantization in a consistent manner. Indeed, while the commutation relations are the standard ones for any point in the interior of the open extended string, at the two end points, we find that the space time coordinates are noncommutative.

Here, in the paraquantum case, we will do the same in the following, where again, one has to modify the paraquantization in a consistent manner.

The usual way to quantize a classical system is to start with the symplectic structure on the phase space. Applying the procedure of [2.1] in the paraquantum case, one find that the symmertized symplectic form is

where

In terms of a Green components, we can write

where (2α'= 1)

with M^µν= h^µν -B^µρ B^ν _ρthese imply the following anomalous bilinear relations

which are equivalent to the following trilinear commutation relations for the modes

where A^µ = or p^µ and the other remaining trilinear relations are null.

It is not dificult to see that the corresponding trilinear commutation relations for the field Z^µ and their momentum conjugate , can be given as follows

where

and

notice that in terms of a Green components, we can write

where the q-deformed commutator is defined in [13] as

One can finally conclude that the inconsistency of the standard equal time commutation relations (for a free fields) with the boundary conditions (23) in addition to the general approach of the paraquantization lead to a two times modified commutation relations at the two end points of the open extended string (noncommutativity and q-deformation) which we baptize: q-noncommutativity, and a one time modified commutation relations for the interior of the string (q-deformation)

VI. DISCUSSION

In this paper, we have developed a string-limit model of a classical perturbative bosonic membrane and demonstrated the closure of the constraints algebra for a specific choice of a gauge. We have paraquantized this model. It is observed that in the covariant approach, the Poincaré algebra is maintained, except the [ p^µ,p^ν] commutator which is modified as a trilinear relation [ p^µ,[ p^ν,p^ρ] ₊] = 0.

For the second approach, based on the transverse gauge with the additional one (80-82), different possibilities for the space-time dimensions D, other than D = 27, are found for the parabosonic membrane through the relation D = 3+ . We employ the symplectic structure of the string generalized to the paraquantum case to study the interacting parabosonic membrane in the constant B-field. We have also modified the basic P.B in order to establish a consistency of the boundary conditions with the basic P.Bs. The modification consisted of a q-deformed noncommutativity of the two ends of the extended string and a q-deformation for the interior. It would be very intreresting to notice that the paraspinning extension of this work is an investigation which suggests itself. Indeed, one expects that the truncation used can be equally applied to the parasupermembrane action which would give a supersymmetry version for the model considered. From the result D = 3+ for the parabosonic membrane sector, one expects new possibilities of critical dimensions for the parasupermembrane [14].

References

[1] E. Witten, Nucl. Phys. B 443, 85 (1995).

[2] P.K. Townsend, arXiv:hep-th/9612121.

[3] N. Seiberg and E. Witten, JHEP 9909, 032 (1999).

[4] E. Bergshoeff, D. S. Berman, J. P. van der Schaar and P. Sundell, Nucl. Phys. B 590, 173 (2000).

[5] S. Kawamoto and N. Sasakura, JHEP 0007, 014 (2000).

[6] A. Das, J. Maharana and A. Melikyan, JHEP 0104, 016 (2001).

[7] Ken-Ichi Tezuka, Eur. Phys. J. C 25, 465 (2002).

[8] S. Gangopadhyay, Phys. Lett. B 659, 399 (2008).

[9] C. S. Chu and P. M. Ho, Nucl. Phys. B 550, 151(1999).

[10] F. Ardalan, H. Arfaei, M.M. Sheikh-Jabbari, Nucl. Phys. B 576, 578 (2000).

[11] R. Banerjee, B. Chakraborty and K. Kumar, Nucl. Phys. B 668, 179 (2003).

[12] H. Kamo and T Sohkawa, Prog.Theor. Phys. 57, 1749 (1977).

[13] K. Kikkawa and M. Yamasaki, Prog. Theor. Phys. 76, 1379 (1986).

[14] K. Fujikawa and J. Kubo, Phys. Lett. B 199, 75 (1987).

[15] J. Kubo, Phys. Lett. B 202, 315 (1988).

[16] U. Marquard and M. Scholl, Phys. Lett. B 227, 227 (1989).

[17] G. T. Horowitz and L. Susskind, J. Math. Phys. 42, 3152 (2001).

[18] I. Bars, C. N. Pope and E. Sezgin, Phys. Lett. B 198, 455 (1987).

[19] U. Marquard and M. Scholl, Phys. Lett. B 209, 434 (1988).

[20] U. Marquard, R. Kaiser and M. Scholl, Phys. Lett. B 227, 234 (1989).

[21] I. Bars, Nucl. Phys. B 343, 398 (1990).

[22] P. Bozhilov, Mod. Phys. Lett. A 13, 2571 (1998).

[23] A. A. Deriglazov, Nucl. Phys. B 597, 299 (2001).

[24] H. S. Green, Phys. Rev. 90, 270 (1953).

[25] E. P. Wigner, Phys. Rev. 77, 711 (1950).

[26] Y. Ohnuki, S. Kamefuchi, Quantum Field Theory and parastatistics, (Springer-Verlag, 1982).

[27] F. Ardalan and F. Mansouri, Phys. Rev. D 9, 3341 (1974).

[28] N. Belaloui and H. Bennacer, Czech. J. Phys. 53, 769 (2003).

[29] N. Belaloui and H. Bennacer, Czech. J. Phys. 54, 621 (2004).

[30] W. Taylor, Rev. Mod. Phys. 73, 419 (2001); P. A. Collins and P. W. Tucker, Nucl. Phys. B 112, 150 (1976); P. S. Howe and P. W. Tucker, J. Phys. A 10, L155 (1977); A. Sugamoto, Nucl. Phys. B 215, 381 (1983).

[31] L. Smolin, Phys. Rev. D 57, 6216(1998).

[32] I. Bars and C. Kounnas, Phys. Rev. D 56, 3664 (1997).

[33] M. B. Green, J. H. Schwarz and E. Witten, Supersting Theory, Vol.I, (Cambridge University Press, 1987).

[34] M. J. Duff, arXiv:hep-th/9611203.

[35] O. W. Greenberg and A. K Mishra, Phys. Rev. D 70, 125013 (2004).

[36] L. Khodja and N. Belaloui, in progress.

(Received on 25 June, 2009)

Publication Dates

• Publication in this collection
  11 Feb 2010
• Date of issue
  Dec 2009

History

• Received
  25 June 2009