Abstract
A particular class of strong non-Markovian stochastic processes have been studied by using a characteristic functional technique previously reported. Exact results for all moments and the whole Kolmogorov hierarchy are presented. The asymptotic scaling of the non-Markovian stochastic process has been characterized in terms of the long-range correlated noise appearing in the correponding stochastic differential equation. A generalized Wiener process has therefore been completely characterized, its power spectrum and fractal dimensions have been studied and its possible connection with the q-statistics has been pointed out.
Non-Markovian processes with long-range correlations: fractal dimension analysis
Manuel O. Cáceres* * Also Investigador Independiente en el CONICET. Electronic mail: caceres@cab.cnea.edu.ar
Centro Atómico Bariloche and Instituto Balseiro
CNEA, and Universidad Nacional de Cuyo
Av. Ezequiel Bustillo Km 9.5
8400 San Carlos de Bariloche, Río Negro, Argentina
Received 07 December, 1998
A particular class of strong non-Markovian stochastic processes have been studied by using a characteristic functional technique previously reported. Exact results for all moments and the whole Kolmogorov hierarchy are presented. The asymptotic scaling of the non-Markovian stochastic process has been characterized in terms of the long-range correlated noise appearing in the correponding stochastic differential equation. A generalized Wiener process has therefore been completely characterized, its power spectrum and fractal dimensions have been studied and its possible connection with the q-statistics has been pointed out.
I Introduction
For a non-Markovian stochastic process (s.p.) X(t), it is well known that its complete characterization demands the knowledge of the whole Kolmogorov hierarchy, i.e.: the m-time joint probability distribution P[X(t1); X(t2);···; X(tm)] for all m, or equivalently all the m-time moments áX(t1)X(t2)···X(tm)ñ or cumulants ááX(t1)X(t2)···X(tm)ññ . Only when partial knowledge of the s.p. is required the 1-time probability distribution P[X(t1)] is enough, this is the case when 1-time moments of the process áX(t)mñ are needed [1, 2, 3]. This fact can easily be visualized using the functional calculus, i.e.: knowing P[X(t1)] is equivalent to the knowledge of the characteristic function áexp ikX(t1)ñ . But in order to know the whole Kolmogorov hierarchy the knowledge of the characteristic functional GX([k(t)]) = áexp ò ik(t)X(t)dtñ is required, which of course is a much more complex object [5]. The notation GX([k(t)]) emphasizes that G depends on the whole test function k(t), not just on the value it takes at one particular time tj. The convergence of the integral is accomplished because the functions k(t) may be restricted to those that vanish for sufficiently large t. On the other hand the possibility of having a closed expression for the characteristic functional allows us to find the Kolmogorov hierarchy by quadrature. Very recently[6] a generalized Wiener process X(t)-with natural boundary conditions-has been defined and its complete characterization has been given in terms of the arbitrary characteristic functional of the noise Gx ([k(t)]).
In the present paper we are concerned with the asymptotic analysis of the non-Markovian effects-on X(t)-induced by a long-range correlated noise, i.e.: when the s.p. X(t) is defined through the equation:  being x(t) a Gaussian non-white noise. Here we will characterize a stationary short-range noise correlation by an exponential function
being x(t) a Gaussian non-white noise. Here we will characterize a stationary short-range noise correlation by an exponential function
On the contrary a stationary long-range noise correlation will be characterize by a power-law function
We remark that a white-noise force can be reobtained from (1) in the limit q® 0; while a constant force can be obtained from (2) in the limit m® 0. In order to study different scaling regimes, in this paper we will only be interested in t and q finites.
II A strong non-Markovian process
The equation of motion of a 1-dimensional Brownian particle in a generalized (infinite) medium has a Wiener-like stochastic differential equation (SDE)
where x(t) Î Re is an arbitrary time-dependent random force characterizing the medium (the noise). When x(t) is a zero-mean Gaussian white noise, i.e.: áá x(s1)x(s2) ññ = d(s1-s2), Eq.(3) is the usual Wiener's SDE. In this case the s.p. X(t) characterizes the position of a Brownian particle[5]. Let us now generalize the noise x(t), with t Î [0,¥), to be a zero-mean Gaussian noise characterized by some short or long-range correlation. Therefore its functional will be
where the correlation function áá x(s1)x(s2) ññ is given by (1) or (2) and G2 is proportional to the intensity of the noise. Non-Gaussian statistics can also be worked out in a similar manner [6].
Due to the fact that the s.p. X(t) is non-Markovian, there is not a simple partial differential equation available for its 1-time probability distribution, and the problem is even more complicated if we want to know the 2-times joint probability distribution[7], for example in order to calculate correlation functions. We remark that in this paper we do not make use of any partial differential equation, this is why our characteristic functional approach is of value.
By using proposition 3 of reference[6], it follows that the characteristic functional of the s.p. X(t) is
here X0 is the initial condition and k0 is a functional of Z(t) given by
Therefore all m-time moments of the s.p. X(t) follow from m-th order functional differentiation, i.e.:
see appendixappendix for the explicit calculation of the second cumulant of X(t). On the other hand, the Kolmogorov hierarchy can immediately be obtained by quadrature from the functional (4). In general we can invert the characteristic functional by introducing the n-dimensional Fourier transform
We remark that (4) is an exact result which allows us to get a complete characterization of the non-Markovian s.p. X(t). For example the 1-time probability distribution P( X[t1]) is given in terms of GX( [Z(t)]) evaluated with the test function Z(t) = k1d(t-t1). From (4) and (7) we see that, to know the 1-time probability distribution, we must calculate the integral
A. Short-range noise correlation
Let us exemplify the use of the short-range correlation (1). In this case (8) gives
From this expression it is simple to see that due to the non-Markovian effect (q ¹ 0) the 1-time characteristic function GX(k, t) º á expikX(t) ñ does not have the familiar Wiener's scaling:
Which would imply in the s.p. X(t) the scaling
Only asymptotically for long-times, from (9) the following relation is held
Then we can conclude that a short-range correlated noise does not affect-in the long time regime-the universal Wiener scaling (11) [i.e.: only induces weak non-Markovian effects on X(t)].
B. Long-range noise correlation
From now on we will only be interested in strong non-Markovian effects. Thus, let us now use the long-range correlation (2). In this case (8) gives for 0 £ m ¹ 1,2
For m = 1 we get
and for m = 2 reads
If 0 £ m £ 1 from these expressions it is simple to see that due to the long-range effect of the noise, the 1-time characteristic function GX(k1, t1) º á expikX(t1) ñ does not have, even at long times, Wiener's scaling. If the noise power-law parameter m belongs to the values m Î [0,1), we see from (13) that a different long-time asymptotic scaling is obtained: slong(Lt)® L 2-mslong(t). Then from (4) the 1-time characteristic function fulfills the asymptotic long-time scaling (with X0 = 0)
which implies in the s.p. X(t) the (anomalous) super-diffusion asymptotic scaling
Then we can conclude that a long-range correlated noise induces a strong non-Markovian effect which changes the long-time asymptotic scaling of s.p. X(t). If m = 1 there are logarithmic corrections, only if m > 1 Wiener's scaling is reobtained in the asymptotic long-time regime.
C. Spectral of the random fluctuations of the s.p. X(t)
From (17) let us define the parameter  . Then, after the transient, in the asymptotic long-time regime the s.p. X(t) fulfills the scaling X(L t)® L HX(t). Note that from our non-Markovian generalized Wiener process, the parameter H is bounded to the values
. Then, after the transient, in the asymptotic long-time regime the s.p. X(t) fulfills the scaling X(L t)® L HX(t). Note that from our non-Markovian generalized Wiener process, the parameter H is bounded to the values  . From this relation it is possible to estimate the power spectrum of the s.p. X(t) in a simple way[8]. In order to calculate the spectral representation of the random fluctuations let us fix some L and define a s.p. Y(t) in the following way:
. From this relation it is possible to estimate the power spectrum of the s.p. X(t) in a simple way[8]. In order to calculate the spectral representation of the random fluctuations let us fix some L and define a s.p. Y(t) in the following way:
Adopting the Fourier notations
for example and
and  , etc. Let us now compute FY(f, T) using its scaling relation (18)
, etc. Let us now compute FY(f, T) using its scaling relation (18)
Then it follows
so the spectral density is given by
and in the limit T® ¥ we get
Now because Y(t) is nothing more than a properly rescaled version of X(t), their spectral densities must coincide. Take for example L º 1, so SY(f) = SX(f). Hence, it follows the relation
Now, formally putting f = 1 and replacing 1/L by f in (24) the desire result is obtained
This expression is the spectral representation of the random fluctuations of a s.p. having the scaling property: L -HX(Lt) = X(t).
Our non-Markovian s.p. fulfills in the long-time regime the scaling (17), then it follows that its corresponding spectral behaves asymptotically like
Thus, only approaching the limit m® 1 the fluctuations of our s.p. X(t) approaches Brownian's noise spectral ®1/f2. On the other hand, after the transient, and in the asymptotic long-time regime the non-Markovian s.p. X(t) gets Wiener's spectral only if m > 1, see (13)-(15).
D. Fractal dimension of the record X(t)
The 1-time probability distribution P( X[t]) of our non-Markovian generalized Wiener process can be obtained from (4) and (7), leading to the exact result
where s(t) is given in (9) for a short-range model, and by (13)-(15) for a long-range correlated model [strong non-Markovian case]. In Eq. (27) X0 is the initial condition of the s.p. X(t), so to be precise P(x, t) is in fact a conditional probability distribution. In general due to the non-Markovian effects this distribution does not satisfy-at short times-a scaling relation, only in its asymptotic long-time regime a scaling law is reached, which in fact is analogous to the scaling relation of self-similar objects. However there is an important difference, the distribution (27) with s(t) given by (13) [for the weak non-Markovian case use (12)] has an asymptotic scaling with different ratios in time and in position. Because of this fact, it is very important to take into account the concept of self-affinity[9]. In fact the probability distribution of our s.p. X(t) is related (asymptotically) to the concept of statistically self-affine objects[9].
The fractal dimension of self-affine fractal objects is not uniquely defined, but fortunately the box dimension can be evaluated "mechanically'' for a set of points such as the record of our strong non-Markovian generalized Wiener s.p. X(t). If N(L , a, t) is the number of "boxes'' of width (in time) Lt and length (in space) L a needed to cover the record, and if this number scale with L in the form N(L , a, t) ~ L-DB we say that DB is the box dimension of the record. To calculate this fractal dimension we closely follow Feder's arguments[9]. Let the time-span of the record be T, then we need T/Lt segments of length Lt to cover the time axis. Now, let the scaling be X(Lt) = LH X(t), then it follows that
thus in each segment the range of the record is of the order DX(Lt) = LH DX(t) and we need a stack of LH DX(t)/L a boxes of height L a to cover that range. Therefore the number of boxes to cover the set is of the order
which leads to the (local) box counter fractal dimension[9] DB = 2-H . Now, from the asymptotic scaling (17) and the definition  we get, for our strong non-Markovian s.p. the box dimension
we get, for our strong non-Markovian s.p. the box dimension
Note that in this argument we have used boxes that were small with respect to both the length of the record T and the range of the record, thus the relation  holds in high-resolution, so this is a local fractal dimension1
1
It should be pointed out that in Feder's argument L is supposed to be a small parameter. So in order to apply this argument to our non-Markovian
s.p. we must assume that we have allowed the
s.p. to run for a long time so that any transient has disappeared,
t >> t. Therefore the portion of the record
X(
t) (time-span of the record
T) that we want to measure is in fact in the long-time regime, so it fulfills the asymptotic scaling (17).
. In the case m = 0 we obtain a ballistic behavior (highly persistent record DB = 1). On the contrary, in the limit m® 1 the s.p. X(t) approaches Wiener's box counter fractal dimension
holds in high-resolution, so this is a local fractal dimension1
1
It should be pointed out that in Feder's argument L is supposed to be a small parameter. So in order to apply this argument to our non-Markovian
s.p. we must assume that we have allowed the
s.p. to run for a long time so that any transient has disappeared,
t >> t. Therefore the portion of the record
X(
t) (time-span of the record
T) that we want to measure is in fact in the long-time regime, so it fulfills the asymptotic scaling (17).
. In the case m = 0 we obtain a ballistic behavior (highly persistent record DB = 1). On the contrary, in the limit m® 1 the s.p. X(t) approaches Wiener's box counter fractal dimension 
Owing to this analysis we can conclude that in the asymptotic long-time regime, t>>t, our non-Markovian s.p. can be mapped to the fractional Brownian motion[10] (fBm) with  , in according with the persistent behavior of the fBm. Here persistence means that if the motion has been in an increasing direction during a period t, then it is expected to continue to increase for a similar period of time. This fact is in total agreement with the idea of a strong correlated stochastic force x(t) appearing in the SDE
, in according with the persistent behavior of the fBm. Here persistence means that if the motion has been in an increasing direction during a period t, then it is expected to continue to increase for a similar period of time. This fact is in total agreement with the idea of a strong correlated stochastic force x(t) appearing in the SDE  , see also the appendixappendix for the exact calculation of the correlation á á X(t1)X(t2) ñ ñ .
, see also the appendixappendix for the exact calculation of the correlation á á X(t1)X(t2) ñ ñ .
To be more precise let us here calculate a normalized correlation function of future increments [X(t)-X(0)] with past increments [ X(0)-X(-t)]
From (46) it is possible to show that (for 0 < m ¹ {1,2})
Therefore if 0 £ m < 1, past increments are correlated with future increments, i.e.: a long-range correlated noise with m Î [0,1) induces infinitely long-run correlations in the s.p. X(t) like in the persistent fBm (anomalous super-diffusion). On the contrary if m > 1 the normalized correlation function C(t) goes to zero in the limit t® ¥, in agreement with a Wiener-like behavior.
It is also possible to see, using that the noise x(t) is symmetric and adopting the initial condition X(0) = X0 = 0 in (42), that the variance of an arbitrary increment of s.p. X(t) is given by [for 0 < m ¹ {1,2} and assuming t1£ t2]
Thus, for large t2-t1 such that t2-t1 >> t and if the noise parameter m Î [0,1), we see that á[X(t2)-X(t1)] 2ñ increases with time as ~ (t2-t1)2-m in agreement with the picture of a persistent fBm, i.e.: a long-range correlated noise x(t) induces an anomalous power-law behavior in the variance of the increments of our s.p. X(t). If the noise parameter is m > 1 we reobtain-in the asymptotic long-time regime-the Wiener result á [ X(t2)-X(t1)] 2 ñ ~ | t2-t1|.
It is important to remark that our analytical approach can also be extended to the case when the noise x(t) is also non-Gaussian and non-white. The interplay between both effects is an interesting phenomena to be studied (non-Gaussian vs. strong non-Markovian effects), which is currently under investigation. Note that the same type of long-run fluctuations are also expected for the generalized Orstein-Uhlenbeck process-in presence of a strong correlated noise-this case can also be worked out in a similar way[6, 11].
E. Fractal divider dimension of X(t)
Another fractal dimension that can be evaluated "mechanically'' is the divider dimension along a curve to measure its length. For self-similar fractal curves such as coastlines this fractal dimension can be estimated from the behavior of its total length L ~ d1-D, where d is the "length'' of the rule[9]. The measured length, of a random walk path in the x, t-plane, with a rule of length d, placed such that it covers a time step Lt gives a contribution to the length
where the last equality was written by virtue of the statistical self-similar scaling DX(Lt) = LH DX(t). Here, as before, a measures the scale in the x-axis. Then, depending on the magnification in the x-axis the behavior of d as a function of L will be different. Using a small a, the dominant behavior is d ~ LH. Then the number of segments along the time axis is
where the last equality was written by virtue of the small a dominant behavior d ~ LH. Therefore the total length will have the behavior
from which the divider fractal dimension reads[9, 8] D = 1/H. Because in the asymptotic long-time regime our s.p. X(t) fulfills the scaling (17), we obtain for X(t) the fractal local divider dimension2 2 As we pointed out in the previous section, in order to apply Feder's argument to our non-Markovian s.p. we ought to assume that any transient has disappeared, so the portion of the record X( t) (time-span T) that we want to analyze fulfills the scaling (17).
A result which, in the limit m® 1 is in agreement with Wiener's divider dimension D® 2. In the opposite limit m = 0 the expected ballistic behavior is obtained.
III Perspectives in the framework of Tsallis-statistics
A. Anomalous diffusion
In recent years there have been some interest in relating non-extensive entropies with the phenomena of anomalous diffusion. The starting point is the definition of a q-entropy[12] (in a continuous representation):
where k is a positive constant (such that in the limq®1k® kB is the Boltzmann constant) and x is an arbitrary d-dimensional vector. Thus under the normalization condition of probability 1 = òr(x) dx, and the definition of a generalized mean value energy á (x)ñq º ò
(x)ñq º ò (x) rq(x) dx = Eq (q-expectation value), the maximization of Sq[r(x)] allows to obtain a generalized thermodynamics which conserves Legendre's structure [13]. The definition of the q-entropy (36) can also been used in the context of stochastic processes. We should remark that (36) is the definition of a generalized (equilibrium) q-entropy, therefore in (36) it should be understood that the distribution r(x) is related with a stationary measure. In fact this is the concept which was used when studying irreversible thermodynamics in the neighborhood of its equilibrium distribution[14].
(x) rq(x) dx = Eq (q-expectation value), the maximization of Sq[r(x)] allows to obtain a generalized thermodynamics which conserves Legendre's structure [13]. The definition of the q-entropy (36) can also been used in the context of stochastic processes. We should remark that (36) is the definition of a generalized (equilibrium) q-entropy, therefore in (36) it should be understood that the distribution r(x) is related with a stationary measure. In fact this is the concept which was used when studying irreversible thermodynamics in the neighborhood of its equilibrium distribution[14].
In order to study systems far away from equilibrium the approach is quite different. For instead it is possible to use (36) as the starting point in the definition of the probability transition r(x) (hopping of length |x1-x2| = x) in a random walk scheme. These hopping transitions can be of the short or long-range class. A short-range hopping transition can be obtained by using the well-posed optimization procedure [15]. Nevertheless, this is not the case if we want to find a long-range hopping transition, as the one proposed by Lévy [16]. It is here, where the concept of q-entropy comes into the approach, to be able to give an unified picture concerning short or long-range hopping transitions, from a single optimization procedure. The question may be put in the following way: can Lévy's stable3 3 They are called stable distributions because the addition of N of such variables preserve the same probability distribution. distributions (r(x) ~ x-1-g , 0 < g < 2) be obtained form a simple constraint in the context of the optimization technique? The answer is yes, but only if a generalization of the entropy is used.
Define the generalized constraint  , then applying the variational principle to Sq[r(x)] upon the normalization condition on r(x) and the constraint
, then applying the variational principle to Sq[r(x)] upon the normalization condition on r(x) and the constraint  ; the resulting hopping probability distribution is (in d-dimension)
; the resulting hopping probability distribution is (in d-dimension)
where a and b are the variational Lagrange parameters[17]. For large x this hopping transition has a Lévy stable form, then we can identify (in any dimension) q = (3+g)/(1+g).
In the context of the random walk theory, the Lévy parameter g can be mapped with the Hausdorff-Besicovitch fractal dimension of the set of points visited by the random walk (thus 0 < g < d). These requirements determine that the value of q must satisfy: (3+d)/(1+d) < q < (2+d)/d, which in 1-dimension give 1 < q < 3 (a result which was also obtained in the context of the analysis of the fluctuations in irreversible thermodynamics[14]).
Going one step further it is possible to study the temporal evolution of a Markovian random walk in the context of q-entropies[18]. To be more precise, let P(s, n) be the 1D random walk probability to be at site s in its n-th step. This is nothing more than a Markovian chain in a regular infinite domain. Then P(s, n) fulfills the recurrence relation
which can immediately be solved4
4
Equation (38) can be rewritten by defining the auxiliary generating function:
, for |
z| < 1. Multiplying (38) by
zn and summing from
n = 1 to ¥ we get
by using the Fourier inversion of  , i.e.:
, i.e.:
where  is the Fourier transform of the random walk initial condition P(s, n = 0). From (39) it is simple to see that all the information concerning the evolution of the random walk is contained in the function
is the Fourier transform of the random walk initial condition P(s, n = 0). From (39) it is simple to see that all the information concerning the evolution of the random walk is contained in the function  , which is just given in terms of the Fourier transform of the hopping transition. Then it is possible to see that if the hopping transition is of the long-range type: r(x) ~ x-1-g (i.e.: its Fourier transform is the Lévy stable definition
, which is just given in terms of the Fourier transform of the hopping transition. Then it is possible to see that if the hopping transition is of the long-range type: r(x) ~ x-1-g (i.e.: its Fourier transform is the Lévy stable definition  , none of the random walk moments
, none of the random walk moments  are defined. This is so because this class of hopping transition has not an intrinsic length scale, this fact can easily be seen through the non-analyticity, around k = 0, of the Fourier transform
are defined. This is so because this class of hopping transition has not an intrinsic length scale, this fact can easily be seen through the non-analyticity, around k = 0, of the Fourier transform  .
.
In the context of the q-statistics we would like to characterize the evolution of these moments avoiding these intrinsic divergencies. In particular we can be interested in characterize the q-expectation random walk variance á s(n)2 ñ q, and for example we would like study under which conditions (values of q), for large n, the central limit theorem applies. Invoking a generalized Levy-Gnedenko Markov convolution the result in 1D gives[18]
where  and
and  are well behaved functions, showing a divergency for q = 5/3, and kT is related to a thermal energy. Thus measuring the q-expectation variance (40), can provide a possible experimental verification of the q-statistics.
are well behaved functions, showing a divergency for q = 5/3, and kT is related to a thermal energy. Thus measuring the q-expectation variance (40), can provide a possible experimental verification of the q-statistics.
Naturally the existence of non-Markovian correlations (in the random walk) could modify the predicted critical exponents (40). Therefore it is very important to know exact non-Markovian solutions [as the ones presented in previous sections] in order to analyze possible generalizations of (40), by considering non-Markovian effects in the random walk.
Strong non-Markovian processes, like the one characterized in section II.B, but also taking into account large-excursion hopping transitions-as the one characterized by a Lévy distribution-can be worked out in our approach and they are under investigation.
B. Irreversible Thermodynamics
In the context of q-entropies, Onsager's reciprocity relations were proved by using linear Markov processes (regression theorem) and the concept of q-expectation values[14], therefore it could be of interest to study its non-Markovian generalization.
If a friction term -hX is added to (3), and we allow the Gaussian random force x(t) to be a long-range correlated noise, this type of Gaussian Langevin-like equation can also be worked out, in a similar way, as we have presented here[11]. Thus, an open problem can be to study the N-dimensional linear stochastic dynamics
where á á xj(t1)xl(t2) ñ ñ have long-range correlations as in (2). This type of model could help in understanding irreversible thermodynamics which takes into account long-range fluctuations. Thus providing another possible scenario where the application of the q-statistics can be of value.
IV Discussions
A generalized non-Markovian Wiener stochastic process X(t)-with natural boundary condition-was completely characterized in terms of its functional GX([Z(t)]). Two models of correlated noises have been worked out, particular stress has been put in long-range correlations á á x(t1)x(t2) ñ ñ , like in (2), giving rise to anomalous super-diffusion. This fairly general method is based upon knowing the characteristic functional of the noise Gx ([k(t)]), which in the present paper has been assumed to be Gaussian (generalizations to non-Gaussian statistics can also be worked out in our approach). Any m-time moment of the s.p. X(t) follows straightforwardly by taking functional derivative of GX([Z(t)]), see (6).
One of the questions addressed in this paper has been the characterization of the spectrum and the fractal dimensions of our strong non-Markovian particle in a generalized medium, i.e.: in presence of a long-range correlated noise. If the noise parameter m Î [0,1), past increments of the s.p. X(t) are correlated with future increments, so a long-range correlated noise induces infinitely long-run correlations in the s.p. X(t) like in the persistent fBm (super-diffusion with  .
.
Using our approach, the medium can be represented by an arbitrary correlated random force x(t), [additive noise appearing in the SDE (3)]. The present analytical formulation provides a systematic starting point to obtain higher-order moments and also to compute the whole Kolmogorov hierarchy.
We remark that there is not limitation in the exact calculation of any higher-order moment of our non-Markovian process. In the present paper we have used a functional technique to solve a problem with natural boundary conditions, the application of this method to problems with non-natural boundary condition is under investigation[19]. Also in order to study anomalous super-diffusion, a possible connection with the q-statistics has been pointed out.
Acknowledgments
M.O.C thanks CONICET (grant PIP n.4948) and to Pedro A. Pury for fruitful discussions.
References
-
[1]
- K. Ishii and K. Kitahara, Prog. Theor. Phys. 68, 665 (1982). [2]
- A. Morita, Phys. Rev. A 41, 754 (1990). [3]
- M. Gitterman, Phys. Rev. E 52, 303 (1995), and reference therein. [4]
- A. Compte and M.O. Cáceres, "Fractional Dynamics in Random Velocity Fields'', Phys. Rev. Lett. 81, 3140 (1998). [5]
- N.G. van Kampen, in: Stochastic Processes in Physics and Chemistry, Second Edition, (North-Holland, Amsterdam,1992). [6]
- M.O. Cáceres, A.A. Budini, J. Phys. A Mat. & Gen. 30, 8427 (1997). [7]
- J.M. Sancho and M. San Miguel, in : Noise in Nonlinear Dynamical Systems, Vol.1, Chap.3, Cambridge University Press, Eds. F. Moss, and P.V.E. McClintock, (1989). [8]
- D. Saupe, in: The Science of Fractal Images, Chap. 2, Eds. Heinz-Otto Peitgen and Dietmar Saupe, (Springer-Verlag, Berlin, 1988). [9]
- J. Feder, in: Fractals, (Plenum Press, London, 1989). [10]
- B.B. Mandelbrot and J.W. van Ness, SIAM Review 10, 422 (1968). [11]
- M.O. Cáceres, "Stochastic Harmonic Potential Driven by Long-range Correlated Noises'', submitted (1998). [12]
- C. Tsallis, J. Stat. Phys. 52, 479 (1988). [13]
- C. Tsallis, "Some Comments on Boltzmann-Gibbs Statistical Mechanics '', Chaos, Solitons and Fractals 6, 539 (1995), and references therein. [14]
- M.O. Cáceres, Physica A 218, 471 (1995). [15]
- E.W. Montroll and M. Shlensinger; J. Stat. Phys. 32, 209 (1983). [16]
- P. Lévy; in: Théorie de láddition des variables aléatoires, (Guthier-Villars, Paris, 1937). [17]
- (a) P.A. Alemany and D. Zanete, Phys. Rev. E 49, R956 (1994); (b) P.A. Alemany, PhD. Thesis, Instituto Balseiro, (1995). [18]
- C. Tsallis, S.V.F. Levy, A.M.C. Souza, and R. Maynard, Phys. Rev. Lett. 75, 3589 (1995); erratum Phys. Rev. Lett. 77, 5442 (1996); M.O. Cáceres and C.E. Budde, Phys. Rev. Lett. 77, 2589 (1996). [19]
- A.A Budini and M.O. Cáceres, "The Generalized Wiener Process II: Finite Systems'', J. Phys. A Mat. & Gen. (submitted 1998).
s.p.X(t)
Let us now study the correlation function á áX(t1)X(t2) ñ ñ , which can be calculated in an exact way by using functional derivatives as in (6), from (4) we get
Without loss of generality we now assume that t1£ t2, then we get
so using the definition (8) we can write
1. Short-range
For the particular case of a Gaussian short-range correlated noise the result gives
which of course in the limit q® 0 goes to Wiener's result: á á X(t1)X(t2) ñ ñ = G2min(t1,t2). Note that due to the non-Markovian character (if q ¹ 0) of the s.p. X(t), both times are always present in this non-stationary second cumulant. If t1 >> q and t2 >> q such that t2-t1 > 0, the non-Markovian signature of the s.p. can still be seen in the transient appearing in (45), which gives rise to a small q-correction of the form  . Nevertheless in the asymptotic limit t1, t2® ¥ the dominant term is linear. This means that, in the asymptotic long-time regime, the non-Markovian character of the s.p. X(t) will be erased when the correlation of the noise is of the short-range class.
. Nevertheless in the asymptotic limit t1, t2® ¥ the dominant term is linear. This means that, in the asymptotic long-time regime, the non-Markovian character of the s.p. X(t) will be erased when the correlation of the noise is of the short-range class.
2. Long-range
For the particular case of a Gaussian noise x(t) with a long-range correlation like the one in (2), the behavior is quite different, and gives rise to anomalous super-diffusion. From (44) the result, for 0 < m ¹ {1,2}, assuming as before that t1£ t2, gives
In the asymptotic long-time regime t1 >> t and t2 >> t, such that t2-t1@ O(t), and if the noise parameter is m Î [0,1) we see that the two-point second cumulant (46), increases in time with a power-law ~ ( t12-m+t22-m) . Thus, a long-range correlated noise induces a super-diffusion behavior in the cumulant á á X(t1)X(t2) ñ ñ . Note that both times are always present in this anomalous non-stationary correlation function. Only if the noise parameter is m > 1 we reobtain, in the asymptotic long-time regime, the linear (Wiener) result á á X(t1)X(t2) ñ ñ µ min(t1, t2).
In general the increments of our s.p. X(t) are not statistical independent, as it is-of course-required by a fundamental theorem that says: if the increments of any s.p. are independent therefore the s.p. is a Markov one (the reverse is not true!).
Now, taking the Fourier transform  , etc. ; with the help of the convolution theorem and the geometric series representation, we get
, etc. ; with the help of the convolution theorem and the geometric series representation, we get
Then  can be obtained from the expansion coefficients of
can be obtained from the expansion coefficients of  in power of z.
in power of z.
- [1] K. Ishii and K. Kitahara, Prog. Theor. Phys. 68, 665 (1982).
- [2] A. Morita, Phys. Rev. A 41, 754 (1990).
- [3] M. Gitterman, Phys. Rev. E 52, 303 (1995),
- [4] A. Compte and M.O. Cáceres, "Fractional Dynamics in Random Velocity Fields'', Phys. Rev. Lett. 81, 3140 (1998).
- [5] N.G. van Kampen, in: Stochastic Processes in Physics and Chemistry, Second Edition, (North-Holland, Amsterdam,1992).
- [7] J.M. Sancho and M. San Miguel, in : Noise in Nonlinear Dynamical Systems, Vol.1, Chap.3, Cambridge University Press, Eds. F. Moss, and P.V.E. McClintock, (1989).
- [8] D. Saupe, in: The Science of Fractal Images, Chap. 2, Eds. Heinz-Otto Peitgen and Dietmar Saupe, (Springer-Verlag, Berlin, 1988).
- [9] J. Feder, in: Fractals, (Plenum Press, London, 1989).
- [10] B.B. Mandelbrot and J.W. van Ness, SIAM Review 10, 422 (1968).
- [12] C. Tsallis, J. Stat. Phys. 52, 479 (1988).
- [13] C. Tsallis, "Some Comments on Boltzmann-Gibbs Statistical Mechanics '', Chaos, Solitons and Fractals 6, 539 (1995),
- [14] M.O. Cáceres, Physica A 218, 471 (1995).
- [15] E.W. Montroll and M. Shlensinger; J. Stat. Phys. 32, 209 (1983).
- [16] P. Lévy; in: Théorie de láddition des variables aléatoires, (Guthier-Villars, Paris, 1937).
- [17] (a) P.A. Alemany and D. Zanete, Phys. Rev. E 49, R956 (1994);
- [18] C. Tsallis, S.V.F. Levy, A.M.C. Souza, and R. Maynard, Phys. Rev. Lett. 75, 3589 (1995);
appendix
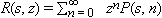 , for |
, for |Publication Dates
-
Publication in this collection
17 Sept 1999 -
Date of issue
Mar 1999
History
-
Received
07 Dec 1998




















































