Abstract
Some properties of the ux-line lattice in conventional and high-Tc superconductors are reviewed, with particular stress on phenomenological theories, nonlocal elasticity, irreversible magnetization curves, and inuence of the specimen shape on the electromagnetic response.
a02v32n3
The Vortex Lattice in Conventional and High-Tc Superconductors
Ernst Helmut Brandt
Max-Planck-Institut für Metallforschung, D-70506 Stuttgart, Germany
Received on 28 February, 2002
Some properties of the ux-line lattice in conventional and high-Tc superconductors are reviewed, with particular stress on phenomenological theories, nonlocal elasticity, irreversible magnetization curves, and inuence of the specimen shape on the electromagnetic response.
I. Introduction
After the discovery of superconductivity in 1912 by Heike Kamerlingh-Onnes in Leiden, it took almost 50 years until this fascinating phenomenon was understood microscopically, when in 1957 Bardeen, Cooper and Schrieffer established the BCS theory. But long before this, there were powerful phenomenological theories, which were able to explain most electromagnetic and thermodynamic observations on superconductors, and which are very useful also today [1,2,3]. The London theory of 1935 is particularly useful for the description of the high-Tc superconductors, which were discovered in 1987 by Bednorz and Müler. The Ginzburg-Landau (GL) theory of 1951 is quite universal; it contains the London theory as particular limit and predicts that superconductors can be of type-I (with positive energy of the wall between normal conducting and superconducting domains) or of type-II (with negative wall energy, pointing to an instability).
The penetration of vortices into type-II superconductors was predicted first by A. A. Abrikosov when he discovered a two-dimensional periodic solution of the Ginzburg-Landau (GL) equations. Abrikosov correctly interpreted this solution as a periodic arrangement of flux lines, the flux-line lattice (FLL). Each flux line (or fluxon, vortex line) carries one quantum of magnetic flux F0 = h/2e = 2.07 ×10-15 Tm2, which is caused by the supercurrents circulating in this vortex. The magnetic field peaks at the vortex positions. The vortex core is a tube in which the superconductivity is weakened; the position of the vortex is defined by the line at which the superconducting order parameter vanishes. For well separated or isolated vortices, the radius of the tube of magnetic flux equals the magnetic penetration depth  , and the core radius is somewhat larger than the superconducting coherence length x [1,2,2], see Fig. 1. With increasing applied magnetic field, the spacing a0 of the vortices decreases and the average flux density
, and the core radius is somewhat larger than the superconducting coherence length x [1,2,2], see Fig. 1. With increasing applied magnetic field, the spacing a0 of the vortices decreases and the average flux density  increases, one has
increases, one has  = 2 F0 /
= 2 F0 / for the triangular FLL, see Fig. 2. The flux tubes then overlap such that the periodic induction B(x,y) is nearly constant, with only a small relative variation about its average
for the triangular FLL, see Fig. 2. The flux tubes then overlap such that the periodic induction B(x,y) is nearly constant, with only a small relative variation about its average  . With further increase of
. With further increase of  also the vortex cores begin to overlap such that the amplitude of the order parameter decreases until it vanishes when
also the vortex cores begin to overlap such that the amplitude of the order parameter decreases until it vanishes when  reaches the upper critical field Bc2 = m0 Hc2 = F0 /(2px2), where the superconductivity disappears. Fig. 3 shows profiles of the induction B(x,y) and of the order parameter |y(x,y)|2 for two values of
reaches the upper critical field Bc2 = m0 Hc2 = F0 /(2px2), where the superconductivity disappears. Fig. 3 shows profiles of the induction B(x,y) and of the order parameter |y(x,y)|2 for two values of  corresponding to flux-line spacings a0 = 4
corresponding to flux-line spacings a0 = 4 and a0 = 2
and a0 = 2 .
.
The periodic solution which describes the FLL exists when the GL parameter k =  /x exceeds the value 1/
/x exceeds the value 1/ (this condition defines type-II superconductors) and when the applied magnetic field Ba = m0 Ha ranges between the lower critical field Bc1 = m0 Hc1 » F0 ln(
(this condition defines type-II superconductors) and when the applied magnetic field Ba = m0 Ha ranges between the lower critical field Bc1 = m0 Hc1 » F0 ln( k) /(4p
k) /(4p 2) (where
2) (where  = 0) and Bc2 (where
= 0) and Bc2 (where  = Ba = Bc2). For |Ba| < Bc1 the superconductor is in the Meissner state, which expels all magnetic flux, forcing B º 0 inside the superconductor. More precisely, for Ba < Bc1 [and in type-I superconductors with k < 1/
= Ba = Bc2). For |Ba| < Bc1 the superconductor is in the Meissner state, which expels all magnetic flux, forcing B º 0 inside the superconductor. More precisely, for Ba < Bc1 [and in type-I superconductors with k < 1/ for Ba < Bc = F0/(
for Ba < Bc = F0/(  px
px )], the applied magnetic field penetrates into a surface layer of thickness
)], the applied magnetic field penetrates into a surface layer of thickness  . For a superconducting half space at x > 0 one has B(x) = Ba exp(-x/
. For a superconducting half space at x > 0 one has B(x) = Ba exp(-x/ ). For a long strip with rectangular cross section (|x| £ a = 40
). For a long strip with rectangular cross section (|x| £ a = 40 , |y| £ b = 0.4a) and with Ba along y, Fig. 4 shows that in this surface layer both B(x,y) and the screening current density J(x,y) =
, |y| £ b = 0.4a) and with Ba along y, Fig. 4 shows that in this surface layer both B(x,y) and the screening current density J(x,y) =  Ñ×B(x,y) (flowing along z) are sharply peaked in the corners, favoring the nucleation and penetration of vortices in form of quarter loops at the four corners of the strip [4,5].
Ñ×B(x,y) (flowing along z) are sharply peaked in the corners, favoring the nucleation and penetration of vortices in form of quarter loops at the four corners of the strip [4,5].
In long slabs or cylinders, with increasing parallel field Ha > Hc1, vortices penetrate and the inner induction  increases monotonically. The magnetization in this longitudinal geometry is defined as M =
increases monotonically. The magnetization in this longitudinal geometry is defined as M =  /m0 -Ha, Fig. 5. The negative magnetization -M initially increases linearly, M = - Ha (Ha = Ba/m0) for Ha £ Hc1 (Meissner state); at Ha = Hc1, -M decreases sharply since flux lines start to penetrate; and when Ha is increased further, -M decreases approximately linearly until it vanishes at Hc2. The area under the magnetization curve -M(Ha) is m0
/m0 -Ha, Fig. 5. The negative magnetization -M initially increases linearly, M = - Ha (Ha = Ba/m0) for Ha £ Hc1 (Meissner state); at Ha = Hc1, -M decreases sharply since flux lines start to penetrate; and when Ha is increased further, -M decreases approximately linearly until it vanishes at Hc2. The area under the magnetization curve -M(Ha) is m0 , where Bc = m0Hc = F0 /(
, where Bc = m0Hc = F0 /( pxl) = Bc2/(
pxl) = Bc2/( k) is the thermodynamic critical field. In superconductors with k = 1/
k) is the thermodynamic critical field. In superconductors with k = 1/ (this case is almost exactly realized in pure Niobium) the three critical fields coincide, Hc1 = Hc = Hc2.
(this case is almost exactly realized in pure Niobium) the three critical fields coincide, Hc1 = Hc = Hc2.
The GL theory originally was derived for temperatures T close to the superconducting transition temperature Tc, where  µ x µ (1-T/Tc)-1/2 diverges. But practically the GL picture is a good approximation at all temperatures 0 < T < Tc, in particular in impure superconductors with short electron mean free path. One usually assumes the temperature dependences
µ x µ (1-T/Tc)-1/2 diverges. But practically the GL picture is a good approximation at all temperatures 0 < T < Tc, in particular in impure superconductors with short electron mean free path. One usually assumes the temperature dependences  (T) »
(T) »  (0)(1 t4)-1/2 (with t = T/Tc) and Hc(T) » Hc(0)(1t2), yielding x(T) » x(0)[(1+t2) / (1t2)]1/2.
(0)(1 t4)-1/2 (with t = T/Tc) and Hc(T) » Hc(0)(1t2), yielding x(T) » x(0)[(1+t2) / (1t2)]1/2.
At low inductions
Bc2 and large k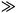 1, the properties of the vortex lattice may be calculated from London theory, to which the GL theory reduces when the magnitude |y| of the GL function y is nearly constant. In the London limit, B(x, y) is the linear superposition of the fields of isolated vortices; the London expressions for B(x, y) and for the energy apply thus also to nonperiodic arrangements of vortices. The London theory was further extended to curved vortices and to anisotropic superconductors. At larger
1, the properties of the vortex lattice may be calculated from London theory, to which the GL theory reduces when the magnitude |y| of the GL function y is nearly constant. In the London limit, B(x, y) is the linear superposition of the fields of isolated vortices; the London expressions for B(x, y) and for the energy apply thus also to nonperiodic arrangements of vortices. The London theory was further extended to curved vortices and to anisotropic superconductors. At larger  > 0.25 Bc2 or smaller k < 2, the GL theory has to be used. Analytic GL solutions are available only for the periodic FLL near Bc2, but not for a distorted FLL or at lower
> 0.25 Bc2 or smaller k < 2, the GL theory has to be used. Analytic GL solutions are available only for the periodic FLL near Bc2, but not for a distorted FLL or at lower  .
.
Expanding the energy of the superconductor with respect to small displacements of the vortices from their ideal lattice positions, one obtains the elastic moduli of the vortex lattice. As opposed to the local elasticity of atomic lattices, the elasticity of the vortex lattice is nonlocal [3], i.e., the energy of compressional and tilt deformations is strongly reduced when the wave vector k of the strain field is large, k >  -1, see Sct. 4.
-1, see Sct. 4.
II. Results from London Theory
The London theory may be formulated by minimizing the sum F of the potential energy of the magnetic field B(r) and the kinetic energy of the supercurrent density J(r) =  Ñ × B(r),
Ñ × B(r),
with respect to B = Ñ × A. This yields the homogeneous London equation B - 2 Ñ2B = 0 or J = -
2 Ñ2B = 0 or J = -
A. Parallel vortices
In the presence of vortices one has to add singularities which describe the vortex core. For straight parallel vortex lines along  one thus gets the modified London equation
one thus gets the modified London equation
Here rn = (xn, yn) are the two-dimensional (2D) vortex positions and d2(r) = d(x) d(y) is the 2D delta function. This linear equation may be solved by Fourier transform using ò exp(ikr) d2 k = 4p2 d2(r) and ò exp(ikr) (k2 + -2)-1 d2 k = 2pK0( |r| /
-2)-1 d2 k = 2pK0( |r| / ). Here K0(x) is a modified Bessel function with the limits K0(x) » -ln(x) for x
). Here K0(x) is a modified Bessel function with the limits K0(x) » -ln(x) for x  1 and K0(x) » (p/ 2x)1/2 exp(-x) for x
1 and K0(x) » (p/ 2x)1/2 exp(-x) for x 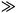 1. The resulting magnetic field of any arrangement of parallel vortices is the sum of individual vortex fields centered at the positions rn,
1. The resulting magnetic field of any arrangement of parallel vortices is the sum of individual vortex fields centered at the positions rn,
see Fig. 1. The energy F2D of this 2D arrangement of vortex lines with length L is obtained by inserting Eq. (2) into (1). Integrating over the delta function one finds that the London energy is determined by the magnetic field values at the vortex positions,
This expression shows that the energy is composed of the self-energy of the vortices (terms m = n) and a pairwise interaction energy (terms m ¹ n). To avoid the divergence of the self-energy one has to cut off the logarithmic infinity of B at the vortex centers rn by introducing a finite radius of the vortex core of order x, the coherence length of the GL theory. This cutoff may be achieved by replacing in Eq. (4) the distance rmn = |rm - rn | by  mn = (
mn = (  + 2x2 )1/2 and multiplying by a normalization factor » 1 to conserve the flux F0 of the vortex. This analytical expression suggested by Clem [6] for a single vortex and later generalized to the vortex lattice [7], is an excellent approximation, as was shown numerically [8] by solving the GL equation for the periodic FLL in the entire range of
+ 2x2 )1/2 and multiplying by a normalization factor » 1 to conserve the flux F0 of the vortex. This analytical expression suggested by Clem [6] for a single vortex and later generalized to the vortex lattice [7], is an excellent approximation, as was shown numerically [8] by solving the GL equation for the periodic FLL in the entire range of  and k, for 0 £
and k, for 0 £  £ Bc2 and k ³ 1/
£ Bc2 and k ³ 1/ .
.
B. Curved vortices
Arbitrary 3D arrangements of curved vortices at positions rn(z) = [xn(z), yn(z),z] satisfy the 3D London equation [3]
Here the integral is along the vortex lines and d3(r) = d(x) d(y) d(z). The resulting magnetic field and energy are, with  mn = [ |rm(z) - rn(z) |2 + 2x2 ]1/2 ,
mn = [ |rm(z) - rn(z) |2 + 2x2 ]1/2 ,
This means all the vortex segments interact with each other similar as magnetic dipoles or tiny current loops, but the magnetic long-range interaction µ 1/r is screened by a factor exp mn /
mn / ) . The 3D interaction between curved vortices is visualized in Fig. 6.
) . The 3D interaction between curved vortices is visualized in Fig. 6.
C. Vortices near a surface
The solutions (6) apply to vortices in the bulk. Near the surface of the superconductor these expressions have to be modified. In simple geometries, e.g. for superconductors with one or two planar surfaces surrounded by vacuum, the magnetic field and energy of a given vortex arrangement is obtained by adding the field of appropriate images (in order to satisfy the boundary condition that no current crosses the surface) and a magnetic stray field which is caused by a fictitious surface layer of magnetic monopoles and which makes the total magnetic field continuous across the surface [9]. The magnetic field and interaction of straight vortices oriented perpendicular to a superconducting film of arbitrary thickness is calculated in Ref. [10,11].
D. Thin Films and Layered Superconductors
Near the surface of a superconductor the self and interaction energies are modified. In films of thickness d 
 the short 2D vortices interact mainly via their magnetic stray field outside the superconductor over an effective penetration depth L = 2
the short 2D vortices interact mainly via their magnetic stray field outside the superconductor over an effective penetration depth L = 2 2 / d. At short distances r
2 / d. At short distances r  L this interaction is logarithmic as in the bulk case, and at large r
L this interaction is logarithmic as in the bulk case, and at large r 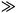 L it decreases as exp(-r / L). With decreasing thickness d, the Fourier transform of the 2D vortex interaction V(r) = ò (d2k / 4p2)
L it decreases as exp(-r / L). With decreasing thickness d, the Fourier transform of the 2D vortex interaction V(r) = ò (d2k / 4p2) 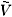 (k) exp(ikr) changes from
(k) exp(ikr) changes from 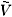 (k) = E0 (k2 + l-2 )-1 (d
(k) = E0 (k2 + l-2 )-1 (d 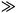
 ) to
) to 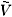 (k) = E0(k2 +kL-1)-1 (d
(k) = E0(k2 +kL-1)-1 (d 
 ) where E0 = d
) where E0 = d  /(m0
/(m0
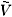 (k) = E0d
(k) = E0d 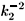 (
( -2 +
-2 +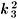 )-1, where now d is the distance between the layers,
)-1, where now d is the distance between the layers, 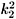 =
= 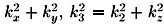 , and
, and  =
=  ab is the penetration depth for currents flowing in these layers [12,3].
ab is the penetration depth for currents flowing in these layers [12,3].
E. Anisotropic Superconductors
For many purposes high-Tc superconductors may be considered as uniaxially anisotropic materials, which within London theory are characterized by two penetration depths  a »
a »  b »
b »  ab (for currents in the ab plane) and
ab (for currents in the ab plane) and  c (for currents along the c axis). The anisotropy ratio G =
c (for currents along the c axis). The anisotropy ratio G =  c /
c /  ab = xab/xc ³ 1 describes also the anisotropy of the GL coherence lengths, xab and xc, which are needed as inner cutoff lengths in the anisotropic London theory. The general solution for arbitrarily arranged straight or curved vortex lines is [3]
ab = xab/xc ³ 1 describes also the anisotropy of the GL coherence lengths, xab and xc, which are needed as inner cutoff lengths in the anisotropic London theory. The general solution for arbitrarily arranged straight or curved vortex lines is [3]
with the tensorial interaction (a, b = x, y, z)
Here g(k,q) =  q2 +
q2 + (k2 -q2) = (L1 k2 + L2 q2)
(k2 -q2) = (L1 k2 + L2 q2)  /
/ enters the cutoff factor exp(-2g); q = k ×
enters the cutoff factor exp(-2g); q = k × ,
,  is the unit vector along the c-axis, L1 =
is the unit vector along the c-axis, L1 =  , L2 =
, L2 =  -
- ³ 0, and the sums and integrals are over the mth and nth vortex line. Due to the tensorial character of fab(r) the contribution of the segment drm to B(r) now in general is not parallel to drm.
³ 0, and the sums and integrals are over the mth and nth vortex line. Due to the tensorial character of fab(r) the contribution of the segment drm to B(r) now in general is not parallel to drm.
III. Ginzburg-Landau, Pippard, and BCS Theories
The London theory was extended in two ways, which both introduce a second length x: The Ginzburg-Landau (GL) theory is nonlinear in y and the Pippard theory is nonlocal in A. All three theories later were shown to follow from the microscopic BCS theory in limiting cases.
A. Ginzburg-Landau Theory
The GL theory of 1950 introduces a complex order parameter y(r) in addition to the magnetic field B(r) = Ñ × A(r). The GL function y(r) is proportional to the BCS energy-gap function D(r), and its square |y(r)|2 to the density of Cooper pairs. The superconducting coherence length x gives the scale over which y(r) can vary, while  governs the variation of the magnetic field as in London theory. Both
governs the variation of the magnetic field as in London theory. Both  and x diverge at the superconducting transition temperature Tc according to
and x diverge at the superconducting transition temperature Tc according to  µ x µ (Tc -T)-1/2, but their ratio, the GL parameter k =
µ x µ (Tc -T)-1/2, but their ratio, the GL parameter k =  /x, is nearly independent of the temperature T. The GL theory reduces to the London theory (which is valid down to T = 0) in the limit x
/x, is nearly independent of the temperature T. The GL theory reduces to the London theory (which is valid down to T = 0) in the limit x 
 , which means constant magnitude |y(r)| = const, except in the vortex cores, where y vanishes. The GL equations are obtained by minimizing a free energy functional F{ y, A } with respect to the GL function y(r) and the vector potential A(r). With the length unit
, which means constant magnitude |y(r)| = const, except in the vortex cores, where y vanishes. The GL equations are obtained by minimizing a free energy functional F{ y, A } with respect to the GL function y(r) and the vector potential A(r). With the length unit  and magnetic field unit
and magnetic field unit  Bc the GL functional reads
Bc the GL functional reads
This functional and the resulting GL equations may be expressed in terms of the real function |y| and the gauge-invariant supervelocity Ñj/k- A where j(r) is the phase of y = |y| exp(ij). The supercurrent density is J = 
 2(Ñj/k-A) |y|2. In an external field Ha one has to minimize not the free energy F but the Gibbs free energy G = F -
2(Ñj/k-A) |y|2. In an external field Ha one has to minimize not the free energy F but the Gibbs free energy G = F -  Ha. The condition ¶G/¶
Ha. The condition ¶G/¶ yields the equilibrium field Ha = ¶F /¶
yields the equilibrium field Ha = ¶F /¶ . The reversible magnetization curves
. The reversible magnetization curves  (Ha) of pin-free superconductors, Fig. 5, were calculated in this way from GL theory [8], together with the profiles of Fig. 3.
(Ha) of pin-free superconductors, Fig. 5, were calculated in this way from GL theory [8], together with the profiles of Fig. 3.
The GL theory modifies the London interaction between vortices in two ways: (a) The range of the magnetic repulsion at large inductions  becomes larger,
becomes larger,  ¢ =
¢ =  /(1-
/(1- /Bc2)1/2. (b) A weak attraction of range x¢ = x/(2-2
/Bc2)1/2. (b) A weak attraction of range x¢ = x/(2-2 /Bc2)1/2 is added, caused by the condensation energy that is gained by the overlap of the vortex cores. Parallel vortex lines then interact by an effective potential V(r) µ K0(r/
/Bc2)1/2 is added, caused by the condensation energy that is gained by the overlap of the vortex cores. Parallel vortex lines then interact by an effective potential V(r) µ K0(r/ ¢) - K0(r/x¢) which no longer diverges at zero distance r [13].
¢) - K0(r/x¢) which no longer diverges at zero distance r [13].
B. Pippard Theory
Inspired by Chamber's nonlocal generalization of Ohm's law, Pippard 1953 introduced a superconductor coherence length x by generalizing the London equation m0J = - A to a nonlocal relationship [2]
A to a nonlocal relationship [2]
In the presence of electron scattering with mean free path l, the Pippard penetration depth  P = (
P = ( x0/x)1/2 exceeds the London penetration depth
x0/x)1/2 exceeds the London penetration depth  L of a pure material with coherence length x0, since the effective coherence length x is reduced by scattering, x-1 »
L of a pure material with coherence length x0, since the effective coherence length x is reduced by scattering, x-1 »  + l-1 [2]. In the limit of small x
+ l-1 [2]. In the limit of small x 
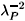 A(r). In Fourier space Pippard's Eq. (10) reads m0J(k) = - QP(k)A(k) with
A(r). In Fourier space Pippard's Eq. (10) reads m0J(k) = - QP(k)A(k) with
This Pippard theory is useful mainly for superconductors with small GL parameter k.
BCS Theory
The microscopic BCS theory (in the Green function formulation of Gor'kov) for weak magnetic fields yields a similar nonlocal relation m0J(k) = -Q(k)A(k) as suggested by Pippard, replacing the Pippard kernel QP(k) by the BCS kernel [14,3]
Here h(x) is defined in Eq. (11),  (T) = QBCS(0)-1/2 »
(T) = QBCS(0)-1/2 »  (0) (1 - T4/
(0) (1 - T4/ )-1/2 is the temperature dependent magnetic penetration depth, and xK =
)-1/2 is the temperature dependent magnetic penetration depth, and xK =  vF /(2pkBT) » 0.844
vF /(2pkBT) » 0.844  (T) Tc / (kT) (vF = Fermi velocity, k = GL parameter). The range of the BCS Gorkov kernel is of the order of the BCS coherence length x0 =
(T) Tc / (kT) (vF = Fermi velocity, k = GL parameter). The range of the BCS Gorkov kernel is of the order of the BCS coherence length x0 =  vF / (pD0) where D0 is the BCS energy gap at T = 0.
vF / (pD0) where D0 is the BCS energy gap at T = 0.
With the nonlocal relation m0J(k) = -Q(k)A(k) the Eq. (2) for a vortex line at rn = 0 now becomes [ 1 + Q(k)-1 k2 ]  (k) = F0 with the solution
(k) = F0 with the solution
where J0(x) is a Bessel function. The Pippard or BCS field B(r) (13) of an isolated vortex line is no longer monotonic as compared with the London field, cf. Eq. (3), but it exhibits a field reversal with a negative minimum at large distances r
P from the vortex core. This effect should be observable if x », i.e., for clean superconductors with small GL parameter k at low temperatures. See also recent work on this nonlocal electrodynamics [15].
», i.e., for clean superconductors with small GL parameter k at low temperatures. See also recent work on this nonlocal electrodynamics [15].
The field reversal of the vortex field is partly responsible for the attractive interaction between flux lines at large distances, which was observed in clean Niobium at temperatures not too close to Tc and which follows from BCS theory at T < Tc for pure superconductors with GL parameter k close to 1/  . This attraction leads to abrupt jumps in the magnetization curve and to an agglomeration of flux lines that can be observed in superconductors with demagnetization factor N ¹ 0 as FLL islands surrounded by Meissner state, or Meissner islands surrounded by FLL [16]. For the definition of N see Sec. 5.
. This attraction leads to abrupt jumps in the magnetization curve and to an agglomeration of flux lines that can be observed in superconductors with demagnetization factor N ¹ 0 as FLL islands surrounded by Meissner state, or Meissner islands surrounded by FLL [16]. For the definition of N see Sec. 5.
Another BCS effect which differs from the GL result is that in clean superconductors at low temperatures the periodic magnetic field B(x,y) of the FLL near Bc2 is not a smooth spatial function as in GL theory, but has sharp conical maxima and minima such that the profile B(x,0) along a nearest neighbor direction has zig-zag shape [3]. The reason for this is that the electron mean free path in pure superconductors at T ® 0 becomes larger than the vortex spacing a0. This leads to a slow decrease of the Fourier coefficients BK µ (-1)m+mn+n of B(x,y), while at T » Tc the GL theory near Bc2 yields a rapid decrease, BK µ (-1)m+mn+n exp(-
of B(x,y), while at T » Tc the GL theory near Bc2 yields a rapid decrease, BK µ (-1)m+mn+n exp(- x1 y2/8p). Here K = Kmn = (2p/x1 y2)(my2; -mx2+nx1) (m,n = 1,2,3, ...) are the reciprocal lattice vectors of the ideal vortex lattice with positions Rmn = (mx1+nx2;ny2), and x1 y2 = F0 /
x1 y2/8p). Here K = Kmn = (2p/x1 y2)(my2; -mx2+nx1) (m,n = 1,2,3, ...) are the reciprocal lattice vectors of the ideal vortex lattice with positions Rmn = (mx1+nx2;ny2), and x1 y2 = F0 /  is the area of the unit cell, see Fig. 2.
is the area of the unit cell, see Fig. 2.
IV. Elasticity of the Vortex Lattice
The flux-line displacements caused by pinning forces and by thermal fluctuations may be calculated using the elasticity theory of the FLL. Fig. 7 visualizes the three basic distortions of the triangular FLL: shear, uniaxial compression, and tilt. The linear elastic energy Felast of the FLL is obtained by expanding its free energy F with respect to small displacements un (z) = rn(z) -Rn = (unx,uny) of the flux lines from their ideal parallel lattice positions Rn and keeping only the quadratic terms. This yields [3]
where u(k) is the Fourier transform of the displacement field un(z), now (a,b) = (x,y), and k = (kx,ky,kz). The k-integral in Eq. (14) is over the first Brillouin zone (BZ) of the FLL since the "elastic matrix'' Fab(k) is periodic in the kx,ky plane; the finite vortex core radius restricts the kz integration to |kz| £ x-1. For an elastic medium with uniaxial symmetry the elastic matrix reads
The coefficients c11, c66, and c44 are the elastic moduli of uniaxial compression, shear, and tilt, respectively. For the FLL, Fab(k) was calculated from GL and London theories [3]. The result, a sum over reciprocal lattice vectors, should coincide with expression (15) in the continuum limit, i.e., for small |k|  kBZ, where kBZ = (4p
kBZ, where kBZ = (4p /F0)1/2 is the radius of the circularized (actually hexagonal) Brillouin zone of the triangular FLL with area p
/F0)1/2 is the radius of the circularized (actually hexagonal) Brillouin zone of the triangular FLL with area p  Z. In the London limit one finds for isotropic superconductors the elastic moduli
Z. In the London limit one finds for isotropic superconductors the elastic moduli
The GL theory yields an additional factor (1- /Bc2)2 in c66, i.e., c66 µ
/Bc2)2 in c66, i.e., c66 µ  (
( -Bc2)2, and replaces
-Bc2)2, and replaces  in c11(k) by
in c11(k) by  ¢ [17,8]. The k dependence (dispersion) of the compression and tilt moduli c11(k) and c44(k) means that the elasticity of the vortex lattice is nonlocal, i.e., strains with short wavelengths 2p/k
¢ [17,8]. The k dependence (dispersion) of the compression and tilt moduli c11(k) and c44(k) means that the elasticity of the vortex lattice is nonlocal, i.e., strains with short wavelengths 2p/k  2p
2p have a much lower elastic energy than a homogeneous compression or tilt (corresponding to k ® 0). This elastic nonlocality comes from the fact that the magnetic interaction between the flux lines typically has a range
have a much lower elastic energy than a homogeneous compression or tilt (corresponding to k ® 0). This elastic nonlocality comes from the fact that the magnetic interaction between the flux lines typically has a range  much longer than the flux-line spacing a0, therefore, each flux line interacts with many other flux lines. Note that large
much longer than the flux-line spacing a0, therefore, each flux line interacts with many other flux lines. Note that large  causes a small shear stiffness since c66 µ
causes a small shear stiffness since c66 µ  -2, Eq. (16), and a smaller c11(k >
-2, Eq. (16), and a smaller c11(k >  -1), but the uniform compressibility c11(k = 0) is independent of
-1), but the uniform compressibility c11(k = 0) is independent of  .
.
The compressional modulus c11 and the typically much smaller shear modulus c66
c11 » c44 originate from the flux-line interaction, but the last term in the tilt modulus c44 (16) originates from the line tension of isolated flux lines, defined by P = lim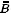 ® 0 (c44 F0/
® 0 (c44 F0/ ). In isotropic (or cubic) superconductors like Nb and its alloys, the line tension P coincides with the self energy Fs of a flux line, P = Fs, Fs = F0 Hc1 » (
). In isotropic (or cubic) superconductors like Nb and its alloys, the line tension P coincides with the self energy Fs of a flux line, P = Fs, Fs = F0 Hc1 » (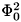 /4pm02) (ln k+0.5) for k
/4pm02) (ln k+0.5) for k 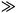 1. In anisotropic materials the line tension and line energy of flux lines in general are different and depend on the angle q of the vortex line with respect to the c-axis. One has P(q) = Fs(q)+¶2 Fs/¶q2. Using Fs(q) = Fs(0) (cos2q+ G-2 sin2q)1/2 with G =
1. In anisotropic materials the line tension and line energy of flux lines in general are different and depend on the angle q of the vortex line with respect to the c-axis. One has P(q) = Fs(q)+¶2 Fs/¶q2. Using Fs(q) = Fs(0) (cos2q+ G-2 sin2q)1/2 with G =  c /
c / ab ³ 1, one obtains P(0) = Fs(0) /G2 and P(p/2) = Fs(p/2) G2 = P(0) /G3 (for tilt out of the ab-plane) [3]. In isotropic superconductors the uniaxial symmetry of the ideal vortex lattice, i.e., the appearance of a preferred axis, is induced by the applied magnetic field. This induced anisotropy leads to a small difference between the compressional and tilt moduli c11 and c44, but not to a difference between line energy and line tension.
ab ³ 1, one obtains P(0) = Fs(0) /G2 and P(p/2) = Fs(p/2) G2 = P(0) /G3 (for tilt out of the ab-plane) [3]. In isotropic superconductors the uniaxial symmetry of the ideal vortex lattice, i.e., the appearance of a preferred axis, is induced by the applied magnetic field. This induced anisotropy leads to a small difference between the compressional and tilt moduli c11 and c44, but not to a difference between line energy and line tension.
As a consequence of nonlocal elasticity, the flux-line displacements un(z) caused by local pinning forces, and also the space and time averaged thermal fluctuations áun(z)2ñ, are much larger than they would be if c44(k) had no dispersion, i.e., if it were replaced by c44(0) =  Ha »
Ha »  2/m0. The maximum vortex displacement u(0) µ f caused at r = 0 by a point force of density f d3(r), and the thermal fluctuations áu2 ñ µ kB T, are given by similar expressions [3],
2/m0. The maximum vortex displacement u(0) µ f caused at r = 0 by a point force of density f d3(r), and the thermal fluctuations áu2 ñ µ kB T, are given by similar expressions [3],
In this result a large factor [c44(0) / c44(kBZ) ]1/2 » kBZ » p
» p /a
/a 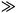 1 originates from the elastic nonlocality. In anisotropic superconductors with B||c, the thermal fluctuations (17) are enhanced by an additional factor G =
1 originates from the elastic nonlocality. In anisotropic superconductors with B||c, the thermal fluctuations (17) are enhanced by an additional factor G =  c/
c/ ab [3]. For an exact analytic evaluation of the integral (17) for áu2ñ see [18].
ab [3]. For an exact analytic evaluation of the integral (17) for áu2ñ see [18].
V. High-Tc Superconductors
The nonlocal elastic response of the vortex lattice is particularly important for understanding the thermodynamic and electrodynamic properties of the high-Tc superconductors, which were discovered in 1987 and the following years. These oxides with high superconducting transition temperature Tc (e.g. YBa2Cu3O7-d with Tc = 92.5 K, Bi2Sr2Ca2Cu3O10+d with Tc = 120 K, and some Hg and Tl compounds with even higher Tc) are layered structures with more or less decoupled superconducting Cu-O layers. They thus exhibit high anisotropy of their superconducting properties. For example, YBCO has an anisotropy G = 5 and BSCCO has G » 100. This means in BSCCO the layers are almost decoupled and the penetration depth  c for currents flowing along the c axis is macroscopically large,
c for currents flowing along the c axis is macroscopically large,  c = G
c = G ac with
ac with  ab » 140 nm at T = 0. Therefore, the magnetic field component parallel to the layers penetrates easily.
ab » 140 nm at T = 0. Therefore, the magnetic field component parallel to the layers penetrates easily.
This large
c also causes very pronounced elastic nonlocality, which means a very soft vortex lattice. The vortices are thus strongly pinned collectively, since the vortex lattice adjusts to the pins, but at higher temperatures they are easily depinned by thermal activation, since the elementary pinning energy of very flexible vortices is small. By the same token, thermal fluctuations of the vortices are large and may even cause melting of the vortex lattice into a vortex liquid. The effects of the elastic nonlocality and anisotropy on the thermal fluctuation, melting, and pinning of the FLL are treated in detail in the review [19], where also phase diagrams in the Ha-T plane are presented for 3D and layered superconductors. Phase diagrams obtained by applying simple Lindemann criteria (áu2ñ = 
 , cL» 0.25) to both thermal and pinning-caused fluctuations in 3D superconductors at not too low fields (
, cL» 0.25) to both thermal and pinning-caused fluctuations in 3D superconductors at not too low fields ( > Bc1) are calculated in [20], namely, the line Hm(T) where the FLL melts, the line Hsv(T) which separates the regimes of single-vortex-pinning and of vortex-bundle-pinning, and the order-disorder line Hdis(T) above which pinning causes plastic deformation of the FLL, see Fig. 8. In this case (B = m0H, no decoupling of layers) the phase diagram in reduced units Ha/Hc2(0) and t = T/Tc, depends only on the Ginzburg number Gi and on the pinning strength D = [ Jc(0)/J0(0) ]1/2 (critical current for B® 0 over the depairing current, both at T = 0), see [20].
> Bc1) are calculated in [20], namely, the line Hm(T) where the FLL melts, the line Hsv(T) which separates the regimes of single-vortex-pinning and of vortex-bundle-pinning, and the order-disorder line Hdis(T) above which pinning causes plastic deformation of the FLL, see Fig. 8. In this case (B = m0H, no decoupling of layers) the phase diagram in reduced units Ha/Hc2(0) and t = T/Tc, depends only on the Ginzburg number Gi and on the pinning strength D = [ Jc(0)/J0(0) ]1/2 (critical current for B® 0 over the depairing current, both at T = 0), see [20].
VI. Continuum Description of the Vortex State
If one is interested only in length scales larger than the vortex spacing a0, one may use a continuum description of the vortex state to calculate the distributions of magnetic field and current in superconductors of arbitrary shape. Two different algorithms where presented [21,22] which in principle allow to compute the electromagnetic behavior of superconductors of arbitrary shape with and without vortex pinning. The extension to finite London depth  is given in [5].
is given in [5].
Apart from the Maxwell equations, a continuum description requires the constitutive laws of the superconductor. These may be obtained, e.g., from the London theory, Sct. II, by taking the limits a0 ® 0 and l® 0 (or keeping finite  [5]), and from appropriate models of vortex dynamics. One constitutive law is the reversible magnetization curve of a pin-free superconductor, M (H) or
[5]), and from appropriate models of vortex dynamics. One constitutive law is the reversible magnetization curve of a pin-free superconductor, M (H) or  (H) = m0 H + m0M(H), where H is an effective applied field which would be in equilibrium with the local induction
(H) = m0 H + m0M(H), where H is an effective applied field which would be in equilibrium with the local induction  . In the simplest case this law may read M = 0 or
. In the simplest case this law may read M = 0 or  = m0H, valid if everywhere
= m0H, valid if everywhere  is larger than several times the lower critical field Bc1. But in general the reversible M(H) computed from London or GL theories should be used, as discussed in [21,22,23,24].
is larger than several times the lower critical field Bc1. But in general the reversible M(H) computed from London or GL theories should be used, as discussed in [21,22,23,24].
When the finite lower critical field Hc1 is accounted for, the magnetization curve M(Ha) in general is irreversible (i.e. a loop) even in complete absence of vortex pinning. This pin-free irreversibility is caused by a geometric barrier for the penetration of magnetic flux, which is absent only if the superconductor has the shape of an ellipsoid or if it has a sharp edge or cusp, at which the applied field Ha is strongly enhanced such that flux lines can penetrate easily. For example, in superconducting cylinders or strips with rectangular cross section 2a ×2b (2a = diameter or width, 2b = height) in increasing Ha, the magnetic flux penetrates first reversibly at the four corners in form of nearly straight flux lines, see Figs. 4, 9 . When the field of first flux entry Ben is reached, these flux lines join at the equator, contract, and jump to the specimen center, from where they gradually fill the entire superconductor. When Ha is decreased again, some flux exits first reversibly, but below a reversibility field Hrev > Hen the magnetization loop opens, see Fig. 10, since the barrier for flux exit is absent or weaker than the barrier for flux entry. For arbitrary aspect ratio b/a the entry field is [22,24]
where c = 0.36 for strips and c = 0.67 for disks or cylinders. This geometric barrier should not be confused with the Bean-Livingstone barrier for the penetration of a straight vortex line into the planar surface of a superconductor, which would lead to a similar asymmetric magnetization loop. The geometric barrier is caused by the line tension of the vortices penetrating at sharp [21,22,24] or rounded [25] corners. This line tension P (see Sct. IV) is balanced by the Lorentz force exerted on the vortex ends by the surface screening currents and directed towards the specimen center. The irreversible magnetic behavior of thin strips with an edge barrier (and without or with bulk pinning) in perpendicular Ha was calculated analytically by Zeldov et al. [26].
The computed irreversible magnetization loops of pin-free superconductor cylinders with various aspect ratios b/a = 0.08 (thin disk) to b/a = ¥ (long cylinder) in an axial field Ha are depicted in Fig. 10 , together with the corresponding reversible magnetization curves of ellipsoids which have the same initial slope (Meissner state) as the cylinders. These magnetization loops of cylinders (like those of other non-ellipsoids) have a maximum at Ha » Hen, and at Ha > Hrev they are reversible and coincide with the magnetization of the corresponding ellipsoid. All pin-free magnetization loops are symmetric, M(-Ha) = -M(Ha) with M(0) = 0, i.e., no remanent flux can remain at Ha = 0 since bulk pinning is absent and there is no barrier for flux exit when Ha = 0. Fig. 11 shows magnetization curves of a short cylinder with finite Hc1 for various strengths of bulk pinning.
The reversible magnetization curves of pin-free ellipsoids M(Ha,N) follow from the magnetization curve M(Ha,N = 0) =  /m0 -Ha of long cylinders in parallel field Ha by the concept of a demagnetization factor N. One has 0 £ N £ 1, N = 0 for parallel geometry, N = 1/2 for infinite cylinders in perpendicular field, N = 1/3 for spheres, and N = 1 for thin films in perpendicular field. For ellipsoids with N ¹ 0 one has to solve the implicit equation for an effective internal field Hi [24],
/m0 -Ha of long cylinders in parallel field Ha by the concept of a demagnetization factor N. One has 0 £ N £ 1, N = 0 for parallel geometry, N = 1/2 for infinite cylinders in perpendicular field, N = 1/3 for spheres, and N = 1 for thin films in perpendicular field. For ellipsoids with N ¹ 0 one has to solve the implicit equation for an effective internal field Hi [24],
to obtain the reversible magnetization M(Ha, N) = M(Hi, N = 0) (dashed lines in Fig. 10) from the M(Ha, N = 0) of longitudinal geometry. In particular, in the Meissner state ( º 0) one has M(Ha, 0) = -Ha and M(Ha, N) = -Hi = -Ha /(1-N) for |Ha| £ (1-N)Hc1.
º 0) one has M(Ha, 0) = -Ha and M(Ha, N) = -Hi = -Ha /(1-N) for |Ha| £ (1-N)Hc1.
As a second constitutive law one may use the local electric field E = Ev(J,B) which is generated by moving vortices and which in a compact way can describe free flux flow and Hall effect, but also vortex pinning and thermally activated depinning or creep. A simple but still quite general isotropic model is Ev = r(J,B) J with r = const·B ·(J/Jc)n-1, where Jc is the critical current density and n the creep exponent [5,27]. This realistic model means an activation energy U(J) = U0 ln(Jc /J) for depinning that enters in E = Ec exp[ -U(J) /kT ] = Ec (J/Jc)n with n = U0 /kT. Within this model, flux flow is described by n = 1, flux creep (relaxation with approximately logarithmic time law) by n 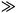 1, and Bean's critical state model of vortex pinning by the limit n ® ¥. In general, both Jc and n may depend on the local induction
1, and Bean's critical state model of vortex pinning by the limit n ® ¥. In general, both Jc and n may depend on the local induction  and on the temperature T. Fig. 12 shows some magnetization loops of a short cylinder calculated in [27] for two different Jc(B) models and two creep exponents. For the electrodynamics of thin strips, disks, and rings in a perpendicular field see [28,29,30], and for thin rectangles and films of other shapes see [31,32]. Thin strips in perpendicular dc and ac magnetic fields and with transport current are considered in [33]. Analytic and numerical solutions were also obtained for flux expulsion and penetration into thin strips with a bend along the middle line [34] and for thin shells (or hats) of conical shape [35].
and on the temperature T. Fig. 12 shows some magnetization loops of a short cylinder calculated in [27] for two different Jc(B) models and two creep exponents. For the electrodynamics of thin strips, disks, and rings in a perpendicular field see [28,29,30], and for thin rectangles and films of other shapes see [31,32]. Thin strips in perpendicular dc and ac magnetic fields and with transport current are considered in [33]. Analytic and numerical solutions were also obtained for flux expulsion and penetration into thin strips with a bend along the middle line [34] and for thin shells (or hats) of conical shape [35].
In all these calculations the London depth  was assumed to be negligibly small. Finite l may be accounted for by modifying the current-voltage law, using E = Ev(J,B) + m0
was assumed to be negligibly small. Finite l may be accounted for by modifying the current-voltage law, using E = Ev(J,B) + m0
- 1. P.G. DeGennes, Superconductivity of Metals and Alloys, New York, Benjamin, 1966.
- 2. M. Tinkham, Introduction to Superconductivity, New York, McGraw-Hill, 1975.
- 3. E.H. Brandt, Rep. Progr. Phys. 58 (1995) 1465-1594.
- 4. E.H. Brandt and G.P. Mikitik, Phys. Rev. Lett. 85 (2000) 4164.
- 5. E.H. Brandt, Phys. Rev. B 64 (2001) 024505, 1-15.
- 6. J.R. Clem, J. Low Temp. Phys. 18 (1975) 427.
- 7. Z. Hao, J.R. Clem, M.W. Mc Elfresh, L. Civale, A.P. Malozemov, F. Holtzberg, Phys. Rev. B 43 (1991) 2844.
- 8. E.H. Brandt, Phys. Rev. Lett. 78 (1997) 2208.
- 9. E.H. Brandt, J. Low Temp. Phys. 42 (1981) 557.
- 10. Jung-Chun Wei, Tzong-Yer Yang, Jpn. J. Appl. Phys. 35 (1996) 5696.
- 11. G. Carneiro, E.H. Brandt, Phys. Rev. B 61 (2000) 6370.
- 12. J.R. Clem, Phys. Rev. B 43 (1991) 7837.
- 13. E.H. Brandt, Phys. Rev. B 34 (1986) 6514.
- 14. A.A. Abrikosov, L.P. Gorkov, I.E. Dzyaloshinski, Methods of Quantum Field Theory in Statistical Physics, Englewood Cliffs, Prentice Hall, 1963.
- 15. V.G. Kogan et al., Phys. Rev. B 54 (1996) 12386.
- 16. E.H. Brandt, U. Essmann, phys. stat. sol. (b) 144 (1987) 13.
- 17. E.H. Brandt, Phys. Stat. Sol. b, 77 (1976) 709.
- 18. I.M. Babich, Yu.V. Sharlai, G.P. Mikitik, Fiz. Nizk. Temp. 20 (1994) 227 [Low Temp. Phys. 20 (1994) 220].
- 19. G. Blatter, M.V. Feigel'man, V.B. Geshkenbein, A.I. Larkin, V.M. Vinokur, Rev. Mod. Phys. 66 (1994) 1125.
- 20. G.P. Mikitik, E.H. Brandt, Phys. Rev. B 64 184514 (2001), 1-14.
- 21. R. Labusch, T.B. Doyle, Physica C 290 (1997) 143.
- 22. E.H. Brandt, Phys. Rev. B 59 (1999) 3369.
- 23. T. Hocquet, P. Mathieu and Y. Simon, Phys. Rev. B 46 (1992) 1061.
- 24. E.H. Brandt, Phys. Rev. B 60 (1999) 11939.
- 25. M. Benkraouda, J.R. Clem, Phys. Rev. B 58 (1998) 15103.
- 26. E. Zeldov, A.I. Larkin, V.B. Geshkenbein, M. Konczykowski, D. Majer, B. Khaykovich, V.M. Vinokur, H. Strikhman, Phys. Rev. Lett. 73 (1994) 1428.
- 27.E.H. Brandt, Phys. Rev. B 58 (1998) 6506.
- 28. E.H. Brandt, Phys. Rev. B 50 (1994) 4034.
- 29. D.V. Shantsev, Y.M. Galperin, T.H. Johansen, Phys. Rev. B 60 (1999) 13112.
- 30. E.H. Brandt, Phys. Rev. B 55 (1997) 14513.
- 31. L. Prigozhin, J. Comput. Phys. 144 (1998) 180.
- 32. E.H. Brandt, Phys. Rev. B 52 (1995) 15442.
- 33. G.M. Mikitik and E.H. Brandt, Phys. Rev. B 64 (2001) 092502, 1-4.
- 34. Leonardo R.E. Cabral and J. Albino Aguilar, Physica C 341-348, 1049 (2000).
- 35. Leonardo R.E. Cabral, Thesis, Universidade Federal de Pernambuco, Recife (2001).
Publication Dates
-
Publication in this collection
04 Dec 2002 -
Date of issue
Sept 2002
History
-
Received
28 Feb 2002
































