Static magneto optical birefringence of new Electric Double Layered Magnetic Fluids

Static magneto optical birefringence of new Electric Double Layered Magnetic Fluids

J. Depeyrot1^*, G. J. da Silva¹, C. R. Alves¹, E. C. Sousa¹, M. Magalhães²,

A. M. Figueiredo Neto², M. H. Sousa³, and F. A. Tourinho³

¹ Complex Fluids Group, Instituto de Física,

Universidade de Brasília, Caixa Postal 04455, 70919-970, Brasília (DF), Brazil

² Instituto de Física, Universidade de São Paulo,

Caixa Postal 66318, São Paulo (SP), Brazil

³ Complex Fluids Group, Instituto de Química,

Universidade de Brasília, Caixa Postal 04478, 70919-970 Brasília (DF), Brazil

Received on 27 May, 2001

Magnetic birefringence measurements are performed under a static field on Electric Double Layered Magnetic Fluids based on copper and zinc ferrite nanostructures. The optical birefringence is related to a single-particle effect and well described by a Langevin model which includes a log- normal distribution of particles. By the field-induced birefringence level, these new magnetic fluids are comparable to usual ones, a result which could offer a new way for biological applications.

I Introduction

Nowadays, Magnetic Fluids (MF) or Ferrofluids are stable colloidal suspensions of magnetic monodomain nanosized particles dispersed in a specific liquid carrier [1]. Due in part to the coexistence of a strong magnetization with fluidity properties and also to the versatility of molecular liquids carrier which can be employed, such artificial systems leads to numerous technological applications [2]. Fundamental studies are generally performed in electric double layered magnetic fluids (EDL-MF) [3] where the stabilization is achieved by introducing, between particles, electrostatic repulsive forces obtained by an adjustable surface charge density.

MF have long been investigated using magneto-optical birefringence measurements. For instance, magnetic colloidal sols based on Fe₃O₄ [4], g-Fe₂O₃ [5], CoFe₂O₄ [6] and NiFe₂O₄ [7] nanoparticles are optically active and exhibit strong optical birefringence under magnetic fields. In diluted solutions (typically of the order of 10¹⁶ particles per cm³), the magneto-optical behavior of MF can be well described by a Langevin formalism that includes a log-normal size distribution of roughly spherical particles [4, 8].

Nevertheless, until now, the origin of the MF magneto-optical birefringence is not well understood. A possible field-induced effect on the particle material, the cubic (spinel) crystal structure and the nearly spherical particle shape observed by electron microscopy do not explain the optical anisotropy. Optical birefringence and dichroism of surfacted MF have been interpreted in terms of orientation or aggregation in the presence of a magnetic field of particle aggregates already present in the solution in the absence of the field [9]. However, in EDL-MF, recent Small Angle X-ray scattering measurements performed on a large number of samples show at zero field a low degree of particle aggregation [10]. Formation of chain-like aggregates in the applied field has also been proposed to account for the magneto-optical behavior of MF [11]. Nevertheless, such model results in considerable deviation from experiments at low field. Furthermore, a field induced aggregation of particles in EDL-MF is rejected by Small Angle Neutron Scattering results if the ionic strength of the solutions is less than 0.05 mol L^-1 with particles of surface charge density about 0.2 C m^-2 [12].

More recently, static magneto-optical birefringence of size sorted g-Fe₂O₃ nanoparticles indicated [13], on the contrary, that the optical anisotropy observed in EDL-MF is not due to cooperative process of particle agglomeration in the field but to a particle surface magnetic anisotropy, coming from the discontinuity of magnetic interactions between individual spins which reside at the particle surface, coupled to a slight ellipticity of the particles.

The aim of the present work is to investigate the static magneto-optical birefringence of new EDL-MF based on copper and zinc ferrite nanoparticles. The chemical synthesis of these ferrofluids as well as their magnetic properties have already been presented in a previous paper [14]. Such MF could offer a new alternative for biological applications since their iron content is reduced and they would therefore be notably easier to titrate in biological in vivo experiments. In such a context, it is essential to check their optical birefringence level since optical birefringence measurements have shown to be a useful tool in testing the grafting of magnetic nanoparticles by antibodies [15].

The current work is divided as follows. In section II, we give a brief description of the EDL-MF chemical synthesis as well as a chemical and structural analysis of the synthesized nanoparticles. Parts of our previous magnetization data obtained at 300 K are reviewed in section III. Then, in section IV, static magneto-optical measurements are presented and discussed within the framework of the Langevin model.

II Chemical synthesis and particle characterization

EDL-MF synthesis. The EDL-MF elaboration is carried out on three basic steps [14]: firstly, the ferrite nanoparticles synthesis, then the chemical surface treatment, and finally the peptization of the particles in a stable aqueous colloidal solution. CuFe₂O₄ and ZnFe₂O₄ oxide nanoparticles were prepared using hydrothermal coprecipitating aqueous solution of CuCl₂-FeCl₃ and ZnCl₂-FeCl₃ mixtures, respectively, in alkaline medium. After the coprecipitation step, the precipitate is washed in order to suppress the high ionic strength of the medium and the particle surface is cleaned by a (2 mol L^-1) HNO₃ solution. Moreover, to ensure the thermodynamical stability of the particles an empirical process has been proposed: the precipitated is boiled with a 0.5 mol L^-1 Fe(NO₃)₃ solution. Then, the particles are conveniently peptized in acid medium by the adjustment of the ionic strength, resulting in a stable sol of high quality.

Chemical analysis. Once the EDL-MF synthesis has been performed, the sample composition is controlled by chemical analysis: iron(III) titration is determined by dichromatometry. Copper (II) titration is done by volumetric analysis with iodine and zinc (II) is quantified using plasma emission spectroscopy. Then, each MF precursor solution is diluted at two volume fraction of magnetic nanomaterial, F = 0.73% and F = 0.15% for Cu-based samples and F = 0.75% and F = 0.16% for Zn-based ones. These volume fraction values have been chosen in order to perform magnetization and magneto-optical measurements on sufficiently dilute samples where the inter-particles interactions can be considered as negligible and the independent particle model well works.

Magnetic material yield. The experimental procedure used to determine the best value in divalent metal molar fraction is an adaptation of the method of continuous variation or "Job's method". A series of solutions of equal total concentration in metal [M²⁺ + Fe³⁺] is prepared with different relative amounts of M²⁺ and Fe³⁺ reacting in excess of sodium hydroxide in order to obtain the ferrite nanoparticles. For each solution, the corresponding magnetic material yield is measured using an adaptation of the Gouy method, where an apparent increase in mass Dm can be detected when the solution is submitted to a magnetic field gradient. Fig. 1 displays the variations of the normalized value of the magnetic material yield as a function of the divalent metal molar fraction X_M²⁺. As it can be seen, our measurements show a very good agreement with the theoretical curve deduced from the chemical reaction of ferrite formation [14]. The maximum yield corresponds to that provided by the exact ferrite stoichiometry with a value of X_M²⁺ equal to 0.33.

Figure 1.
X-ray powder difratograms of copper and zinc ferrite nanoparticles. The characteristic diffracted directions [220], [311], [400], [422], [511], [440] and [533] of the spinel structure are indexed.

X-rays diffraction. In order to characterize the crystalline structure of our magnetic nanoparticles, X-rays diffraction measurements were performed on powder samples obtained after evaporation of the liquid carrier, using a Rigaku/Denki X-rays diffractometer and the CuKa radiation at 1.54 Å. We present in Fig. 2 a typical powder diffraction pattern which exhibits several lines corresponding to the characteristic interplanar spacing [220], [311], [400], [422], [511], [440] and [533] of the spinel structure [16]. Table 1 compares for both kind of nanomaterial the measured peak intensities with the American Society for Testing and Materials (ASTM) values [17] and also gives the cubic lattice cell deduced from the peak position with average values of 0.828 nm and 0.832 nm to be compared to the ASTM ones 0.835 nm and 0.844 nm for CuFe₂O₄ and ZnFe₂O₄ respectively.

Figure 2.
Normalized mass variation Dm/Dm_max or magnetic material yield as a function of the divalent metal molar ratio, X_M²⁺.

Table 1:
Crystallographic analysis of Fig. 1 for CuFe₂O₄ and ZnFe₂O₄ nanoparticles. The interplanar spacing d_hkl is calculated from the line position by using the Bragg law and the corresponding cubic lattice cell a is deduced. The experimental peak intensities I_exp are compared to the ASTM ones.

Moreover, the observed line width arises from the finite dimension of the crystal (polycrystalline specimens) and is related to the roughly spherical particle diameter. Additional sources of broadening, arising from the experimental setup and instrumentation, were discounted here using a Si standard monocrystal. Then, using the Scherrer equation [18] it yields a mean diameter d_XR = 8.4 nm in the case of Cu-based nanoparticles and d_XR = 6.3 nm in the case of Zn-based ones.

III Magnetization results

Magnetic properties of Magnetic Fluids arise from the dispersion of magnetic nanoparticles in a liquid carrier. In spinel-type nanoparticles, the exchange interactions between ions of the tetrahedral and the octahedral sites lead to a global ferrimagnetic order in the particles core and due to their small size, each magnetic particles behaves as a single magnetic domain of volume V bearing a permanent magnetic moment m of modulus m_SV, m_S being the nanomaterial magnetization. Then, at 300 K and for enough dilute solutions (for a volume fraction F < 2 %), the magnetic fluid response to an applied field H results from the progressive orientation in the field of an ensemble of non interacting magnetic moment which are free to rotate in the solvent. This superparamagnetic behavior is well described by a Langevin formalism including a log normal size distribution to take into account the size polydispersion of particles [19, 20]. Thus, at T = 300 K and at zero field the magnetization is zero due to thermal fluctuations; as the magnetic field increases, the solution magnetization increases too and does not present any hysteresis. In the limit of small fields, the magnetization is proportional to H and at large magnetic fields, all the magnetic moment are aligned in the field direction and the magnetization saturates scaling a linear law as a function of 1/H. Such a model well works at room temperature for magnetic fluids based on 10 nm sized g-Fe₂O₃ particles, using a nanomaterial magnetization about 75% of the bulk one. Nevertheless, as the proportion of spins located in the neighborhood of the particle surface increases when the particle size is reduced, the magnetic properties of very small particles (typically inferior to 5 nm) is strongly influenced by the spin arrangement of the particle surface. The lower coordination of surface ions does modify the exchange interactions and it has been shown the existence of a superficial shell where the spin configuration can be disordered resulting then in a reduced average net moment [21, 22]. EDL-MF based on 4.4 nm sized NiFe₂O₄ nanoparticles exhibit a substantial particle surface disorder and the resulting magnetization does not follow a simple single-domain particle model [23]. Evidence for spin-glass-like behavior of surface spins in g-Fe₂O₃ particles has also been reported using quasi-elastic neutron scattering [24] and FMR [25] measurements.

However, the magnetic behavior of Cu- and Zn-based samples exhibited in Fig. 3 shows that, in both cases the solution magnetization tends toward and nearly reaches the saturation. This typical superparamagnetic behavior allows the use of the independent moment model since the magnetization is proportional to the volume fraction F of magnetic nanomaterial. Furthermore, in the limit of high fields, a simple estimation of the saturation magnetization of the magnetic particles can be made. Then, from the complete analysis of these curves, it has been deduced [14], the particles mean magnetic size and polydispersion. The results are listed in Table 2.

Figure 3.
Log-log representation of the normalized magnetization M/F as a function of the applied magnetic field H. The full line is the best fit obtained by using the Langevin formalism coupled with a log-normal distribution (see Table 2 for the resulting parameters size distribution).

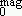Table 2: Mean nanoparticle size deduced from X-ray diffraction D_XR, magnetic size D and polydispersity s^mag deduced from magnetization measurements and compared to the respective birefringence ones D 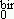and s^bir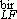. D and D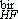 are the sizes determined from the low field analysis and the high field one.

IV Magneto-optical behavior

Birefringence Langevin formalism. Isotropic at zero applied field, magnetic fluid solutions become optically active when the field is turned on, due to some optical anisotropy along the magnetic easy axis of particles. For a magnetic solution of volume fraction F of independent polydisperse particles, the Langevin formalism gives the static field-induced birefringence at a temperature T as [6, 8, 13]:

where x = m

H/

k

_B

T is the Langevin parameter,

L

₂(x) = 1 - 3

L

₁(x)/x is the second Langevin function,

L

₁(x) being the well known first Langevin function. D

n

₀ corresponds to the optical anisotropy (shape anisometry and/or magnetic anisotropy) of one particle in suspension and slightly depends on the particle size [13].The particles diameters distribution is generally well described by a log-normal law:

where

D is the particle diameter,

s is the standard deviation and ln

D

₀ corresponds to the mean value of ln

D. The moments of the log-normal size distribution function are defined by:

Since

m

_S is determined by magnetization measurements, the curve D

N(

H)/F therefore reduces to a function of two parameters

D

₀ and

s if D

n

₀ can be evaluated. Moreover, following the analyses made in references [4] and [13], a crossing of the results obtained by using the whole birefringence curve with those obtained by using both the limits of low and high fields allows a good determination of the size distribution parameters. For high fields, 1 - 3[

L

₁(x)/x] = 1 - (3/x) and the solution birefringence can be linearly written as a function of 1/

H as:

For low fields, 1 - 3[L₁(x)/x] = x²/15 and the solution birefringence is proportional to H²:

Both equations show that the high field diameter is related to the third moment of the log-normal size distribution whereas the low field one corresponds to a higher moment of the distribution. Furthermore, the high fields analysis allows a simple determination of Dn₀.

Birefringence measurements. The external-field induced birefringence is measured up to a magnetic field about 1.5 × 10³ kA m^-1, by encapsulating magnetic fluid samples in non-birefringent glass cells a few hundred micrometers thick and using the conventional set up well described in references 13 and 26. When the magnetic field is switched on, the ferrofluid cell behaves as a birefringent plate characterized by a phase-lag j related to the birefringence of the sample of thickness e by j = 2pe Dn/l where l is the wavelength of the incident light. In our experiments, the detection device includes a photoelastic optical modulator and a lock-in amplifier which compares the detected signal from the photocell to the reference signal from the modulator. Then, the component at pulsation w of the transmitted light intensity I_w is proportional to sinj. If the sample thickness and the volume fraction F of nanomaterial are well chosen, several oscillations occur as it can be seen on Fig. 4 which shows the variations of I_w as a function of the applied field in the case of Zn- based magnetic fluid sample (F = 0.75%).

Figure 4.
Component I_w at pulsation w of the transmitted light intensity as a function of the applied field for Zn-based sample. I_w is proportional to senj.

The corresponding birefringence variations can easily be deduced from such measurements and the birefringence data are plotted in linear coordinates in Fig. 5a and Fig. 5b for Cu- and Zn-based samples respectively. The same qualitative behavior is observed for all our samples: Dn is an increasing function of the applied field and tends toward the saturation at our maximum field value. Moreover, as it can be seen on the insets of Figs. 5a and 5b, the birefringence is proportional to F showing, as expected for the values of F used in our experiments, that the measured birefringence is related to a single-particle effect. Indeed the coincidence of the data when normalized by the volume content of nanoferrite confirms the applicability of the independent particle model described in the beginning of this section. To determine the saturation behavior of Dn, the results are exhibited in Fig. 6a and Fig. 6b in double-logarithmic coordinates where the full line is the result of a best fit obtained by using equations 1 and 2. Fig. 7a and 7b present, in linear coordinates, the high field data (H > 500 kA m^-1) in such a manner that Dn₀ is determined by the value of Dn/F when 1/H tends toward zero. Furthermore, the insets of both Figures illustrate, in log-log representation, the low field behavior (H < 10 kA m^-1) of Dn proportional to H². This H² variations also indicates that at low fields, the birefringence samples comes from individual particles.

Figure 5a.
Birefringence Dn and normalized birefringence Dn/F (inset) of copper ferrite samples as a function of the applied magnetic field. (

Figure 5b.
Birefringence Dn and normalized birefringence Dn/F (inset) of zinc ferrite samples as a function of the applied magnetic field. (

Figure 6a.
Log-log representation of the normalized birefringence Dn/F of Cu-based samples as a function of the applied magnetic field. The full line is the best fit obtained by using eq. (1) (see Table 2 for the resulting parameters size distribution).

Figure 6b.
Log-log representation of the normalized birefringence Dn/F of Zn-based samples as a function of the applied magnetic field. The full line is the best fit obtained by using eq. (1) (see Table 2 for the resulting parameters size distribution).

Figure 7a.
High field analysis of birefringence data for Cu-based samples. The inset illustrates the low field behavior Dn µ H².

Figure 7b.
High field analysis of birefringence data for Zn-based samples. The inset illustrates the low field behavior Dn µ H².

Using both the limits of low and high fields, one can also obtain the size distribution parameters. Then a crossing of these results with those obtained by using the whole birefringence curve allows a good determination of the nanoparticle size and the polydispersion. In such a context, the analysis of our birefringence curves gives the results summarized in Table 3, where we compare D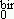, the mean value of D deduced from the whole curve, with 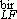D = D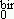exp(6 s²) and 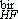D = D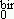exp(1.5 s²), the averaged values of D obtained from the low-field and high-field analyses respectively. As it can be seen, the standard deviations s^bir are close to those found from magnetization measurements (s^mag) whereas is significantly larger than showing as expected that the optical birefringence is more sensible to large particles. In the case of Cu-based samples, the difference between the deduced averaged values of the nanoparticle sizes is larger due to the quite broad size distribution (s = 0.5) when compared to Zn-based ones (s = 0.3) and is directly related to the synthesis process.

Table 3:
Saturation magnetization and optical anisotropy of ferrite nanoparticles (chemically coprecipitated) with their relevant references.

Finally, Table 3 summarizes the saturation magnetization and the optical anisotropy values of ferrite nanoparticles, all obtained by the same coprecipitation method in order to compare the birefringence levels of corresponding ferrofluid solutions. As it can be seen, our new EDL-MF samples present a comparable optical level to that of more common magnetic fluids showing that they also could represent good precursors for applied biological purposes.

V Conclusion

EDL-MF based on copper and zinc ferrite nanoparticles have been successfully synthesized. The particles crystallographic structure has been checked by using X-rays diffraction and identified as spinel-type. The magnetic behavior of such ferrofluid solutions is typically superparamagnetic and can be readily interpreted, in the low concentration range investigated here, using a simple single-domain particle Langevin model. In the same way, their magneto-optical birefringence has been measured in the dilute regime and is related to a single particle effect. In the investigated range of magnetic fields, the Langevin birefringence formalism well works and it has been possible to determine the parameters of the size distribution as well as the optical anisotropy of one particle in solution. Our results show that by the field-induced birefringence level, copper and zinc ferrite based MF are comparable to usual ones. Due to their reduced iron content, such magnetic colloids would represent a new alternative for biological applications. In future, it will be interesting to investigate their optical properties from a dynamic point of view. In addition, optical birefringence measurements performed on Ni-, Cu- and Zn-based EDL-MF samples synthesized with nanoparticles of different sizes are in progress.

Acknowledgments

The authors are greatly indebted to Dr. Itri (USP) for X-ray diffraction measurements. They also thank the Brazilian agencies CNPq/Pronex, CAPES, FAPDF and FAPESP for their financial support.

[17] ASTM n^o 25-0283 (CuFe₂O₄) and 22-10¹² (ZnFe₂O₄).

• [1] R. E. Rosensweig, Ferrohydrodynamics, (Cambridge University Press, New York, 1985).
• [2] Magnetic Fluids and Applications Handbook, edited by B. Berkovski (Begell House Inc. Publ., New-York, 1996).
• [3] F. A. Tourinho, J. Depeyrot, G. J. da Silva, M. C. F. L. Lara, Braz. J. Phys. 28, 413 (1998).
• [4] H. W. Davies, J. P. Llewellyn, J. Phys. D12, 311 (1979).
• [5] J. -C. Bacri, R. Perzynski, D. Salin, V. Cabuil, R. Massart, J. Magn. Magn. Mater. 62, 36 (1986).
• [6] S. Neveu-Prin, F. A. Tourinho, J. -C. Bacri, R. Perzynski, Colloids Surf. A80, 1 (1993).
• [7] E. Hasmonay, J. Depeyrot, M. H. Sousa, F. A. Tourinho, J. -C. Bacri, R. Perzynski, J. Magn. Magn. Mater. 201, 195 (1999).
• [8] J. -C. Bacri, V. Cabuil, R. Massart, R. Perzynski, D. Salin, J. Magn. Magn. Mater. 65, 285 (1987).
• [9] P. C. Scholten, IEEE Trans Mag. 16, 221 (1980).
• [10] R. Itri, J. Depeyrot, F. A. Tourinho, M. H. Sousa, Eur. Phys. J. E 4, 201 (2001).
• [11] S. Taketomi, Jpn. J. Appl. Phys.22, 1137 (1983).
• [12] E. Dubois, Ph. D. thesis, Université Pierre et Marie Curie, Paris (1997).
• [13] E. Hasmonay, E. Dubois, J. -C. Bacri, R. Perzynski, Yu. L. Raikher, V. I. Stepanov, Eur. Phys. J. B 5, 859 (1998).
• [14] M. H. Sousa, F. A. Tourinho, J. Depeyrot, G. J. da Silva, M. C. F. L. Lara, J. Phys. Chem. B 201, 1168 (2001).
• [15] A. Halbreich, J. Roger, J.-N. Pons, M. F. Da Silva, E. Hasmonay, M. Roudier, M. Boynard, C. Sestier, A. Amri, D. Geldweth, B. Fertil, J.-C. Bacri, D. Sabolovic, in Scientific and Clinical Applications of Magnetic Carriers, U. Häfeli, W. Schüt, J. Teller, M. Zborowski (Eds), Plenum Press, New York, 1997, p 399.
• [16] International Tables for X-ray Crystallography (Kynoch Press, Birmingham, England, 1968).
• [18] C. Hammond, The Basics of Crystallography and Diffraction (Oxford University Press, New York, 1997), p 145.
• [19] R. W. Chantrell, J. Popplewell, S. W. Charles, Physica 86, 1421 (1977).
• [20] J. -C Bacri, R. Perzynski, D. Salin, V. Cabuil, R. Massart, J. Magn. Magn. Mater. 62, 36 (1986).
• [21] R. H. Kodama, J. Magn. Magn. Mater. 200, 359 (1999).
• [22] R. H. Kodama, A. E. Berkowitz, E. J. McNiff Jr., S. Foner, Phys. Rev. Lett. 77, 394 (1996).
• [23] E. Hasmonay, J. Depeyrot, M. H. Sousa, F. A. Tourinho, J. -C. Bacri, R. Perzynski, Yu. L. Raikher, I Rosenman, J. Appl. Phys. 88, 6628 (2000).
• [24] F. Gazeau, E. Dubois, M. Hennion, R. Perzynski, Yu. L. Raikher, Europhys. Lett. 40, 575 (1997).
• [25] F. Gazeau, J. -C. Bacri, F. Gendron, R. Perzynski, Yu. L. Raikher, V. I. Stepanov, E. Dubois, J. Magn. Magn. Mater 186, 175 (1998).
• [26] C. Y. Matuo, A. Bourdon, A. Bee, A. M. Figueiredo Neto, Phys. Rev. E 56, 1310 (1997).

Publication Dates

• Publication in this collection
  27 Mar 2002
• Date of issue
  Sept 2001

History

• Received
  27 May 2001