Abstract
The conditions required for efficient current drive in a weakly resistive plasma column, subject to a double helix traveling magnetic field, are examined in detail by using a simple non-linear Ohm's law for the plasma. In agreement with previous numerical work on the subject by Bertram [5], it is shown that field penetration is indeed strongly limited when large external bias longitudinal magnetic fields are used. However, there is a range of small external bias fields that allow for significant penetration when reasonable driving fields are used. This should be of interest for sustaining reversed-field pinches and toroidal screw pinches.
REGULAR ARTICLES
Double-helix current drive revisited
Roberto A. ClementeI; Ricardo FarengoII
IInstituto de Física Gleb Wataghin, Universidade Estadual de Campinas, 13083-970 Campinas, SP, Brazil
IICentro Atômico Bariloche and Instituto Balseiro, 8400 S.C. de Bariloche, RN, Argentina
ABSTRACT
The conditions required for efficient current drive in a weakly resistive plasma column, subject to a double helix traveling magnetic field, are examined in detail by using a simple non-linear Ohm's law for the plasma. In agreement with previous numerical work on the subject by Bertram [5], it is shown that field penetration is indeed strongly limited when large external bias longitudinal magnetic fields are used. However, there is a range of small external bias fields that allow for significant penetration when reasonable driving fields are used. This should be of interest for sustaining reversed-field pinches and toroidal screw pinches.
1 Introduction
Among the various methods for driving continuous currents in magnetically confined plasmas, there are those based in rotating or traveling magnetic fields. They present the advantage, when compared with other schemes, that it should be possible to drive the bulk of the electrons to build up the necessary currents. Rotating magnetic fields have been proved effective in sustaining field-reversed configurations (FRC) in small devices in the past [1], and recently the scheme has attracted renewed attention from the FRC community, both from a theoretical and an experimental point of view [2-3].
Considering toroidal devices, where both poloidal and toroidal currents are necessary, a natural extension of the RMF method is the double-helix scheme, where two sets of helical coils wound around the plasma chamber and powered by a strong RF source, are employed. In the literature, there is a limited number of theoretical and experimental studies devoted to the subject [4-8], starting from the mid eighties to the mid nineties when, apparently, the subject was abandoned. The pessimistic conclusions presented by Bertram in 1988 are probably the main reason for this behavior [5]. He studied numerically the double-helix scheme using a simple model for the plasma: fixed ions, a non-linear Ohm's law for electrons, uniform density and neglected temperature effects. After examining in details two representative cases, weakly and strongly resistive plasmas, Bertram concluded (in his own words at the end of the paper): ''...strong toroidal fields do result in drastic reductions in the amount of current that can be driven. Consequently this mechanism may not provide an efficient practical method for continuous current drive when applied to a large Tokamak.''
Here, we want to examine in detail the actual conditions required for large field penetration in a weakly resistive plasma column, subject to a double helix traveling magnetic field, by using the same plasma model as Bertram. It is shown that when large external bias toroidal magnetic fields are used the penetration is strongly limited indeed. There is, however, a range of small external bias fields suitable for large penetration, when reasonable driving fields are used. This could be of interest to sustain reversed-field pinches (RFP) and toroidal screw-pinches. In the following, for clearness, we will rederive Bertram's equations introducing some different notation and correcting some misprints in Eqs. (6) and (10) of his paper.
2 Helical Formalism
Let us consider an infinite plasma column of radius a, subject to the action of external traveling helical magnetic fields varying like exp i(q + kz - wt) and a uniform static longitudinal magnetic field B0 . Ions will be considered immobile, electron inertia will be neglected together with thermal effects and density gradients, in such a way that the following Ohm's law is appropriate:
where  =
=  being n, m, -e, u and n the electronic density, mass, charge, velocity and collision frequency respectively; n and n will be assumed constants. Moreover, displacement current densities will also be neglected in such a way that Ampere's law can be written as:Ñ × B = m0J. Faraday's law Ñ × E = - ¶B/¶t will be also used.
being n, m, -e, u and n the electronic density, mass, charge, velocity and collision frequency respectively; n and n will be assumed constants. Moreover, displacement current densities will also be neglected in such a way that Ampere's law can be written as:Ñ × B = m0J. Faraday's law Ñ × E = - ¶B/¶t will be also used.
The treatment can be simplified by introducing non-dimensional helical coordinates x1 = x = r/a, x2 = q + kz and x3 ignorable, with unit vectors ê1 = êr, ê2 = (êq + hxêz) and ê3 = (êz - hxêq)/
and ê3 = (êz - hxêq)/ , where h = ka. A generic vector can be expressed as C = C1êr + (C2ê2 + C3ê3)/
, where h = ka. A generic vector can be expressed as C = C1êr + (C2ê2 + C3ê3)/ with C2 = Cq + hxCz and C3 = Cz - hxCq quasi-helical components [5]. Alternatively Cq = (C2 - hxC3)/(1 + h2x2) and Cz = (C3 + hxC2)/(1 + h2x2).
with C2 = Cq + hxCz and C3 = Cz - hxCq quasi-helical components [5]. Alternatively Cq = (C2 - hxC3)/(1 + h2x2) and Cz = (C3 + hxC2)/(1 + h2x2).
All quantities of interest will be assumed to be the sum of a steady part, indicated by a subscript 0, depending only on x and an oscillating part depending on x and only on first harmonics of x2 - wt. Without loss of generality we can restrict to positive values of w, situations of paramagnetism or diamagnetism, with relation to the externally applied bias toroidal magnetic field, will be reproduced by proper choice of the sign of such field. It is convenient to normalize the magnetic field components with 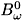 , the amplitude of the external traveling magnetic field at x = 0 in absence of plasma. Similarly, current density components will be normalized with
, the amplitude of the external traveling magnetic field at x = 0 in absence of plasma. Similarly, current density components will be normalized with 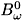 /m0a. In the following, non-dimensional components of the magnetic field and current density will be indicated with a symbol '' ~ ''.
/m0a. In the following, non-dimensional components of the magnetic field and current density will be indicated with a symbol '' ~ ''.
In complex notation, with helical symmetry, the non-dimensional time dependent magnetic field can be represented in terms of two non-dimensional scalar functions, a(x) and b(x)
and b(x) as:
as:
Correspondingly, the non-dimensional time dependent current density results:
where DÄ º  . The external traveling field in the absence of plasma corresponds to b=0 and a º acoil = - i2x
. The external traveling field in the absence of plasma corresponds to b=0 and a º acoil = - i2x (hx), where I1 is the hyperbolic Bessel function of the first kind and '' ¢ '', from here on, means derivative with respect to the argument. The amplitudes of the actual helical components of the traveling magnetic field in the absence of plasma are given by:
(hx), where I1 is the hyperbolic Bessel function of the first kind and '' ¢ '', from here on, means derivative with respect to the argument. The amplitudes of the actual helical components of the traveling magnetic field in the absence of plasma are given by:
Since DÄ acoil = 0, to our purposes it is convenient to assume that a º acoil+a. Therefore, taking into account Faraday's and Ampere's laws and ignoring contributions from second and higher harmonics of x2 - wt, it is possible to obtain for the third quasi-helical component of Ohm's law:
where 2l2 = wm0a2/h (l is the ratio between the column radius and the classical field skin depth) and d = 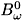 /m0newa2. Here, we adopted a different notation from that frequently used in the literature where g = 2l2d is commonly introduced. d quantifies the efficiency of the driving scheme in terms of magnetic field amplitudes and the convenience of its introduction will be evident in the results shown later on.
/m0newa2. Here, we adopted a different notation from that frequently used in the literature where g = 2l2d is commonly introduced. d quantifies the efficiency of the driving scheme in terms of magnetic field amplitudes and the convenience of its introduction will be evident in the results shown later on.
A second equation relating a and b results from considering the projection along ê3 of the curl of Ohm's law:
The zero order quantities appearing in (4) and (5) came from averaging Ohms'law, according to the rule
and also from using Ampere's law:
At x= 0 we must have a = b = 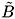 02 = 0, at x = 1 b=0 and acoil + a must be matched to the vacuum external potential arising from solutions of DÄ avac =0 , avac = acoil + Dx
02 = 0, at x = 1 b=0 and acoil + a must be matched to the vacuum external potential arising from solutions of DÄ avac =0 , avac = acoil + Dx (hx) where K1 is the hyperbolic Bessel function of the second kind and D is a complex constant. Therefore, we must have for the real and imaginary parts of a:
(hx) where K1 is the hyperbolic Bessel function of the second kind and D is a complex constant. Therefore, we must have for the real and imaginary parts of a:
The matching of the external bias field implies:
With a brilliant insight, Bertram considered the limit of full penetration as corresponding to 2l2d ® ¥ assuming 2l2d b might remain non-zero. In such case, Eq.(4) gives the current density  02 = - x/d and Eq. (5) furnishes
02 = - x/d and Eq. (5) furnishes  03 = - h(1 - 2x2)/(2 + h2)d [5]. Showing the actual possibility of driving current orthogonally to the direction of propagation of the traveling fields as well as along such direction. He also solved numerically Eqs. (4) to (9) and presented results for given l and d (or alternatively g) as functions of h using h
03 = - h(1 - 2x2)/(2 + h2)d [5]. Showing the actual possibility of driving current orthogonally to the direction of propagation of the traveling fields as well as along such direction. He also solved numerically Eqs. (4) to (9) and presented results for given l and d (or alternatively g) as functions of h using h
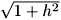 I1(h) (the external static bias toroidal magnetic field normalized to the amplitude of the second actual helical component of the external helical field at the column radius in absence of plasma) as a parameter.
I1(h) (the external static bias toroidal magnetic field normalized to the amplitude of the second actual helical component of the external helical field at the column radius in absence of plasma) as a parameter.
For plasmas of fusion interest, the parameter l should be very large. Bertram considered l=1000 and showed full penetration of the driving field when practical values of h (of order unity) are considered and d = 2.27 (g = 5.54 ·106), only in the case of vanishing external bias magnetic field. The other case, considered in more detail by Bertram, corresponds to a cold resistive plasma with l = 4 and d = .11 (or g = 3.52), showing appreciable penetration only when the driven currents are diamagnetic and the normalized (according to his rule) external bias longitudinal field is unity (correspondingly the longitudinal field at the center of the plasma column is practically vanishing).
3 Results and Discussion
Here, we want to analyze in more detail the conditions for large penetration at large l and determine the range of values of the external field where this is possible. For large penetration it should be expected that |br,i| << |acoil| = 2x (hx) . In such case, one can look for steady current density quasi-components corresponding to:
(hx) . In such case, one can look for steady current density quasi-components corresponding to:
In the case of small deviation from the limit of full penetration, we can also assume:
where e2,3 can be interpreted as a kind of slip factors (percentual deviation of electron velocities from the full penetration case) assumed small. e2,3 can be easily estimated from the real parts of Eqs. (4) and (5) when l is large:
and
Equations (15) must be integrated subject to the condition  = 0. Consistency with the smallness assumption for e2,3 , allows considering all quantities in the right hand side of Eqs. (14) and (15) as of zero order in e2,3 . Consequently br can be computed directly from Eq.(13), as:
= 0. Consistency with the smallness assumption for e2,3 , allows considering all quantities in the right hand side of Eqs. (14) and (15) as of zero order in e2,3 . Consequently br can be computed directly from Eq.(13), as:
Similarly, from Eq. (12) it results:
As it can be appreciated ar and br are of order (ld)-2, in such a way that this procedure is not applicable to the resistive case considered by Bertram (ld = 0.44). The same scaling does not apply to ai and bi, since to zero order in e2,3 the following Eqs. result:
Equations (18) and (19) show that ai and bi are of similar order and considerably larger than ar and br when l >> 1, depending also on 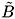 02,3 . To compute
02,3 . To compute 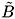 02,3 it is convenient to use the cylindrical components of the current densities to zero order in e2,3 :
02,3 it is convenient to use the cylindrical components of the current densities to zero order in e2,3 :
from which the corresponding helical quasi-components can be easily obtained as:
In the above expressions C is a real constant related to the external value of the bias magnetic field 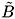 0 = (
0 = (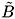 03(1) + h
03(1) + h
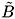 0q(1)| = |B0q(a)/
0q(1)| = |B0q(a)/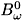 | = h/2d(2 + h2) indicating that small values of d correspond to a better efficiency in terms of magnetic amplitudes.
| = h/2d(2 + h2) indicating that small values of d correspond to a better efficiency in terms of magnetic amplitudes.
The real and imaginary parts of b tend to vanish when h tends to zero or infinite, independently of the values of l and d. However, since in such cases one or both of the driven currents also tend to vanish, the interesting cases correspond to h of order unity. This sets serious constraints on the conditions needed to justify the proposed procedure, in the sense that C must always be sufficiently small.
When l >> 1 our scaling is easily satisfied if d >> 1. When d << 1, the scaling can not be satisfied in general for ai and bi, this generate large slip factors invalidating the proposed procedure. However, when d is of order unity our scaling can be satisfied in a convenient range of the constant C. We want to emphasize that this is just the situation for the low resistivity case, l=1000 and d = 2.27, considered by Bertram. To investigate this regime we integrated Eqs. (17-19) numerically using (16) and (20) and satisfying their boundary conditions. In Figs. 1 and 2 we show ar , br and ai ,bi corresponding to l=1000, with h =  and C=-1 (vanishing longitudinal bias field). As it can be seen, all the functions are effectively small when compared with 2x
and C=-1 (vanishing longitudinal bias field). As it can be seen, all the functions are effectively small when compared with 2x (hx), in such a way that no appreciable slip factors result. However, the scaling is even better satisfied if C is increased (diamagnetic profiles), reaching the best conditions (in terms of smallness of slip factors) when C is slightly positive, allowing to obtain good penetration at smaller values of d. Apart from a small dependence on h, when C is negative bi is positive. bi has an internal zero when C is approximately comprised between 0 and 0.4, and above C =0.4 it becomes negative. As an example, we present in Fig. 3 ai and bi for the case l=1000, d=0.227, h =
(hx), in such a way that no appreciable slip factors result. However, the scaling is even better satisfied if C is increased (diamagnetic profiles), reaching the best conditions (in terms of smallness of slip factors) when C is slightly positive, allowing to obtain good penetration at smaller values of d. Apart from a small dependence on h, when C is negative bi is positive. bi has an internal zero when C is approximately comprised between 0 and 0.4, and above C =0.4 it becomes negative. As an example, we present in Fig. 3 ai and bi for the case l=1000, d=0.227, h =  and C=0.3 (screw pinch case) and in Fig. 4 the corresponding slip factors. As it can be seen, they are of the order of a few percent (the same happens for the contributions to the zero order steady current densities arising from the neglected terms in Eqs. (6) and (7)).
and C=0.3 (screw pinch case) and in Fig. 4 the corresponding slip factors. As it can be seen, they are of the order of a few percent (the same happens for the contributions to the zero order steady current densities arising from the neglected terms in Eqs. (6) and (7)).
When |C| >> 1 it is impossible to satisfy the scaling since |ai| and |bi| increase, unless larger values of d are used. This allows to understand why Bertram's results for l=1000, d = 2.27 and |h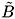 0/2
0/2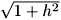 I1(h)| > 1 did not show good penetration at practical values of h. According to our procedure, such larger values of the external bias field should correspond to values of |C| > 19, for which our scaling conditions can not be attained, generating large slip factors.
I1(h)| > 1 did not show good penetration at practical values of h. According to our procedure, such larger values of the external bias field should correspond to values of |C| > 19, for which our scaling conditions can not be attained, generating large slip factors.
In general, large external bias magnetic fields, with small paramagnetism or diamagnetism, should imply large values of C and Bertram's conclusions regarding the applicability of this method to tokamak like configurations, are true since, in order to attain good penetration large values of d should be used.
However, if -1 < C < 0, the resulting configuration at large penetration corresponds to a RFP and this should be easily sustained if d = 2.27, even more, this should also be possible at d closer to unity. RFPs are more attractive than toroidal screw-pinches due to their better stability properties, moreover, they have large aspect ratios and quite flat experimental density profiles. As an example, in Figs. 5 and 6 we present results for ai, bi and the slip factors for h=1, l=1000, d=0.85 and C=-0.85. This should correspond to a RFP like equilibrium with pinch parameter Q = Bq(1)/ z = - h/(2C + 1) = 1.43 and field-reversal ratio F = B0 /
z = - h/(2C + 1) = 1.43 and field-reversal ratio F = B0 / z = (C + 1)/(C + 1/2) = - 0.43, values which are typical of RFP experiments. As it can be seen, the slip factors are reasonably small. Lower values of d generate larger slip factors and in order to assess the limits of the double helix scheme as a RFP sustainment method, full numerical calculations, including higher harmonics, should be done to avoid the limitations of the present semi-analytical study. In this regard, it is suggestive to note that in Ref. [6] second harmonics in x2 - wt were taken into account in the numerical solution of the resistive case l=4, with h=0.8 and d changing from 0 to 0.625, showing an increase in the driven currents. Unfortunately, Ref. [6] does not provide information about the value of the external bias field used in the computation.
z = (C + 1)/(C + 1/2) = - 0.43, values which are typical of RFP experiments. As it can be seen, the slip factors are reasonably small. Lower values of d generate larger slip factors and in order to assess the limits of the double helix scheme as a RFP sustainment method, full numerical calculations, including higher harmonics, should be done to avoid the limitations of the present semi-analytical study. In this regard, it is suggestive to note that in Ref. [6] second harmonics in x2 - wt were taken into account in the numerical solution of the resistive case l=4, with h=0.8 and d changing from 0 to 0.625, showing an increase in the driven currents. Unfortunately, Ref. [6] does not provide information about the value of the external bias field used in the computation.
When related to present RFP experiments, d of order unity implies quite large antenna fields, of the order of some kG. This represents a high technological requirement, in terms of RF power. However, the double helix scheme deserves additional studies, both from the theoretical an the experimental point of view, since it may be a good alternative to other non-inductive current drive schemes, like wave injection and AC helicity injection (or Oscillating Field Current Drive), presently pursued by the RFP community.
Acknowledgments
One of the authors, RAC, would like to thanks partial financial support from Conselho Nacional de Desenvolvimento Cinetífico e Tecnolôgico (CNPq, Brazil). RF would also like to acknowledge support from the Agencia Nacional de Promociôn Científica y Tecnolôgica of Argentina.
Received on 15 June, 2003
- [1] W.N. Hugrass, I.R. Jones, and M.G.R. Phillips, J. Plasma Phys. 26, 465 (1981).
- [2] R.D. Milroy, Phys. Plasmas 6, 2771 (1999).
- [3] H.Y. Guo, A.L. Hoffman, R.D. Brooks, A.M. Peter, Z.A. Pietyrzyk, and S.J. Tobin, Phys. Plasmas 9, 185 (2002).
- [4] M.J. Dutch, A.L. McCarthy, and R.G. Storer, Phys. Rev. Lett. 56, 1563 (1986).
- [5] W.K. Bertram, Plasma Phys. Contr. Fusion 30, 425 (1988).
- [6] J.A. Staines and R.G. Storer, Plasma Phys. Contr. Fusion 33, 241 (1991).
- [7] E. Hotta, M. Suzuki, H. Ohta, and I. Hayashi, Japan J. Appl. Phys. 24, 110 (1985).
- [8] M.J. Dutch and McCarthy, Plasma Phys. Contr. Fusion 28, 695 (1986).
Publication Dates
-
Publication in this collection
25 Nov 2005 -
Date of issue
Dec 2003
History
-
Accepted
15 June 2003 -
Received
15 June 2003


























