Trajectory effects in coulomb excitation

Trajectory effects in coulomb excitation

F. W. Fernandes; B. V. Carlson

Departamento de Física, Instituto Tecnológico de Aeronáutica, Centro Técnico Aeroespacial, 12228-900 São José dos Campos, São Paulo, Brazil

ABSTRACT

We compare the cross sections for Coulomb excitation of multiple giant dipole resonances in ²⁰⁸Pb + ²⁰⁸Pb scattering using Coulomb trajectories and straight-line trajectories that have the same point of closest approach as the Coulomb one. We find the effects of the Coulomb deflection relative to the straight line trajectory to be small at incident energies above about 500 MeV/nucleon.

Keywords: Multiple giant dipole resonances; ²⁰⁸Pb + ²⁰⁸Pb scattering

I. INTRODUCTION

Coulomb excitation has proven itself as an important tool for studying the structure of both stable and exotic nuclei.[1-4] The phenomenon has been well-studied in a nonrelativistic context[5] and studied perturbatively in a relativistic one[6] by Alder and Winther. More recent experimental studies have considered multiple Coulomb excitation at relativistic energies.[2-4]

Many calculations of high-energy Coulomb excitation include the effects of Coulomb deflection, but only through the effective impact parameter used in a straight-line trajectory.[7-11] The curvature of the trajectory is usually not taken into account. The curvature of the Coulomb trajectory increases the distance between the projectile and target, relative to a straight-line trajectory, and is thus expected to decrease Coulomb excitation, which is strongly dependent on the separation. In the following, we derive the semiclassical coupled-channel equations for Coulomb excitation and then use them to compare excitation cross sections obtained using straight-line and Coulomb trajectories.

II. THE SEMICLASSICAL COUPLED EQUATIONS

The scattering between two heavy ions can be well-approximated semi-classically when the wavelength of relative motion is much smaller than the length scales on which the interaction varies. We will assume this to be the case here. For a localized wave-packet, we can then determine the expectation values

directly from the classical equations of motion,

In the following, we reduce the coupled wave equations for Coulomb excitation to coupled equations for the average trajectory and for the occupation amplitudes of the ground and excited states.

We begin with the Schrödinger equation for the relative and internal motion,

where h(a) is the Hamiltonian of the internal degrees of freedom, represented by a, U₀(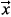) is a complex optical potential that depends on the relative coordinate alone and V_c(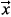,a) is the interaction coupling the relative and internal motion. We will assume that the Coulomb-excited states can be expressed as eigenstates of this Hamiltonian,

with e_n being the energy of the excited state |n ñ . For uniformity, we represent the ground state as |0 ñ with energy e₀.

We write the wavefunction of the system as a linear combination of the ground and excited states,

where exp[S(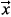,t)] describes the average relative motion and a_n(t) is the occupation amplitude of state |nñ. Before the collision, as t ® - ¥ and |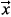| ® ¥, only the ground state is occupied, so that

Substituting the wavefunction Y(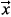,t) in the Schrödinger equation and taking the matrix element of the state á m|, we obtain

where we have defined

To isolate the equation of relative motion, we multiply the above expression by (t) and sum over m. We obtain

where we assume that

We can rewrite this equation as,

by defining the contribution of the coupling to the potential for relative motion as,

where we have used Eq. (7) to obtain

and thus

We observe that

_c(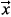,t) is real and the coupling matrix V_mn(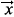) is hermitian when the coupling potential V_c(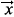,a) is real.

We write the phase S(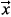,t) as an expansion in and retain only the first term,

When this is substituted in the equation for the relative motion, Eq.(8), we find, to order 0 in ,

We separate this into its real and imaginary parts,

and

If we neglect the term (ÑS_i)² in the first of these, it becomes the Hamilton-Jacobi equation, the solution of which provides the trajectory, 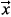(t) and (t) = ÑS_r.

Substituting (t) in the second equation, we have

which yields

S_i(t) = – Im [U₀(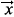(t),t)]dt.

The factor S_i(t) furnishes absorption along the trajectory due to the imaginary part of the optical potental U₀.

To obtain the coupled equations for the occupation amplitudes, we multiply Eq. (8) by a_m(t) and subtract it from Eq. (5).

The expression that results can be reduced to

Defining

and substituting in the previous equation, we obtain

which is the equation we solve numerically to obtain the occupation amplitudes. Since the cross sections depend on the occupation probabilities rather than the amplitudes, the overall phase factor provided by the real potential

_c(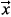(t),t) is irrelevant and can be ignored. The trajectory dependence of the occupation amplitudes can be represented as a dependence on the impact parameter 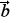. We then obtain the cross section for excitation of the state n by integrating the product of the absorption factor due to S_i and the asymptotic occupation probability of state n over the impact parameter,

III. COMPARISON BETWEEN LINEAR AND COULOMB TRAJECTORIES

The Coulomb trajectory for relative motion between a pair of ions of reduced mass µ and charges Z_P and Z_T satisfies

where p_r is the radial component of the relative momentum, L the conserved angular momentum and E the center-of-mass energy.

We can rewrite this in terms of the impact parameter b as

The minimum value of the radial distance between the ions r_min occurs where the radial momentum p_r = 0. In a head-on collision, for which b=0, this is

It can be easily shown that for arbitrary values of the impact parameter, the minimum separation is given by

r_min(b) = a + .

We perform straight-line Coulomb excitation calculations using the effective trajectory for which the minimum separation is the same as that of the Coulomb trajectory, as shown in Fig. 1. This is done by using a b_eff(b) = r_min(b) in the straight-line trajectory calculation of the the damping factor and occupation probabilities in the expression for the cross sections, Eq. (13) (but not in the area d²b). The additional effects of the Coulomb trajectory will then be due to its curvature relative to the straight line one, as illustrated in Fig. 1.

In the numerical calculations, we use the instantaneous Coulomb interaction and a dipole coupling interaction,

where (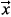) is the electric field and the isovector dipole operator of the nucleus ²⁰⁸Pb, with the dipole strength given by the energy-weighted sum rule. The excited states were assumed to be harmonic with the first excited state at 13.4 MeV. We used the São Paulo potential[12] for the real part of the optical potential and an imaginary part given by 0.78 times the real part. We note however that the real part of the nuclear potential plays an extremely limited role in the calculations shown here. The important contributions to the scattering come from the Coulomb deflection and the absorption due to the imaginary part of the optical potential. The latter was included in both the Coulomb and straight-line trajectory calculations.

Our results, as a function of the incident energy per nucleon, are shown in Fig. 2. There, we present calculations in which the excited states are stable and others in which they have non-zero widths. In both cases, as expected, we find the excitation cross sections to be smaller when the trajectory is a Coulomb one. The single giant dipole resonance (GDR) cross section is almost identical for straight-line and Coulomb trajectories at energies above about 500 MeV/nucleon. In the case of zero width, the GDR cross section for a Coulomb trajectory is about 20% below its straight-line value at 100 MeV/nucleon and about a factor of two smaller at 50 MeV/nucleon. The deviation between the the two GDR cross sections is much smaller in the case of states with widths.

The discrepancy between the cross sections obtained with Coulomb and straight-line trajectories increases with the number of modes excited. At an incident energy of 500 MeV/nucleon, the difference between the two double giant dipole cross sections is about 5% and for the triple giant dipole cross sections is about 15%. These differences are even larger at lower energies and are of about the same order of magnitude for states with and without widths.

In conclusion, we can say that the Coulomb trajectory corrections are negligible for the one and two giant dipole resonance cross sections in the incident energy range in which they have been observed (above about 600 MeV/nucleon).[2,4] These corrections become more important at lower incident energies and should certainly be taken into account at energies below about 200 MeV/nucleon.

BVC aknowledges partial support from FAPESP and the CNPq.

Received on 18 March, 2006

• [1] C. A. Bertulani and G. Baur, Phys. Rep. 163, 299 (1988).
• [2] H. Emling, Progr. Part.Nucl. Phys. 33, 792 (1994).
• [3] Ph. Chomaz and N. Frascaria, Phys. Rep. 252, 275 (1995).
• [4] T. Aumann, P.F. Bortignon, and H. Emling, Ann. Rev. Nucl. Sci 48, 351 (1998).
• [5] K. Alder and A. Winther, Coulomb Excitation, (Academic Press, New York, 1965).
• [6] A. Winther and K. Alder, Nucl. Phys. A 319, 518 (1979).
• [7] C. A. Bertulani, L. F. Canto, M. S. Hussein, and A. F. R. de Toledo Piza, Phys. Rev. C 53, 334 (1997).
• [8] B.V. Carlson, L.F. Canto, S. Cruz-Barrios, M.S. Hussein, and A.F.R. de Toledo Piza, Phys. Rev. C 59, 2689 (1999).
• [9] B.V. Carlson, L.F. Canto, S. Cruz-Barrios, M.S. Hussein, and A.F.R. de Toledo Piza, Ann. Phys.(N.Y.) 276, 111 (1999).
• [10] B.V. Carlson, M.S. Hussein, A.F.R. de Toledo Piza, and L.F. Canto, Phys. Rev. C 60, 014604 (1999).
• [11] M.S. Hussein, B.V. Carlson, and L.F. Canto, Nucl. Phys. A 731, 163 (2004).
• [12] L.C. Chamon, B.V. Carlson, L.R. Gasques, D. Pereira, C. De Conti, M.A.G. Alvarez, M.S. Hussein, M.A. Cândido Ribeiro, E.S. Rossi Jr., and C.P. Silva, Phys. Rev. C 66, 014610 (2002).

Publication Dates

• Publication in this collection
  13 Apr 2007
• Date of issue
  Dec 2006

History

• Received
  18 Mar 2006