Diffractive physics at the LHC
G. Matthiae
Università di Roma II and Sezione INFN, Roma, Italy
Received 7 January, 2000
I Introduction
TOTEM [1], [2] is an experiment dedicated to the measurement of the total cross section, elastic scattering and diffraction dissociation at the Large Hadron Collider (LHC) which is now being built at CERN.
The total cross section will be measured with the luminosity independent method based on the simultaneous measurement of low momentum transfer elastic scattering and of the rate of inelastic interactions with fully inclusive trigger.
Elastic scattering events will be detected with the Roman pot technique using a suitable optics obtained by properly tuning the quadrupoles in the intersection region. The system of dipoles foreseen in the intersection region to first combine and then separate the proton beams will be used to measure the momentum of the protons which are diffractively scattered.
II The Physics Programme
An overall view of the physics programme of TOTEM is outlined in this Section where, together with a compilation of data, also the predictions of various models at the LHC energy are discussed.
II.1 The Total Cross Section
A compilation of the total cross sections for proton-proton and proton-antiproton collisions at high energy is shown in Fig.1. Data on both pp and 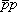 exist only up to the maximum energies of the ISR (
exist only up to the maximum energies of the ISR ( = 62 GeV). At these energies the pp and
= 62 GeV). At these energies the pp and 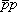 cross sections tend to approach each other. At higher energies we have data only for
cross sections tend to approach each other. At higher energies we have data only for 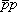 ( from the SPS and Fermilab Colliders) but results on pp collisions at
( from the SPS and Fermilab Colliders) but results on pp collisions at  = 500 GeV are soon expected from RHIC.
= 500 GeV are soon expected from RHIC.
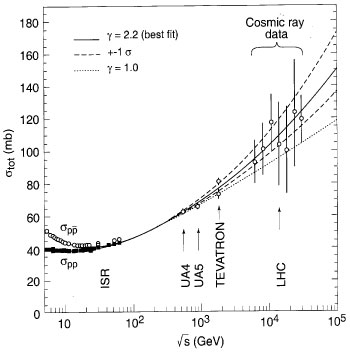
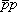 and pp scattering is shown together with the prediction of the dispersion relations fit of Ref..[3]. The high-energy behavior is described by the term (logs)g. The best fit (solid line) corresponds to g = 2.2. The region of uncertainty is delimited by the dashed lines. The result obtained with g = 1 is shown as a dotted line.
and pp scattering is shown together with the prediction of the dispersion relations fit of Ref..[3]. The high-energy behavior is described by the term (logs)g. The best fit (solid line) corresponds to g = 2.2. The region of uncertainty is delimited by the dashed lines. The result obtained with g = 1 is shown as a dotted line. A question which has been debated for a long time is whether stot increases as logs or (logs)2. The solid line in Fig.1 represents the result of a recent dispersion relation fit[3] which is based on measurements of stot and of the parameter r (ratio of the real to the imaginary part of the forward amplitude) in the c.m.s. energy interval 5 £  £ 546 GeV. The high-energy dependence of the total cross section was described by the term (logs/s0)g with s0 = 1 GeV2. The best fit gives g = 2.2 ± 0.3.
£ 546 GeV. The high-energy dependence of the total cross section was described by the term (logs/s0)g with s0 = 1 GeV2. The best fit gives g = 2.2 ± 0.3.
At  = 1.8 TeV, the fit predicts a value of the total cross section which lies in between the two measurements reported from Fermilab. The results of the experimental group E710/E811 seem to favour a logs increase while the CDF data favours the (logs)2 dependence.
= 1.8 TeV, the fit predicts a value of the total cross section which lies in between the two measurements reported from Fermilab. The results of the experimental group E710/E811 seem to favour a logs increase while the CDF data favours the (logs)2 dependence.
In spite of the large error on the parameter g as derived from the best fit, this dispersion relations analysis clearly favours the (logs)2 dependence with respect to the linear rise as logs. This behavior has been often referred to as a "qualitative" saturation of the Froissart-Martin [4] bound in the sense that it corresponds to the maximum rate of rise with energy which is allowed by analyticity and unitarity, while numerically actual data lie much below the bound itself.
At the LHC energy,  = 14 TeV, the fit predicts stot = 109 ± 8 mb while extrapolating as logs, one would obtain stot
= 14 TeV, the fit predicts stot = 109 ± 8 mb while extrapolating as logs, one would obtain stot 95 mb, i.e. about 15 mb less than the (logs)2 extrapolation. The measurement of TOTEM will have accuracy of about 1 mb, clearly sufficient to discriminate between the two possibilities.
95 mb, i.e. about 15 mb less than the (logs)2 extrapolation. The measurement of TOTEM will have accuracy of about 1 mb, clearly sufficient to discriminate between the two possibilities.
Information in the very high energy region can be derived from the study of the interaction of primary cosmic rays in the atmosphere. The results quoted by cosmic ray experiments [5] are shown in Fig.1. It should be mentioned, however, that the procedure used to extract the proton-nucleon cross section from the measured proton-air absorption probability is not straightforward. The actual proton-nucleon cross section in the energy region of the LHC could be substantially higher than those reported in Fig.1. This can be well accommodated in current models [6].
The total cross sections from the high energy hadron colliders are shown on an expanded scale in Fig.2.
The real part of the amplitude in the forward direction complements in an obvious way the measurement of the total cross section, which by virtue of the optical theorem, is just proportional to the imaginary part of the forward amplitude. In the energy region where the total cross section is first decreasing and then rising, the parameter r has initially a negative value but rises with energy becoming positive. If asymptotically the total cross section saturates the Froissart-Martin bound [4], i.e. if stot ~ (logs)2, then r will reach a broad maximum and then slowly decrease toward zero as p/logs. The broad maximum is expected in the c.m.s. energy region around 1 TeV.
The measurement of the real part of the amplitude near the forward direction requires the study of elastic scattering in the region of the Coulomb interference where the Coulomb and the strong interaction amplitudes are similar in magnitude. At the LHC this happens when |t| » 10-3 GeV2 corresponding to an angle of few mrad. From the experimental point of view, to find a way to detect events at such small scattering angles is a very serious challenge.
II.2 Elastic Scattering
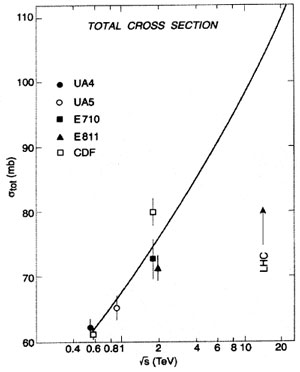
An important quantity for understanding the dynamics of high-energy collisions is the ratio sel/stot. The data on this ratio for  , which are plotted as a function of energy in Fig.3, show that sel/stot increases with energy. This observation implies that the effective "opacity" of the two colliding particles increases, although slowly, with energy. Among existing models of high-energy collisions, this behavior is most naturally explained in the impact picture of Cheng and Wu [7]. They actually predicted that at very high energy the effective radius of interaction of the two colliding hadrons would increase as logs and that the "opacity" would also increase. This leads to the expectation that asymptotically stot ~ (logs)2 and sel/stot® 1/2.
, which are plotted as a function of energy in Fig.3, show that sel/stot increases with energy. This observation implies that the effective "opacity" of the two colliding particles increases, although slowly, with energy. Among existing models of high-energy collisions, this behavior is most naturally explained in the impact picture of Cheng and Wu [7]. They actually predicted that at very high energy the effective radius of interaction of the two colliding hadrons would increase as logs and that the "opacity" would also increase. This leads to the expectation that asymptotically stot ~ (logs)2 and sel/stot® 1/2.
Most current models are able to reproduce the elastic scattering data rather well. As an example the high quality fits obtained by a Regge model [8] which includes higher order Regge exchange are shown in Fig.4 and 5
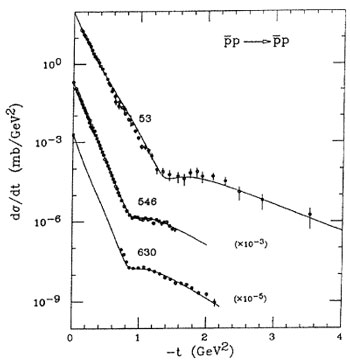
Figure 5. Proton-antiproton elastic scattering. The lines represent the fits of Ref..[8]
This effect is explained by the model of Donnachie and Landshoff [9] as due to the presence of the triple-gluon exchange mechanism. The amplitude of this process has different sign for pp and scattering. Its interference with the main amplitude which describes the diffraction peak is destructive in pp scattering, thus producing a dip, but, on the contrary, is constructive for giving rise only to a break. We then expect at LHC a dip and not a break. The cross section of the triple-gluon exchange diagram [10] in the limit of large t and very large s, decreases as the eighth power of t.
for pp and 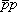 scattering, respectively. The
scattering, respectively. The 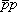 and pp data differ considerably in the region of the structure. While pp scattering shows a pronounced dip,
and pp data differ considerably in the region of the structure. While pp scattering shows a pronounced dip, 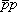 has no dip but only a shoulder.
has no dip but only a shoulder.
The data on pp scattering at large momentum transfer which are presently available indeed follow this power law for | t | ³ 3 GeV2 as shown in Fig.6.
According to this model, if the triple-gluon exchange is the dominant mechanism at large momentum transfer also at higher energies, we expect the t-distribution to be smooth at LHC, without structure. In addition the model predicts that ds/dt for fixed and large values of t is energy independent.
Other models, however, make different predictions. As an example we show in Fig.7 the prediction of the Regge model of Ref..[8]. At the LHC energy this model predicts the emergence of a diffraction pattern with several dips in contrast with the three-gluon exchange model.
The difference between the two predictions reflects a basic question on the nature of the elastic scattering of hadrons. The question is whether scattering at large momentum transfer results from a single elementary process or is dominated by a complicated interplay of various amplitudes corresponding to higher order of multiple scattering, i.e. of multiple elementary processes at low momentum transfer.
TOTEM plans to study this point in detail because the large design luminosity of the LHC allows elastic scattering to be measured up to large values of the momentum transfer, i.e. in the range 10 - 15 GeV2.
II.3 Diffraction Dissociation
The process of diffraction dissociation is closely related to elastic scattering. Single diffraction dissociation may be regarded as a two-body reaction
where one of the colliding protons is excited to a system X which then decays in a number of stable particles. To be diffractively produced, the system X must have the same intrinsic quantum numbers as the incoming proton while spin and parity may be different because some orbital angular momentum can be transferred to X in the collision.
In a high-energy collision, the mass M of the system X may take quite large values with a limitation which is imposed by the coherence condition. If p0 is the beam momentum and p the momentum of the final state proton, the mass M is given by M2 = (1 - x) s where x = p/p0. The coherence condition implies M2/s £ 0.1 High-energy data indeed provide clear evidence for diffractive production up to M2/s ~ 0.05.
The energy dependence of the ratio of the single diffraction to the total cross section is shown in Fig.8 where it is compared to the ratio of the elastic to the total cross section. The data indicate that the probability of diffraction dissociation as compared to the overall probability of interaction decreases with energy.
An important feature about diffraction dissociation to be investigated is the mass dependence of the double differential cross section  . The compilation of data at -t = 0.5 GeV2 shown in Fig.9, indicates that the mass spectrum has a 1/M2 behavior in agreement with the classical prediction of triple Pomeron exchange.
. The compilation of data at -t = 0.5 GeV2 shown in Fig.9, indicates that the mass spectrum has a 1/M2 behavior in agreement with the classical prediction of triple Pomeron exchange.
It is clear that the LHC with its very large c.m.s. energy opens new possibilities because systems with very large mass can be excited by diffraction. In fact at LHC when M2 ~ 0.05 s, the mass M is as large as 3 TeV.
After the first inclusive study of the diffraction dissociation process, it is foreseen in the TOTEM programme to proceed to more detailed investigations measuring jets at large angles in coincidence with the forward proton.
III The Experimental Method
III.1 The detection of forward protons
The measurement of elastic scattering and of diffractively produced protons at a high energy hadron collider requires observation of particles at very small angles (at the LHC, the typical angles are a small fraction of a mrad). In practice this is achieved by placing the detectors into special units mounted on the vacuum chamber of the accelerator, which have become known as "Roman pots" and were first used at the CERN ISR.
In its retracted position the Roman pot leaves the full aperture of the vacuum chamber free for the beam, as required at the injection stage when the beam is wide. Once the final energy is attained and the circulating beams are stable, the Roman pot is moved toward the machine axis by compressing the bellow, until the inner edge of the detector reaches a distance of the order of one millimeter from the beam. There is no interference with the machine vacuum.
Hadron colliders are usually operated at high luminosity for the search of rare events. To obtain high luminosity, the transverse size of the beam at the crossing point is reduced by the focusing action of quadrupoles. As a consequence the angular divergence of the beams is correspondingly increased so that a large fraction of the scattered particles remain inside the acceptance of the machine itself and are not accessible to detection.
To measure elastic scattering, the opposite scheme is actually required. The beam size at the crossing point is made relatively large while the beam divergence becomes very small. Nearly parallel beams are normally used. This implies that the b-function at the crossing point has to be large. The corresponding loss of luminosity is not a problem because the differential cross section of elastic scattering is large at small t.
The best arrangement is obtained when the machine optics corresponds to parallel-to-point focusing from the crossing point to the detectors. This has the very convenient property that measuring the particle position at the detectors allows the scattering angle to be reconstructed in a straightforward way.
The method is basically the same as the classical technique of measuring the direction of light rays by means of an optical system with a screen placed on the focal plane. The typical layout is sketched in Fig.10. The detectors are placed in the long straight section of the accelerator symmetrically on both sides of the crossing point. The behavior of the b functions for the actual high-b insertion designed for TOTEM with b*= 1100 m is shown in Fig.11.
Details about the installation of the Roman pot stations are shown in Fig.12. Each station is composed of two units. The station RP2 is used for low-t elastic scattering while the station RP1 is for large-t elastic scattering. The third station RP3 is placed behind the dipole magnet D2 which is used to bring together the beams at the crossing point. The combination of the three stations RP1, RP2 and RP3 realizes a magnetic spectrometer with momentum resolution at the level of 0.1%.
III.2 The total cross section
The best way to measure the total cross section is by means of the so called "luminosity independent" method. In fact if the machine luminosity is not known from other measurements, this will be the only method of practical use. The total cross section and the integrated luminosity  of the machine are related by the equation
of the machine are related by the equation
where Nel and Ninel are the observed numbers of elastic and inelastic interactions, respectively.
The optical theorem which relates the total cross section to the imaginary part of the forward amplitude leads to the following equation
Combining the two previous equations one may eliminate the machine luminosity and write the total cross section as a function of measurable quantities in the following way
This method is based on the simultaneous detection of elastic scattering at low t and of the inelastic interactions. The parameter r is small at high-energy, about 0.1 - 0.2, so that it does not have to be known with high precision to get an accurate value of stot.
The "luminosity independent method" was used at the ISR by the CERN-Pisa- Roma-Stony Brook collaboration, at the SPS Collider by UA4 and at the Fermilab Collider by E710/E811 and CDF.
The elastic scattering t-distribution dNel/dt is measured at small t using the Roman pot system and extrapolated to t = 0, i.e. to the so called "optical point", assuming the simple exponential dependence e-B|t| which is known to describe the data well in the very small t region.
The total number of inelastic events Ninel will be measured by the inelastic detector which fulfills two basic requirements.
-
A "fully inclusive" trigger, also called "minimum bias trigger".
-
Identification of beam-beam events against background.
At present collider energies, a sizeable fraction of the inelastic events (about 15 %) are of diffractive type, where the recoil proton, scattered at very small angles, remains inside the vacuum pipe while a few particles are emitted in the opposite hemisphere in the angular region known as fragmentation region. Events of this kind will be observed with a "single arm" trigger using the inelastic detector which provides the reconstruction of the interaction vertex from the observed charged tracks. In order to reduce the background, the recoil proton will be detected in coincidence by means of the Roman pots in the opposite hemisphere.
IV Conclusions
The discussion given by the TOTEM collaboration in Refs.[1, 2] shows that measurements of the total cross section, elastic scattering up to a large value of the momentum transfer and diffraction dissociation are indeed feasible at the LHC.
A suitable insertion optics with large b* can be designed using the machine elements already foreseen in the straight section of the accelerator. The Roman pot technique can be implemented at the LHC with detectors having resolution within reach of present technology. The system of collimation already foreseen for the LHC will provide adequate shielding of the Roman pot detectors.
The inelastic detector for the fully inclusive measurement of the inelastic interactions can be integrated at the intersection point 5. This detector will also provide absolute calibration of the machine luminosity.
Implementation of three Roman pot stations with the powerful dipole magnet D2 in between provides two forward Roman pot spectrometers placed symmetrically on both sides of the crossing point with good momentum resolution for studies of single and double diffraction dissociation and double Pomeron exchange.
References
[1] The TOTEM Collaboration, "Letter of intent", CERN/LHCC 97-49, 1997.
[2] The TOTEM Collaboration, "Technical proposal", CERN/LHCC 99-7, 1999.
[3] C. Augier et al., Phys. Lett. B 315, 503 (1993).
[4] M.Froissart, Phys. Rev. 123, 1053 (1961). A. Martin, Nuovo Cimento 42, 930 (1966).
[5] R.M. Baltrusaitis et al., Phys. Rev. Lett. 52, 1380 (1984). M.Honda et al., Phys. Rev. Lett. 70, 525 (1993).
[6] A.F.Martini and M.J. Menon, Phys. Rev. D56 (1997) 4338.
[7] H. Cheng and T.T. Wu, "Expanding Protons - Scattering at High Energies", Cambridge 1987. C. Bourrely, J. Soffer and T.T. Wu, Nucl. Phys. B 247, 15 (1984) and Z. Phys. C 37, 369 (1988).
[8] P. Desgrolard, M. Giffon and E. Predazzi, Z. Phys. C 63, 241 (1994).
[9] A. Donnachie and P.V. Landshoff, Nucl. Phys. B 231, 189 (1983) and B 267, 690 (1986).
[10] A. Donnachie and P.V. Landshoff, Z. Phys. C 2, 55 (1979) and Phys. Lett. B 387, 637 (1996).
- [3] C. Augier et al., Phys. Lett. B 315, 503 (1993).
- [4] M.Froissart, Phys. Rev. 123, 1053 (1961).
- A. Martin, Nuovo Cimento 42, 930 (1966).
- [5] R.M. Baltrusaitis et al., Phys. Rev. Lett. 52, 1380 (1984).
- M.Honda et al., Phys. Rev. Lett. 70, 525 (1993).
- [6] A.F.Martini and M.J. Menon, Phys. Rev. D56 (1997) 4338.
- [7] H. Cheng and T.T. Wu, "Expanding Protons - Scattering at High Energies", Cambridge 1987.
- C. Bourrely, J. Soffer and T.T. Wu, Nucl. Phys. B 247, 15 (1984)
- and Z. Phys. C 37, 369 (1988).
- [8] P. Desgrolard, M. Giffon and E. Predazzi, Z. Phys. C 63, 241 (1994).
- [9] A. Donnachie and P.V. Landshoff, Nucl. Phys. B 231, 189 (1983) and B 267, 690 (1986).
- [10] A. Donnachie and P.V. Landshoff, Z. Phys. C 2, 55 (1979)
- and Phys. Lett. B 387, 637 (1996).
 scattering. Its interference with the main amplitude which describes the diffraction peak is destructive in pp scattering, thus producing a dip, but, on the contrary, is constructive for
scattering. Its interference with the main amplitude which describes the diffraction peak is destructive in pp scattering, thus producing a dip, but, on the contrary, is constructive for  giving rise only to a break. We then expect at LHC a dip and not a break. The cross section of the triple-gluon exchange diagram [10] in the limit of large t and very large s, decreases as the eighth power of t.
giving rise only to a break. We then expect at LHC a dip and not a break. The cross section of the triple-gluon exchange diagram [10] in the limit of large t and very large s, decreases as the eighth power of t. Publication Dates
-
Publication in this collection
07 Jan 2002 -
Date of issue
June 2000
History
-
Received
07 Jan 2000














