Projeto de banco de filtros para estruturas adaptativas em subbandas

Projeto de banco de filtros para estruturas adaptativas em subbandas

Mariane R. Petraglia^I; Paulo B. Batalheiro^II

^IPEE/COPPE - Departamento de Engenharia Eletrônica, Universidade Federal do Rio de Janeiro, CP 68504, CEP 21945-970, Rio de Janeiro, RJ, Brasil. [e-mail]

^IILaboratório de Engenharia Elétrica, Universidade do Estado do Rio de Janeiro, CEP 20550-013, Rio de Janeiro, RJ, Brasil. [e-mail]

RESUMO

Em filtragem adaptativa, freqüentemente são propostas novas estruturas e novos algoritmos que visam a acelerar a convergência e/ou dimimuir a complexidade computacional, principalmente em aplicações que requerem o uso de um número elevado de coeficientes adaptativos. Neste sentido estruturas de filtragem adaptativa em subbandas vêm ganhando destaque pela possibilidade de se fazer a filtragem e a adaptação em uma taxa de amostragem mais baixa do que a do sinal de entrada. Recentemente, novas estruturas adaptativas em subbandas capazes de modelar exatamente qualquer sistema de resposta ao impulso finita foram propostas. Neste trabalho, as propriedades de duas destas estruturas são investigadas: na primeira, composta de um banco de análise e de filtros esparsos, não há modificação da taxa de amostragem dos sinais, enquanto que na segunda, os sinais de saída do banco de análise são criticamente sub-amostrados. Procedimentos de otimização são propostos com o objetivo de selecionar os coeficientes dos bancos de filtros que resultem em uma redu cão do erro quadrático médio (MSE) e/ou na acelera cão da taxa de convergência dos algoritmos adaptativos.

Palavras-chave: Processamento digital de sinais, filtragem adaptativa, processamento multitaxa.

ABSTRACT

In adaptive filtering, new structures and algorithms are frequently proposed with the objective of increasing the convergence speed and/or reducing the computational complexity of the conventional algorithms, mainly for applications which require a large number of adaptive coefficients. In such applications, adaptive subband structures are especially atractive since the adaptation and filtering are performed at a reduced sampling rate. Recently, new adaptive subband structures were proposed, which are able of modeling exactly any finite impulse response system. In this work the performance properties of two of these structures are investigated: in the first one, composed of an analysis filter bank and sparse subfilters, there is no sampling rate alteration, while in the second one, the ouput signals of the analysis filter bank are maximally decimated. Optimization procedures are proposed to select the filter bank coefficients of such structures, which result in a reduction of the mean-square error (MSE) and/or in an improvement of the convergence behavior of the adaptation algorithms.

Keywords: Adaptive signal processing, adaptive filtering, multirate processing.

1. INTRODUÇÃO

Estruturas de filtragem adaptativa em subbandas são atraentes em aplicações como cancelamento de ecos acústicos e equalização de canais devido às suas propriedades de aceleração da convergência do algoritmo adaptativo e redução da complexidade computacional para filtros longos (Gilloire, 1987), (Yasukawa et alii, 1987), (Kellermann, 1988). Em Gilloire e Vetterli (1992), foi proposta uma estrutura com decimação máxima capaz de fazer uma modelagem quase exata de sistemas com resposta ao impulso finita (FIR), através da inserção de filtros cruzados e considerando existência de aliasing somente entre bandas adjacentes. Neste caso, tanto o sinal de entrada quanto o sinal desejado são decompostos em subbandas, e o erro gerado em cada subbanda é utilizado para adaptar os respectivos filtros adaptativos relacionados à subbanda (direto e cruzados). Em Petraglia e Mitra (1993), uma estrutura em subbandas com decimação não crítica (i.e., com fator de decimação L menor que o número de subbandas M) foi estudada. Nesta estrutura, os coeficientes dos subfiltros passam a ser adaptados numa taxa L vezes menor que a do sinal de entrada, e o aliasing é diretamente relacionado ao fator de decimação (i.e., quanto maior o valor de L, maior o MSE mínimo da estrutura).

Duas novas estruturas em subbandas capazes de modelar qualquer sistema FIR foram propostas em Petraglia et alii (2000). A primeira utiliza um banco de análise sem decimação, seguido por filtros adaptativos esparsos; já a segunda, que é derivada da primeira, utiliza um banco de filtros criticamente decimado e os filtros adaptativos operam na taxa reduzida. Neste artigo vamos desenvolver métodos para o projeto de bancos de filtros para estas duas estruturas, tendo como objetivo a minimização do erro quadrático médio (MSE) final e/ou a aceleração da convergência do algoritmo adaptativo. Para tanto, vamos apresentar, na Seção 2, a estrutura em subbandas com filtros esparsos, o algoritmo de adaptação correspondente e sua análise de convergência, e o método de projeto otimizado de seu banco de filtros. Na Seção 3, a estrutura em subbandas com decimação crítica será descrita, bem como seu algoritmo adaptativo e a análise de convergência correspondente. A seguir, um método de otimização para o projeto dos bancos de filtros da estrutura com decimação crítica será proposto. Os resultados experimentais serão apresentados na Seção 4. Na Seção 5, implementações eficientes para as estruturas e as respectivas complexidades computacionais serão discutidas. As conclusões deste trabalho serão apresentadas na Seção 6.

2. ESTRUTURA ADAPTATIVA EM SUB-BANDAS COM FILTROS ESPARSOS

A estrutura adaptativa em subbandas mostrada na Fig. 1, que utiliza um banco de filtros de análise e subfiltros adaptativos esparsos, era tida como capaz de modelar somente uma classe particular de sistemas FIR (Usevitch e Orchard, 1996). Porém, como mostrado a seguir, escolhendo-se apropriadamente o banco de filtros e o número de coeficientes dos subfiltros adaptativos esparsos, a estrutura da Fig. 1 é capaz de modelar qualquer sistema FIR.

Considerando a representação polifásica do banco de análise da estrutura da Fig. 1, a matriz polifásica de dimensão M × M (Strang e Nguyen, 1996) é definida como

em que H_i,j(z) são as componentes polifásicas do tipo 1 do i-ésimo filtro de análise H_i(z) = h_i(n)z^-n, dadas por

A função de transferência implementada pela estrutura da Fig. 1 pode então ser escrita em função de H_p(z) e das funções de transferências dos subfiltros esparsos como

Em aplicações de identificação de sistemas, os coeficientes dos subfiltros esparsos G_i(z^M) são adaptados para modelar um sistema FIR desconhecido, o qual será denominado de W(z). A decomposição polifásica do tipo 1 da função de transferência do sistema desconhecido é dada por

A partir das Eqs. (3) e (4), podemos observar que a estrutura em subbandas irá modelar exatamente um sistema FIR desconhecido quando

Observando a Eq. (5) vemos que a igualdade não pode em geral ser alcançada com subfiltros G_i(z^M) causais e FIR. Porém, se

e tal que

em que I_M é a matriz identidade de dimensão M × M, a função de transferência implementada pela estrutura da Fig. 1 será

As matrizes H_p(z) e F_p(z) que satisfazem a condição da Eq. (7) correspondem às matrizes polifásicas de análise e síntese de um banco de filtros com reconstrução perfeita. A matriz polifásica do banco de síntese é definida como

em que F_i,j(z) são as componentes polifásicas do tipo 2 do i-ésimo filtro de síntese F_i(z) = f_i(n)z^-n dadas por

Portanto, utilizando um banco de filtros de análise que permita reconstrução perfeita e subfiltros adaptativos esparsos com ordem suficiente para satisfazer a Eq. (6), a estrutura da Fig. 1 implementa exatamente qualquer sistema FIR. Deve ser enfatizado que há um atraso introduzido pelo banco de filtros, o qual precisa ser considerado no algoritmo de adaptação. Para um banco de análise modulado por cosseno (Vaidyanathan, 1993) com filtro protótipo de comprimento N_p, o atraso é dado por D = N_p – M. O número K de coeficientes adaptativos não-nulos nos subfiltros esparsos G_i(z^M) deve ser no mínimo:

em que N_w é o comprimento do sistema desconhecido.

2.1. Algoritmo de Adaptação

Definindo x_i(n) como o sinal na saída do i-ésimo filtro de análise e g_i,k como o k-ésimo coeficiente não-nulo do subfiltro esparso G_i(z^M) da Fig. 1, a equação de atualização dos coeficientes adaptativos (utilizando o algoritmo LMS normalizado com minimização do erro quadrático instantâneo total) é

para i = 0,1,¼,M – 1 e k = 0,1,¼,K – 1.

Na Eq. (13), o sinal de erro e(n) é dado por

em que d(n) é o sinal desejado, y(n) é o sinal de saída da estrutura adaptativa em subbandas, e D é o atraso introduzido pelo banco de filtros. O fator de convergência para cada subfiltro esparso é inversamente proporcional à potência do sinal na saída do filtro de análise correspondente, isto é,

sendo (n) a estimativa da potência de x_i(n). A utilização de diferentes fatores de convergência na adaptação dos coeficientes dos diferentes subfiltros esparsos aumenta significativamente a velocidade de convergência do algoritmo adaptativo para sinais de entrada coloridos quando comparado ao algoritmo LMS convencional, como será mostrado nas simulações da Seção 4.1.

2.2. Análise de Convergência

Estudaremos, agora, as propriedades de convergência da estrutura em subbandas da Fig. 1, quando os coeficientes são adaptados utilizando o algoritmo adaptativo LMS normalizado apresentado na subseção anterior. Definindo o vetor do sinal de entrada como

em que C = N_p+ M(K – 1) – 1, e a matriz H_i de dimensão K × C como em (12) com a primeira linha contendo os N_p coeficientes do i-ésimo filtro de análise H_i(z) seguidos de C – N_p zeros, e as próximas linhas obtidas pelo deslocamento circular de M amostras para a direita da linha anterior, então o vetor x_i(n), que contém as amostras do sinal na saída do filtro de análise que serão pesadas pelos coeficientes não-nulos de G_i(z^M), é dado por

Definindo, a seguir, os vetores

e

a forma vetorial para a equação de atualização (13) é dada por

e a saída da estrutura adaptativa pode ser escrita como

Na Eq. (20), a matriz m contém os passos de adaptação dos diferentes subfiltros, i.e.,

em que I_K é a matriz identidade de dimensão K × K.

Tirando o valor esperado de ambos os lados da Eq. (20), assumindo sinais estacionários e que não há correlação entre o vetor de entrada x_a(n) e o vetor de coeficientes g(n) (ver ''Teoria da Independência'' em Haykin (1996)), teremos

em que = E[x_a(n)x_a(n)^T] é a matriz de auto-correlação do vetor de entrada e = E[x_a(n)d(n – D)] é o vetor de correlação cruzada entre o sinal desejado e o vetor de entrada.

Observando a Eq. (23), o desempenho da convergência do algoritmo adaptativo é governado pelos autovalores da matriz

Vamos mostrar a seguir como podemos utilizar os resultados aqui obtidos para selecionar o banco de filtros de análise para um dado sinal de entrada, melhorando a taxa de convergência do algoritmo adaptativo da estrutura da Fig. 1.

2.3. Projeto do Banco de Filtros

Nesta seção vamos descrever um procedimento de otimização para obter um banco de filtros modulado por cosseno com reconstrução perfeita que, quando utilizado na estrutura da Fig. 1, resulta numa melhor taxa de convergência para um dado sinal de entrada. A escolha de bancos de filtros modulados por cosseno deve-se ao fato destes apresentarem implementação eficiente, conforme descrito na Seção 5, e permitirem reconstrução perfeita (Vaidyanathan, 1993). Assumindo que p(n) é a resposta ao impulso do filtro protótipo P(z) de comprimento N_p de um banco de filtros modulado por cosseno de M bandas, os filtros de análise são dados por (Vaidyanathan, 1993):

em que q_k = , para 0 < k < M – 1 e 0 < n < N_p – 1. As condições necessárias e suficientes para que um filtro protótipo de comprimento N_p = 2mM (m > 1) e fase linear garanta reconstrução perfeita, para M par, são dadas por (Vaidyanathan, 1993)

em que P_k(z) são as componentes polifásicas do tipo 1 de P(z) para 0 < k < M/2 – 1. Estas restrições podem ser reescritas numa forma quadrática em função dos coeficientes do filtro protótipo levando em conta a simetria destes coeficientes (Nguyen, 1995), como mostrado a seguir:

em que

com 0 < k < M/2 – 1, 0 < n < m – 1. As dimensões de p, V_k, J e D_n são (mM × 1), (mM × m), (m × m) e (m × m), respectivamente.

Com o objetivo de reduzir o tempo de convergência do algoritmo de adaptação da Eq. (13), a função custo utilizada no procedimento de otimização, atendendo as mM/2 restrições quadráticas da Eq. (27), é dada por

com a matriz R dada pela Eq. (24). Esta matriz tem dimensão MK × MK que torna-se grande à medida em que a ordem do sistema desconhecido aumenta, resultando num problema de otimização de grande complexidade computacional e tempo de processamento. Entretanto, na prática, verificamos que podemos otimizar o filtro protótipo utilizando uma matriz R de dimensão reduzida (i.e., considerando um sistema desconnhecido de ordem reduzida, apenas no processo de otimização), sem significante degradação dos resultados. Com este procedimento de otimização o tempo de convergência da estrutura pode ser reduzido, como será mostrado nas simulações da Seção 4.1.

3. ESTRUTURA ADAPTATIVA CRITICAMENTE DECIMADA

A Fig. 2 mostra a estrutura adaptativa proposta em Petraglia et alii (2000), que foi obtida a partir da estrutura da Fig. 1, considerando a introdução de bancos de filtros de análise e síntese criticamente decimados com reconstrução perfeita após cada filtro esparso. Através das identidades nobres (Strang e Nguyen, 1996), pode-se inverter a posição dos subfiltros esparsos G_k(z^M) com o banco de análise e os decimadores. Com isso os subfiltros adaptativos G_k(z) da estrutura criticamente decimada passam a operar numa taxa M vezes menor que a taxa do sinal de entrada.

Assumindo que p(n) é um filtro protótipo de comprimento N_p e fase linear que permite reconstrução perfeita em sistemas multitaxas de M bandas modulados por cosseno, podemos relacioná-lo aos filtros dos bancos de análise e síntese, respectivamente, pelas Eqs. (25) e (32).

Os filtros H_k(z)H_k(z) que decompõem o sinal de entrada na estrutura da Fig. 2 têm respostas impulsionais dadas por

em que

Considerando que não existe sobreposição de espectros entre as respostas em freqüência dos filtros de análise não-adjacentes (H_k(z) e H_j(z), com |k – j| > 1), podemos desprezar o último termo da Eq. (33) para 1 < k < M – 2. Podemos também aproximar as respostas impulsionais dos filtros extras H_k(z)H_k+1(z) da Fig. 2 por

3.1. Algoritmo de Adaptação

A Fig. 2 mostra a estrutura criticamente decimada aplicada à identificação de sistemas, em que os coeficientes dos subfiltros G_k(z) são adaptados para modelar um sistema FIR desconhecido W(z). Para modelar exatamente um sistema FIR de comprimento N_w, o número de coeficientes de cada subfiltro adaptativo G_k(z) deve ser igual ou maior que K dado na Eq. (11). Um algoritmo baseado no método do gradiente descendente com função custo

é dado por:

em que G_k(m) e X_i,j(m) são vetores de dimensão K × 1 contendo, respectivamente, os coeficientes do k-ésimo subfiltro e as últimas K amostras do sinal X_i,jda Fig. 2. Conforme esta figura, os erros E_k(m) são dados por:

sendo D = N_p/M. O fator de convergência m_k é inversamente proporcional à soma das potências dos sinais envolvidos na adaptação dos coeficientes G_k(m), isto é,

em que P_i,j = E[(m)] pode ser estimada utilizando a seguinte recursão:

para 0 < b < 1.

3.2. Análise de Convergência

Para analisar o comportamento da convergência do algoritmo proposto foi estudada em Petraglia et alii (2000) a evolução na média do vetor de erro dos coeficientes definido como:

em que é o vetor de coeficientes ótimos da k-ésima subbanda. Foi mostrado que a velocidade de convergência do algoritmo está diretamente relacionada à relação entre os autovalores da matriz mf, em que

com os fatores m_k calculados de acordo com a Eq. (39), e f é uma matriz simétrica dada por:

com

3.3. Projeto do Banco de Filtros

O MSE da estrutura da Fig. 2 com mais de duas subbandas é da ordem da ondulação na faixa de rejeição da resposta em frequência do filtro protótipo quando são utilizados bancos de filtros com reconstrução perfeita (PR) ou quase perfeita (NPR), uma vez que tal estrutura foi derivada assumindo que não havia sobreposição entre as respostas em frequência dos filtros de análise de subbandas não-adjacentes. Filtros protótipos com PR são projetados a partir de um processo de otimização com restrições (Nguyen, 1995) que garantem erros de distorção e de aliasing muito pequenos, com prejuízo da atenuação na faixa de rejeição. Protótipos com reconstrução quase perfeita também são desenvolvidos com restrições (ver Nguyen, 1994) que garantem erro de distorção muito pequeno, com erro de aliasing maior do que os filtros PR, mas com maior atenuação na faixa de rejeição. Podemos selecionar um filtro protótipo que minimize o MSE da estrutura da Fig. 2 considerando três tipos de fontes de erro: erro de distorção, erro de aliasing, e erro devido à atenuação finita na faixa de rejeição. O MSE final será uma combinação de tais erros. Para algumas aplicações, como cancelamento de ecos acústicos, um MSE muito pequeno pode ser negociado por uma melhor taxa de convergência. Nestes casos, o filtro protótipo pode ser desenvolvido levando em conta sua influência na taxa de convergência.

Um processo de otimização não-linear sem restrições, que considera a contribuição do filtro protótipo no MSE final e na taxa de convergência, pode ser implementado para obter os bancos de filtros através da seguinte função custo:

em que a₁, a₂ e a₃ são constantes que controlam a importância de cada termo durante o processo de otimização, e g é uma pequena constante que controla a largura da faixa de transição do filtro protótipo. Os dois primeiros termos são responsáveis pela redução do MSE enquanto o terceiro termo busca reduzir a relação entre os autovalores da matriz mf. Esta matriz tem dimensão MK × MK, que se torna grande à medida em que a ordem do sistema desconhecido e/ou do filtro protótipo aumenta, resultando numa otimização com maior complexidade computacional e tempo de processamento. Entretanto, como foi feito para a estrutura com filtros esparsos, podemos efetuar a otimização considerando um sistema desconhecido de ordem reduzida, sem significante degradação dos resultados.

Quando um peso maior é dado para a última parcela da Eq. (47) (i.e., quando é desejado uma melhor taxa de convergência em detrimento do MSE), é conveniente utilizar o filtro protótipo desenvolvido pelo procedimento de otimização descrito acima somente na implementação dos filtros de análise, e otimizar o banco de síntese para reduzir o MSE final da estrutura. Um algoritmo adaptativo, tal como o algoritmo LMS, pode ser usado para ajustar os coeficientes dos filtros de síntese F_k(z) na configuração em subbandas mostrada na Fig. 3, em que o sinal desejado é uma versão atrasada do sinal de entrada.

Com o procedimento de otimização descrito nesta seção, o MSE final e/ou o tempo de convergência da estrutura criticamente amostrada pode ser significamente reduzido, como será mostrado nas simulações da Seção 4.2.

4. RESULTADOS EXPERIMENTAIS

Nesta seção serão apresentadas as simulações computacionais para o problema de identificação de sistemas considerando a estrutura com filtros esparsos da Fig. 1 e a criticamente decimada da Fig. 2.

4.1. Estrutura em Subbandas com Filtros Esparsos

Para ilustrar o comportamento da convergência do algoritmo de adaptação, mostraremos uma comparação da evolução do MSE da estrutura da Fig. 1 para sinais de entrada coloridos com dois tipos de filtros protótipos com reconstrução perfeita: o primeiro desenvolvido para maximizar a atenuação na faixa de rejeição conforme descrito em Nguyen (1995) (PR), e o segundo otimizado para acelerar a convergência do algoritmo adaptativo pelo método descrito na Seção 2.3 (PR-OTM). O sistema desconhecido é um sistema FIR de comprimento N_w = 128 e o sinal de entrada colorido foi gerado passando um ruído branco através de um filtro IIR de primeira ordem com pólo localizado em z = 0,9. No projeto dos filtros protótipos pelo método da Seção 2.3, considerou-se, somente para fins de redução do problema de otimização, N_w = 64, sem haver praticamente nenhuma alteração nos coeficientes destes filtros em relação aos obtidos com N_w = 128.

A Tabela 1 contém os comprimentos dos filtros protótipos (N_p) utilizados na implementação do banco de análise e a razão entre os autovalores da matriz R da Eq. (24) para estes protótipos e para o LMS com passo normalizado pela potência do sinal de entrada (M = 1).

Na Fig. 4 temos a evolução do MSE para o algoritmo LMS e para a estrutura em subbandas com M = 2, 4, 8 e 16 e os protótipos da Tabela 1. Os fatores de convergência m da Eq. (15) foram escolhidos de forma a obter a melhor convergência para cada caso.

Podemos observar pela Fig. 4 que o desempenho da estrutura com os filtros protótipos desenvolvidos para aumentar a taxa de convergência é significativamente melhor à medida em que o número de subbandas cresce, confirmando os resultados teóricos apresentados na Tabela 1. Observamos também que, para um dado número de subbandas, aumentar o comprimento do filtro protótipo nem sempre implica numa melhor taxa de convergência, e ainda aumenta o atraso (D) introduzido pela estrutura em subbandas.

4.2. Estrutura em Subbandas Criticamente Decimada

4.2.1. Sinal de Entrada Ruído Branco

Faremos, agora, um estudo comparativo do comportamento da convergência da estrutura da Fig. 2 com ruído branco na entrada, variando o número de subbandas (M = 2, 4, 8 e 16) e utilizando banco de filtros modulado por cosseno com três tipos de filtros protótipos: PR e NPR (obtidos de Strang e Nguyen (1996)), e otimizado pelo método descrito na Seção 3.3 (OTM). O sistema desconhecido é um sistema FIR de comprimento N_w = 1024, e um ruído branco com variância = 10^-12 foi somado ao sinal desejado. O fator de convergência m da Eq. (39) foi igual a 1/K e o fator de esquecimento (b) utilizado no cálculo recursivo da potência da Eq. (40) foi igual a 0,9. Os protótipos otimizados foram desenvolvidos de acordo com a Seção 3.3, com a₂ = 100a₁ para M = 4, 8, 16 e a₁ = a₂ para M = 2. Para mais de duas bandas, um peso maior (a₂) foi dado para o termo da Eq. (47) que controla a atenuação na faixa de rejeição com o objetivo de reduzir a sobreposição entre as respostas em freqüência dos filtros de análise não-adjacentes. Fizemos a₃ = 0, já que para ruído branco na entrada a taxa de convergência da estrutura adaptativa não pode ser melhorada (a razão entre os autovalores é próxima de um para qualquer banco de filtros com reconstrução perfeita, conforme mostrado em Petraglia et alii (200)).

A Tabela 2 contém o comprimento dos filtros protótipos(N_p) e o MSE experimental final obtidos com os protótipos PR, NPR e OTM. A Fig. 5 mostra a resposta em freqüência dos três tipos de filtros protótipos e dos filtros de análise correspondentes da estrutura com M = 4 subbandas. A Fig. 6 mostra a evolução do MSE da estrutura da Fig. 2 com M = 4 e do algoritmo LMS convencional (LMS). Da Fig. 6 e da Tabela 2, pode-se observar que uma redução significativa no MSE final da estrutura foi obtido usando um filtro protótipo dedicado.

4.2.2. Sinal de Entrada Colorido

Faremos, agora, uma comparação da evolução do MSE da estrutura em subbandas para sinal de entrada colorido com filtros protótipos desenvolvidos com reconstrução perfeita (PR) de acordo com Strang e Nguyen (1996) e otimizados (OTM) para melhorar a taxa de convergência conforme Seção 3.3. O sistema desconhecido é um sistema FIR de comprimento N_w = 880, sendo somado ao sinal desejado um ruído branco de variância = 10^-5. O sinal de entrada colorido foi gerado da mesma forma que nas simulações da Seção 4.1. No projeto do filtro protótipo pelo método da Seção 3.3, a₁ e a₂ foram ajustados para obter um MSE da ordem de -50dB (variância do ruído adicionado), e a₃ foi escolhido para que o termo correspondente na função custo (Eq. (47)) tivesse inicialmente um valor dez vezes maior que os outros termos. Os filtros de síntese foram otimizados utilizando o algoritmo LMS na configuração da Fig. 3. Os comprimentos dos filtros protótipos utilizados nas implementações dos filtros de análise e síntese foram os mesmos das simulações com ruído branco (N_p na Tabela 2).

A Tabela 3 mostra a razão entre o maior e o menor autovalor da matriz de correlação mf (Eqs. (42) e (43)), utilizando filtros protótipos com reconstrução perfeira (PR) e otimizados para acelerar a convergência do algoritmo adaptativo (OTM). Desta tabela, podemos observar que em todos os casos a razão entre os autovalores da matriz mf decresce com o número de subbandas M (M = 1 corresponde ao algoritmo LMS convencional). Para um dado número de subbandas, a utilização do filtro protótipo otimizado resulta na redução da razão dos autovalores por um fator de aproximadamente 2 em relação à utilização do banco de filtros com reconstrução perfeita.

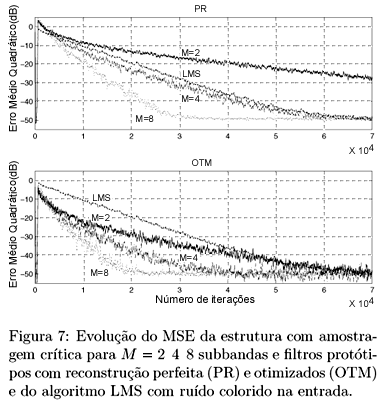
A Fig. 7 mostra a evolução do MSE para o algoritmo LMS convencional e para a estrutura em subbandas com M = 2, 4 e 8. Esta figura mostra que a taxa de convergência do algoritmo adaptativo em subbandas pode ser significativamente melhorada utilizando-se filtros protótipos selecionados através do procedimento de otimização descrito na Seção 3.3. A Fig. 8 contém a evolução do MSE da estrutura em subbandas com M = 4, para um sinal de entrada com estatísticas um pouco diferentes das do sinal utilizado no projeto do filtro protótipo otimizado (alterou-se o pólo do filtro que gera o ruído colorido para 0,95). O desempenho do algoritmo em subbandas com o filtro protótipo otimizado ainda assim foi superior ao obtido com o protótipo PR, mostrando que um exato conhecimento das estatísticas do sinal de entrada não é necessário para o projeto do filtro protótipo pelo método da Seção 3.3.

5. COMPLEXIDADE COMPUTACIONAL

Utilizando formas eficientes na implementação dos bancos de análise e de síntese modulados por cosseno (Malvar, 1992) é possível, no caso de identificação de sistemas FIR de ordens elevadas, reduzir a complexidade computacional das estruturas adaptativas em subbandas. Neste trabalho vamos considerar como complexidade computacional o número de multiplicações reais por amostra do sinal de entrada (N_mult).

Implementando a estrutura com filtros esparsos da Fig. 1 de forma eficiente (utilizando a técnica de modulação por cosseno descrita em Malvar (1992) para o banco de análise de M canais), o N_mult é dado por:

em que N_p é o comprimento do filtro protótipo e K é o número de coeficientes não-nulos de cada filtro esparso dado na Eq. (11). O primeiro termo da equação acima corresponde à implementação do banco de análise, o segundo à computação de uma transformada cosseno discreta (DCT) de tamanho M e o terceiro corresponde à filtragem e à adaptação dos filtros esparsos G_k(z^M). Considerando-se N_p << N_w, em que N_w é o comprimento do sistema desconhecido, temos:

que é igual à complexidade do algoritmo LMS convencional. Portanto, para filtros adaptativos longos, o algoritmo proposto é quase tão econômico quanto o algoritmo LMS convencional em termos de operações aritméticas. Devemos observar, no entanto, que há um aumento na quantidade de dados armazenados (da ordem do número de subbandas M).

Para a estrutura criticamente decimada da Fig. 2, o N_mult resultante, utilizando-se implementações eficientes para os bancos de filtros modulados por cosseno, é dado por:

em que K é o comprimento de cada subfiltro adaptativo (Eq. (11)). O primeiro termo corresponde à implementação dos bancos de análise e síntese, o segundo à computação de quatro DCTs, e o terceiro à filtragem e à adaptação dos filtros G_k(z). O fator M no denominador se deve ao fato de que todas estas operações são realizadas numa taxa de amostragem M vezes menor que a taxa do sinal de entrada. Substituindo K na equação anterior por (11), e considerando apenas o termo dominante, obtemos:

que é aproximadamente M/3 vezes menor que a complexidade do algoritmo LMS convencional. Neste caso, não há aumento considerável na quantidade de dados armazenados em relação ao algoritmo LMS convencional.

6. CONCLUSÕES

Neste trabalho foram propostos dois métodos para desenvolvimento de filtros protótipos para os bancos de filtros modulados por cosseno utilizados nas estruturas adaptativas em subbandas: o primeiro método leva em conta a taxa de convergência do algoritmo adaptativo de uma estrutura que utiliza filtros esparsos e o segundo permite a redução do MSE final e/ou do tempo de convergência dos algoritmos adaptativos de uma estrutura criticamente decimada. Foram realizadas simulações computacionais para os dois tipos de estruturas, nas quais os bancos de filtros foram implementados utilizando-se diferentes filtros protótipos. Os filtros protótipos otimizados pelos procedimentos propostos resultaram numa significante redução do MSE final da estrutura criticamente decimada para ruído branco como sinal de entrada, enquanto uma aceleração na taxa de convergência foi obtida para sinais de entrada coloridos tanto na estrutura com filtros esparsos quanto na estrutura criticamente decimada.

Artigo submetido em 24/09/01

1a. Revisão em 02/02/02; 2a. Revisão em 27/08/02

3a. Revisão em 23/10/02

Aceito sob recomendação do Ed. Assoc. Prof. José R. C. Piqueira

• Gilloire, A. (1987). Experiments with sub-band acoustic echo cancellers for teleconferencing. Proc. IEEE Int. Conf. Acoust., Speech, Sig. Proc., Dallas, TX, pp. 2141-2144.
• Gilloire, A. and M. Vetterli (1992). Adaptive filtering in subbands with critical sampling: analysis, experiments, and application to acoustic echo cancellation. IEEE Trans. Signal Processing, Vol. 40, no. 8, pp. 1862-1875.
• Haykin, S. (1996). Adaptive Filter Theory, 3rd. ed. Englewood Cliffs, NJ: Prentice-Hall.
• Kellermann, W. (1988). Analysis and design of multirate systems for cancellation of acoustical echoes. Proc. IEEE Int. Conf. Acoust., Speech, Sig. Proc., New York, NY, pp. 2570-2573.
• Malvar, H. S. (1992). Signal Processing with Lapped Transforms Norwell, MA: Artech House.
• Nguyen, T. Q. (1994). Near Perfect Reconstruction pseudo-QMF banks, IEEE Trans. Signal Processing, Vol. 42, pp. 65-76.
• Nguyen, T. Q. (1995). Digital filter banks design - quadratic constrained formulation, IEEE Trans. Signal Processing, Vol. 43, pp. 2103-2108.
• Petraglia, M. R. and S. K. Mitra (1993). Performance analysis of adaptive filter structures based on subband decomposition. Proc. IEEE Int. Symp. Circ. Syst., Chicago, IL, pp. 60-63.
• Petraglia, M. R., R. G. Alves and P. S. R. Diniz (2000). New subband adaptive structures with critical sampling, IEEE Trans. on Signal Processing, Vol. 48, no. 12, pp. 3316-3327.
• Strang, G. and T. Nguyen (1996). Wavelets and Filter Banks Wellesley - Cambridge Press.
• Usevitch, B. E. and M. T. Orchard (1996). Adaptive filtering using filter banks. IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing, Vol. 43, pp. 255-265.
• Vaidyanathan, P. P. (1993). Multirate Systems and Filter Banks Prentice-Hall, Englewood Cliffs, New Jersey.
• Yasukawa, H., S. Shimada and I. Furukawa (1987). Acoustic echo canceller with high speech quality. Proc. IEEE Int. Conf. Acoust., Speech, Sig. Proc., Dallas, TX, pp. 2125-2128.

Datas de Publicação

• Publicação nesta coleção
  31 Jul 2003
• Data do Fascículo
  Jun 2003

Histórico

• Aceito
  23 Out 2002
• Recebido
  24 Set 2001
• Revisado
  27 Ago 2002