Homogenisation of magneto-elastic behaviour: from the grain to the macro scale

Homogenisation of magneto-elastic behaviour: from the grain to the macro scale

Laurent Daniel^*; Olivier Hubert; René Billardon

LMT-Cachan, ENS Cachan, CNRS (UMR 8535), Université Paris 6 61 avenue du Président Wilson - 94235 CACHAN Cedex - France E-mail: [e-mail]

ABSTRACT

The prediction of the reversible evolution of macroscopic magnetostriction strain and magnetisation in ferromagnetic materials is still an open issue. Progress has been recently made in the description of the magneto-elastic behaviour of single crystals.

Herein, we propose to extend this procedure to the prediction of the behaviour of textured soft magnetic polycrystals. This extension implies a magneto-mechanical homogenisation. The model proposed is discussed and the results are compared to experimental data obtained on industrial iron-silicon alloys.

Mathematical subject classification: 74F15, 74Q05, 74Q15, 74M05, 78M40.

Key words: multiscale approach, homogenisation, magnetoelastic couplings, magnetostriction strain, polycrystals.

1 Introduction

The prediction of the magnetic behaviour of ferromagnetic materials, even in the isotropic case is still an active field of research (Bozorth, 1951; Jiles, 1991; A. Hubert et al., 1998). Another open issue is the prediction of the strain induced by magnetisation, called magnetostriction, which is closely linked to the magnetisation process, and to the magnetic domains structure. The mechanisms involved in this process can be naturally written at the magnetic domain scale - that is lower than the grain size - whereas the scale of interest for electrical engineering - the machine scale - is nearest to the centimeter scale. The object of this paper is to propose a multi-scale approach that could link these two different scales, providing a macroscopic magneto-elastic model with a strong physical content.

After an illustration of some magneto-elastic effects, a brief description of the magnetisation process is given. A micromagnetic model for single crystals, proposed by Buiron et al. (1999, 2001) is presented as well as its extension to polycrystalline media. The results are then compared to experimental data and discussed.

2 Magneto-elastic couplings

Magnetic and mechanical behaviours are coupled. It means that the magnetic behaviour cannot be accurately determined unless the mechanical fields are taken into account, and, on the other hand, the deformation state is depending on the magnetic configuration. This coupling has two main consequences.

2.1 Stress effect on magnetisation

In the case of Nickel, a compressive stress of 70 MPa doubles the initial permeability while the same amount of tensile stress reduces it about one tenth of the zero stress value. On the contrary, for materials like 68-permalloy (68% Ni-Fe alloy), the effect of stress is just the opposite. The magnetic behaviour of polycristalline iron under stress is much more complicated. At low magnetic fields, tension raises the M-H curve whereas it lowers it for higher magnetic fields (Villari effect - see for example Cullity (1972)).

2.2 Magnetostriction strain

Magnetostriction is the deformation that spontaneously occurs in ferromagnetic materials when an external magnetic field is applied. This coupling effect can be used to build magnetostrictive actuators and sensors. Magnetostriction is also partly responsible (added to magnetic forces effect) of the noise emitted by electrical devices. This strain is also very sensitive to the mechanical loading (figure 1(b)).

Moreover, this phenomenon explains several particular behaviours, such as the DE effect or the INVAR and ELINVAR effects (Bozorth, 1951).

The DE effect is an apparent loss of linearity in the elastic behaviour of demagnetised specimens. This is due to the superimposition of the magnetostriction strain to the elastic strain during the strain measurement (see figure 2). Linear behaviour is recovered when the stress is high enough to saturate magnetostriction.

INVAR and ELINVAR effects are an apparent insensitivity for specific compositions to a change in temperature. The INVAR effect is the apparent absence of thermal dilatation in a specific range of temperature, due to the superimposition of the magnetostriction strain to the thermal strain. The ELINVAR effect is the apparent constancy of the Young modulus with a change in temperature.

These complex coupling phenomena are supposed to be strongly correlated with the magnetic microstructure, and thus have to be described and modelled at the relevant scale. This point is the object of next section, where the study has been restricted to polycristalline media, and where the case of iron-based alloys is emphasized.

3 Magnetisation process at the grain scale

Each grain of a ferromagnetic polycrystalline material is divided into domains (figure 3) that are magnetised at saturation, whatever the external magnetic field (Bozorth, 1951). In each domain a, the magnetisation 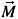_a can be written:

The magnetisation in these domains is initially oriented along the easy directions of magnetisation of the crystal. Easy directions being < 100 > for iron, six domain families a are possible. The domains structure changes while increasing the external magnetic field thanks to domain walls motion: domains whose orientation is closer to the orientation of the applied field grow while others shrink. For high values of the applied magnetic field, the magnetisation of the domains rotates towards the direction of the magnetic field. When complete magnetic saturation is reached, each grain is composed of a unique domain that is magnetised in the direction of the applied field.

4 Microscopic model

The first step of this magneto-mechanical modelisation is to get an accurate description of the single crystal behaviour, accounting for the two distinct mechanisms involved in the magnetisation process. It can be noticed that the same model can be applied for a grain embedded in a polycrystal.

4.1 Magnetostriction strain

If the magnetisation

_a is known, the magnetostriction strain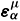 in the domain is known and can be written in the crystallographic frame CF. In the case of a cubic crystallographic symmetry, the tensor 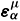is (A. Hubert et al., 1998):

where l₁₀₀ and l₁₁₁ are the magnetostrictive constants for the single crystal, l₁₀₀ (resp. l₁₁₁) being the strain measured in the direction parallel to the < 100 > (resp. < 111 > ) axis of a single crystal, when it is magnetised at saturation along this axis.

Relation (2) can be written in the following condensed form:

defining:

with¹:

4.2 Mechanical behaviour

Considering the low level of stresses that will be considered hereafter, the mechanical behaviour of a single crystal is written in the framework of linear elasticity, with an usual Hooke law:

where s_g and denote the stress and the elastic strain tensors in the single crystal whereas 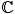^I is the stiffness tensor for the single crystal, assumed to be magnetic field independent.

4.3 Magnetic behaviour

We use here after the description of the magneto-elastic behaviour of single crystals proposed by Buiron et al. (1999, 2001). This approach is derived from Néel magnetic phase model (Néel, 1944).

4.3.1 Magnetic state variables

The state variables chosen to describe the magnetisation of a single crystal are divided in two distinct sets. For each domain family a, we define:

• The disorientation angle q_a being the angle between the crystallographic easy direction of the a domain family and the present direction of its magnetisation _a. We assume here that _a is always in the plane formed by the easy direction and the magnetic field.

• The volumetric fraction f_a of the a domain family in the single crystal.

4.3.2 Potential energy of a domain

In order to determine the state variables, we write the potential energy at the magnetic domain scale, considering three major contributions:

• is the magnetostatic energy, tending to create a magnetisation parallel to the magnetic field. It can be written:

where

_g denotes the mean magnetic field in the crystal and _a the magnetisation in the a domain: _a = M_s = M_s^t[g₁,g₂,g₃].

• is the anisotropy energy tending to prevent, in each domain, the rotation of the magnetisation from the easy axes. In the case of cubic crystallographic structure:

where K₁ and K₂ denote the anisotropy constants for the single crystal.

If we note:

the anisotropy energy can be written:

• is the magneto-elastic energy describing the couplings effects between the magnetisation and the local stress s_g (mean value within the single crystal):

where is the magnetostriction strain tensor in the a domain, defined by equation (3).

Using the previous notations, the total potential energy of a domain is defined by equation (13):

This expression does not account for the exchange energy and for the pure elastic energy. The elastic energy is assumed to be constant over a grain, and thus does not participate to the equilibrium of a single crystal. On the other hand, the variations of the exchange energy near the domains border is accounted for thanks to the parameter A_s presented here after (Buiron, 2000).

4.3.3 State variables calculation

• The q_a variables are obtained after minimisation of the potential energy of each domain family:

If

₀ is the initial easy axis for the domain a, q_max is defined by:

• The f_a variables are obtained using the explicit relation proposed by Buiron et al. (2001):

where A_s is an adjustment parameter, accounting for the non uniformity of the exchange energy, the magnetic field and the stress tensor within the single crystal.

4.3.4 Definition of the single crystal behaviour

Once the state variables are known for each domain family a, we can define the magnetisation as the mean magnetisation over the crystal:

We can also define the mean magnetostriction strain in the single crystal:

4.4 Results

Experimental measurements are available in the litterature for pure iron single crystal² (Webster, 1925). The material constants used are as follows:

Figure 4 shows a very good agreement between experimental and numerical results, both concerning the magnetisation and the magnetostriction.

5 Multiscale model

In the case of polycrystalline media, the strain, the stress, the magnetisation and the magnetic field are not homogeneous within the material. The local behaviour (at the grain scale) has to be written with respect to the local loading. This local loading can be, with specific assumptions concerning the microstructure, deduced from the macroscopic loading.

5.1 Multiscale approach - principle

We work on a Representative Volume Element (RVE) of a polycrystalline ferromagnetic material. Its texture is known through an Orientation Data File obtained after an EBSD (or X-ray) measurement. The single crystal properties (detailed in equation (19)) are known.

The objective is to link the macroscopic response (mean magnetisation

_M and strain E) of this RVE to the macroscopic loading (the external field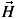 _ext and the macroscopic stress S).

The general idea of this micro-macro approach (see figure 5) is to postulate a localisation law, in order to calculate the local loading. The micro-model is then applied at the domains scale and the macro-level is reached through an averaging operation. Since both the local values for the stress and the magnetic field depend on the local magnetisation and strain, an iterative process has to be used.

Each step of this calculation is described here after.

5.2 Localisation step

5.2.1 Elastic behaviour

The aim of this step consists in deriving the local stress from the external loading, postulating a particular form for the function g in relation (20).

The function g is here deduced from a self-consistent approach. Each grain is considered as an inclusion in the homogeneous medium equivalent to the polycrystal, so that the problem can be linked to the solution of the Eshelby inclusion problem (Esheby, 1957).

The magnetostriction strain is considered as a free strain. The Eshelby tensor ^E is calculated³ following Mura (1982). ^E links the free strain () in a region (the inclusion) of the infinite media to the total strain e^I in this region:

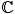From the Eshelby solution, we can deduce, through a self-consistent scheme, the stiffness tensor of the homogeneous medium equivalent to the polycrystal. Details of this approach are given in ^{appendix A}. Each grain (of stiffness ^I) is considered as an inclusion in this equivalent homogeneous medium. The equivalent stiffness tensor 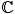^eff is solution of the implicit equation (22):

where the symbol < . > denotes an averaging operation over the volume and 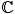* denotes the Hill constraint tensor.

We can also define the two 4^th order localisation operators (see details in ^{appendix A}):

• the strain localisation tensor :

• the stress concentration tensor :

This scheme is used to express the relation (20). The local stress is written as the sum of two terms (equation (25)).

The first one depends on the macroscopic stress tensor S and on the stress concentration law. The second term is linked to the elastic incompatibility strain due to the existence of a free strain in the grain, and to the stiffness of the surrounding medium. In the case of iron-silicon alloys, the magnetostriction magnitude - that do not exceed 10^-5 - justify the fact that the incompatibility stresses involved remain in the elastic domain.

It must be noticed that this relation is an implicit relation, since is a function of s_g.

5.2.2 Magnetic behaviour

The aim of this step consists in deriving the local magnetic field from the external loading, postulating a given form for the function h in relation (26).

This equation is usually written (in electrotechnical engineering) in the form of relation (27).

where the local perturbation of the macroscopic magnetic field is taken into account through the demagnetising field

_d. The general form of the localisation law can be written:

with

_M the mean magnetisation in the material,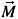 _g the local magnetisation. K is a 2^nd order operator, depending on the magnetisation, on the stress state, and on the shape choosen for the inclusion.

In the case of stress independent linear isotropic magnetic behaviour, and spherical inclusions, the tensor K can be replaced by a scalar value N_c (see ^{appendix B}).

Herein, as a first approximation, we choose to extend this relation to anisotropic non-linear magnetic behaviour. We keep the form of equation (28), and use a particular value for N_c. It could also be possible to use a variable value of N_c computed from the value of c_M recalculated at each step of the iterative scheme.

5.3 Local behaviour

The grain behaviour model has been described in paragraph 4. From the local loading s_g and 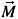_g, we can obtain in each grain the magnetisation 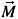_g and the total strain e_g (e_g = + 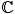^I-1 : s_g).

5.4 Homogenisation

The last step in the micro-macro modelisation is the homogenisation step to get back to the macro-scale. We define:

As the scheme is self-consistent, an iterative procedure has to be built up. The calculation is then done until convergence.

6 Results and comparison to experimental data

Computations have been made using a 500 grains RVE of an industrial alloy. This commercial iron-silicon alloy indicates no morphologic texture (figure 6(a)). The mean grain size is about 70 mm. The texture is known thanks to EBSD measurements (figure 6(b)).

Sample for all experiments consists of 250 mm long and 12.5 mm wide bands cut by electro-erosion machining (in order to avoid residual stresses that have a strong influence on the magneto-mechanical behaviour). The specimens are cut every 10^° from the rolling direction (RD).

6.1 Macroscopic elastic behaviour

Tensile tests have been carried out to measure the Young's modulus and the Poisson's ratio thanks to standard strain gauges measurements. Young's modulus and Poisson's ratio evolution in the sheet plane are plotted in figure 7(a) and 7(b). A good agreement between experimental and numerical data is shown. Calculations using the Reuss and Voigt extremal hypotheses are also plotted.

Other methods for estimating the elastic moduli of a textured polycristal, such as the Hashin and Shtrickman bounds, or finite elements methods with periodic boundary conditions are presented in Daniel (2003). These methods give estimates between the Voigt and Reuss bounds (for which no specific assumption is made concerning the phases distribution). The particular variation with q, linked to the combination of the single crystal anisotropy with the texture data, is similar for all these estimates.

6.2 Macroscopic magnetic behaviour

Two kinds of calculations have been made concerning the magnetic uncoupled behaviour: firstly without considering any demagnetising field (homogeneous magnetic field hypotheses: N_c = 0, 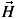_g = 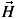_ext), and secondly introducing a demagnetising field calculation (N_c = 5.10^-4).

It must be noticed that the resolution of the implicit equation (28) leads, in the case of non-linear behaviour to numerical difficulties: the computational costs are high, and the convergence depends on the quality of the initial solution in the general algorithm (see figure 5): an appropriate choice of this initial solution enables to avoid dissuasive computation times.

Magnetic measurements were obtained using a non-standard experimental frame (Hubert et al., 2002). The results are plotted on figure 8(b).

The demagnetising field introduction tends to decrease the magnetic permeability (figure 8(a)). The effect is inexistant for very high or very low values of the external field - for which the macroscopic behaviour is almost linear and the local magnetic field heterogeneity low -, but very strong in the saturation knee area, where a high level of magnetic field heterogeneity is highlighted (figure 9).

Comparison with experimental data (figure 8(b)) shows a good qualitative agreement, although the predicted magnetisation is over-estimated.

6.3 Macroscopic magnetostrictive behaviour

The same experimental procedure, with strain gauges, is used to measure magnetic strains. These mesurements are corrected to deduct the so-called form-effect (Billardon et al., 1995; Daniel et al., 2003) and obtain the true magnetostriction strain. Experimental and numerical results are plotted on figure 10.

The demagnetising field calculation tends to weakly reduce the magnetostriction amplitude (figure 10(a)). The predicted general level is correct compared to experimental measurements (figure 10(b)), but the relative anisotropy between the rolling and the transverse directions is not respected. This problem is the object of a work in progress (Daniel et al., 2003); this point is related to the initial state of the specimens, and particularly residual stresses and surface effects, that can explain this disagreement beetween calculation and experimental observations (Daniel, 2003).

7 Conclusion

A 3-dimensional physically based magneto-elastic model has been presented. It provides accurate results for single crystal behaviour, and a good description of magnetic and elastic uncoupled behaviours of ferromagnetic polycrystalline materials. The level of magnetostriction can also be predicted.

Several works are presently in progress to improve this micro-macro approach.

A first way is to refine the magnetic localisation law, for example introducing a magnetic field dependency for K in equation (28).

Another direction would be to get a more precise description and understanding of the domains microstructure. This description is presently limited to the volumetric fraction f_a and the disorientation angle q_a for each domain family.

This kind of micro-macro strategy could then participate in the understanding of the effect of stress on the magnetic behaviour, especially in the case of multi-axial loadings.

Received: 15/IV/03. Accepted: 02/X/04.

#575/03.

Consider an unloaded homogeneous infinite medium of moduli

^o. A region I of this medium (the inclusion) is submitted to a free strain e^L. This strain is the strain that would act in the inclusion if no resistance was exerted by the surrounding medium. The actual strain e^I in the inclusion can be linked to the free strain using the Eshelby tensor (Esheby, 1957):

The fourth order tensor

^E only depends on the elastic moduli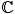 ^o and on the shape chosen for the inclusion. Elements concerning the calculation of this tensor can be found in Mura (1982). The stress in the inclusion is linked to the elastic strain by the Hooke relation:

It can be shown (Bornert et al., 2001) that the problem of an elastic heterogeneity (that is the case considered for polycrystals) can be reduced to an inclusion problem. A fictive equivalent free strain e^L* is defined, that would lead to the same strain and stress state in the inclusion than the one acting in the heterogeneity. The macroscopic loading is defined by the macroscopic stress S, and the macroscopic strain is E. Stress and strain in the inclusion are defined by relations (33) and (34)

that can be written:

Introducing this relation in equation (33), one obtains:

^* being the Hill constraint tensor defined by relation (37):

If we now come back to the problem of the elastic heterogeneity (the strain being purely elastic), the behaviour law is:

and at the macroscopic scale:

From equation (36), it comes:

that leads to:

that can also be written using equation (38):

The strain localisation tensor is derived from equation (41):

This fourth order operator links the macroscopic strain to the local strain in the inclusion:

The stress concentration tensor is derived from equation (38), (39) and (44):

This fourth order operator links the macroscopic stress to the local stress in the inclusion:

The definitions of 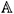and 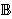are given in the paper as equation (23) and (24).

The macroscopic stress is linked to the local stresses through relation (47) (equation (42) is used):

This leads to a relationship that must be verified by the effective moduli tensor

^eff, noted equation (22) in the paper:

Relations (28) and (29) defining the localisation law for the magnetic field are derived from the solution of a magnetostatic problem for an inclusion.

The behaviour law for the spherical region (of radius R) is written:

The behaviour law for the infinite medium is written:

Without any current density, the Maxwell equations can be written:

Under these conditions, the magnetic field can be derived from a scalar potential:

Applying the isotropic behaviour law ( = m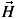) leads to the Poisson equation for the potential:

The solutions for the potential j can be written:

H_¥ being the value for the magnetic field very far from the inclusion. The magnetic field can then be written, following equation (52):

- inside the sphere:

- outside the sphere:

The boundary conditions at the interface of the inclusion give ( is the unit vector normal to the sphere surface):

a) for q = and r = R:

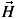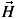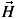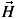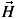where the symbol [] denotes the jump of through the surface ([] = _ext - _int).

From equation (57) we can deduce:

b) for q = 0 and r = R:

Replacing the value of k in equation (59) leads to:

that can also be written:

finally leading to the expression:

As both magnetisation and magnetic fields appearing in equation (62) are parallel to the direction 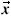, this relation can be written in a vectorial way:

This relation justify the choice made for relation (28), and the particular value of N_c in equation (29).

• [1] Billardon R. and Hirsinger L., J. Mag. Mag. Mat., 140-144 (1995), 2199.
• [2] Bornert M., Bretheau T. and Gilormini P., Homogénéisation en mécanique des matériaux. Tome 1: Matériaux aléatoires élastiques et milieux périodiques, Hermès Science Paris (2001).
• [3] Bozorth R.M., Ferromagnetism, Van Nostrand New York (1951).
• [4] Buiron N., Modélisation multi-échelle du comportement magnéto-élastique couplé des matériaux ferromagnétiques doux, Thčse de doctorat, Ecole Normale Supérieure de Cachan, France (2000).
• [5] Buiron N., Hirsinger L. and Billardon R., J. Phys. IV, 9 (1999), 187-196.
• [6] Buiron N., Hirsinger L. and Billardon R., J. Phys. IV, 11 (2001), 373-380.
• [7] Cullity B.D., Introduction to magnetic materials, Addison-Wesley (1972).
• [8] Daniel L., Modélisation multi-échelle du comportement magnéto-mécanique des matériaux ferromagnétiques texturés, Thčse de doctorat, Ecole Normale Supérieure de Cachan, France (2003).
• [9] Daniel L., Hubert O., Ossart F. and Billardon R., J. Phys. IV, 105 (2003), 247-253.
• [10] Eshelby J.D., Proc. R. Soc. Lond., A421 (1957), 376.
• [11] Hubert A. and Schäfer R., Magnetic domains, Springer (1998).
• [12] Hubert O., Influence des contraintes internes et de la structure des dislocations sur les couplages magnéto-mécaniques dans les alliages Fe-3%Si ŕ grains non orientés, Thčse de doctorat, Université Technologique de Compičgne, France (1998).
• [13] Hubert O., Daniel L. and Billardon R., J. Mag. Mag. Mat., 254-255C (2002), 352-354.
• [14] Jiles D.C., Introduction to Magnetism and Magnetic Materials, Chapman and Hall (1991).
• [15] McClintock F.A. and Argon A.S., Mechanical behavior of materials, Addison-Wesley Publishing Company (1966).
• [16] Mura T., Micromechanics of defects in solids Martinus Nijhoff Publishers (1982).
• [17] Néel L., J. Phys. Radiat., 5 (1944), 241.
• [18] Webster W.L., Proc. Roy. Soc., 109A (1925), 570.

Appendix A:  Determination of the stress and strain localisation tensors

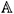and the stress concentration tensor 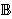are derived from the solution of the Eshelby's inclusion problem (Esheby, 1957). Their definition is for example extensively defined in Bornert et al. (2001) and summarized hereafter.

Appendix B:  Determination of the magnetic field localisation operator

.

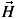
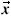We consider a spherical isotropic magnetic region embedded in an infinite isotropic magnetic medium. This medium is submitted to an uniform (at the boundary) magnetic field

_¥ = H_¥.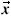

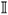1

d

_ij is the Krönecker symbol and

the identity fourth order tensor.

2

For which the crystallographic symmetry is cubic.

3

For the applications considered in this paper inclusions are taken spherical, assuming an isotropic distribution of the grains.

Publication Dates

• Publication in this collection
  11 July 2005
• Date of issue
  Dec 2004

History

• Accepted
  02 Oct 2004
• Received
  15 Apr 2003