Some remarks on the stability and boundedness of solutions of certain differential equations of fourth-order

Abstract

There are given sufficient conditions for the asymptotic stability of the zero solution of equation (1.1) with p = 0 and the boundedness of all solutions of the same equation (1.1), with p <FONT FACE=Symbol>¹</FONT> 0.

differential equations of fourth order; stability; boundedness; Lyapunov function

Some remarks on the stability and boundedness of solutions of certain differential equations of fourth-order

Cemil Tunç

Department of Mathematics, Faculty of Arts and Sciences Yüzüncü Y1l University, 65080, Van, Turkey, E-mail: [e-mail]

ABSTRACT

There are given sufficient conditions for the asymptotic stability of the zero solution of equation (1.1) with p = 0 and the boundedness of all solutions of the same equation (1.1), with p ¹ 0.

Mathematical subject classification: 34D20, 34D99.

Key words: differential equations of fourth order, stability, boundedness, Lyapunov function.

1 Introduction

The equation studied here is of the form

where j, f, g, h and p are continuous functions which depend only on the arguments displayed. The dots indicate differentiation with respect to the independent variable t and all solutions considered are assumed real. The derivatives,

exist and are continuous. Moreover, the existence and the uniqueness of the solutions of the equation (1.1) will be assumed.

Ever since Lyapunov [20] proposed his famous direct (or second) method on the stability of motion, numerous methods have been proposed in the relevant literature to derive suitable Lyapunov functions and hereby, in particular, many papers and books have been devoted to the study of stability and boundedness of solutions of certain second-, third-, fourth-, fifth- and sixth order nonlinear differential equations (see, for example, Anderson [1], Barbasin [3], Cartwright [4], Chin ([5], [6]), Ezeilo ([8], [9]), Harrow ([10], [11]), Ku and Puri [13], Ku et al. [14], Ku ([15], [16]), Krasovskii [17], Leighton [18], Li [19], Marinosson [21], Miyagi and Taniguchi [22], Ogundare [23], Ponzo [24], Quian [25], Reissig et al. [26], Schwartz and Yan [27], Shi-zong et al. [28], Sinha ([29], [30]), Skidmore [31], Szegö [32], Tejumola ([33], [34]), Tiryaki and Tunç [35], Tunç ([36], [37], [38], [39], [40], [41], [42], [43]), Zubov [44], Wu and Xiong [45] and references quoted therein for some publications on these topics). So far, perhaps, the most efficient tool for the study of the stability and boundedness of solutions of a given nonlinear differential equation is provided by Lyapunov theory. This theory is based on the use of positive definite functions that are non-increasing along the solutions of differential equations under consideration. But, finding an appropriate Lyapunov function is in general a difficult task. Despite having derived Lyapunov functions for special cases of equation (1.1), Chin [6] remarks that ''it is difficult to derive suitable Lyapunov functions for the differential equations of the fourth-order''. It also worth mentioning the following opinions of some authors about the method: Iggidr and Sallet [12] express that ''The most efficient tool for the study of the stability of a given non-linear system is provided by Lyapunov theory''. Further, in [25], Qian says that ''So far, the most effective method to study the stability of nonlinear differential equations is still the Lyapunov's direct method''. For some related papers on the construction of Lyapunov's functions, one can refer to the works summarized by Chin [5] about the subject and the references cited therein. In [6], Chin has tried to use a new technique (the intrinsic method) proposed by himself to construct new Lyapunov functions for the following fourth-order non linear differential equations

and

so that they are far less restrictive than those presented in some literature. Later, the authors in [35] based on the results in [6] have extended the method used in [6] to construct new Lyapunov functions to investigate the stability of the zero solution x = 0 of non-linear differential equations described by

x⁽⁴⁾ + a₁ + f(x, ) + a₃ + h(x) = 0

and

x⁽⁴⁾ + a₁ + f(x, ) + g() + a₄x = 0

But, in 1998, Wu and Xiong [45] proved that the Lyapunov functions constructed by Chin [6] were the same as those obtained by Cartwright [4] and Ku [15],and Chin's results [6] were not true for the equations (1.2), (1.3), and (1.4) in the general cases. The local asymptotic stability of zero solution of the equations (1.2), (1.3) and (1.4) has also been discussed by Wu and Xiong [45]. Therefore, in this paper, the results obtained in [35] will be revised and improved, and some additional results to be obtained for the non-linear differential equations of the form (1.1) will be given. Equation (1.1) can be written in the phase variables form as

It should also be noted that the domain of attraction of the zero solution x = 0 of equation (1.1) (for p º 0) in the following first result is not going to be determined here.

2 Stability and boundedness results

Set

In the case p º 0, we establish the following result.

Theorem 1. Assume that

(i) h(0) = g(x, 0) = 0,

(ii) there are constants a > 0, b > 0, c > 0, d > 0, d > 0 and e > 0 such that

abc – cg_y(x, y) – adj(z) > d > 0 for all x, y and z

in which e < , D = ab + ,

(iii) 0 < d - h^¢(x) < for all x and h(x)sgnx ® + ¥, as |x| ® ¥,

(iv) 0 < g₁(x, y) - c < for all x and y ¹ 0, and - < yg_x(x, y) < 0 for all x and y,

(v) 0 < - b < minfor all x, y and z ¹ 0, and yf_x(x, y, z) < 0 for all x, y and z

(vi) j(z) > a, j₁(z) - j(z) < for all z.

Then the zero solution of system (1.5) is asymptotically stable.

Remark 1. Making the use of condition (ii) of Theorem 1, we can obtain

j(z) < , g_y(x, y) < ab.

Remark 2. If we take j() = a, f(x, , ) = b, g(x, ) = c, h(x) = dx instead of equation (1.1), then equation (1.1) reduces to the linear constant coefficient differential equation and conditions (i)-(vi) of Theorem 1 reduce to the corresponding Routh-Hurwitz criterion.

Remark 3. Theorem 1 revises the first theorem in [35] and includes and improves the results of Ezeilo ([8], [9]), Harrow [10], Tunç [42, Theorem 2.1] and Wu and Xiong [45] except of the restriction on the function f, that is

0 < – b < min

Throughout our main results, we use as a basic tool the scalar Lyapunov function V = V(x,y,z,w) defined by:

where

The following lemmas will be needed in the proof of Theorem 1 and forthcoming results.

Lemma 1. Assume that all the conditions of Theorem 1 be satisfied. Then there are positive constants D_i º D_i(a, b, c, d, e, d), (i = 1, 2, 3, 4) such that

V>D₁

h(x) dx + D₂y² + D₃z² + D₄w²

for all x, y, z and w.

Proof. Since > c, it follows that

2

g(x, h)dh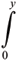 = 2 hdh > cy².

Therefore, the Lyapunov function 2V in (2.1) can be rearranged as:

In view of the assumptions of Theorem 1, the values of a, b in (2.2) and the mean value theorems (both for the derivative and integral) it can easily be concluded that

2V > e h(x)dx + y² + z² + ew².

This completes the proof of Lemma 1.

Lemma 2. Assume that all the conditions of Theorem 1 be satisfied. Then there exist positive constants D_i º D_i(a, b, c, e, d) (i = 5, 6, 7) such that whenever (x(t), y(t), z(t), w(t)) is any solution of system (1.5), then

Proof. Along any solution (x, y, z, w) of system (1.5) it follows from (2.1) and (1.5) that

Subject to conditions (ii)-(vi) of Theorem 1 and (2.2) we have that

where

In view of the inequalities

respectively, and the assumptions of Theorem 1, we have that

By collecting the estimates (2.5)-(2.8) into (2.4) we obtain

which proves the lemma.

Proof of Theorem 1. Taking into consideration Lemma 1, Lemma 2 and condition (iii) of Theorem 1, it follows that

V(x, y, z, w) = 0 if and if only x² + y² + z² + w² = 0,

V(x, y, z, w) > 0 if and if only x² + y² + z² + w² > 0,

V(x, y, z, w) ® ¥ 0 if and if only x² + y² + z² + w²® ¥.

Let g denote a trajectory (x(t), y(t), z(t), w(t)) of the system (1.5) with p(t, x, y, z, w) º 0 such that t = 0, x = x₀, y = y₀, z = z₀, w = w₀, where (x₀, y₀, z₀, w₀) is an arbitrary point in x, y, z, w-space from which motions may originate. Then by Lemma 2 for t > 0, it clear that

V(x, y, z, w) = V(x(t), y(t), z(t), w(t)) = V(t) <V(0).

Moreover, V(t) is non-negative and non-increasing and therefore tends to a nonnegative limit, V(¥) say, as t ® ¥. Suppose V(¥) > 0. Consider the set

S{(x, y, z, w) | V(x, y, z, w) <V(x₀, y₀, z₀, w₀)}.

Because of the properties of the function V in (2.1) we know that S is bounded, and therefore the set g Ì S is also bounded. Further, the nonempty set of all limit points of g consists of whole trajectories of the system

lying on the surface V(x, y, z, w) = V(¥). Thus if P is a limit point of g, then there exists a half-trajectory, say g_P of the above system, issuing from P and lying on the surface V(x, y, z, w) = V(¥). Since for every point (x, y, z, w) on g_P we have V(x, y, z, w) > V(¥), this implies that \overset.V = 0 on g_P. Also, in view of the inequality obtained in Lemma 2, that is

= 0 implies y = z = w = 0; and by the above system, assumptions (i), (iii) of Theorem 1 this means that x = 0. Thus, the point (0, 0, 0, 0) lies on the surface V(x, y, z, w) = V(¥) and hence V(¥) = 0.

This completes the proof of Theorem 1.

In the case p ¹ 0 we have the following result.

Theorem 2. Assume that

(i) g(x, 0) = 0,

(ii) conditions (ii)-(vi) of Theorem 1 hold,

(iii) | p(t, x, y, z, w)| < (A + |y| + |z| + |w|)q (t), where q(t) is a non-negative and continuous function of t, and satisfies

q(s)ds < B < ¥ for all t > 0,

A and B are positive constants. Then for any given finite constants x₀, y₀, z₀ and w₀, there exists a constant K = K(x₀,y₀,z₀,w₀), such that any solution (x(t) ,y(t), z(t), w(t)) of system (1.5) satisfying the initial condition

x(0) = x₀, y(0) = y₀, z(0) = z₀, w(0) = w₀

satisfies for all t> 0,

|x(t)| < K, |y(t)| < K, |z(t)| < K, |w(t)| < K.

Remark 4. Theorem 2 revises and improves the second result obtained in [35], and generalizes the results of Ezeilo [8], Harrow [11] and Tunç [42, Theorem 2.7].

Proof of Theorem 2. The proof of this theorem is based essentially on the method devised by Antosiewicz [2]. Now, let (x(t), y(t), z(t), w(t)) be an arbitrary solution of the system (1.5) satisfying the initial conditions

x(0) = x₀, y(0) = y₀, z(0) = z₀, w(0) = w₀

given in Theorem 2. Next, consider the Lyapunov function V(t) = V(x(t), y(t), z(t), w(t)), where V is defined by (2.1). Because of h(0) is not necessarily zero now; we have only the following estimate in the proof of theorem

and since p ¹ 0, the conclusion of Lemma 2 can be revised as follows

< – (D₅y² + D₆z² + D₇w²) + (aw + z + by) p(t, x, y, z, w).

Let D₈ = max(a, 1, b). Then, we have

< – D₈ (|y| + |z| +|w|) (A + |y| + |z| +|w|) q(t).

Making the use of the inequalities

|w| < 1 + w² and |2yz| < y² + z²

we obtain

where D₉ = D₈(A + 1). It follows from (2.9) that

D₁₀ = min(D₂, D₃, D₄) and D₀ = () h²(0). Now, combining expressions (2.10) and (2.11) we get

where D₁₁ = D₉(3 + ), D₁₂ = . Integrating expression (2.12) between 0 to t, we obtain

V(t) – V(0) < D₁₁

q(s)ds + D₁₂

V(s)q (s)ds.

Setting D₁₃ = D₁₁B + V(0), and using condition (iii) of Theorem 2 we have

V(t) <D₁₃ + D₁₂

V(s)q (s)ds.

Hence, Gronwall-Bellman inequality yields

V(t) <D₁₃ exp D₁₂

q(s)ds.

The proof of Theorem 2 is now complete.

If p is a bounded function, then the constant K above can be fixed independent of x₀, y₀, z₀ and w₀, as will be seen from our next result.

Theorem 3. Assume that g(x, 0) = 0 and conditions (ii)-(vi) of Theorem 1 hold, and that p(t, x, y, z, w) satisfies

|p(t, x, y, z, w)| < D < ¥

for all values of t, x, y, z and w, where D is a positive constant. Then there exists a constant K₁whose magnitude depends a, b, c, d, d, e as well as on the functions j, f, g and h such that every solution (x(t), y(t), z(t), w(t)) of system (1.5) ultimately satisfies

|x(t)| < K₁, |y(t)| < K₁, |z(t)| < K₁, |w(t)| < K₁.

Remark 5. Note that in [34], Tejumola extended the boundedness results given in [33] to a special case of equation (1.1). Theorem 3 is also another extension of [33]. Theorem 3 extends the results of Tunç [42, Theorem 2.9] and improves the results of Wu and Xiong [45] except of the restriction on the function f, that is,

0 < – b < min .

Now, the actual proof of Theorem 3 will rest mainly on certain properties of a piecewise continuously differentiable function V₁ = V₁(x, y, z, w) defined by V₁ = V + V₀, where V is the function given by (2.1) and V₀ is defined as follows:

The first property of V₁ is stated in the following.

Lemma 3. Subject to the conditions of Theorem 3, there is a constant D₁₄ such that

and

Proof. From (2.13) we have |V₀(x, w)| < |w| for all x and w. Hence

V₀(x, w) > – |w| for all x and w.

By combining the estimates obtained for V and V₀ we get the estimate for V₁

By using condition (iii) of Theorem 1 we deduce that the integral on the right-hand here is non-negative and tends to infinity when x do so. It is evident that (2.14) and (2.15) are verified, where D₁₄ = which completes the proof of Lemma 3.

The next property of the function V₁ is connected with its total time derivative and is contained in the following lemma.

Lemma 4. Let (x, y, z, w) be any solution of the differential system (1.5) and the function v₁ = v₁(t) be defined by v₁(t) = V₁(x(t), y(t), z(t), w(t)). Then the limit

exists and there is a constant D₁₅ such that

(t) < – 1 provided x²(t) + y²(t) + z²(t) + w²(t) > D₁₅.

Proof. In accordance with the representation V₁ = V + V₀ we have a representation v₁ = v + v₀. The existence of is quite immediate, since v has continuous first partial derivatives and v₀ is easily shown to be locally Lipschitizian in x and w so that the composite function v₁ = v + v₀ is at the least locally Lipschitizian in x, y, z and w. Taking into consideration to the assumptions of Theorem 3 an easy calculation from (2.13) and (1.5) shows that

where

By noting the estimates obtained for and , we see that

or

Then by an argument similar to that in the proof of the theorem in Ezeilo [8], one may show that the inequality in Lemma 4 can be easily obtained. Hence the details of the proof are omitted. The proof of this lemma is now complete.

Proof of Theorem 3. Throughout Lemma 3 and Lemma 4, we have proved that the function V₁ = V + V₀ has the following properties:

and

< –1 provided x² + y² + z² + w² + D¹⁵.

Applying the usual Yoshizawa-type argument, Theorem 1 in Chukwu [7], to the above expressions we can conclude for any solution (x(t), y(t), z(t), w(t)) of the system (1.5) that

|x(t)| < K₁, |y(t)| < |z(t)| < K₁, |w(t)| < K₁

for sufficiently large t.

Thus the proof of Theorem 3 is complete.

Acknowledgement. The author would like to express sincere thanks to the anonymous referees for their invaluable corrections, comments and suggestions.

Received: 10/VII/06. Accepted: 03/I/07.

#674/06.

• [1] L.R. Anderson and W. Leighton, Liapunov functions for autonomous systems of second order. J. Math. Anal. Appl., 23 (1968), 645-664.
• [2] H.A. Antosiewicz, On non-linear differential equations of the second order with integrable forcing term. J. London Math. Soc., 30 (1955), 64-67.
• [3] E.A. Barbashin, The construction of Liapunov function (Russian). Differ. Uravn, 4 (1968), 2127-2158.
• [4] M.L. Cartwright, On the stability of solutions of certain differential equations of the fourth-order. Quart. J. Mech. and Appl. Math., 9(4) (1956), 185-194
• [5] P.S.M. Chin, Generalized integral method to derive Lyapunov functions for nonlinear systems. Internat. J. Control., 46(3) (1987), 933-943.
• [6] P.S.M. Chin, Stability results for the solutions of certain fourth-order autonomous differential equations. Internat. J. Control., 49(4) (1989), 1163-1173.
• [7] E.N. Chukwu, On the boundedness of solutions of third order differential equations. Ann. Mat. Pura Appl., 104(4) (1975), 123-149.
• [8] J.O.C. Ezeilo, On the boundedness and the stability of solutions of some differential equations of the fourth order. J. Math. Anal. Appl., 5 (1962), 136-146.
• [9] J.O.C. Ezeilo, A stability result for solutions of a certain fourth order differential equation. J. London Math. Soc., 37 (1962), 28-32.
• [10] M. Harrow, A stability result for solutions of certain fourth order homogeneous differential equations. J. London Math. Soc., 42 (1967), 51-56.
• [11] M. Harrow, On the boundedness and the stability of solutions of some differential equations of the fourth order. SIAM. J. Math. Anal., 1 (1970), 27-32.
• [12] A. Iggidr and G. Sallet, On the stability of non-autonomous systems, Automatica J. IFAC, 39(1) (2003), 167-171.
• [13] Y.H. Ku and N.N. Puri, On Liapunov functions of high order nonlinear systems. J. Franklin Inst., 276 (1963), 349-364.
• [14] Y.H. Ku, R. Mekel and C. Su, Stability and design of nonlinear control systems via Liapunov's criterion. IEEE Internat. Convention Record (1964), 154-170.
• [15] Y.H. Ku, Lyapunov function of a fourth-order system. IEEE Transactions Automatic Control, 9 (1964), 276-278.
• [16] Y.H. Ku, Lyapunov function of a sixth-order nonlinear system. Proc. IEEE, 57 (1969), 91-94.
• [17] N.N. Krasovskii, On the stability in the large of the solution of a nonlinear system of differential equations (Russian). Prikl. Mat. Meh., 18 (1954), 735-737.
• [18] W. Leighton, On the construction of Liapunov functions for certain autonomous nonlinear differential equations. Contributions to Differential Equations, 2 (1963), 367-383.
• [19] Q. Li, On the construction of globally asymptotically stable Liapunov's functions of a type of nonlinear third-order systems. Ann. Differential Equations, 7(1) (1991), 39-51.
• [20] A.M. Lyapunov, Stability of Motion, Academic Press, London, 1966, p. 203.
• [21] S.F. Marinosson, Lyapunov function construction for ordinary differential equations with linear programming. Dyn. Syst., 17(2) (2002), 137-150.
• [22] H. Miyagi and T. Taniguchi, Application of the Lagrange-Charpit method to analyse the power system's stability. Internat. J. Control, 32(2) (1980), 371-379.
• [23] B.S. Ogundare, Boundedness of solutions to fourth order differential equations with oscillatory restoring and forcing terms. Electron. J. Differential Equations, 2006(6) (2006), 1-6.
• [24] P.J. Ponzo, On the stability of certain nonlinear differential equations. IEEE Trans. Automatic Control, 10 (1965), 470-472.
• [25] C. Qian, On global stability of third-order nonlinear differential equations. Nonlinear Anal., 42(4) (2000), Ser. A: Theory Methods, 651-661.
• [26] R. Reissig, G. Sansone and R. Conti, Non-linear Differential Equations of Higher Order. Translated from the German. Noordhoff International Publishing, Leyden, 1974, 669 pp.
• [27] C.A. Schwartz and A. Yan, Construction of Lyapunov functions for nonlinear systems using normal forms. J. Math. Anal. Appl., 216(2) (1997), 521-535.
• [28] L. Shi-zhong, L. Zheng-rong and Y. Yuan-hong, Stability for certain fourth-order nonlinear differential equations, Demonstratio Mathematica, 31(1) (1998), 87-96.
• [29] A.S.C. Sinha, Stability result of a sixth order non-linear system. Automatica J. IFAC, 7 (1971), 641-643.
• [30] A.S.C. Sinha, On stability of sixth-order nonlinear system. Information and Control, 19 (1971), 368-374.
• [31] A.S. Skidmore, On the stability of solutions of a differential equation of fourth order. J. London Math. Soc., 41 (1966), 649-661.
• [32] G.P. Szegö, A contribution to Liapunov's second method: Nonlinear autonomous systems. Trans. ASME Ser. D.J.Basic Engrg., 84 (1962), 571-578.
• [33] H.O. Tejumola, Further results on the boundedness and the stability of certain fourth order differential equations. Atti. Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Natur., 52(8) (1972), 16-23.
• [34] H.O. Tejumola, A boundedness theorem for some non-linear differential equations of the fourth order. Atti. Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Natur., 55(8) (1973), 18-24.
• [35] A. Tiryaki and C. Tunç, Construction Lyapunov functions for certain fourth-order autonomous differential equations. Indian J. Pure Appl. Math., 26(3) (1995), 225-232.
• [36] C. Tunç, A study of the stability and boundedness of the solutions of nonlinear differential equations of the fifth order. Indian J. Pure Appl. Math., 33(4) (2002), 519-529.
• [37] C. Tunç, A note on the stability and boundedness results of solutions of certain fourth order differential equations. Applied Mathematics and Computation, 155(3) (2004), 837-843.
• [38] C. Tunç, On the asymptotic behavior of solutions of certain third-order nonlinear differential equations. J. Appl. Math. Stoch. Anal., 2005, no.1, 29-35.
• [39] C. Tunç, Boundedness of solutions of a third-order nonlinear differential equation. JIPAM. J. Inequal. Pure Appl. Math., 6(1) (2005), Article 3, 1-6.
• [40] C. Tunç, Uniform ultimate boundedness of the solutions of third-order nonlinear differential equations. Kuwait J. Sci. Engrg., 32(1) (2005), 39-48.
• [41] C. Tunç, Some stability and boundedness results for the solutions of certain fourth order differential equations, Acta Universitatis Palackiana Olomucensis, Facultas Rerum Naturalium, Mathematica, 44 (2005), 161-171.
• [42] C. Tunç, Stability and boundedness of solutions to certain fourth-order differential equations. Electron. J. Differential Equations, 2006(35) (2006), 1-10.
• [43] C. Tunç, About stability and boundedness of solutions of certain fourth order differential equations, Nonlinear Phenomena in Complex Systems, 9(1) (2006), 380-387.
• [44] V.I. Zubov, Methods of A. M. Lyapunov and their application, Noordhoff Ltd, Groningen 1964, pp. 263.
• [45] X. Wu and K. Xiong, Remarks on stability results for the solutions of certain fourth-order autonomous differential equations. Internat. J. Control., 69(2) (1998), 353-360.

Publication Dates

• Publication in this collection
  10 May 2007
• Date of issue
  2007

History

• Received
  10 July 2006
• Accepted
  03 Jan 2007