Ajuste de parâmetros de interação em modelos termodinâmicos

Interactional parameters fitting in thermodynamics models

AJUSTE DE PARÂMETROS DE INTERAÇÃO EM MODELOS TERMODINÂMICOS

Adair MARTINS^*

Roberto LAURENT^**

Silvia Beatriz AZNAREZ^***

Miguel Angel POSTIGO^***

RESUMO: Para misturas nas quais existem interações entre moléculas diferentes aparece um parâmetro energético de interação ajustável na relação das variáveis. As grandezas termodinâmicas de excesso dão informação qualitativa dos possíveis tipos de interação. Duas grandezas importantes neste sentido são o volume de excesso e a entalpia de excesso. Neste artigo se estudam diferentes métodos, regressão com mínimos quadrados e por minimização do valor absoluto e relativo dos resíduos, para determinar a possibilidade de aplicação dos mesmos no cálculo de parâmetros de interação molecular em modelos termodinâmicos de soluções. Usam-se dados experimentais de volume molar de excesso para todo o intervalo de frações molares de 10 sistemas binários formados por acetonitrila + um álcool primário (do metanol ao n-decanol). Comparam-se os valores calculados e os dados experimentais das grandezas, e são feitas análises dos resultados.

PALAVRAS-CHAVE: Regressão, Mínimos Quadrados, Interação Molecular, Sistemas Binários

Introdução

Existem na literatura diversos modelos termodinâmicos que procuram descrever o comportamento das soluções. O modelo mais utilizado é o de Prigogine-Flory-Patterson e mais recentemente o método ERAS (Extend Real Associated Solution) desenvolvido para soluções associadas [1-6]. Estes modelos estão baseados na descrição do comportamento das soluções em uma equação de estado reduzida, na qual se envolvem propriedades macroscópicas das substâncias puras. No caso de misturas onde existem interações entre moléculas diferentes aparece um parâmetro de interação ajustável na relação das variáveis termodinâmicas. As grandezas termodinâmicas de excesso, especialmente o volume de excesso V^Ee a entalpia de excesso H^E, dão informação qualitativa dos possíveis tipos de interação.

Modelo de Prigogine-Flory-Patterson

Neste modelo considera-se uma expressão aproximada para o V^E em função de três contribuições:

Para o cálculo da contribuição interacional é necessário o conhecimento do parâmetro energético c₁₂ já que os demais parâmetros são conhecidos. O mesmo pode ser calculado a partir dos V^E experimentais resolvendo um modelo de ajuste. O valor do c₁₂ assim obtido permite obter valores teóricos de H^E. Também pode resolver-se o problema inverso da mesma maneira, a partir de dados experimentais de H^Eobter resolvendo um problema de ajuste c₁₂ , e com este, valores teóricos de V^E.

No presente artigo analisa-se a obtenção do c₁₂ a partir da Tabela I de valores experimentais de V^Eobtidos a 298,15 K para diferentes frações molares (x₁) da acetonitrila como primeiro componente [3]. Os segundos componentes são os álcoois primários com cadeias de carbono de 1 a 10 (metanol, etanol, n-butanol, n-propanol, n-pentanol, n-hexanol, n-heptanol, n-octanol, n-nonanol e n-decanol).

Os métodos de ajuste e o problema de robustez

Suponha o caso geral de ajuste de N pontos experimentais (x_i, y_i) a um modelo y(x,a) com um parâmetro ajustável a. O método mais tradicional é o familiar ajuste por mínimos quadrados [10], que consiste em determinar o valor do coeficiente a de maneira que faça mínima a soma dos resíduos absolutos ao quadrado (SRAQ):

Essa expressão rigorosamente leva à minimização da função objetivo Qui-quadrado:

em que os fatores de peso s_i são os desvios padrões das medições em cada ponto. A equação (2) coincide com (3) se os s_isão iguais. A equação (2) dá um resultado ótimo (mais provável) se os erros de medição são aleatórios e respondem a uma distribuição normal (gaussiana). Este não é o atual problema, em que se trata de ajustar uma curva teórica aproximada a uma curva experimental com erros de medição. Aqui os erros de aproximação do modelo (resíduos) são muito maiores que os erros de medição, portanto o ajuste pelo método dos mínimos quadrados pode resultar pouco "robusto".

A "robustez" de um estimador está relacionada com a sua insensibilidade às variações nos dados, pequenos desvios de todos eles e muito especialmente desvios relativamente grandes num pequeno número.

Existem vários métodos sofisticados para resolver estes problemas, bastante difíceis de implementar e utilizar. Um método robusto, que se aplica com muita facilidade a regressão linear, é pela minimização da soma dos resíduos absolutos (SRA):

Da mesma maneira que na equação (3) também se podem considerar fatores de peso s_i . Dado que no presente caso a medição pode assumir-se exata se podem minimizar resíduos relativos, isto eqüivale a considerar desvios padrões relativos iguais em todos os pontos. Para a minimização da soma dos resíduos relativos ao quadrado (SRRQ ) se tem:

e para a minimização da soma dos resíduos relativos (SRR):

Observe que a equação (6) eqüivale a minimizar os resíduos percentuais, resultando uma idéia muito prática já que muitas vezes os resíduos percentuais de um modelo são utilizados para mostrar gráfica ou numericamente a qualidade de um ajuste [2].

Implementação dos métodos de ajuste

Na Figura 1 (a) mostra-se a SRAQ em função de c₁₂ a minimizar para a mistura acetonitrila-decanol. Observa-se uma função com comportamento "muito quadrático". Esse comportamento, que também se verifica para as outras misturas e para a SRRQ, sugere que a utilização da busca unidimensional com primeiras derivadas garante a convergência e que esta será muito rápida [7,10].

Implementou-se em MATLAB [8,9] um algorítmo baseado no método da secante com a derivada calculada numericamente. Em todos os caso se obteve convergência com mais de quatro dígitos significativos num máximo de três iterações independentemente do valor inicial.

Na Figura 1 (b) mostra-se a SRR em função de c₁₂ a minimizar para a mistura acetonitrila-decanol. Observa-se uma função com comportamento "bastante linear" por trechos e com descontinuidade nas derivadas. O mesmo comportamento pode ser observado para as outras misturas e para a SRA. Esse mal comportamento da função faz com que não se possa utilizar o método anterior ou outros baseados em aproximações parabólicas. Tem-se que conformar com um método mais rudimentar e de convergência lenta em duas etapas.

Na primeira etapa é necessário obter um limite máximo e um limite mínimo para a solução e na segunda etapa diminuir sucessivamente este intervalo até uma tolerância preestabelecida.

Para a primeira etapa se desenvolveu um algorítmo baseado na obtenção de raízes através do método de Newton Raphson, com a derivada calculada numericamente. Como a SRA(c₁₂). não tem raíz em algum momento se obtém um ponto em que a derivada muda de sinal obtendo-se o intervalo desejado. Em todas as aplicações se obteve um intervalo num máximo de três iterações independentemente do valor assumido inicialmente. Para a segunda etapa se implementou uma busca unidimensional baseada no conceito de bisseção, a busca pela seção áurea seria outra alternativa [7,10], ambas têm convergência linear mas esta é garantida. Na Figura 2 mostra-se o algorítmo utilizando um esquema de diagrama de chaves. Os programas foram implementandos com o Software MATLAB [8,9].

Análises de resultados

Na Tabela 2 mostram-se os c₁₂ calculados pelos quatros métodos e para as dez misturas. Em geral os resultados são similares mas em alguns casos se observam diferenças bastante significativas.

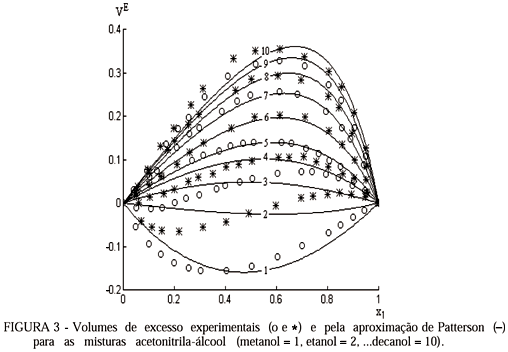
Na Figura 3 mostram-se os resultados experimentais e uma curva de ajuste para cada caso. Observa-se que o modelo teórico funciona razoavelmente bem para a maioria das misturas, com exceção do etanol, butanol e propanol. Isto se deve ao comportamento sigmóide da função experimental que o modelo simplesmente não é capaz de representar.

Para os quatro primeiros álcoois se escolheu o c₁₂ calculado através da SRA e nos restantes através da SRR. Esta escolha foi pelo fato de que para os primeiros álcoois, especialmente as três exceções mencionadas, o c₁₂ baseado em desvios relativos dá excessivo peso aos desvios de alguns valores próximos a zero, fazendo menos coerente ainda a solução. Para as misturas restantes ao ter uma grande diferença entre valores máximos e mínimos o c₁₂ baseado em desvios relativos dá resultados mais equilibrados.

Da Tabela 2 pode-se observar que para os sete primeiros álcoois não existem diferenças significativas entre o c₁₂ calculado através da SRAQ e da SRA , obtendo-se ajustes quase coincidentes. As diferenças começam a ser importantes a partir do octanol e são muito notáveis para o decanol (-0.4862 contra -1.6066), a diferença se deve a que o método dos mínimos quadrados dá maior peso aos resíduos próximos aos valores máximos da função, enquanto os métodos baseados em resíduos absolutos atuam em forma mais equilibrada. Este efeito observa-se na figura 4, onde mostram-se os resíduos relativos em percentagem para ambos os métodos.

Com relação ao c₁₂ calculado com a SRRQ se obtiveram praticamente os mesmos resultados que com a SRR..

Conclusões

O ajuste pelo método dos mínimos quadrados pode não se adaptar bem ao problema de ajustar um parâmetro de um modelo teórico aproximado a dados experimentais (parâmetro energético c₁₂ do modelo de volume de excesso de uma mistura binária acetonitrila-álcool primário neste caso) devido ao fato de se estar muito longe de cumprir com a hipótese de resíduos com distribuição normal. O método pode dar um excessivo peso aos resíduos próximos aos valores máximos da função. Nas análises realizadas este efeito foi notável para a mistura acetonitrila-decanol. Os métodos baseados em mínimos quadrados podem utilizar algoritmos que usam aproximações quadráticas de convergência rápida.

Métodos mais "robustos" são então convenientes para resolver melhor o problema. O método baseado em resíduos absolutos é uma alternativa muito fácil de implementar. A implementação de métodos baseados em resíduos absolutos requer um algorítmo em duas etapas. A primeira consiste na determinação do intervalo que contém o mínimo (foi proposta uma adaptação do método de Newton Raphson para este fim) e a segunda na aplicação de um método iterativo do tipo bisseção ou busca pela seção áurea, ambos com convergência linear mas esta é garantida.

A minimização de resíduos relativos (percentuais) é uma interessante variante prática, já que estes erros percentuais em geral são uma medida mais clara e intuitiva para dar idéia da qualidade de um ajuste ou modelo. Mas em alguns casos podem dar excessivo peso aos resíduos correspondentes aos valores da função proximos a zero.

MARTINS, A. et al. Interactional parameters fitting in thermodynamics models. Ecl. Quím. (São Paulo), v.25, p. , 2000.

ABSTRACT: For mixtures in which exist interactions between differents molecules, in the relationship of the variables appears an energetic adjustable parameter of interaction. The thermodynamic properties of excess give qualitative information of the possible types of interaction. Two important properties in this sense are the excess volume and excess enthalpy. In this paper different methods are studied, regression with least squares and by minimizing absolute and relative residues, to determine their possibilities of application to evaluate molecular interaction parameters in thermodynamic models of solutions, using experimental data of excess molar volume for the whole composition ranges of 10 binary systems of molar fractions formed by acetonitrile + primary alcohol (from metanol to n-decanol). The calculated values and the experimental data of the properties are compared, and the comparative results are analyzed.

KEYWORDS: Regression, Least Squares, Interaction molecular, Binary Sistems

Recebido em 11.8.1999

Aceito em 7.12.1999

** Departamento de Electrotecnia, F.I, UNC.

*** Departamento de Química, F.I, UNC.

• 1 ABE, A.; FLORY, P. J. The thermodynamic properties of mixtures of small, nonpolar molecules. J. Am. Chem. Soc. v.87, p.1838, 1965.
• 2 AWWAD ,A.M., AL-NIDAWY, N.K., SALMAN, M.A.; HASSAN, F.A. Molar excess volumes of binary mixtures of ethylbenzene with n-alkanes at 298.15 K, an interpretation in terms of the Prigogine-Flory-Patterson model.. Thermochimica Acta, v.114, p.337-46, 1987.
• 3 AZNAREZ, S.; POSTIGO, M., Volumenes molares de exceso de mezclas binarias de acetonitrilo con alcoholes primarios a 298,15 K, X Congreso Argentino de Fisicoquímica, Tucumán, Argentina, 1997.
• 4 FLORY P.J. Statistical Thermodynamics of Liquid Mixtures. J.Am. Chem. Soc. v.87, p.833, 1965.
• 5 HEINTZ, H.; BER BUNSENGES, A., A new Theoretical Approach for predicting Excess Properties of Alkanol/Alkane mixtures, Phys Chem. v.89, p.172, 1985.
• 6 LETCHER, T.M.; BAXTER, R.C., Application of the Prigogine-Flory-Patterson theory part I. Mixtures of n-alkanes with bicyclic components, benzene, cyclohexane and n-hexane. Journal of Solution Chemistry, v.18, n°1, 1989.
• 7 LUENBERGER, D.G., Introduction to linear and non-linear programming, Addison-Wesley, Reading, 1973.
• 8 Math Works, Inc., MATLAB for Windows Reference Guide, 1992
• ⁹
  Math Works, Inc., MATLAB for Windows User’s Guide, 1993.
• 10 Press W. H., Numerical Recipes - The art of Scientific Computing, Cambrige University Press, 1986.

*

Departamento de Informática y Estadística, F.E.A, UNC. Buenos Aires 1400, 8300 Neuquén, Argentina.

Datas de Publicação

• Publicação nesta coleção
  26 Nov 2002
• Data do Fascículo
  2000

Histórico

• Recebido
  11 Ago 1999
• Aceito
  07 Dez 1999