FE analysis of laminated composite plates using a higher order shear deformation theory with assumed strains

FE analysis of laminated composite plates using a higher order shear deformation theory with assumed strains

Sang Jin Lee^*; Ha Ryong Kim

ADOPT Research Group, Department of Architectural Engineering, Gyeongsang National University, Republic of Korea

ABSTRACT

A study on the finite element (FE) analysis of laminated composite plates is described in this paper. In order to investigate structural behavior of laminated composite plates, a four-node laminated plate element is newly developed by using a higher order shear deformation theory (HSDT). In particular, assumed natural strains are introduced in the present FE formulation to alleviate the locking phenomenon. Several numerical examples are carried out and its results are then compared with the existing reference solutions. It is found to be that the proposed FE is very effective to remove the locking phenomenon and produces reliable numerical solutions for most laminated composite plate structures.

Keywords: Laminate Composite Plate, Finite Element, Higher Order Shear Deformation, Locking Phenomenon, Assumed Strain Method

1 INTRODUCTION

Laminated composite plates have been extensively used in many engineering disciplines such as civil engineering, marine engineering and aerospace engineering due to its high strength to weight ratio and excellent corrosion resistance. With the growing use of laminated composite material, it becomes very important to conduct numerical analysis and to use the resulting information in the structural design process. This situation clearly has demanded the development of efficient and accurate numerical analysis techniques which are necessarily required to predict the behaviors of laminated plates.

In the early days, classical laminated plate theory (CLPT) has been mainly used with negligence of the effect of transverse shear deformation. However, due to the increasing use of thick laminated plate in construction, thick plate theories such as the first order shear deformation theory (FSDT) and the higher order shear deformation theory (HSDT) are needed to take into account transverse shear deformation through the thickness direction of the plates. In particular, The HSDTs do not required shear correction factor and it can generally guarantee zero transverse shear stress values on the top and bottom surfaces of the plate. Some important and early works on HSDT can be found in the open literatures [1-5] where more realistic representation of transverse shear deformation were generally tried to be provided. Later, Zhang and Yang [6] described some recent developments of the FEs based on various laminated composite plate theories. Reddy [1] suggested a simple but very useful HSDT for laminated composite plates. His version of HSDT is based on equivalent single layer plate theory and it allows parabolic variation of transverse shear stress and also satisfies zero shear stress boundary conditions at the top and bottom surfaces of the plate. Moreover, it does not involve any unknown fields which do not have any physical meaning. Bose and Reddy [7, 8] analyzed laminated plates by using a unified third-order laminate plate theory that contains classical, first-order and third-order theories and they presented analytical method using the Navier and Levy equations and the FE method using the unified third order laminate plate theory. A review on the various methods used in the estimation of transverse and inter-laminar stresses for laminated composite plates and shell including both analytical and numerical methods was provided by Kant and Swaminathan [9]. Kant and Manjunatha [10] provided the FE based on HSDT having twelve degrees of freedom per node. They presented three-dimensional stress and strain states to investigate the flexure-membrane coupling behavior of unsymmetrical laminated plate. Akhars and Li [11] developed a spline finite strip method for static and free vibration analysis of composite plates using Reddy’s HSDT. Pervez et al [12] developed a two dimensional serendipity FE based on a refined HSDT having seven degrees of freedom per node to perform the linear static analysis of laminated orthotropic composite plates. Latheswary et al [13] studied the behavior of laminated composite plates under static loading by using a four-node nonconforming element based on HSDT. Goswami [14] presented a simple C^0 FE formulation for nine-node FE with six degrees of freedom based on HSDT.

From literature review, the previous FE developments using HSDT have mostly depended on the standard strain definition. From this context, as shown in a recent work [15] laminated composite plate FEs based on HSDT can produce the shear locking phenomenon. However, this problem has not been paid much attention and uniform or selective reduced integration technique is just adopted to rectify locking phenomenon although the assumed strain method becomes very popular for the FE analysis of single-layered isotropic plate structures. So far, there have been a few research works on the free vibration analysis of laminated plate using HSDT together with assumed strain method [16, 17]. However, we found that there is no introduction of assumed strains in the formulation of laminated composite plate element based on the HSDT for FE stress analysis, although the stress evaluation at the layer and inter-layer of the laminated plate is very crucial. Therefore, we here propose a new assumed strain laminated composite plate FE based on the HSDT and provide a series of benchmark tests to prove its capability. More specifically, we provide the description on the four-node lower order laminate composite plate FE with assumed strains and its numerical results as benchmark test suites for an application of assumed strains into the laminated composite structures.

2 REVIEWS ON HSDT

2.1 Displacement definition

The total domain () of laminated plate consists of the mid-surface and the thickness as shown in Figure 1 and it can be defined as

where is the xy-plane and is denoted as thickness of plate.

In order to represent the shape of transverse shear deformation in realistic way, the displacement fields may include higher order terms as follows [1]

where , , are the translational displacements in the , , direction respectively, , , are the in-plane displacement, is the transverse displacement of a point on the mid-surface, is the normal rotation in plane, is the normal rotation in plane, are the slopes of the tangents of the deformed mid-surface in the , direction and

2.2 Strain definition

The strains in the plate are defined by linear strain-displacement relationship as follows

Substituting (2) into (3) yields

in which is the in-plane strain term, denotes the transverse shear strain term, and the parameters and are and respectively and the individual strain terms are

2.3 Constitutive equation

In this study, each layer of laminate plate is assumed as orthotropic material and the normal transverse stress is assumed to be negligible. Therefore, the constitutive equation for the layer with respect to the material coordinate system can be written as

in which are the components of rigidity matrix for the layer as follows

where , are the Young’s modulus in direction respectively, , , are the shear modulus and , are the Poisson ratios.

If the angle between the material coordinate system and the global coordinate system is once determined as shown in Figure 1, the transformation can be possible between two coordinate systems.

Therefore, stresses and strains , in global coordinate system can be obtained by using the transformation matrix and stresses and strains , in material coordinate system:

where the transformation matrix between material coordinate system and global coordinate system can be written as

where and in which is the fiber’s angle as shown in Figure 1.

The stress-strain relationship in the global coordinate system can be written by using (6) and (8) as follows

2.4 Stress resultants

The stress resultants are calculated by integration of the stresses through thickness direction of laminated plate and five stress resultant terms such as can be obtained as follows

where is the number of layers in laminated plate.

The above stress resultant terms can be rewritten in the matrix form:

Where the components of the rigidity matrices can be written as follows

and the above equation can be explicitly rewritten in the following form:

3 FINITE ELEMENT FORMULATION

3.1 Kinematics and displacement field

In this study, a four-node plate element having seven degrees of freedom per node is formulated using the isoparametric formulation. Therefore the geometry and displacement fields of the present FE can be defined in the following form:

where is the bilinear Lagrange shape function associated with node , is the position vector of the plate and the nodal displacement vector has seven components such as

where , are two additional degrees of freedom related to the higher order terms of (2) which do not appear in the FE based on the FSDT.

3.2 Strain-displacement relationship matrix

Using (15), the strains of (4) can be rewritten in the form of the strain-displacement relation matrix as follows

where the sub-matrices of are

3.3 Total potential energy of plate

The total potential energy of the laminated plate can be written by using the stress resultants and the corresponding strains as follows

In the discretized FE domain, total potential energy can be written as

By minimization of the total potential energy, with respect to the nodal values we obtain

where is global vector of nodal displacements with typical nodal displacement sub-vector for node a , is the global vector of nodal forces with typical nodal force sub-vector for node a and is the global stiffness matrix where

where is the finite element assembly operator and the element stiffness matrix is divided into five contributions

3.4 Substitute strain-displacement matrix via assumed strain method

In this study, the assumed strain method is employed to alleviate the possible locking phenomenon. Therefore, assumed strains are derived by using the interpolation functions based on Lagrangian polynomial and the strain values at the sampling points where the locking does not exist.

For natural assumed transverse shear strains and , the following sampling points [18] are employed as shown in Figure 2:

Using (24), the assumed natural strains can be defined in the following form

where denotes the position of the sampling point as shown in Figure 2 and the interpolation functions , are employed as follows

Transverse shear strain-displacement relationship produced by assumed strain method can be written in the following matrix form:

where is the assumed natural strain-displacement relationship matrix and explicitly can be written as

in which the , , are

where are the coordinates of nodal point in global coordinate system and natural coordinate system respectively.

3.5 Substitute element stiffness matrix for transverse shear

In previous section, the assumed strains are defined in natural coordinate system and so transverse shear rigidity matrix of (13) can be also defined in the natural coordinate system as follows

Consequently, transverse shear stiffness terms of (23) can be rewritten as follows

In this study, (31) will be used instead of the terms and in (23). Note that the standard FE (HAD4) is derived by using the original terms in (23).

4 NUMERICAL EXAMPLES

In order to investigate the accuracy and reliability of the newly developed laminated plate element HSA4, a series of numerical test for symmetric and unsymmetric laminated plates are considered. The square plates with the simply supported boundary conditions are used in the test. More specifically, two sets of boundary conditions, and are employed in numerical tests as follows

and the three sets of material properties are used as follows

In this study, the laminated plates are also assumed to be subjected to sinusoidal load or uniform load as follows

All the numerical results provided in Tables and Figures are described as non-dimensionalized values by using the following form

Note that the deflection is calculated at the center of the plate and the stresses are produced at the nearest Gauss point to the following locations

where is the width of the plate and is the thickness of the plate.

It should be noted that Reddy’s displacement function definition of (2) can reserve zero shear stress boundary condition at the top and bottom of the laminated plate but this condition cannot be reserved anymore when assumed strain method is adopted with the HSDT. Therefore, the following modified strain definition is used when we calculate transverse shear stress value together with (10):

With (37), we can enforce the values of to zero at top () and bottom () of laminated plates and eventually the zero shear stress values can be achieved at the top and bottom of the plates.

4.1 Symmetric cross-ply () square laminated plate

(a) Convergence rate test: A four-layer symmetric cross-ply () laminated composite plate is analyzed to check the convergence rate of the present FE (HSA4) and its performance for the variation of thickness values. In this test, material property, boundary condition and load case such as are used. Five cases with , , , and FE meshes are employed in the test. Two aspect ratios , 100 are used in FE analysis to show the applicability of the present plate element to both thin and thick plates. The center deflection and stresses are calculated for both thick and thin plates and summarized in Tables 1 and 2. The present solutions are compared with the exact elasticity solution [19] and a FE solution [14]. The convergence test result is plotted in Figure 3.

The present plate element shows a good convergence rate. In particular, we can see that the present FE solution has a good agreement with the elasticity solution [19] and achieves a certain level of convergence with the case of FE mesh for both thin and thick plates. We therefore decided to use the FE mesh with 256 four-node elements for numerical test throughout this study. Note that FE reference solution [14] was produced by a nine-node plate element so that the reference solution with FE mesh is compared to the present solution with the FE mesh.

(b) Locking test: The same plate is also used to investigate the possible appearance of locking phenomenon again. For this purpose, we use four different aspect ratios such as with the FE mesh. Numerical results such as central deflection and stresses of the plate are summarized in Table 3 and it is compared with the solutions produced by elasticity solution [19], Reddy [1], Akhras and Li [11] and Pervez et al [12]. It is found to be that both the present FE HAS4 and the standard FE HSD4 have a good agreement with reference solutions for thick plate situations such as 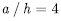and 10. However, if the aspect ratio becomes a larger value, i.e. the plate becomes thin, the four node standard plate element HSD4 has some discrepancies with reference solutions. Specifically, for the aspect ratio 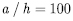, the HSD4 has around 50% of error compare to the reference solutions. It can be considered as the evidence that HSD4 exhibits the shear locking phenomenon when the plate becomes thinner. However, the present plate element alleviates the shear locking phenomenon very effectively with full integration and enhances its performance in great manner as shown in Table 3. We provide the distributions of in-plane stresses and transverse shear stresses , through the thickness direction in Figures 4-7 for .

The stress values produced by the present HSA4 have also good agreements with reference solution for in-plane stress and transverse shear stress 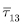. However, the standard FE HSD4 has a huge discrepancy with the present solution for thin plate with the aspect ratio From direct comparison between the present solution and the solution produced by the standard FE, we can identify the locking disappear in the present solution. We here provide numerical results for as a benchmark solution for future study since the stress distributions produced by a FE based on HSDT is few in literatures.

4.2 Unsymmetric cross-ply (

) square laminated plate

This example is used to investigate the performance of the present FE HSA4 on the analysis of unsymmetric composite plate. A two-layer unsymmetric cross-ply () laminated plate is analyzed in the test. The material property, boundary condition and load case such as are used. The central deflection and stresses are calculated for four aspect ratios and summarized in Table 4.

The numerical results are compared with the exact elasticity solution [19], analytical solutions [2, 8] and the FE solution [20]. In this example, we found that the present solutions have good agreements with the reference solutions regardless of aspect ratios. In specific, stress values are reasonably accurate for all aspect ratios .

4.3 Unsymmetric angle-ply (

) square laminated plate

(a) Uniform load (

): The unsymmetric angle-ply (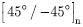) laminated plate are analyzed with four aspect ratios 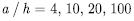with three different numbers of layers such as n=2, 4, 8. Material properties, boundary condition and load case are used as 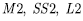respectively. The numerical results are non-dimensionalized and summarized in Table 5. From numerical results, both the present HSA4 and the standard HSD4 have good agreements with reference solution [9] for the aspect ratio 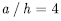. However, for the aspect ratio 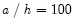the standard FE HSD4 shows a great discrepancy with the reference solution although it exhibit reasonably good performance up to 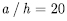. However, the present FE HSA4 does not show any shear locking phenomenon for thin angle-ply unsymmetric laminated plate. In this section, we also investigate the effect of different of layer number on the central deflection with the assumption that plates keep the same total thickness value. From numerical result, when we double the number of layers from n=2 to n=4, the center deflection is reduced up to 60% in case of the aspect ratio 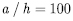and 25 % for aspect ratio 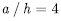respectively. In other words, thick laminated plate is very sensitive to variation of the number of layers than thin laminated plate. We also found that the increase of the number of layers in laminated plate generally tends to reduce the deflection of laminated plate when the plate has the same thickness value.

(b) Sinusoidal load (

): In this example, the analysis of unsymmetric angle-ply (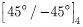) laminated plate is carried out with two aspect ratios 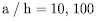and sinusoidal load. This example provides the results of more detailed investigation on the performance of the present FE HSA4 for unsymmetric angle-ply plate. Material properties, boundary condition and load case are used as 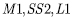respectively. The non-dimensionalized deflection and stresses are summarized in Table 6. From numerical results, the HSA4 has excellent agreements with the reference solutions [10, 13]. However, the standard FE HSD4 has the error of 35% compared to the reference solutions for aspect ratio 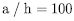. Figures 8 and 9 show the variation of non-dimensionalized in-plane stress 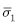and transverse shear stress 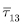through the thickness direction for the aspect ratios 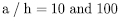. In particular, the present element HSA4 can produce a good parabolic shape than that of HSD4 for the transverse shear stress 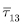as shown in Figures 8 and 9. The present FE shows also a good performance to predict the maximum stress value of in-plane stress 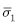and transverse shear stress .

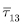4.4 Unsymmetric cross-ply () square sandwich plate

The analysis of a five-layer unsymmetric and unbalanced sandwich plate with isotropic core is carried out and its numerical results are presented. Material properties, boundary condition and load case are used as respectively. The thickness of core is equal to total thickness of four face sheets which have all the same thickness. The non-dimensionalized deflection and in-plane stresses are summarized in Table 7. From numerical results, both HSD4 and HSA4 have a good agreements with the reference solutions up to the aspect ratio . For the aspect ratio 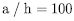, the present element HSA4 have approximately the 1-8 % of differences with reference solutions [1, 21] but the standard HSD4 have almost the 60 % of difference with the reference solutions because of locking phenomenon.

5 CONCLUSIONS

A four-node laminated composite plate element having seven degrees freedom per node is newly developed by using the HSDT and assumed strains to perform the FE stress analysis. The accuracy and reliability of new laminated composite plate element is thoroughly tested by using five numerical tests for both symmetric and unsymmetric situations. From numerical results, the present FE does not produce any locking phenomenon for the cases with very small aspect ratio of the plate and it can be applicable to most types of laminated composite plate structures. Further investigation into the performance of the present FE for the case subjected to concentrated or line loads is underway and the vibration, stability and transient response of laminated plates are also of prime importance as future investigations.

Acknowledgements The research grants from the Ministry of Construction & Transportation, Korea, for the Construction Technology Research & Development Program (PN: 06-R&D-B03) are gratefully acknowledged.

Received 01 Mar 2012

In revised form 05 Aug 2012

• [1] Reddy JN. A simple Higher order Theory for laminated composite plates. ASME J Appl Mech 1984;51:745-752.
• [2] Bert CW. A critical evaluation of new plate theories applied to laminated composites. Compos Struct 1984;2:329-347.
• [3] Lo KH, Christensen RM, Wu EM. A high-order theory of plate deformation-part 2: laminated plates. Appl Mech 1977;44:669-676.
• [4] Reddy JN. A review of the literature on finite element analysis of progressive failure in laminated composite plates. Shock Vib Digest 1985;17(4):3-8.
• [5] Reddy JN. Mechanics of laminated composite plate. CRC Press, 1997.
• [6] Zhang YX, Yang CH. Recent developments in finite element analysis for laminated composite plates. Compos Struct 2009;88:147-157.
• [7] Bose P, Reddy JN. Analysis of composite plates using various plate theories. Part 1: Formulation and analytical solutions. Struct Engng Mech 1998;6(6):583-612.
• [8] Bose P, Reddy JN. Analysis of composite plates using various plate theories. Part 2: Finite element model and numerical results. Struct Engng Mech 1998;6(7):727-746.
• [9] Kant T, Swaminathan K. Estimation of transverse/interlaminar stresses in laminated composites-a selective review and survey of current developments. Compos Struct 2000;49:65-75.
• [10] Kant T, Manjunatha BS. An unsummetric FRClaminate C⁰ finite element model with 12 degrees of freedom per node. Eng Comput 1988;5:300-308.
• [11] Akhras G, Li W. Static and free vibration analysis of composite plates using spline finite strips with higher order shear deformation. Compos Part B: Eng 2005;36:496-503.
• [12] Pervez T, Seibi AC, Al-Jahwari FKS. Analysis of thick orthotropic laminated composite plates based on higher order shear deformation theory. Compos Struct 2005;71:414-422.
• [13] Latheswary S, Valasrajan KV, Rao YVKS. Behavior of laminated composite plates using higher order shear deformation theory. IE(I) J-AS 2004;85:10-17.
• [14] Goswami S. A C⁰ plate bending element with refined shear deformation theory for composite structures. Compos Struct 2006;72:375-382.
• [15] Lee SJ, Kim HR. Finite element analysis of symmetric and unsymmetric laminated plates based on higher order shear deformation theory. In: Proceedings of Autumn Congress of Architectural Institute of Korea, Cheongju, 26-27 Oct 2007.p. 249-252.
• [16] Nayak AK, Moy SSJ, Shenoi RA. Free vibration analysis of composite sandwich plates based on Reddy`s higher -order theory. Compos Part B: Eng 2002;33:505-519.
• [17] Nayak AK, Shenoi RA. Assumed strain finite elements for buckling and vibration analysis of initially stressed damped composite sandwich plates. Sandwi Struct and Mater 2005;7:307-334.
• [18] Lee SJ. Free-vibration analysis of plates by using a four node finite element formulated with assumed natural transverse shear strain. J Sound Vibration 2004;278:657-684.
• [19] Pango NJ. Exact solutions for rectangular bidirectional composites and sandwich plates. J Compos Mater 1970;4:20-34.
• [20] Kant T, Pandya BN. A simple finite element formulation of a higher order theory of unsymmetrically laminated composite plates. Compos Struct 1988;9:215-246.
• [21] Kant T, Swaminathan K. Analytical solutions for the static analysis of laminated composite and sandwich plates based on higher order refined theory. Compos Struct 2002;56:329-344.

Publication Dates

• Publication in this collection
  01 Mar 2013
• Date of issue
  May 2013

History

• Received
  01 Mar 2012
• Reviewed
  05 Aug 2012