Abstracts
We study the intertemporal consumption and investment problem in a continuous time setting when the security prices follow a Geometric Lévy process. Using stochastic calculus for semimartingales we obtain conditions for the existence of optimal consumption policies. Also, we give a charaterization of the equivalent martingale measures.
Lévy processes; incomplete markets
Estudamos o problema do consumo e investimento intertemporal em tempo contínuo, quando os preços dos ativos seguem um processo de Lévy Geométrico. Usando cálculo estócastico para semimartingalas obtemos condições para a existência de políticas ótimas de consumo. Também, mostramos a caracterização das medidas martingalas equivalentes.
Optimal consumption and investment with Lévy processes* * I want to thank Maria Eulália Vares for valuable comments and IMPA-Brazil, where this project was partially developed. I also acknowledge financial support from CNPq, Brazil.
José Fajardo Barbachan
IBMEC Business School. E-mail: pepe@ibmecrj.br
ABSTRACT
Summary: 1. Introduction; 2. Model; 3. Lévy processes and equivalent martingale measures; 4. Optimization problem; 5. Choosing a measure; 6. Example; 7. Conclusions.
We study the intertemporal consumption and investment problem in a continuous time setting when the security prices follow a Geometric Lévy process. Using stochastic calculus for semimartingales we obtain conditions for the existence of optimal consumption policies. Also, we give a charaterization of the equivalent martingale measures.
Keywords: Lévy processes; incomplete markets.
JEL Codes: G11; C61.
RESUMO
Estudamos o problema do consumo e investimento intertemporal em tempo contínuo, quando os preços dos ativos seguem um processo de Lévy Geométrico. Usando cálculo estócastico para semimartingalas obtemos condições para a existência de políticas ótimas de consumo. Também, mostramos a caracterização das medidas martingalas equivalentes.
1 Introduction
The intertemporal optimal consumption and investment problem in a continuous time setting is a important task in the finance literature. The first to study this problem was Merton (1971), using stochastic dynamic programming he obtained explicit solutions for an economy with incomplete markets in which security prices follow a geometric Brownian motion, the endowments follow a Poisson process and the investor has a negative exponential utility with an infinite horizon.
Many other authors have tried to improve the above model adding income stream, transaction costs, borrowing constraints and other facts that make the model more real. In all these models the log-Normal hypothesis or a slight modification of it is assumed for stock returns. Unfortunately, it is very well known that this hypothesis did not hold for the majority of stocks, since they present stylized facts like: fat tails, asymmetry, autocorrelation, etc. For a survey about the principal results on stylized facts see Rydberg (1997).
For this reason, recently some results, assuming more general process to model stock returns, have appear in the literature. Kramkov and Schachermayer (1999) prove that if the asymptotic elasticity of the utility is strictly less than one, then there is a solution for the optimal consumption and investment problem.
Benth et al. (2001) have obtained a solution for the optimal consumption-investment problem assuming that the dynamic programming principle holds and that the stock returns are modelled by a pure-jump Lévy processes, to solve this problem they used a viscosity solution approach. Fajardo (2000) proves that when the stock returns follow a Hyperbolic Lévy motion and we choose a particular equivalent martingale measure (EMM) to construct the state price density, then it is possible to find conditions on the wealth process and strategies that guarantee the existence of optimal policies.
In this paper we extend the latter result considering a huge class of processes called geometric Lévy processes and all the set of EMM. To this end we characterize all the EMM that exist in the market. The paper is organized as follows: in section 2 we describe the model, in section 3 we address the existence of EMM in a Lévy market, that is, when stock prices follow a Geometric Lévy Motion. In section 4 we introduce the optimal problem and state the main result. In section 5 we show how to choose an EMM and in the last sections we present an example and the conclusions.
2 Model
We will consider a financial market  consisting of 2 assets. The first is called bond (the riskless asset) and the second is called stock (the risky asset). We denote by B(t) and P(t) the bond's and stock's price at each time t Î [0,T], respectively. The evolution of these prices are modelled by the following equations:
consisting of 2 assets. The first is called bond (the riskless asset) and the second is called stock (the risky asset). We denote by B(t) and P(t) the bond's and stock's price at each time t Î [0,T], respectively. The evolution of these prices are modelled by the following equations:
In this model the sources of risk are modelled by a Lévy process Y (t),0 < t < T, i.e., a process with independent and stationary increments. Y is defined on a given complete probability space (W, 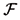 , P) and denote by F = {
, P) and denote by F = {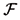 (t), 0 < t < T} the P augmentation1
1
The augmented filtration
F is defined by
(
t) = s(
Y(
t) È
), where
= {
E Ì W : $
G Î
with
E Í
G,
P (
G) = 0} denotes the set of
P- null events.
of the natural filtration generated by Y:
(t), 0 < t < T} the P augmentation1
1
The augmented filtration
F is defined by
(
t) = s(
Y(
t) È
), where
= {
E Ì W : $
G Î
with
E Í
G,
P (
G) = 0} denotes the set of
P- null events.
of the natural filtration generated by Y:
time horizon will be considered finite. The positiveness of the stock price will be analyzed in the next section. The interest rate {r(t):0 < t < T}, assumed finite, the appreciation rate {r(t),0 < t < T}, and the volatilities s(t),0 < t < T will be referred as the coefficients of the financial market  . We assume that these coefficients are deterministic continuous functions. Now we introduce a small investor (his decisions does not affect the market prices), who will decide at each moment t Î [0,T]:
. We assume that these coefficients are deterministic continuous functions. Now we introduce a small investor (his decisions does not affect the market prices), who will decide at each moment t Î [0,T]:
1. How much money p(t) he wants to invest in the stock;
2. His cumulative consumption C(t).
Of course, these decisions must be made without foreknowledge of future events, so C and p must be adapted processes. 2 2 We said that a process { Xt} is adapted with respect to F if for all t Î [0, T], Xt is an ( t)-measurable random variable. If we denote by X(t) the agent's wealth at time t, then the amount invested in the bond will be X(t) p(t). From here, (1) and (2), we obtain the following equation for the wealth:
The solution of this linear stochastic differential equation with initial condition x Î 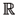 , i.e. X(0) = x is:
, i.e. X(0) = x is:
for all 0 < t < T. Where
is the discount factor in  . Now we give some definitions:
. Now we give some definitions:
Definition 1
(i)An F adapted process C = C(t), 0< t < T with nondecreasing, right-continuous paths, left-hand limits and C(0) = 0,C(T) < ¥ a.s is called a cumulative consumption process.
(ii) An F progressively measurable, càdlàg,
valued process p = {p(t),0 < t < T} with
is called a portfolio process.
(iii) For a given x Î 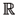 and (p, C) as above, the process X(t) = Xx,p,C(t) of (3), (5) is called the wealth process corresponding to initial capital x, portfolio p, and cumulative consumption process C.
and (p, C) as above, the process X(t) = Xx,p,C(t) of (3), (5) is called the wealth process corresponding to initial capital x, portfolio p, and cumulative consumption process C.
It is important to notice that (X(t) p(t)) and p(t) can take negative values, in other words short-sales of stock and borrowing at interest rate r(·) are allowed. So we need to impose some restriction on portfolios.
Definition 2: We say that a given portfolio process p(·) is tame, if the associated discounted gain process:
is a.s. bounded from below by some real constant:
Condition (9) is necessary to avoid doubling strategies, that is, portfolios that attain arbitrary large values of wealth with probability one at t = T, starting with zero initial capital at t = 0.3 3 See Karatzas and Shreve (1998) for an example.
Definition 3 A tame portfolio that satisfies:
is called an ''arbitrage opportunity'' (or free lunch). We say that a market
is arbitrage free if no such portfolio exist.The free lunch interpretation of (10) is clear: starting with zero initial capital and using the strategy p(·) at the end of the period t = T. Since g(T) = B(T)1, we have X(T) = X0,p,0(T) = B(T)Mp(T), then X(T) > 0 a.s, i.e. no risk and positive probability of gain P[X(T) > 0] > 0.
So we need conditions for precluding these arbitrage opportunities. We know that the existence of an EMM in general context rule out this opportunities. In our context Eberlein and Jacod (1997) show that when r(t) = r, "t Î [0,T], there would be EMM and Chan (1999) shows analogous result with r(·) being a deterministic continuous function. We will show that these existence imply that our market is arbitrage free. An important consequence of our extension is that many market models are incomplete then we have not an unique EMM. The criterion to choose one of these EMM will be also presented.
3 Lévy Processes and Equivalent Martingale Measures
In this section we characterize all the equivalent martingale measures in the model introduced in section 2. We know that all the infinitely divisible distributions4 4 An infinite divisible distribution generates a Lévy processes, for abuse of notation we use Yt for both. For more details see Sato (1999) or Shiryaev (1999). (Yt) admit the following Lévy-Khintchine representation:
where f is the characteristic function of the infinitely divisible distribution, a is the drift, c is the quadratic variation coefficient and G is a positive measure with òminx2,1G(dx) < ¥. This measure is called the Lévy measure and describes the jumps of the process.
We also know that all Lévy process must be a linear combination of a standard Brownian Motion (Wt) and a quadratic pure jump process5 5 A process X is said to be a quadratic pure jump process if cº 0, where c is the continuous part of its quadratic variation . Remember that is the process such that ( Nt) 2 t is a martingale. (Nt) which is independent of the Brownian Motion Wt, then
Yt= cWt + Nt
The process Nt has a Lévy decomposition: Let L(dt, dx) be a Poisson measure on 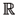 + ×
+ × 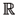 \0 with expectation (or compensator) measure dt × G 6
6
"
B Î
×
\0,
L(
B) has Poisson distribution with parameter (
dt ×
G)(
B)
, then:
\0 with expectation (or compensator) measure dt × G 6
6
"
B Î
×
\0,
L(
B) has Poisson distribution with parameter (
dt ×
G)(
B)
, then:
Now assume that7 7 E(·) denote the expectation with respect to P
E[exp(bY1)] < ¥"b Î (-b1, b2)
and
ebxdG(x) < ¥"b Î (b1, b2)where 0 < b1, b2< ¥ . The first assumption said that Yt has all moments finite and the second is technical and will let us separate integrands. With this in mind we can return to the jumps and transform the equation (12) into:
Nt =  (L((0, t], dx) tG(dx)) + tEN1
(L((0, t], dx) tG(dx)) + tEN1
It is easy to see that the process
Mt =  (L((0, t], dx) tG(dx))
(L((0, t], dx) tG(dx))
is a martingale. Then Nt = Mt + at, with a = EN1, as a consequence the original process can be written as
Before passing to characterize the absolutely continuous measures with respect to the original measure, let us introduce some elements of stochastic calculus: for any measurable function f(t, x) we have
and for any C2 function f, we have the Generalized Itô's formula for càdlàg semimartingales X1, ..., Xn:
with  ,
,  and [Xi, Xj]c the continuous part of the mutual variation8
8
For more details see Shiryaev (1999).
of Xi and Xj.
and [Xi, Xj]c the continuous part of the mutual variation8
8
For more details see Shiryaev (1999).
of Xi and Xj.
Now with the above results we study the solution of equation (2):
dP(t) = P(t)[rtdt + stdY(t)] = (ast + rt)Ptdt + stPt(cdWt + dMt)
When the coefficients rt and st are deterministic continuous function the solution of this equation is given by the Doléans-Dade exponential:9 9 See Jacod and Shiryaev (1987)
with (13) we obtain:
to ensure that Pt > 0, a.s. "t Î [0, T], we need that
1 + stDMt > 0, "t Î [0, T]
If we assume the convention 's > 0', we only need that the jumps of Nt be bounded from below10
10
Observe that from
Nt =
Mt +
at we have D
Mt = D
Nt.
, i.e., DNt >  , it means that we consider only ''semi-fat tailed'' distributions as Poisson, Gamma, Hyperbolic and Normal Inverse Gaussian and we eliminate processes with heavy tails, it is worth noting that the stable distributions (without including the Gaussian Case) were eliminated when we supposed that Y has all moments finite.
, it means that we consider only ''semi-fat tailed'' distributions as Poisson, Gamma, Hyperbolic and Normal Inverse Gaussian and we eliminate processes with heavy tails, it is worth noting that the stable distributions (without including the Gaussian Case) were eliminated when we supposed that Y has all moments finite.
The following step consist in characterize all the measures that are absolutely continuous with respect to P, to this end let:
 (dt,) = L(dt, dx) dtG(dx)
(dt,) = L(dt, dx) dtG(dx)
then
Now two useful results:11 11 See Chan (1999)
Lemma 1Let Rt and K (t,x) be a previsible and a Borel previsible processes12 12 a process K w( t, x) is said to be a Borel previsible function or process if the process t ® K w( t, x) is a previsible function for fixed x and the function x ® K w( t, x) is Borel-measurable for fixed t. respectively. Suppose that
and K > 0, K(t,0) = 1 "t Î 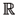 . Let k(t, x) be another Borel previsible process such that
. Let k(t, x) be another Borel previsible process such that
Define a process
t by
then 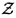 is a local martingale with
is a local martingale with 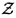 0 = 1 and
0 = 1 and 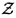 is positive if and only if K > 0.
is positive if and only if K > 0.
Proof From the fact
t 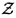 t =
t = 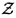 t( K(t, DNt) 1)
t( K(t, DNt) 1)
and applying Itô's formula and ( 14), we can obtain:
This expression is a local martingale.
Teorem 1 Let Q be a measure which is absolutely continuous with respect to P on
T. Then
where 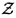 is as in the lemma 1, for some R, K and k for which E
is as in the lemma 1, for some R, K and k for which E
is a Brownian Motion and the process Nt is a quadratic pure jump process with compensator measure given by dt (dx) with
(dx) with
 (dx) = K(t, x)G(dx)
(dx) = K(t, x)G(dx)
and constant part given by
Then under Q the process Nt can be represented as
with
This process is a Q-martingale and it is easy to see that D = DMt. Now let
= DMt. Now let
be the discounted price process. Replacing the processes Wt and Mt in the equation (15) by their respective Q-versions, we obtain
A necessary and sufficient condition for  be a Q-martingale is the existence of R and K > 0 a.s. for which:
be a Q-martingale is the existence of R and K > 0 a.s. for which:
and E
t = 1, "t > 0. Since the process
is a Q-martingale. Now we can state the following
Theorem 2If there exist R and K > 0 for which E
t = 1 "t and the market price of risk is given by
Then the market
is arbitrage free.ProofTake a tame portfolio p and suppose that P(Mp(T) > 0) = 1, by definition we have
With equation (13) and (19) we obtain
Now using (16) and (17)
We have that Mp is a Q- local martingale bounded from below, since p is tame, then a supermartingale. Hence
EQMp(T) < 0
then Q (Mp(T) > 0) = 0, so there are not arbitrage opportunities.
From these result we know that our market is arbitrage free. Now we can introduce the investor problem.
4 Optimization Problem
In this section we formalize the individual problem of the investor, give some definitions and finally we present the main result.
Definition 4A pair (p,C) of portfolio consumption process is called admissible for the initial capital x > 0. If
The class of all such pairs will be denoted by  (x).
(x).
Now take any equivalent martingale measure Q and define the following state price density:
where
using (5) and the generalized Itô's lemma for F(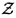 (t), g(t)X(t)) =
(t), g(t)X(t)) =  (t) X(t), we obtain:
(t) X(t), we obtain:
Now with the decomposition (13), we obtain
d( (t)X(t)) =
(t)X(t)) =  (t)dC(t) +
(t)dC(t) +  (t)p(t)s(t)[cdW (t) + dM(t)]
(t)p(t)s(t)[cdW (t) + dM(t)]
+ g(t) X(t)d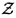 (t) + dD(t)
(t) + dD(t)
where D(t) is given by
In order to formulate our optimization problem we need the concept of utility function.
Definition 5We say that a function u:(0, ¥) ® R is a utility function if it is strictly increasing, strictly concave, continuously differentiable and
Examples of utility function are u(x) = log x and u(x) =  ,d Î (¥, 1)0.
,d Î (¥, 1)0.
We will denote by I(·) the inverse of the derivative u¢(·), both these functions are continuous, strictly decreasing, and map (0, ¥) onto itself with I(0+) = u¢(0+) = ¥, I(¥) = u¢(¥) = 0. We shall consider also de convex dual
Of u(·): a convex decreasing function, continuously differentiable on (0, ¥) and satisfies
Remarks on Utility Functions
-
Observe that (23) is the usual Inada's condition.
-
Negative wealth is not allowed to consider utilities that are economically relevant, as is the case of the u(x) = ln(x). But, we could take u(0) = ¥ and make u:[0, ¥) ® RÈ{¥}
-
In general we must have that marginal utility from consumption tends to infinite when wealth tends to the infimum of its allowed values.
Now consider an small investor who has an initial capital x > 0, and he wants to choose a portfolio p(·) and consumption processes {c(t), 0 < t < T} in order to maximize his expected utility from the terminal wealth Xx,p,C(T) and from consumption.
Given the utility functions g and u(t, ·), as in the above definition, we define the following classes:
remember f(x) = max f(x), 0.
Then our small investor will have to maximize the expected utility from consumption and terminal wealth over the following class:
The value function will be
Now to solve this optimization problem consider, in the context of the market model  described before, a contingent claim 13
13
A contingent claim x is a random variable
Tmeasurable.
x and a consumption process C that satisfy
described before, a contingent claim 13
13
A contingent claim x is a random variable
Tmeasurable.
x and a consumption process C that satisfy
Then if there exist a portfolio process p(·), such that (p, C) Î  (x) and Xx,p,C(T) = x; we could conclude that the optimal problem is in some sense equivalent to the following problem:
(x) and Xx,p,C(T) = x; we could conclude that the optimal problem is in some sense equivalent to the following problem:
over all pairs (x, c) of contingent claims and consumption rate process that satisfy the constraint (29) .
Now with y > 0 (Lagrange multiplier) and with (24):
the equality holds if and only if
then in the constraint (29), we define
and if we consider x Î (0, ¥) that is  (y) < ¥, "0 < y < ¥. This function maps (0, ¥) onto itself and is continuous, strictly decreasing with
(y) < ¥, "0 < y < ¥. This function maps (0, ¥) onto itself and is continuous, strictly decreasing with
If we denote by  (·) =
(·) =  (·). Then the lagrange multiplier y > 0 is uniquely determined by
(·). Then the lagrange multiplier y > 0 is uniquely determined by
y =  (x)
(x)
Now we can state the main result
Theorem 3Suppose x Î (0, ¥) and  (x) < ¥, "x Î (0, ¥) For any x > 0, consider the optimization problem with value function
(x) < ¥, "x Î (0, ¥) For any x > 0, consider the optimization problem with value function  (x) as in (??) and define x
(x) as in (??) and define x
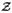 (·) as in (31). Then if
(·) as in (31). Then if
a) there is a portfolio process p
(·) such that (p
, C
) Î
(x) and
b) the process Dt is a Local martingale and D0 = 0.
Then (p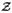 , c
, c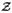 ) are the solutions of the optimal problem and the value function is given by
) are the solutions of the optimal problem and the value function is given by
where
and the convex dual of  (·) is
(·) is
Proof By construction x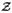 and c
and c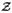 satisfy (29) and using the following inequality
satisfy (29) and using the following inequality
f (If(y)) > f (x) + y[If (y) x]
for every utility function f, we obtain
therefore
Since EH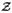 (t) < erT,0 < t < T, where r = sup0 < t < Tr(t) < ¥ and by (a) we have that there exist a portfolio process p
(t) < erT,0 < t < T, where r = sup0 < t < Tr(t) < ¥ and by (a) we have that there exist a portfolio process p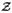 with (p
with (p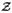 , C
, C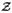 ) Î
) Î  (x) (also in
(x) (also in  0(x) thanks to (34)) and
0(x) thanks to (34)) and  a.s.).
a.s.).
Now take an arbitrary x > 0, (p, C) Î  0(x) and y > 0 from (b) we have that the following process is a bounded (from below) local martingale:
0(x) and y > 0 from (b) we have that the following process is a bounded (from below) local martingale:
then a supermartingale and with (30) we have
where
in particular follows
VZ(x) < Q(y) + xy, "x > 0
hence
On the other hand the inequality (34) holds as equality if and only if y =  (x) and (p, c) = (p
(x) and (p, c) = (p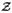 , c
, c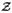 ) then
) then
now
and also
For every y > 0, and in conjunction with (35) we obtain Q(y) =  (y), "y > 0.
(y), "y > 0.
Remarks on the Assumptions
-
Assumption (a) is necessary and sufficient for the optimality of consumption. For the existence of the portfolio financing this optimal consumption we need to solve the following equation:
-
Assumption (b) is a sufficient condition which allow us to control the jumps on wealth and depending on the process Y considered, it can be easy verified as we will see in section 6 with an example. Condition D0 = 0 is just to simplify the proof. We can prove the same with D0¹ 0.
As we have seen in section 3, we obtained a characterization of the EMM. But it can be argued that choosing an EMM can be a hard task to solve, for these reason we show how to choose an EMM in the following section.
5 Choosing a Measure
There exists some approaches to choose one EMM, we concentrate our attention in the approach introduced by Gerber and Shiu (1994), define the new probability
where j(q) = EeqY1. When the stock price process has constant coefficients, Gerber and Shiu (1994) prove that for a given constant r it is possible to find a solution q of the following:
Then we can verify that the process  = ertPt is a martingale under Pq,i.e. PqÎ
= ertPt is a martingale under Pq,i.e. PqÎ  (set of EMM). Moreover the process is a Lévy Process under this probability and is called the Esscher transform14
14
For more details on Esscher transforms see Buhlmann et al. (1996)
of the original process. In our model we consider time dependent functions, then we consider the generalized Esscher Transform:
(set of EMM). Moreover the process is a Lévy Process under this probability and is called the Esscher transform14
14
For more details on Esscher transforms see Buhlmann et al. (1996)
of the original process. In our model we consider time dependent functions, then we consider the generalized Esscher Transform:
Now we can choose qs in order to satisfy equation (18), since this is the case of K(s, x) = exp(qsx), k(s, x) = qsx and Rs = cqs. In fact with these expressions we obtain
It easy to verify that this equation has an unique solution for which j(qs) < ¥ and qsÎ (b1, b2) "s. Then we can get a EMM, and important fact of this measure is that this is the measure of minimum relative entropy with respect to P, to see this remember the definition of entropy:
Where Q is any absolutely continuous measure with respect to P, with lemma 1 we have
where Q depends on the choice of K and R, and these functions have to satisfy equation (18). We can show 15 15 See Chan (1999) that this minimum is obtained when K = exp (xsl) and R = csl, where l is the lagrange multiplier associated to the constraint (18), this can justify the choice of the measure associated to q = sl.
6 Example
Take s = r = c = 1 and r = 0. Now assume that  , where Ni is a Poisson process with rate 1, so:
, where Ni is a Poisson process with rate 1, so:
-
G =

-
a = ENt = 0
Now we choose k(x) =  and K(x) = 1 k(x), replacing in condition (18) we obtain Rs = -
and K(x) = 1 k(x), replacing in condition (18) we obtain Rs = - , from the fact that DNs = 0, we have
, from the fact that DNs = 0, we have
It is easy to verify that E
T = 1, in other words it is a EMM density. So we have find one EMM. Now we apply the approach presented in last section to find the EMM that minimize entropy: as s = 1, then q = l. We obtain the parameter q that satisfy equation (38):
reducing this expression, we have:
the solution of this equation is q*» 0,6626. In equation (5):
we have also Yt = Wt + Nt and
where the first equality is due to the independence of Wt and N(t), the second is due to the fact that N1(t) and N2(t) are independent and identically distributed, and the third is the expected value of a Log-normal variable. From here we have
and this measure is obtained when K(s, x) = e0,6626x, k(s, x) = -0,6626x and Rs = 0,6626.
Now as Nt and Wt are martingales condition (b) in the main theorem is satisfied. Then if we take u(t, x) = g(x) = log(x), then Iu(x) = Ig(x) =  and
and
but
then y =  and
and
So depending on the state price density, i.e., on the EMM we choose, we have the path of the optimal policies. More precisely, if we desire to choose the EMM closest to P in terms of its information contents, since P contains information about the behavior of the market, we have to choose the EMM given by (39).16 16 For more details on how to construct EMM with different types of Lévy processes see Fajardo (2003).
7 Conclusions
In this paper we studied the optimal investment and consumption problem assuming that the risky asset is driven by a geometric Lévy process which allow us to obtain more realistic results. Another important issue addressed in this paper is the characterization of the EMM in a Lévy market and how to choose one of them using a minimal entropy criteria.
An important and difficult issue not considered in the paper is the availability of the portfolio processes, since many of the market models considered in the paper can be incomplete, we need to ensure that the financing portfolio is available in the market. For a discussion on this type of problem see Cvitani and Karatzas (1992).. Also from the existence of EMM we obtained the arbitrage free economies, with this in mind some equilibrium analysis in continuous time can be done.
and Karatzas (1992).. Also from the existence of EMM we obtained the arbitrage free economies, with this in mind some equilibrium analysis in continuous time can be done.
This paper was received in Nov. 2002 and approved in Feb. 2003.
- Benth, F. E., Karlsen, K. H., & Reikvam, K, . (2001). Optimal portfolio selection with consumption and nonlinear integro-differential equations with gradient constraints: A viscosity solution approach. Finance and Stochastics, (5):275303.
- Buhlmann, H., Delbaen, F., Embrechts, P., & Shirjaev, A. (1996). No-arbitrage, change of measure and conditional esscher transforms. CWI Quaterly, (9):291317.
- Chan, T. (1999). Pricing contingent claims on stocks driven by Lévy processes. Annals of Applied Probability, 9(2):504528.
- Cvitanic, J. & Karatzas, I. (1992). Convex duality in constrained portfolio optimization. Annals of Applied Probability, (2):767818.
- Eberlein, E. & Jacod, J. (1997). Hyperbolic distributions in finance. Finance and Stochastics, (1):281299.
- Fajardo, J. (2000). Optimal consumption and investment with hyperbolic Lévy motion. Brazilian Review of Econometrics, 20(1):2754.
- Fajardo, J. (2003). Equivalent martingale measures and Lévy processes. Working paper IBMEC.
- Gerber, H. & Shiu, E. (1994). Option pricing by esscher-transform. Transactions of the Society of Actuaries, 46:99191.
- Jacod, J. & Shiryaev, A. N. (1987). Limit Theorems for Stochastic Processes Springer-Verlag, New York.
- Karatzas, I. & Shreve, S. E. (1998). Methods of Mathematical Finance Springer-Verlag, New York.
- Kramkov, D. O. & Schachermayer, W. (1999). The asymptotic elasticity of utility functions and optimal investment in incomplete markets. Annals of Applied Probability, 11(3):904950.
- Merton, R. C. (1971). Optimum consumption and portfolio rules in a continuous-time model. Journal of Economic Theory, (3):373{413.
- Rydberg, T. (1997). Why financial data are interesting to statisticians. Centre for Analytical Finance, Aarhus University. Working Paper 5.
- Sato, K.-I. (1999). Lévy Processes and Infinitely Divisible Distributions Cambridge University Press, Cambridge.
- Shiryaev, A. N. (1999). Essential of Stochastic Finance: Facts, Models and Theory World Scientific Pub. Co.
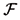 (
(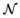 ), where
), where 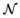 = {
= {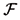 with
with 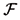 (
(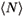 . Remember that
. Remember that 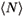 is the process such that (
is the process such that (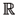 ×
×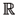 \0,
\0, Publication Dates
-
Publication in this collection
14 June 2004 -
Date of issue
Dec 2003
History
-
Received
Nov 2002 -
Accepted
Feb 2003















































































