On the similarity transformations in second quantized fermion-boson interacting hamiltonian and the BCS theory

Abstracts

A similarity transformation is an equivalence relation between square matrices which preserves determinant, trace and eigenvalues, playing a key role in quantum mechanics in simplifying complex hamiltonian systems and improving analytical results attainable from the use of perturbation theory. As a prototypical example, the conventional BCS theory of superconductivity is usually derived from a similarity transformation of the original electron-phonon hamiltonian, written in second quantized version. Here we discuss the general method for writing the similarity transformation operator in second quantized form, allowing one to recast a hamiltonian describing an interacting fermion-boson system into an effective theory in which only the desired degrees of freedom are kept after the transformation.

Keywords:
fermion-boson systems; similarity transformation; second quantization; superconductivity

Uma transformação de similaridade é uma relação de equivalência entre matrizes quadradas que preserva o determinante, traço e autovalores da matriz, tendo papel fundamental na mecânica quântica para fins de simplificar sistemas hamiltonianos muito complexos, o que permite melhorar de forma significativa as soluções analíticas no uso de teoria de perturbações. Um exemplo prototípico desse tipo é a teoria BCS para a supercondutividade convencional, derivada de uma transformação de similaridade da interação elétron-fônon original, escrita na forma de segunda quantização. Nesse trabalho, discutimos o método geral para escrever o operador de transformação de similaridade na forma de segunda quantização, permitindo reescrever o hamiltoniano de interação entre férmions e bósons, obtendo uma teoria efetiva em que somente os graus de liberdade de interesse são retidos depois da transformação.

Palavras-chave:
sistemas férmion-bóson; transformações de similaridade; segunda quantização; supercondutividade

1. Introduction

There is little room for controversy in stating that fermion-boson interacting systems are among the most general problems in physics, since they can be used to describe almost everything in the real world, at least at a quantum-mechanical level. For instance, in the standard model of elementary particles the interaction between fermions(electrons, neutrinos and quarks) are mediated by the so-called gauge bosons (photons, gluons and so on) [¹–³]. In cavity quantum electrodynamics problems, fermion states in a multilevel system are coupled via photons, leading to a large class of problems that can be mapped to the Jaynes-Cummings models [⁴,⁵]. Electronic transport properties are affected by electron-phonon coupling in solids, leading to the phenomenon of superconductivity in many materials [⁶–⁸]. Despite the apparent simplicity of fermion-boson models when written in second quantization formalism, the vast majority of these problems are not solvable in an exact manner and, therefore, demand clever methods and mathematical tricks in order to obtain an analytically tractable perturbation scheme, allowing one to predict meaningful physical results.

As a matter of fact, the term second quantization is synonymous to quantum field theory, which naturally describes many-body problems and can be represented in two very dissimilar but otherwise equivalent ways, to be known [¹–³,⁹,¹⁰]: i) Feynman path integral formulation, based on “sum over histories”, which is beyond the scope of the present contribution and ii) canonical quantization formalism, firmly grounded on the use of the so-called creation and annihilation operator algebra. While Feynman formalism deals with gaussian integration gymnastics [¹⁰], one of the most important mathematical tool for the canonical formalism is the similarity transformation of the hamiltonian. A similarity transformation is an equivalence relation between square matrices which preserves all the relevant information in quantum mechanics, i.e., matrix determinant, trace and eigenvalues. It can be used to promote a change of basis or a symmetry transformation [¹¹,¹²], leading to an equivalent hamiltonian, in which the terms too complicated to be dealt with are completely eliminated, at least in first order of a perturbation series expansion, thusly simplifying the problem. In the canonical formalism, the conventional BCS theory of superconductivity is usually derived from a similarity transformation of the original electron-phonon hamiltonian [¹²].

In the present contribution, we discuss the general method for writing similarity transformation operators in second quantized form, allowing one to recast a hamiltonian describing an interacting fermion-boson system into an effective theory, in which only the desired degrees of freedom are kept after the transformation. The proposed rule of thumb is applied to the problem of electron-phonon interactions in obtaining the BCS theory of superconductivity.

The content of this paper is organized in the following way: in the next Section we will introduce and briefly discuss the fermion-boson general problem in the canonical formalism. In Section 3 the general method for obtaining similarity transformation operators in second-quantized version is presented. Section 4 brings the application of the method to the BCS theory of superconductivity and, finally, in the last Section a few conclusions and remarks are added.

2. The general form of fermion-boson interacting hamiltonians

Our primary interest is in the problem of fermion-boson interacting systems, described by the following general hamiltonian:

(1)

where E_i are the energy eigenstates of the fermionic degrees of freedom with a set of quantum numbers labeled by the index i, n and i-th quantum state, while

(2)

(3)

where {A,B} = AB + BA is the anti-commutator for any two operators A and B, δ_ij is the Kronecker delta function, yielding 1(0) for i = j(i≠j). By contrast, bosonic operators obey a commuting algebra, explicitly written below:

(4)

(5)

where [A,B] = AB − BA is the commutator of A and B. The number operators are defined as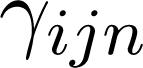 is the fermion-boson coupling parameter, depending on the bosonic quantum number, 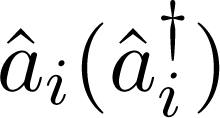is a bosonic annihilation (creation) operator. Fermionic operators must obey the following anti-commuting algebra: 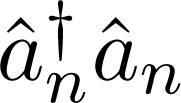for fermions and bosons, respectively. 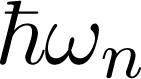is the energy of a bosonic state with quantum numbers labeled by 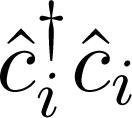and 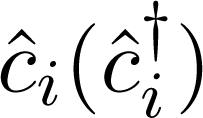is a fermionic operator which annihilates (creates) a fermion in the

In the above hamiltonian, the first term, is related to the fermion system alone, whose energies are supposed to be exactly known. The second term, j-th state to the i-th state by absorbing a boson with quantum number n. The last term , , is related to the energy of the bosonic degrees of freedom, and it conserves the boson number, since it is diagonal in the number representation. The last terms represent the fermion-boson interaction, which permits non-conservation of the boson number. For instance, the term represents the fermion transition with boson emission. In either case, it is clear that the total boson number is not preserved, i.e., states with distinct boson number are coupled due to the interaction. It is usually the case that the fermion-boson interaction is weak and can be treated as a small perturbation, which is known as the weak coupling limit. represents the transition of the fermion from the

3. The general method of similarity transformation

As the starting point, consider the following hamiltonian:

(6)

where ². If necessary, the next leading order can also be eliminated by continuing the transformation procedure to be described below. Elimination of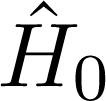

(7)

are known, and therefore we want to eliminate the perturbation term 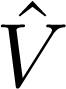to first order in λ is accomplished by applying a similarity transformation to , as follows: 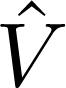is the perturbation, usually responsible for the interactions. The parameter λ is used to control the intensity of the perturbation term. For λ → 0 interactions are absent, but for small λ perturbation theory is generally valid, while for λ → ∞ the system is dominated by the interaction term and perturbation theory breaks down. In order to solve the problem in the weak coupling limit (λ < 1), we assume the eigenstates of , at least to first order in the coupling parameter λ. This way, in the transformed hamiltonian the perturbation will appear only at the next leading order, which is λ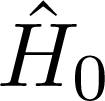 is an unperturbed hamiltonian and

Notice that, since the hamiltonian must be hermitian in quantum mechanics and e^Ŝ must be an unitary operator, the matrix Ŝ must obey the relation Ŝ^† = −Ŝ. Expanding the above equation in Taylor series yields:

(8)

which can be promptly recast into the following form:

(9)

After inserting (6) into the above equation, we get:

(10)

Going further, the term

(11)

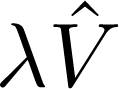can be eliminated from the problem to first order in λ by making:

Looking at the above equation, it is clear that Ŝ will depend linearly on λ. Using the set of

(12)

we can straightforwardly solve the equation (11) for the operator Ŝ, being the result: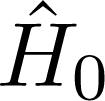

(13)

eigenstates, satisfying the eigenvalue equation below,

Making use of (11), we can rewrite the transformed hamiltonian

(14)

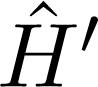in the following way:

Now the perturbation is in the term ². It must be pointed out that the quantum state of Ĥ satisfying the equation E., but it possesses the same energy eigenvalue , which depends on λ is also transformed,

Next, we turn our attention to the form of the transformation matrix Ŝ given by equation (13) and its connection to the fermion-boson problem. The term |m⟩⟨n| can be interpreted as an operator which annihilates the initial state |n⟩ and creates the final state |m⟩. It is weighted by the matrix element E_m − E_n) between final and initial states. It is our aim to write Ŝ as a second-quantized operator, observing the form of the perturbation operator m⟩⟨n| in (13) by creation and annihilation operators exactly in the same order as they appear in the operator E_m − E_n can be easily calculated considering the total number of particles appearing in the final and initial states. Let us consider the fermion-boson hamiltonian (1) written as follows:

(15)

(16)

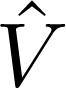divided by the energy difference (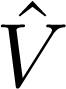. To do that, we must replace |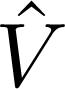. The energy difference 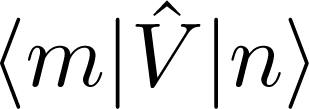of the perturbation operator

Taking a closer look at the term n-th state and a fermion in the j-th state, creating a fermion in the i-th final state. Therefore, the initial energy of the fermion-boson system is E₀ + E_j + ℏω_n and the final energy is E₀ + E_i, where E₀ is the sum of all other energies in the system, not involved in this specific interaction process. The energy difference between final and initial states will be given by E_i − E_j − ℏω_n. In writing down the matrix Ŝ, this term will show up as Ŝ, as follows: i) write down the perturbation operator Ŝ and ii) divide each term by the energy difference between final and initial states produced by that specific term. It is easy to see that for the perturbation (16) the transformation matrix Ŝ will be given by:

(17)

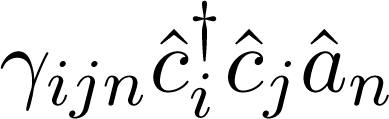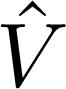in for 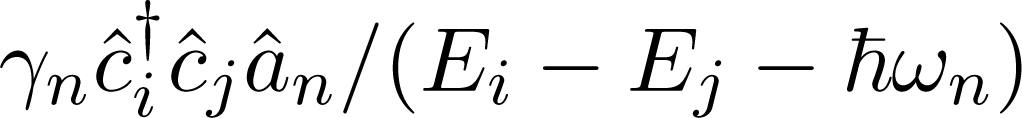. Taking into consideration the above discussion, we prescribe, as a rule of thumb, a direct method for obtaining 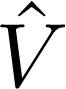, we know that it will annihilate a boson in the

The interested reader is encouraged to demonstrate explicitly that the above expression for Ŝ exactly solvesequation (11), provided the knowledge of the fermionic and bosonic relations (2)-(5and the Hamiltonian (6), conveniently splitted as (15) and (16).

Notice that the prescribed method for writing down Ŝ works for very general situations. For the sake of simplicity, consider the boson hamiltonian below:

(18)

Indeed, the above problem is a trivial one, since it can be exactly diagonalized by the replacement Ŝ:

(19)

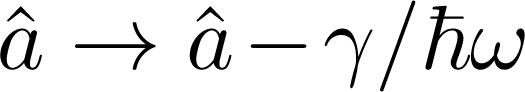, leading to 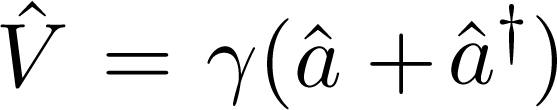. Following the above mentioned prescription, we write down the matrix 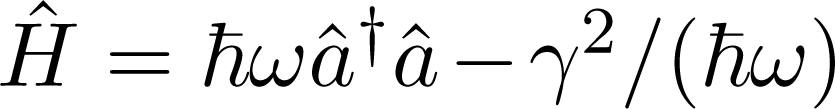, but we will use the similarity transformation method in order to eliminate the perturbation

It is straightforward to show that the energy difference between final and initial state due to the term γâ is − ℏω, since initially there are n bosons of energy ℏω and, after annihilation of one boson we are left with n − 1 bosons, leading to an energy deficit of ℏω. Inserting (18) and (19) into (14) and making use of

(20)

which is the exact result in this particular case.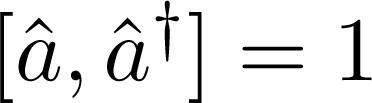 we obtain:

In the next Section we will use the method described here to obtain the BCS hamiltonian describing conventional superconductivity.

4. The conventional BCS superconductivity theory

The BCS theory successfully explains the conventional superconductivity of materials, by considering attractive electron-electron interactions mediated by the exchange of virtual phonons(the quantized excitations of lattice vibrations), which leads to the formation of the so-called Cooper pairs, a bound state of electrons in momentum space. The starting point of the BCS theory is the electron-phonon Hamiltonian [¹²]:

(21)

(22)

where ℏk (and spin σ =↑, ↓, which is being omitted) and energy ℏq and energy ℏω_q, the parameter D_q is the electron-phonon coupling and depends only on the phonon momentum ℏq, not on the electronic momentum ℏk, in the present case. It is left as an exercise to show that the requirement of hermiticity of the hamiltonian leads to the condition Ŝ:

(23)

where we have used the fact that ω_q = ω−_q. Going further, we need to determine Ĥ′. The result is:

(24)

where we defined the terms below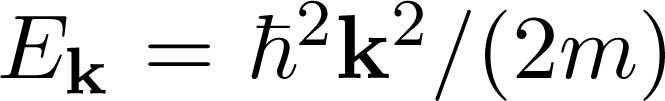

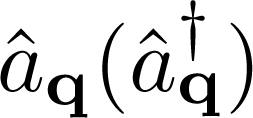(25)

(26)

(27)

(28)

, annihilates (creates) a phonon (boson) with momentum 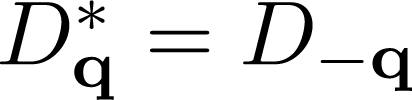. Using the prescription described in the previous Section we can easily write down the transformation matrix 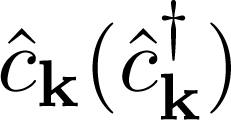annihilates(creates) an electron(fermion) with momentum 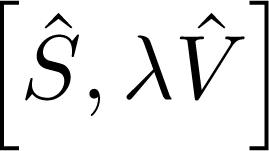in order to obtain

As a final step, we want to retain only fermionic degrees of freedom by tracing out the phonon variables. It can be done by averaging phonon operators in the canonical ensemble, for which the density matrix is written as A₁ and A₄ vanish by virtue of the trace properties A₃ and A₄ are of the form below:

(29)

where i = k + q, j = k and so on. The commutator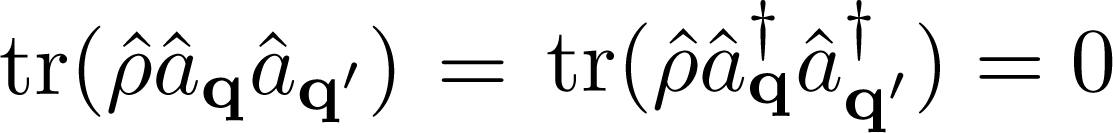

(30)

. The remaining terms must be carefully calculated, taking into account that in the canonical ensemble 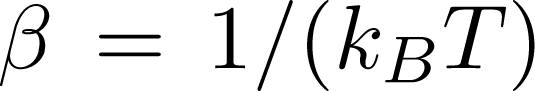is the reciprocal of the temperature. Notice that the terms 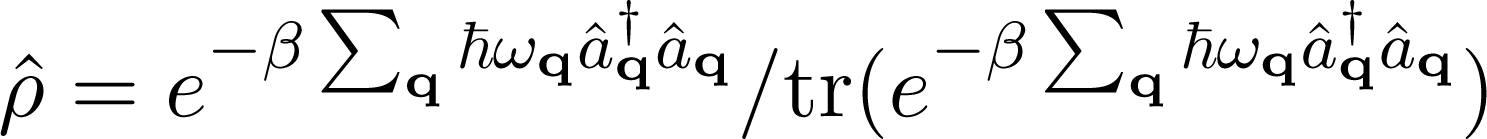, where 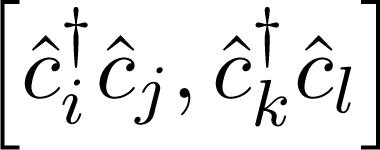can be handled with the help of the following identity: 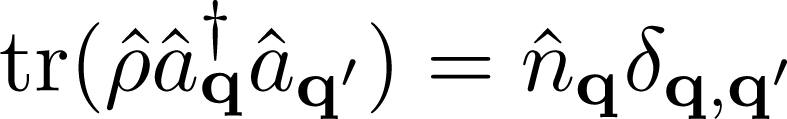for phonon operators. The commutators appearing in

The last steps towards the BCS hamiltonian are left as an exercise, but the result

(31)

where

(32)

T = 0 the phonon number vanishes for any q and the electron-phonon interactions does not produce any effect on the electron energy, i.e., 31). Using the fermionic relations one can rewrite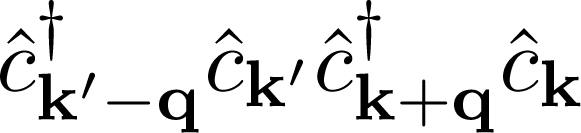

(33)

as follows: 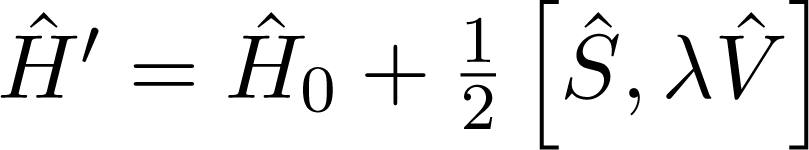, after averaging over the phonon operators, is shown below: 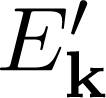is the electron energy, corrected by phonon interactions: 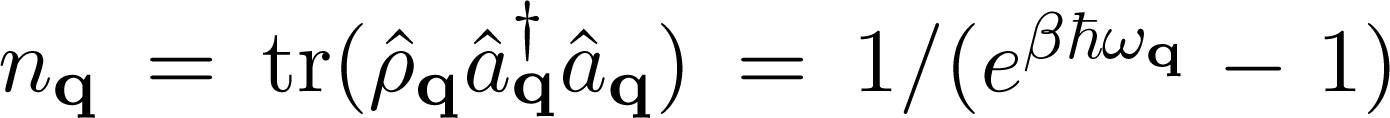is the phonon number. At 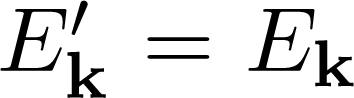, but for higher temperatures it deviates from the parabolic energy-momentum dispersion relation, which is characteristic of non-relativistic free particles. Now we will put the effective electron-electron interaction, by making some rearrangements in the last term in (

Inserting this last result into equation (31) one can show that:

(34)

where

(35)

and ¹³], who shared the Nobel Prize in 1972 for their achievements in the theory of superconductivity, The famous result is given below [⁸, ¹²–¹⁴]:

(36)

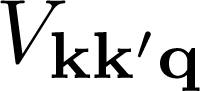is the effective coupling resulting from the (virtual) phonon exchange, firstly derived by J. Bardeen, L.N. Cooper and J.R. Schrieffer [ 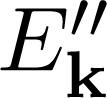is the re-corrected electron energy, given by:

We point out that it is usual to labeljust as V_kqin the current literature [⁸,¹²,¹⁴]. Notice that for V_kq becomes negative, meaning that the interaction is attractive, which is the key ingredient for the formation of Cooper pairs, a bound state of two electrons in momentum space, in the conventional BCS theory of superconductivity. Further discussions can be found in classical textbooks on condensed matter theory [⁶–⁸,¹²,¹⁴]. the coupling

5. Conclusion

In summary, in the present manuscript we presented a brief introduction to general fermion-boson hamiltonians, in which boson number is not conserved due to the fermion-boson interactions, thus complicating the search for exact solutions in closed analytical form, demanding a perturbation scheme to deal with the mathematical problem. One of the most useful methods is based on similarity transformation of the original hamiltonian, eliminating the interactions to first order in the coupling constant. A rule of thumb for obtaining the similarity transformation operator in second-quantized form is presented and applied to the problem of BCS theory of superconductivity.

Acknowledgements

C.A. Dartora would like to thank the Brazilian agency CNPq for partial financial support through grant and scholarship CNPq 471521/2013-2 and 301894/2014-0. The authors thank the anonymous referee for valuable contributions for the final version of this work.

References

• ^[1]
  S. Weinberg, The Quantum Teory of Fields (Cambridge University Press, Cambridge, 1996), v. I and v. II, and references therein.
• ^[2]
  L.H. Ryder, Quantum Field Theory, (Cambridge University Press, Cambridge, 1996), 2nd ed.
• ^[3]
  M.E. Peskin and D.V. Schroeder, An Introduction To Quantum Field Theory (Addison-Wesley Publishing Company, Boston, 1995), 1st ed.
• ^[4]
  E.T. Jaynes and F.W. Cummings, Proc. IEEE 51, 89 (1963).
• ^[5]
  F.W. Cummings, Phys. Rev. 140, A1051 (1965).
• ^[6]
  N.W. Ashcroft and N.D. Mermin, Solid State Physics (Cengage Learning, Boston, 1976), 1st ed.
• ^[7]
  C. Kittel, Introduction to Solid State Physics (John Wiley and Sons, New York, 2004), 8th ed.
• ^[8]
  O. Matelung, Introduction to Solid State Physics (Springer-Verlag, Berlin, 1996), 3rd ed.
• ^[9]
  W. Greiner and J. Reinhardt, Field Quantization (Springer-Verlag, Berlin, 1996), 1st ed.
• ^[10]
  A. Altland and B. Simons, Condensed Matter Field Theory (Cambridge University Press, Cambridge, 2010), 2nd ed.
• ^[11]
  M. Tinkham, Group Theory and Quantum Mechanics (Dover Publications, New York, 2003), under permission of McGraw-Hill.
• ^[12]
  C. Kittel, Quantum Theory of Solids (John Wiley and Sons, New York, 1963), 1st ed.
• ^[13]
  J. Bardeen, L.N. Cooper and J.R. Schrieffer, Physical Review 108, 1175 (1957).
• ^[14]
  W. Jones and N.H. March, Theoretical Solid State Physics, Volume 2, Non-Equilibrium and Disorder (Dover Edition, New York, 1985).

Publication Dates

• Publication in this collection
  Sept 2016

History

• Received
  28 Dec 2015
• Reviewed
  04 Apr 2016
• Accepted
  14 Apr 2016