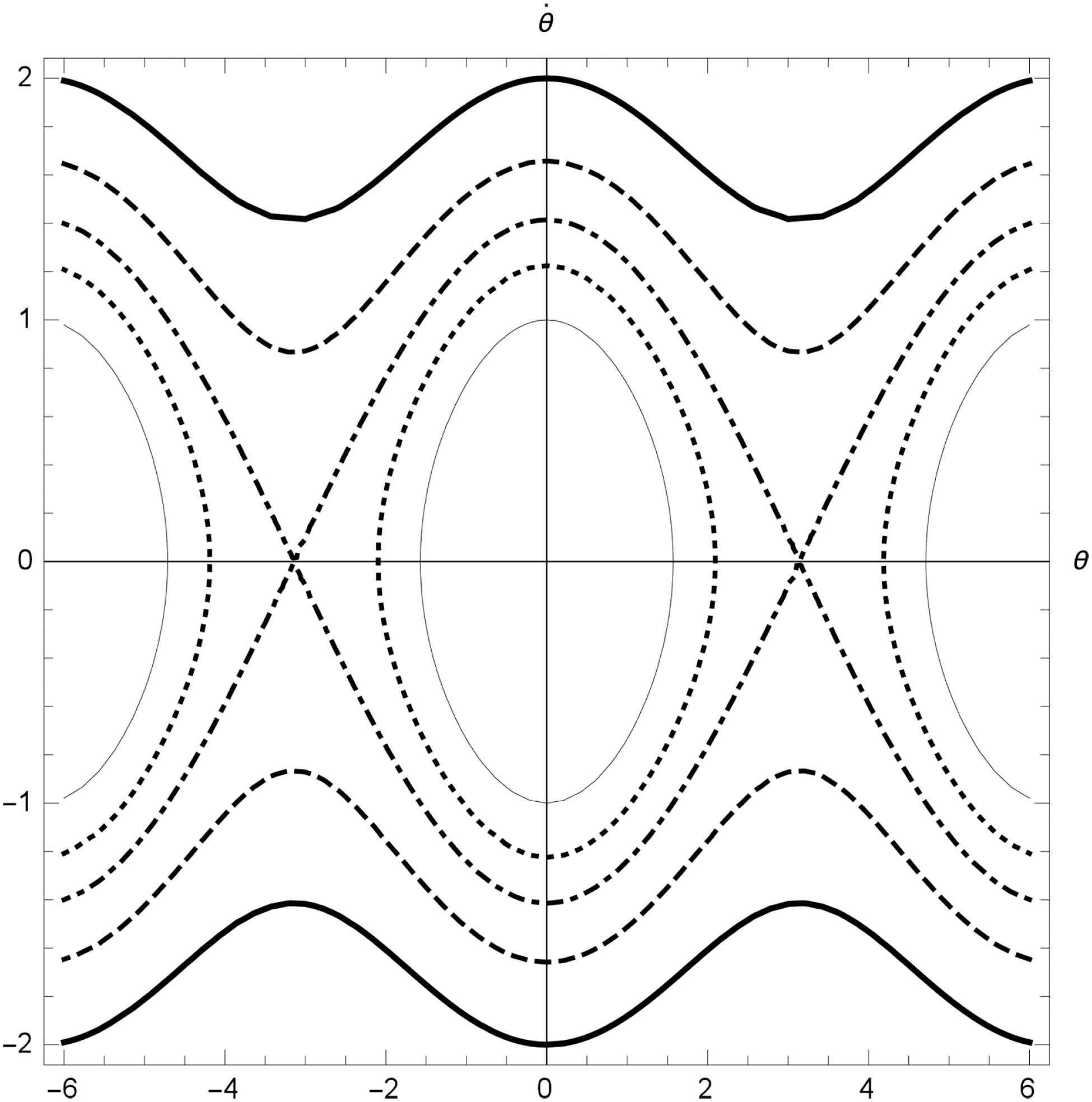
In this report we review some of the most paradigmatic nonlinear systems and unveil some of their suprising interconnections. The problems of interest, described mathematically by the equations of sine-Gordon, Toda and KdV, generalize well known physical models, the simple pendulum, the mass on a spring and the linear waves, respectively. After discussing the differences arising from the presence of nonlinearities in the models, we clarify how the systems presented are related to each other, indicating existence of a family of equations sharing integrability properties. We show how the KdV equation can be conveniently discretized in order to preserve important properties. Besides presenting the close connections this equation has with respect to the Toda lattice and the sine-Gordon equation, we also investigate other procedures capable of generating a discrete integrable system from the KdV model, as the Hirota discretization.
Keywords:
KdV; Sine-Gordon; Toda Lattice