Behavior prediction models and control charts for safety control of concrete dams

Modelos de previsão de comportamento e gráficos de controle para verificação de segurança de barragens de concreto

Abstracts

Um estudo para a melhoria dos procedimentos de auscultação de barragens de concreto é apresentado neste trabalho a partir do desenvolvimento de modelos de previsão de comportamento baseados em regressão múltipla e gráficos de controle. Tomou-se como exemplo de aplicação a série histórica dos deslocamentos da crista do bloco de concreto TA-2 da UHE Tucuruí, maior usina hidroelétrica genuinamente brasileira. A metodologia apresentada foi capaz de gerar um modelo de previsão de comportamento aderente aos deslocamentos medidos. Dois tipos de gráficos de controle foram testados, onde ambos identificaram a mudança de comportamento estrutural do bloco.

barragens de concreto; modelos de previsão; gráficos de controle; auscultação

Behavior prediction models and control charts for safety control of concrete dams

R. A. C. Lopes^I; E. P. Santos^II; L. A. C. M. Veloso^III

^IInstitute of Technology, Civil Engineering College, Universidade Federal do Pará, [e-mail], Rua Augusto Corrêa, Belém, Brazil

^IIInstitute of Technology, Computer Engineering College, Universidade Federal do Pará, [e-mail], Rua Augusto Corrêa, Belém, Brazil

^IIIInstitute of Technology, Civil Engineering College, Universidade Federal do Pará, [e-mail], Rua Augusto Corrêa, Belém, Brazil

ABSTRACT

This paper presents a study for improving measurement procedures on concrete dams based on the development of behavior prediction models using multiple regression and control charts. The series of displacements of the TA-2 concrete block crest of the Tucuruí Hydroelectric Power Plant, the largest Brazilian hydroelectric power plant, was taken as an example of application. The methodology that was used generated a behavior prediction model that is in good agreement with the measured displacements. Two types of control charts were tested, both of which identified the change in structural behavior of the block.

Keywords: concrete dams, prediction models, control charts, safety control.

1. Introduction

For many years, dams have acted as major engineering works to improve various sectors of our society or even introduce factors in a region that make the location more appropriate for people to remain in their places of origin.

Some of the main functions of dams include: flood control in areas near rivers, water storage and irrigation in areas with long periods of drought, containment of tailings from mining companies, recreation, and power generation.

Since the beginning of the Industrial Revolution, society has increasingly needed energy sources. As a result, the governments of several countries began to invest heavily in building dams, because they can generate large amounts of energy depending on the site where they are installed. Not only has the number of dams increased but their size has also increased, as is the case of the Itaipu concrete dam, built by Brazil in association with Paraguay. The dam is the largest operating hydroelectric facility in terms of annual generating capacity. The construction of this dam consumed approximately 28 million tons of concrete [1]. The concrete dam of Itaipu has maximum height of 196 meters from the crest to the foundation, and is 7,919 meters long.

Currently, there is a major concern in conducting a detailed assessment of the structural behavior of buildings. This is justified by the fact that many structures that are built nowadays are much larger than those built in the past, because they have an innovative structural arrangement or are even prone to exceptional actions, such as those structures erected in countries with strong seismicity.

In structural engineering, dams are among the structures that have been monitored for a long time and have a higher number of installed sensors - usually thousands, as is the case of the Tucuruí dam, in northern Brazil, which has about 2,800 sensors [2].

According to the Centro da Memória da Eletricidade no Brasil (Brazilian Center forElectric Power History) [3], the study of dam safety began in the United States around the 1950›s with the dam safety program of the Bureau of Reclamation, which established the recommendations on the matter after a review by the National Research Council›s Report. Such recommendations include installing field instruments that enable monitoring the structural behavior of dams and prioritize inspection of dams in high-risk sites.

The first analyses related to dam engineering focused on the determination of displacements, strains and stresses. With the advent of new sensors, it became possible to determine other structural behaviors, such as: determination of natural frequencies and vibration modes, allowing the comparison of numerical results with the measured data, which also allowed the online evolution of natural frequencies and early detection of structural deterioration and aging processes [4].

Because of the size of large dams, which are among the largest constructions in civil engineering, it became necessary to establish some methods to verify the safety conditions of this type of construction, since collapse of these structures brings about huge social, economic and environmental damages.

According to [5], the safety control of a dam comprises the environmental safety control, the hydraulic and operating safety control, and structural safety control. The procedures for assessing the safety of a dam along its life are called auscultation.

This paper uses predictive models based on multiple regression and control charts to predict magnitudes measured by typical instruments installed in concrete dams. Prediction models and control charts can be used by auscultation team technicians and engineers to assess structure behavior and to analyze the data measured, since the measured values are susceptible to errors that may occur during data collection or even due to instrument failure.

These new tools add a new parameter to be analyzed in relation to the structural safety control of dams, which in some cases takes into account only the comparison of the instrument-measured data against warning values usually established in the dam design stage.

As an object of study, we considered the direct pendulum installed on concrete block TA-2 of the Tucuruí Hydroelectric Power Plant, which is used to measure the displacements of the block crest.

2. Background

Because large dams are constructions that require high economic investments and play a key role in Brazil's energy plan, it is expected that special care will be in place for the building and maintenance of such constructions. Brazilian Law No. 12.334 [6], dated 20 September, 2010, establishes the National Dam Safety Policy, the goals of which, according to its article three, are as follows:

I - ensure compliance with dam safety standards in order to reduce the possibility of accidents and the consequences thereof;

II - regulate the safety actions to be taken in the planning, design, construction, first filling, operation, decommissioning, and future uses of dams throughout the country;

III - the people in charge of the dams are to promote safety monitoring and follow-up;

IV - create conditions for extending dam controls by the government, based on the supervision, guidance and correction of safety actions;

V - collect information that supports governmental management of dams;

VI - establish technical compliance that allows for evaluating the adequacy of those parameters established by the Government;

VII - develop a culture of dam safety and risk management.

Therefore, auscultation plans are put into practice when the constructions begin and are followed up throughout dam's life.

A considerable amount of research has been developed in Brazil and Portugal to develop dam behavior prediction models, especially based on multiple regression models, thus contributing to improving safety control procedures with direct reflex on the maintenance of said structures as well. Amongst such works, one can mention the research carried out at LNEC - the National Laboratory of Civil Engineering, in Portugal, [7] and [8] as well as several Brazilian contributions, such as those made by [9] and [10].

Based on well-adjusted behavior prediction models, the reading of the instruments should be close to the value estimated; otherwise, it is possible to investigate the cause of this discrepancy and, if necessary, employ timely preventive actions. The auscultation team may also count on the help of control charts, which allow for easy viewing when the dam is undergoing a change in behavior.

3. Auscultation

According to [11], although instrumentation does not provide the solution to all problems, when it is properly designed, installed and read, it can not only assess the safety conditions of a project throughout its phases, but also to verify the assumptions made in the design phase, making the construction works more economical. In the TA-2 block of the Tucuruí Hydroelectric Power Plant, the auscultation instruments installed include the direct pendulum, piezometers and triorthogonal joint gauges.

The readings provided by the instruments can describe dam behavior quite reliable. The data measured by the instruments may show if the structure is being acted in such a way that its design limits might be exceeded. Consequently, steps can be taken in order to bring the dam back to normal operating condition.

According to historical readings, it is possible to notice that some instruments begin to show anomalous readings over time. This often occurs because the instrument has suffered wear and fatigue, i.e., it has exceeded its useful life.

In the case of the HPP Tucuruí, the frequency of readings is set by EEGE (Eletronorte Geotechnical and Structures Management) [2].The frequency of readings varies for each instrument, and can be daily, weekly, biweekly, monthly, bimonthly, quarterly or every six months.

According to [8], in terms of structural behavior, assessment of safety conditions can be conducted by comparing the collected readings to the estimated values based on predictive behavior models. The results estimated by the prediction models can be taken as an indication of the behavior considered normal for the structure in the future.

The parameters set by the statistical models should be reevaluated at regular time intervals, as changes in behavior might occur due to changes in the characteristics of the structure or foundation. Because of these behavior changes, it becomes difficult to define normal and abnormal behavior, because according to [12], as quoted in [5], one can always make two types of errors: the first corresponds to a judgment of a false normality and the second corresponds to a false judgment of abnormality.

4. Methodology

4.1 Multiple regression

Multiple regression is used to develop an empirical model that associates a dependent variable Y to more than one independent variable. The model equation is as follows:

where:

n is the number of values for the historical series that was analyzed;

_i is the dependent variable (i = 1,2, ... n);

x_ik are the independent variables (k = 1, ... n);

β₀, β₁, β₂, ..., β_n are the regression coefficients;

Є_i is the random error.

Multiple regressions should provide a curve that has the best adherence possible to the observed data. According to [13], this adhesion can be obtained through the Least Squares Principle, which aims to reduce the sum of squared deviations between the desired values and the estimated values, as shown in equation [2]:

where f(β₀, β₁, ..., β_n) must be minimized with respect to β₀, β₁,..., β_n. The least squares estimates of β₀, β₁,..., β_n must satisfy:

By rearranging the equations and putting them in matrix notation, one obtains:

Where the i-th line of matrix X is formed by the vector [1 X_i1 X_i2 X_i3 ... X_in], which corresponds to variables that influence the response _i. Vector y corresponds to displacements toward the flow direction of block TA-2.

For the estimate of least squares, errors are assumed to be statistically independent, and to have zero mean and constant variance. If these conditions are met, the coefficients

₀,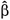 ₁, 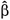₂, ..., 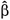_n can be considered unbiased estimators of the regression coefficients.

The adjustment of the model to the desired values is measured quantitatively by the coefficient of multiple determination, R². This coefficient measures the ability of the regression model to explain the variation of . R² values close or equal to 1 mean that there is good adherence between the model and the experimental data, while R² values close to zero mean that the model is not suitable for the prediction. The coefficient of multiple determination is obtained as follows:

where:

SQE is the quadratic sum of the error;

SQT is the total quadratic sum of the deviations;

is the mean of observations.

4.2 Selection of independent variables

The independent variables were chosen based on the correlation of each with the dependent variable and based on existing literature on dam behavior prediction models. The variables selected for the prediction models for displacement of the TA-2 concrete block are described below.

According to [5], the estimated effects E depend on two components, one of an elastic nature Er, formed by the portions related to hydrostatic pressure and temperature, and another of an inelastic nature Et, which represents the effect of creep over time. Thus, E is expressed as follows:

According to [8], the contribution from the upstream level is often represented by a polynomial function of the form:

where:

h is the upstream level in meters;

a₁, a₂,..., a₄ are adjustable parameters.

In the operation phase of the dam, the concrete temperature variations depend mainly on environmental temperature variations. According to [8], the annual influence of thermal effects on the concrete block can be represented by the sum of annual harmonic functions. The annual temperature function can be given by:

where:

t_d is the number of days elapsed from the beginning of the year until the date of observation in the same year;

b₁, b₂, b₃, b₄ are adjustable parameters.

According to [14], the effect of creep over time can be represented through the elements of a Dirichlet series, which has the form:

where:

t represents the number of days elapsed from the date of first observation;

c₁ and c₂ are adjustable parameters.

Considering that the displacement of the block crest is influenced by the variables mentioned above, the function used in the prediction has the following form:

Figures [1], ^[2] and ^[3] show the contribution of the upstream level, temperature and concrete creep in overall displacement of the dam crest.

4.3 Control chart

According to [15], the ultimate goal of the statistical process control is the elimination of variability in the process. Although it may not be possible to completely eliminate variability, the control chart helps to reduce it as much as possible.

The control charts very well describe what the statistical process control is all about. They are usually used for online monitoring and they make it possible to ascertain whether recent predictions are under control. When values exceed the limits set in the chart or when the analyzed variable is undergoing a behavior that may be considered nonrandom, it is necessary to detect and eliminate the cause of variability.

When a process involves more than one control variable, it is preferable to use control charts for model residuals. The control chart for the regression residuals allows for the analysis of the influence of more than one control variable on the dependent variable. Normalized residuals were used hereby since, according to [16], the standardized residuals are escalated so that their standard deviation is approximately equal to 1. Therefore, the major residuals will be more obvious as from the inspection of residual charts. The standardized residuals were obtained in the Student form, according to equation [13].

where

² is the mean square for the errors, calculated as follows:

where:

p is the number of independent variables;

h_ii is the i-th element of the diagonal of the matrix H and the variance of the adjusted value _i. Thus, it can be interpreted as the distance of points X_i in relation to the average of all points of X in the data set. The matrix H is usually called the hat matrix because it transforms the values observed by the auscultation instruments into a vector of estimated values . The matrix H is calculated as follows:

The control limits are selected on the basis of the value of the t distribution and based on the desired level of significance, which in this study was 95% for the +/- 1.96 limit and 99% for the +/- 3 limit. In this paper the control chart for the regression residuals was called Control Type I and is given by:

where:

LS is the upper control limit;

LC is the central control limit;

LI is the lower control limit;

α is the confidence level of the t distribution.

One of the problems with control charts using residuals is that at times it is difficult to interpret them, because they are not always a direct reference to the process. Pedrini [16] proposed the use of a regression control chart that takes into account the direct value of the observations corresponding to the dependent variables. In this study, this method was named Control Type II.

As can be seen from equation [19] to [21], the proposed method consists of a slight modification of the method presented earlier.

Note that the control limits are not straight lines, as in the method that uses standardized residuals, but curves that will vary according to the regression model.

4.4 Analysis of input variables

At first, the block crest displacement time series was observed in order to find reading trends or errors.

According to [5] several factors may contribute to the source of errors in measurements, such as the type of instrument, the reading unit, the reading method, and human intervention introduced by the operator's method.

To determine which values could affect the analysis, Cook's distance was used, which measures how much a value can interfere with the process. Cook's distance is calculated according to equation [22].

A value of indicates that the i-th point of analysis has some influence and should be investigated and, if necessary, eliminated from the series. Throughout the analysis, some values exceeded Cook's distance. After these values were eliminated, an improvement in the coefficient of multiple determination was noticed.

4.5 Analysis of results

Figure [4] shows the displacements measured by the direct pendulum, as well as the displacements calculated from the regression model given by equation [23], together with the coefficient of multiple determination. Figures [5] and ^[6] show the charts for Control Type I and Type II, respectively.

In Figure [4], one can see that there is a good adherence between the values read and the estimated values, even when the readings were taken at longer time intervals. Moreover, during the filling of the reservoir, between 1984 and 1986, and in 2008, when readings were taken at higher frequencies, one finds greater adherence to the regression curve.

Figure [5] shows that some points exceed the 1.96 and -1.96 limits, especially around May/24/2000. A similar situation was also found in Control Chart Type 2, shown in ^{Figure [6]}, where the curve of the regression values exceeds the lower limit. As stated earlier, this situation indicates a scenario with two possibilities: measurement error or change in dam behavior.

The construction of the second stage of the Tucuruí dam began in 1998 and was completed in mid-2006 [17]. These brought about several changes, such as demolition of cofferdams, as can be seen in Figure [7]. Certainly, such modifications caused these momentary changes in the behavior of the block under analysis which coincide with the period identified in both control charts.

5. Conclusion

Readings taken in overly-spaced time intervals results in "jumps" in time series, which reduce the precision of the prediction models. Even though, it was possible to achieve a good adjustment between the predicted and measured values and clearly detecting a process change, i.e., a change in structural behavior. In this research, the change in the structural behavior of the block was due to the construction of the second step of the plant, in which coffer dams had to be demolished. Possibly, other process changes such as those brought about by foundation settlement and instrument break-down could also be identified in this type of analysis.

The "jump" problem in the time series could be solved by having an online monitoring system, such as those employing of optical fiber technology. That type of system would have the capability to send an alarm to the technicians whenever the value read by the sensors overshot the limits set in the dam design phase and in the control charts.

The Control Chart Type I, for residual regression, has the advantage of more clearly showing the periods in which major differences occur between instrument readings and the predicted values. On the other hand, Control Chart Type II has the advantage of combining information on the dynamics of the process and the statistical control in a single chart.

6. Acknowledgements

The authors would like to thank ELETRONORTE, FINEP and FAPESPA for the financial supporting this research.

7. References

Received: 28 Apr 2011

Accepted: 05 Mar 2012

Available Online: 26 Jun 2012

• [01] HAMANN, F P. Engenharia invisivel. Rio de Janeiro, Desiderata, 2008.
• [02] ELETRONORTE. Auscultação da barragem de Tucuruí, após 20 anos de operação do reservatório. Relatório Técnico, Eletronorte, 2004.
• [03] CENTRO DA MEMÓRIA DA ELETRICIDADE NO BRASIL. ELETRONORTE 25 anos. Rio de Janeiro: Centro da Memória da Eletricidade no Brasil, 1998.
• [04] Quantific-Instrumentação Cientifica. Disponível em:www.quantific.pt/Quantific_CS_Odelouca.pdf Acesso em: 05 de maio de 2011.
• [05] PORTELA, E. T. A. Novas metodologias de apoio ao controlo de segurança de barragens de betão: uma abordagem através dos sistema periciais. Tese (doutorado), Lisboa, LNEC, 2001.
• [06] LEINº 12.334DE 20 DE SETEMBRO DE 2010.Casa civil, Subchefia para assuntos jurídicos.
• [07] OLIVEIRA, S. Modelos de dano na análise do comportamento de barragens de betão: roturas e efeitos do tempo. Exemplos de aplicação. Relatório técnico, Lisboa, LNEC, 2002.
• [08] DA MATA, J.T.C. Aplicação de redes neuronais ao controlo de segurança de barragens de betão. Dissertação (mestrado), Lisboa, Universidade técnica de Lisboa, 2007.
• [09] GOMES, M. F. et al. Controle do Deslocamento de Blocos de Concreto da UHE Tucuruí por Meio de Modelo Estatístico. , 50ş Congresso Brasileiro do Concreto, Salvador, 2008.
• [10] LOPES, R. A. C. et al. Emprego de modelo regressivo linear e rede neural artificial no controle da segurança de barragens de concreto. Revista Sul-Americana de Engenharia Estrutural, Passo Fundo, v.5, p.65-80, 2008.
• [11] CRUZ, P. T. 100 barragens brasileiras: casos históricos, materiais de construção, projeto. São Paulo, Oficina de Textos, 1996.
• [12] STEMATIU, D., SARGHIUTA, R., BUGNARIU, T., ABDULAMIT, A. Significance of Predicted Displacement Limits in arch dam safety. Barcelona, International symposium on new trends and guidelines on dam safety, 1988.
• [13] DEVORE, J. L. Probabilidade e estatística para engenharia e ciências. São Paulo, Thomson, 2006.
• [14] GUEDES, Q.M., De Faria, E.F. Modelo estatístico de controle do deslocamento monitorado na barragem casca da UHE Funil. Belém, XXVII Seminário nacional de grandes barragens, 2007.
• [15] MONTGOMERY, D. C., Runger, G. C. Estatística Aplicada e Probabilidade para Engenheiros. Rio de Janeiro, LTC, 2003.
• [16] PEDRINI, D. C. Proposta para um método de aplicação de gráficos de controle de regressão no monitoramento de processos. Dissertação (mestrado), Porto Alegre, UFRGS, 2009.
• [17] RSin07. Relatório Mensal de Análise do Sistema Interligado Nacional. ELETRONORTE, 2006.

Publication Dates

• Publication in this collection
  20 Sept 2012
• Date of issue
  June 2012