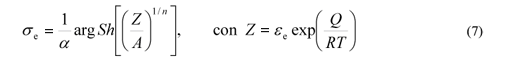Modelado numérico del proceso de soldadura por fricción agitación en aceros inoxidables

Numeric simulation of the friction-agitation welding process in stainless steels

Modelado numérico del proceso de soldadura por fricción agitación en aceros inoxidables

Numeric simulation of the friction-agitation welding process in stainless steels

Pereyra, S.^I; Lombera, G.^I; Urquiza, S.^I; Santiago, D.^I; De Vedia, L.A.^II

^IFac.de Ing.,Univ. Nac. de Mar del Plata, J. B. Justo 4302, Mar del Plata (CP 7600), Argentina-(CONICET). e-mails: [e-mail], [e-mail], [e-mail], [e-mail]

^IIUniversidad Nacional de San Martin, Av. Gral. Paz 1499 - San Martín (CP 1650), Buenos Aires, Argentina. e-mail: [e-mail]

RESUMEN

En el presente trabajo se modela el proceso de Soldadura por Fricción-Agitación (SFA) en aceros inoxidables mediante la utilización de un programa de elementos finitos de propósito general, reproduciendo el mapa térmico y la distribución del flujo del material.

En el proceso de SFA el equipo de soldadura consta de una herramienta que gira y se desplaza sobre la unión de dos chapas restringidas. La unión se produce por el calentamiento por fricción inducido por la herramienta, que promueve un comportamiento pastoso/viscoso del material y su correspondiente flujo entre las chapas a unir.

Este trabajo simula el proceso para una unión de aceros inoxidables austeníticos considerando acoplamiento termomecánico. Para la resolución del problema mecánico se utiliza un modelo viscoplástico con una ley constitutiva representativa de estos aceros en el rango de las temperaturas del proceso. Por otro lado, el problema térmico se modela teniendo en cuenta los fenómenos advectivos debidos al movimiento de la herramienta.

En esta primera etapa, los resultados obtenidos han sido contrastados con datos reportados en la bibliografía, obteniéndose una buena correlación entre los mismos.

Palabras clave: Métodos Numéricos, soldadura, análisis térmico

ABSTRACT

In this work the friction stir welding (FSW) process of stainless steel probes is modeled by a general propose finite element program, reproducing both thermal and material flow distribution.

In the FSW process the equipment consist essentially of a rotating tool, which travel along the joint of two restricted plates. The union results from the frictional heating induced by the tool, which led into a viscoplastic material flow between the joined plates.

This work simulates the process for a union of austenitic stainless steel considering thermo-mechanical coupling. In order to solve the mechanical problem, a viscoplastic model is implemented for this steel, involving a representative constitutive relation within the range of process temperatures. On the other hand, the related thermal problem is modeled considering the advection phenomena induced by the tool movement.

At this first stage, the results obtained have been contrasted with data reported in the published literature, obtaining good agreement between them.

Keywords: Numerical methods, welding, termal analysis.

1 INTRODUCCIÓN

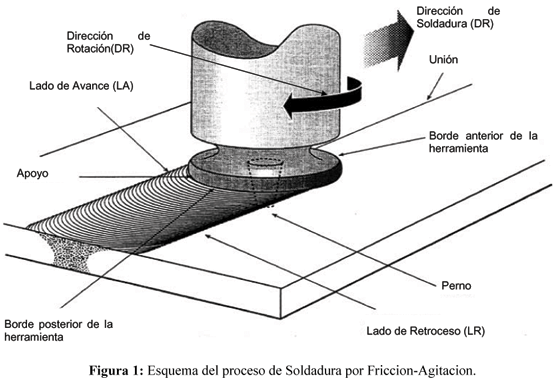
La Soldadura por Fricción-Agitación o "Friction stir welding" (FSW) es un proceso de unión en estado sólido relativamente nuevo y de gran aplicación tecnológica. La herramienta de soldadura está básicamente construida en una sola pieza y consta de dos partes, un perno y un apoyo (ver Fig. 1). El proceso consta de dos pasos. En el primero, manteniendo la herramienta rotando y sin velocidad de avance, se inserta el perno entre las piezas a unir hasta que el apoyo hace contacto con la superficie de dichas piezas. En el siguiente paso se le aplica una velocidad de avance a la herramienta en dirección de la línea de soldadura, generando la unión. La fricción generada entre la herramienta y las piezas a soldar producen el ablandamiento del material, el cual es forzado a fluir desde el frente de la herramienta hacia atrás a medida que la misma avanza.

Aunque es una tecnología de soldadura nueva, la SFA se ha estudiado ampliamente para la mayoría de las aleaciones de aluminio, inclusive las denominadas "difíciles de soldar" como las AA2195 (con litio) y AA7075. Existen diversos trabajos de simulación numérica de este proceso en uniones de aluminio. J.E. Gould y Z. Feng [1], desarrollaron un modelo analítico de flujo de calor para SFA. El modelo se basa en la bien conocida ecuación de Rosenthal [2], que describe un campo de temperaturas quasi-estacionario en una placa semi-infinita debido a una fuente de calor móvil. Kovacevic et al. [3],[4] realizó análisis térmicos y termomecánicos aplicando elementos finitos. Estos análisis se basan en un modelo de fuente de calor, sin contemplar el acoplamiento termomecánico provocado por el flujo plástico. Es de destacar que por las características del problema, donde las deformaciones plásticas son dominantes, pueden lograrse buenos resultados empleando modelos de flujo viscoplástico termomecánicamente acoplados (Ulysse [5]; Santiago et al.[6,7]; Colegrove et al.[8]).

En cuanto a la simulación de SFA en otro tipo de materiales, la bibliografía es escasa. Sin embargo, es de destacar el trabajo de Chao et al.[9] en modelado térmico de acero inoxidable 304L. En este trabajo el valor de la fuente de generación de calor por fricción se obtuvo haciendo análisis inverso. Para tener una mayor comprensión de los fenómenos involucrados en la SFA en aceros inoxidables y para mejorar la calidad de las uniones, es necesario desarrollar modelos numéricos de la distribución de temperaturas y flujo de material que complementen la información adquirida experimentalmente.

Con este propósito, en el presente trabajo se modeló la distribución de temperaturas y el flujo de material en un acero inoxidable 304L. Para tal fin, se utilizó un modelo de flujo viscoplastico para analizar la parte mecánica del problema y un modelo de convección- difusión en la parte térmica. El modelo se encuentra termomecanicamente acoplado por la generación de calor por disipación viscosa. Los datos de temperaturas obtenidos de la simulación, se compararon con valores experimentales reportados en bibliografía con el fin de validar el modelo.

2 ECUACIONES GOBERNANTES

2.1 Modelo mecánico

Despreciando las fuerzas inerciales y de volumen, las ecuaciones de equilibrio en un volumen de material Ω con una frontera ∂Ω se pueden escribir de la siguiente manera [10]:

donde σ es el tensor de tensiones de Cauchy. Las tracciones Tº_i se pueden describir en una porción de la frontera ∂Ω_t (condiciones de Neumann), mientras los componentes de la velocidad uº_i se puede especificar en el resto de la superficie ∂Ω_u (condiciones de Dirichlet). Esto se puede expresar como:

donde ∂Ω = ∂Ω_t ∪ ∂Ω_u y ∂Ω_t ∩ ∂Ω_u = Ø, n es la normal unitaria externa en el contorno ∂Ω, e_i es el vector unitario en un sistema de coordenadas cartesianas tridimensional y u el vector velocidad. El vector de velocidad de deformación está relacionado con la parte simétrica del gradiente del campo de velocidades de acuerdo a:

Suponiendo que el material es incompresible, luego la ecuación de continuidad que sigue se debe cumplir en todo el dominio Ω

Si se adopta una formulación de flujo para modelar las grandes deformaciones plásticas involucradas en el proceso de SFA, el tensor desviador de tensiones S se puede relacionar al tensor de velocidades de deformación D –que es en realidad un desviador en virtud de la hipótesis de incompresibilidad- por la siguiente relación:

donde µ es la viscosidad efectiva del material y p la presión hidrostática. Además, σ_e es la tensión efectiva o el segundo invariante de la tensión y ε_e es la velocidad de deformación efectiva o el segundo invariante de la velocidad de deformación. Estos se pueden escribir como:

En este trabajo se asumió un material viscoplástico y rígido donde la tensión de flujo depende de la velocidad de deformación y de la temperatura. Esto se representa por la siguiente relación (Sellars et al.[11]):

donde α, Q, A y n son constantes del material, R es la constante de los gases y T la temperatura absoluta. Los valores de las constantes fueron obtenidos del trabajo de Balancín et al[12] y son α = 0.012 MPa^-1, Q = 401 kJ/mol, A = 8.30 10¹⁵ y n = 4.32. El modelo mecánico se completa luego de describir las condiciones de contorno apropiadas.

2.2. Modelo Térmico

La distribución de temperaturas se obtiene resolviendo la ecuación de balance de calor [10]

donde ρ es la densidad, Cp la capacidad calorífica, k la conductividad térmica, θ la temperatura y γ la tasa de generación de calor interna por disipación de la potencia viscoplástica. Se asume que alrededor del 50% de la potencia plástica se convierte en calor [9]. El término de tasa de generación de calor por trabajado mecánico se puede expresar como el producto contraído de la tensión con la velocidad de deformación, como sigue:

siendo η la fracción de potencia que no es absorbida en defectos microestructurales.

Los flujos qº se pueden prescribir en una porción del contorno ∂Ω_q, mientras que la temperatura θº se puede especificar en el resto de la superficie ∂Ω_θ. Esto se puede expresar como:

donde ∂Ω = ∂Ω_q + ∂Ω_θ y n es la normal unitaria externa en el contorno ∂Ω , β es el coeficiente de perdida de calor por convección, ε es la emisividad de las superficien y B = 5.67 10⁻¹² (W cm^-2 ºC^-1) es la constante de Stefan–Boltzman. Las propiedades térmicas utilizadas en esta simulación se encuentran en la Tabla 1. La contribución de qº se debe al enfriamiento de la superficie por convección, por radiacion y a la transmisión de calor por contacto en las interfaces "placas-herramienta" y "placas-base".

3 MODELO GEOMÉTRICO

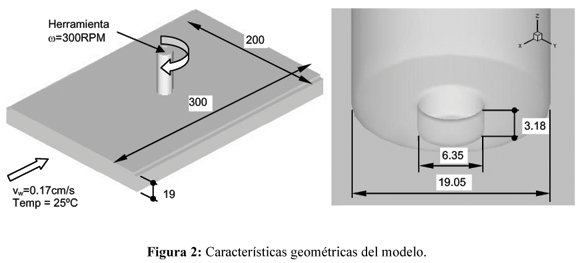
En el presente estudio se asume un marco de referencia fijado a la herramienta de soldadura, de tal manera que la placa se mueve hacia ella con una velocidad v_w=0.17cm/s y una temperatura de 25ºC impuestas en la superficie de entrada a la zona de estudio. La velocidad de rotación de la herramienta es ω=300RPM y se asume un deslizamiento relativo del 50% entre las superficies de la herramienta y las piezas a soldar.

La herramienta tiene un apoyo de 19.05mm de diámetro, y un perno de 6.35mm de diámetro una altura de 3.0mm. La pieza de trabajo tiene 300mm en la dirección de soldadura. 200mm en sentido transversal a ésta y un espesor de 3.18mm. La placa base se encuentra debajo de la pieza de trabajo y tiene un espesor de 19mm( ver Fig. 2).

4 MODELO NUMÉRICO

Se modeló la placa base con una malla de elementos finitos tetraédricos del tipo Taylor-Hood [10], es decir, tetraedros P2-P1, con interpolaciones cuadráticas para las velocidades y lineales para las presiones, en orden a lograr estabilidad de las interpolaciones de presión por la condición de divergencia nula conjuntamente con una adecuada captura de los gradientes de tensión en las capas límites. La malla implementada resultó tener aproximadamente 52800 elementos con 71000 nodos de velocidad.

El algoritmo de resolución consiste en dos subpasos: en el primero de ellos se obtiene el campo de velocidades asumiendo fijo el campo de temperaturas. Se itera por reemplazos sucesivos para adaptar no-linealmente los valores de viscosidad de acuerdo a las velocidades de deformación obtenidas en la iteración anterior. Las ecuaciones discretas son obtenidas a partir de la formulación clásica del problema de Stokes para flujos totalmente viscosos incompresibles y de acuerdo a las interpolaciones antes mencionadas, con el agregado de seudo-compresibilidad artificial del tipo de Chorin [13]. El sistema de ecuaciones lineales para cada iteración es resuelto por el método de gradientes conjugados cuadrados con un precondicionador de factorización incompleta de tipo LU de acuerdo al esquema propuesto por Y. Saad en SparseKit[14]. En el segundo sub-paso se resuelve el campo de temperaturas con interpolación cuadrática como un problema de convección difusión, asumiendo el campo de velocidades resultante en el primer sub-paso. El método de resolución numérica es el mismo que en el primero.

Aunque se requiere la solución estacionaria, se implementó un esquema de avance en el tiempo totalmente implícito, usado fundamentalmente como precondicionador del sistema de ecuaciones.

5 RESULTADOS

5.1 Distribución de Temperaturas

En la Fig. 3 se observa la distribución de temperaturas en las piezas de soldadura, la base y la herramienta. Se nota claramente el efecto del arrastre convectivo en el campo de temperaturas debido al avance de la herramienta. Los valores máximos de temperatura registrados fueron del orden de 1150ºC en la zona de contacto entre el apoyo y las placas.

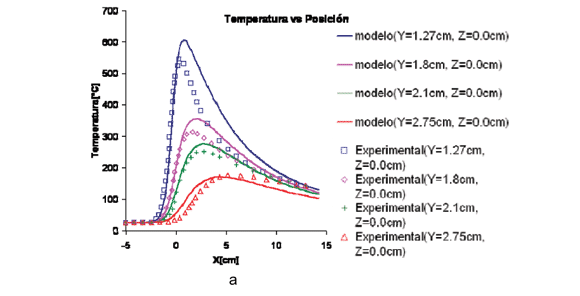
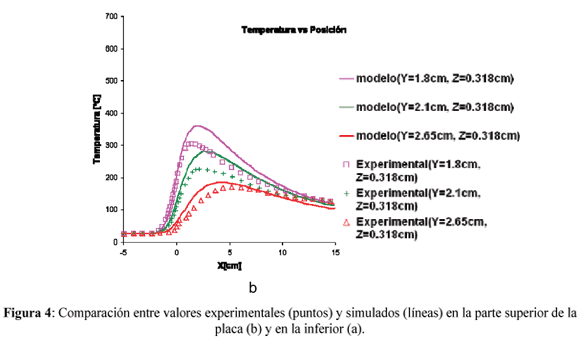
En la Fig. 4 se comparan los datos experimentales reportados en la bibliografía [9] con los obtenidos en la simulación para iguales condiciones del proceso de SFA. Los datos experimentales fueron obtenidos a partir de termocuplas fijas a las piezas de soldadura. A medida que la herramienta avanzaba, las termocuplas registraban el cambio de temperatura. Por tal motivo, las comparaciones con nuestro modelo fueron realizados para valores de "Y" y "Z" fijos en la geometría, variando la posición de "X" . En la Fig. 4.a se compararon los datos experimentales con los simulados en la parte inferior de las placas(Z=0) a 12.7mm, 18mm, 21mm y 27.5mm de la línea de unión, y en la Fig. 4.b para los posiciones de la parte superior de las placa(Z=3.18mm) a 18mm, 21mm y 26.5mm. Se observa que los valores de temperatura obtenidos en la simulación son superiores a los experimentales. En un principio, podríamos decir que las hipótesis de deslizamiento relativo entre las superficies del apoyo y las placas asumidas para resolver el modelo mecánico generan mayor flujo de material que el que existe realmente. En consecuencia, el modelo térmico trabaja con una generación de calor por disipación viscosa sobrevaluada, con el consecuente incremento de temperaturas.

5.2 Flujo de Material

En la Fig. 5 se muestran iso-superficies del modulo de la velocidad correspondientes a 3.4 mm/s (Fig 5a) , 17 mm/s (Fig 5b) y 34 mm/s (Fig 5c). En dicha figura se observa que el flujo de material para las velocidades mas próximas a las velocidades de soldadura (V_w=1.7mm/s) es mayor del lado de retroceso respecto al lado de avance (Fig 5a). En la Figura 5c la velocidad es veinte veces mayor a la velocidad de soldadura y la zona que delimita es prácticamente simétrica. Por lo tanto, podría considerarse que representa aproximadamente el límite entre la zona termomecánicamente afectada y la zona central sometida a plastificación y agitación. Esto se corresponde con los trabajos experimentales realizados por M. Guerra et al. [15] en aleaciones de aluminio, donde reporta una zona termomecánicamente afectada alrededor del perno que tiene al menos el doble de tamaño del lado de retroceso (LR) respecto al lado de avance (LA). Sin embargo, no se encuentran trabajos en bibliografía en los que se analice la microestructura en aceros inoxidables unidos por SFA.

6 CONCLUSIONES

Se presentó un modelo computacional tridimensional por Elementos Finitos del proceso de SFA aplicado al acero inoxidable austenítico 304. Los resultados obtenidos guardan una buena correlación con los reportados experimentalmente en la bibliografía.

Por otro lado, se reconoció la necesidad de aplicar condiciones de deslizamiento mas sofisticadas en la interface Herramienta-Placas con el fin de captar mejor los fenómenos de flujo de material alrededor del perno y, en consecuencia, mejorar los resultados del modelo térmico.

7 REFERENCIAS

Data de envio: 03/09/07 Data de aceite: 24/04/08

• [1] GOULD, J.E., FENG, Z., "Heat flow model for friction stir welding of aluminum alloys", Journal of Material Processing and Manufacturing Science, pp. 185-194, v. 7, 1998.
• [2] ROSENTHAL, D., SCHEMERBER, R., "Thermal study of arc welding", Welding Journal, v. 17, pp. 208, 1938.
• [3] CHEN, C.M., KOVACEVIC, R., "Finite element modeling of friction stir welding thermal and thermomechanical analysis", International Journal of Machine Tools and Manufacture, v. 43, pp. 1319-1326, 2003.
• [4] SONG, M., KOVACEVIC, R., "Thermal modeling of friction stir welding in a moving coordinate system and its validation", International Journal of Machine Tools and Manufacture, v. 43, pp. 605-615, 2003.
• [5] ULYSSE, P., "Three-dimensional modeling of the friction stir-welding process", International Journal of Machine Tools and Manufacture, v. 42, pp. 1549-1557, 2002.
• [6] SANTIAGO, D., LOMBERA, G., URQUIZA, S., CASSANELLI, A., DE VEDIA, L.A., "Numerical modeling of joints welded by "friction stir welding" process", Materials Research, v. 7, pp. 569-574, 2004.
• [7] SANTIAGO, D., LOMBERA, G., URQUIZA, S., CASSANELLI, A., DE VEDIA, L.A., "Analisis térmico en soldadura por fricción", Mecánica Computacional, v. 24, pp. 2781-2793, 2005.
• [8] COLEGROVE, P.A., SHERCLIFF, H.R., "3-Dimensional CDF modelling of flow round a threated friction stir welding tool profile", Journal of Material Processing Technology, v. 169, n. 2, pp. 320-327, 2005
• [9] ZHU, X.K., CHAO, Y.J., "Numerical simulation of transient temperature and residual stresses in friction stir welding of 304L stainless steel", Journal of Materials Processing Technology, v. 146, pp. 263272, 2004.
• [10] ZIENKIEWICZ, O.C., TAYLOR, R.L., The finite element method, v. I-II, London, McGraw Hill,1989, 1991.
• [11] SELLARS, C.M., TEGART, W.J., G, Mc., "La relation entre la résistance et la structure dans la deformation à chaud", Memories Scientifiques de la Revue de la Métallurgie, v. 63, pp. 731-746, 1966.
• [12] JORGE JR., A.M., BALANCINA, O., "Prediction of Steel Flow Stresses under Hot Working Conditions", Materials Research, v. 8, pp. 309-315, 2005.
• [13] CHORIN, A.J., "Numerical solution of the Navier-Stokes equations", Mathematics of Computation, v. 22, pp.745-762, 1968.
• [14] SAAD, Y., SPARSEKIT: a basic tool kit for sparse matrix computation (version2), University of Illinois, http://www-users.cs.umn.edu/ ~saad/software/SPARSKIT/sparskit.html, Accessed in1994.
• [15] GUERRA, M., SCHIMIDT, C., McCLURE, J.C., MURR, L.E., NUNES, A.C., "Flow patterns during friction stir welding", Materials Characterization, v. 49, pp. 95-101, 2003.

Fechas de Publicación

• Publicación en esta colección
  21 Ago 2008
• Fecha del número
  Jun 2008

Histórico

• Acepto
  24 Abr 2008
• Recibido
  03 Set 2007