Inhibited Quantum Processes Through Repeated Measurements: an Approach to Quantum Zeno Effect

Inhibited Quantum Processes Through Repeated Measurements: an Approach to Quantum Zeno Effect

Hilda A. Cerdeira

International Centre for Theoretical Physics,

P. O. Box 586, 34100 Trieste, Italy

G. Crespo and A. N. Proto

Laboratorio de Sistemas Dinamicos,

Centro Universitario Regional Martinez, UBA,

C.C. 15 SUC1 (1640) Martinez Argentina

Received May 9, 1997

The dynamics of a finite set of relevant observables, associated to a Hamiltonian of a three level system is analized in connection with the quantum Zeno effect. Since we use the Hamiltonian that completely describes the physical situation related to the experiment under study (W.M. Itano et al, Phys. Rev. A41, 2295 (1990)), no reduction or collapse of the wave function is required to describe the quantum Zeno effect.

I. Introduction

Some years ago, Misra and Sudarshan [1] introduced a problem into quantum mechanics theory which was called Zeno's paradox in quantum theory or simply quantum Zeno effect. They claimed, based on the usual quantum theory of measurement involving projection operators, that an unstable particle which was continuously observed to see whether it decayed would never be found to decay. Later, several authors [2-8] studied the problem and generalized the quantum Zeno effect to the inhibition of transitions or quantum jumps as the frequency of observation or measurements increased. The main feature of this effect lies on the fact that, apparently, the consequences of repeated measurements on a quantum system are not included in the Schrödinger equation.

Recently, renewed attention has been paid to this problem since Itano, Heinzen, Bollinger and Wineland [9] have informed they succeeded in observing this effect experimentally. Their experiment is, in fact, based on an experiment previously proposed by Cook (see Ref.(8)).

The experiment performed by Itano et al. involves transitions between three levels of ⁹Be⁺ ions. The transitions to be inhibited are transitions between the ground state (level 1) and an excited metastable state (level 2). The energy of the excited level 2 is higher than that of level 1 by w₂ which corresponds to radio frequency. By sending an on-resonance rf field, they create a coherent superposition state of levels 1 and 2 oscillating at the Rabi frequency W. If this rf field is applied during a time T = p/W adjusted to make it an on-resonance p pulse, this implies that after the time T all the ions initially in the ground level 1 will be brought into level 2. The state of this two-level system can be measured by use of a third level with very short lifetime (level 3, with energy higher than that of the ground level by w₃ > w₂) which is connected by a strongly allowed optical transition to level 1 and can decay only to level 1. The state measurement is made by applying a short on-resonance optical pulse (measurement pulse) to transitions 1« 3. If the ion is in state 1 at the start of this pulse, then it is quickly promoted to level 3, and, since this excited level 3 has a very short lifetime, the ion returns to level 1 after the end of the measurement through spontaneous emission of a photon. This photon in turn can be observed by fluorescence. On the other hand, if the ion is shelved in level 2 during this pulse, it is not available to undergo the fluorescence cycle 1« 3, and no fluorescence occurs. Thus, a strong optical pulse applied to transition 1« 3 measures the state of the two-level system: fluorescence indicates the system was found in level 1, and no fluorescence indicates the system was found in level 2. Moreover, the state of the system after the measurement is in accordance with the result of the measurement. Namely, if no fluorescence is observed, the system is left in level 2 after the measurement, and, when fluorescence is observed, either the electron is left in level 1 or it returns to this level very quickly. Therefore 1« 2 and 1« 3 transitions are allowed while 2« 3 transitions are forbidden.

Briefly summarizing the experiment by Itano et al.[9] we can say that the measurement sequence for the 1®2 transition was as follows: They initially prepared almost all the ⁹Be⁺ ions in level 1 and emptied level 2. Then, they applied a rf on-resonance p-pulse for T = 256 msec. This pulse would promote all ions from level 1 into the excited level 2. During the rf pulse, n optical pulses to transitions 1« 3, each of length t_p = 2.4 msec., were applied, where n was 1, 2, 4, 8, 16, 32, or 64. The delay from the beginning of the first optical pulse was (T/n - 1.3)msec. The time between the beginning of one optical pulse and the beginning of the next one was T/n. They assumed that each optical pulse produced a reduction of the wave function, and, by means of the projector operator techniques, derived the probability of finding the ion in level 2 at time T to be

They found that the agreement with the experimental results was quite good.

Shortly after, L.E. Ballantine [10] and T. Petrosky, S. Tasaki and I. Prigogine [11] presented notes in which they asserted that Itano et al's experimental results could be recovered through conventional quantum mechanics without resorting to a repeated reduction or collapse of the wave function. However, the article by Ballantine (indeed a comment by the article on Itano et al) in spite of describing the abovementioned experiment without resorting to any wave function collapse, did not mention any Hamiltonian that would describe the physical system either. On the other hand, the analysis by Petrosky et al. was made in terms of a split Hamiltonian: a Hamiltonian H governing the evolution of the system between measurement pulses, and a Hamiltonian H¢ governing the evolution during the measurement pulses. The wave function for the system at time T = (n + 1)T_p + nt_p, where T_p was the time between measurements, was found, through a recursive relation, to be

|y(T) > = [exp(-iHT_p)exp(-iH¢t_p)]ⁿ exp(-iHT_p) |y(0) > . (1.2)

In fact, in their analysis, Petrosky et al [11] used several approximations among which the most remarkable are the Wigner Weisskopf method [12] for treating spontaneous emission, and the assumption that photons emitted by successive pulses separated by a time larger than the lifetime of level 3 are incoherent. Finally, their main conclusion was that they could derive Eq.(1.1) of Itano et al. [9] through a quantum mechanical description without any appeal to repeated collapse of the wave function.

The disadvantage of the approach of Ref. [11] lies mainly on two facts: first, the authors did not actually take into account the dynamical presence of the level 3 in the system except for the justification to the using of the Wigner Weisskopf method, and second, the dynamical evolution of the system in terms of the wave function |y(t) > was obtained through a recursive relation (see Eq.(1.2)), due to the discontinuity imposed in the Hamiltonian which in fact led to the presence of two different Hamiltonians governing the evolution of the system.

The intention of the present effort is to introduce a different approach to this problem. Although we agree on the main conclusion of Refs. [10] and [11] concerning the fact that no reduction of the wave function is required in order to completely describe the quantum dynamics of the experiment by Itano et al.[9], we consider that the pertinent quantum system can be described completely by a single Hamiltonian, and that a better description continuous in time can be given in terms of the evolution of the expectation values of the relevant operators associated to this Hamiltonian. At this point , it is worth mentioning the fact that the dynamics thus obtained fully describes the so called process of decoherence (see Ref.[13] and references therein). This process refers to a system that loses quantum coherence (in this case the coherence between levels 1 and 2) due to the quantal interaction with an enviroment (in this case the electromagnetic field through its coupling with level 3).

This paper is organized as follows: in Sec. II we present an alternative description of the problem in terms of a two level Hamiltonian and the relevant operators related to it, in order to introduce our approach to the problem; in Sec. III we start from a three level approach to reach the complete Hamiltonian of the system, and obtain, after some approximations, the set of evolution equations for the expectation values of the relevant operators, which are numerically integrated to yield the same results as in Eq.(1.1) but through an embodying quantum dynamical procedure. Finally, in Sec. IV, some conclusions concerning the so-called quantum Zeno effect are drawn.

II. Two level system description of the problem

The analysis made by Itano et al [9] and Cook [8] in order to obtain the expression for the probability of finding an ion into level 1 or level 2, does not take into account the presence of the level 3. This probability is derived by considering the time evolution of the density matrix r describing a two level system. These authors claim that the consequence of the measurement pulse is to project an ion into level 1 or level 2, thus destroying the superposition existing between these two states (reduction of the wave function). This fact in turn corresponds to setting the coherences (r₁₂ and r₂₁) of the density matrix to zero.

When one is dealing with a dynamical description of a two level system achieved by the temporal evolution of the expectation values of the relevant operators imposed by the dynamics, it is pertinent to find the dynamical behaviour that proves to be tantamount to that of setting the coherences of the density matrix to zero.

A Hamiltonian describing the simplest interaction of a two level system can be written as

^
H = g₁₂ ^
a 1 ^
a +
2 +g^*₁₂ ^
a 2 ^
a +
1 (2.1)

where = 1.

It is easy to prove that, using the generalized Ehrenfest theorem, [14] by defining the following set of relevant operators

^
N 1 = ^
a +
1 ^
a 1 (2.2a)

^
N 2 = ^
a +
2 ^
a 2 (2.2b)

^
N 12 = i(g₁₂ ^
a 1 ^
a +
2 -g^*₁₂ ^
a 2 ^
a +
1 (2.2c)

the temporal evolution of the expectation values of these operators is governed by:

Because of the very definition of these relevant operators,

₁ and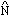 ₂ are the number of particles or populations of level 1 and 2, respectively, and 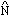₁₂ is related to the current of particles between these two levels.

The set of equations (2.3) can be easily solved, and if one sets the interaction constant g₁₂ appropriately, one obtains, as expected, the Rabi oscillations between levels 1 and 2.

In order to compare this approach to that used by Itano et al [9] and Cook [8], it is convenient to normalize the expectation value of the total number of particles of the system to one, i.e. <

₁ > + <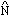 ₂ > = 1, so that < 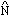₁ > and < 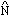₂ > thus represent the probabilities of finding the particle in level 1 or in level 2, respectively.

The dynamical equivalent of setting the coherences in the density matrix to zero in order to provide the so-called collapse of the wave function due to the measurement performed on the system, is found to be the setting of the expectation value of the current of particles, i.e. <

₁₂ > , to zero. In the case of the experiment made by Itano et al [9] this can be achieved modifying Eq.(2.3c) by letting <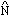 ₁₂ > rapidly decay during the pulse of measurement. In an attempt to artificially reproduce the dynamical behaviour expected, we can modulate a strong exponential decay by narrow gaussian functions. These gaussian functions would be present only at the measurement pulses, and their width (proportional to s) related to the length of the measurement pulse. Thus, the Eq.(2.3c) would turn into

where N is the number of measurements made during the period T. In order to reproduce the experimental results, we set T = 0.26 sec, s = 0.001 sec, and D = 0.0013 sec, on the one hand, and letting g₁₂ = 6.14 sec^-1, so as to adjust the p pulse (from analytical integration of Eqs.(2.3a-c). It is straightforward to see that the oscillating Rabi frequency W of the system equals W = 2|g₁₂| and therefore, as a p pulse is characterized by WT = p, one is led to the previous value of g₁₂). The time evolution of the number of particles of levels 1 and 2 for the particular case of N = 4, which were obtained through numerical integration of Eqs. (2.3), is shown in Fig. 1. We can see that the numerical results are in complete agreement with the expected values (either experimental or theoretical, according to Refs.[8] and [9]). In Fig. 2 we depict the temporal evolution of < 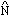₁₂ > , showing that the expectation value of the current of particles between levels 1 and 2 goes to zero in each pulse.

Figure 1.
Temporal evolution of <

Figure 2.
Temporal evolution of <

III. Three level system description

When considering carefully the details of the experiment proposed by Itano et al [8], it is necessary, in order to try to obtain a complete dynamical description of the quantum process involved, to include the third atomic level.

Therefore, a three level system, in which there exists a constant interaction between the first and second levels (namely the one provided by the p pulse), and a strongly driven interaction between levels 1 and 3 existing only at very short periods (namely the measurement pulses), can be written as

^
H 0 = g₁₂ ^
a 1 ^
a 2 +g^*₁₂a₂ a₁⁺+f(t)(g₁₃ ^
a 1 ^
a 3 +g^*₁₃a₃ a₁⁺ (3.1a)

where we can define f(t) as a succession of very narrow gaussian functions centred around the measurement times. Thus,

with N, T, D, and s defined as in Sec. II. At this stage, it is pertinent to notice that we are particularly interested in the dynamical evolution of the expectation values of the operators:

^
O 1 = ^
a +
1 ^
a 1 (3.2a)

^
O 2 = ^
a +
2 ^
a 2 (3.2b)

^
O 3 = ^
a +
3 ^
a 3 (3.2c)

since they represent the particle number operators of levels 1, 2 and 3, respectively. As was mentioned before, the normalizing condition <

₁ > + < ₂ > + < ₃ > = 1 turns these expectations values into the probabilities of finding the atom in level 1, 2 and 3, respectively. In order to obtain the dynamical equations for the expectation values of the operators (3.2a-c), this set must be augmented to include the following relevant operators:

^
O 4 = i(g₁₂ ^
a 1 ^
a +
2 -g₁₂ ^
a 2 ^
a +
1 ) (3.2d)

^
O 5 = i(g₁₃ ^
a 1 ^
a +
3 -g₁₃ ^
a 3 ^
a +
1 ) (3.2e)

^
O 6 = g₁₃g₁₂^* ^
a 2 ^
a +
3 +g^*₁₃g₁₂ ^
a 3 ^
a +
2 ) (3.2f)

so as to close a semialgebra under commutation with the Hamiltonian (3.1a), yielding

[ ^
H 0 , ^
O 1 ] = -i ^
O 4 -if (t) ^
O 5 (3.3a)

[ ^
H 0 , ^
O 2 ] = i ^
O 4 (3.3b)

[ ^
H 0 , ^
O 3 ] = if (t) ^
O 5 (3.3c)

[ ^
H 0 , ^
O 4 ] = i2|g₁₂|²( ^
O 1 - ^
O 2 )-if (t) ^
O 6 (3.3d)

[ ^
H 0 , ^
O 5 ] = if(t)2|g₁₃|²( ^
O 1 - ^
O 3 )-i ^
O 6 (3.3e)

[ ^
H 0 , ^
O 6 ] = i|g₁₂|² ^
O 5 +if(t)|g₁₃|² ^
O 4 (3.3f)

which in turn defines the following system of differential equations for the expectation values of these operators:

Due to the presence of the function f(t), this system has time dependent coefficients, which does not allow for a direct analytical integration.

The new operators appearing in Eqs.(3.3a-f) in order to close the semialgebra under commutation with

₀, deserve the following comment: < ₄ > and < ₅ > are operators defining the current of particles between levels 1 and 2 and between levels 1 and 3, respectively. The interactions between these levels were the ones included in the Hamiltonian (3.1a). On the other hand, < ₆ > represents a kind of "bridge" interaction between levels 2 and 3 (notice the products g₁₃g^*₁₂ and g^*₁₃g^*₁₂) that is imposed by the dynamics of the problem, in spite of the fact that a direct interaction between these two levels is not included in the Hamiltonian < ₀ > .

Nevertheless, the Hamiltonian given by Eq.(3.1a) does not yet take into account all the physical characteristics involved in the experiment of Ref. (9), since it does not include the spontaneous emission that occurs when an atom decays from level 3 to level 1, owing to the very short lifetime in the upper level. Thus, the Hamiltonian should be modified according to

^
H = ^
H 0 + ^
H 1 (3.5a)

with

^
H 1 = ¥
å
k = 1 {(w_k-w₃) ^
b k + ^
b k +(g_k ^
a 1 ^
a +
3 a_k+g^*_k ^
a 3 ^
a +
1 ^
b +
k (3.5b)

where the rotation wave approximation is used.

The Hamiltonian

₁ will be considered a perturbation to the Hamiltonian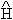 ₀. The first of the two summations in 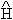₀ accounts for the quantized electromagnetic field, while the second one describes the interaction that allows for the destruction of a particle in level 3, its creation in level 1 and the creation of a photon in the electromagnetic field (plus H.C.).

The difficulty that arises when dealing with the Hamiltonian given by Eqs. (3.5) is that it is no longer possible to close a finite semialgebra of operators under commutation with the Hamiltonian starting from the set given by (3.2a-c). This is due to the presence of trilinear operator terms appearing in the last summation of Eq.(3.5b), whose effect is to introduce new operators of higher order than trilinear. Therefore we can ascertain that it is not possible to obtain an exact analytical resolution of the dynamical equations for the expectation values of the relevant operators related to the Hamiltonian (3.5a).

Nevertheless, if the Hamiltonian

₁ is taken as a perturbation on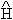 ₀, we can make some approximations in order to transform the problem into a manageable one.

To start with, it is easy to see that

[ ^
H , ^
O 1 ] = -i ^
O 4 -if(t) ^
O 5 + ¥
å
k = 1 ( ^
A k - ^
A +
k ) (3.6a)

[ ^
H , ^
O 2 ] = i ^
O 4 (3.6b)

[ ^
H , ^
O 3 ] = if(t) ^
O 5 + ¥
å
k = 1 ( ^
A +
k - ^
A k ) (3.6c)

where we define, following Ref.(15), the non-hermitian

_k operator according to

^
A k = g_k ^
a 1 ^
a +
3 ^
b k . (3.7)

We are now interested in obtaining the temporal evolution of the expectation value of

_k. In order to do so, we compute

[ ^
A , ^
A k ] = -(w_k-w₃) ^
A k -|g_k|² ^
A 3 -g^*₁₂g_k ^
a 2 ^
a +
3 ^
b k

At this level, we neglect the third and fourth term in Eq.(3.8) due to the fact that they introduce interactions between levels and the electromagnetic field that are not present in the Hamiltonian of the system, and also neglect the last term for the same reason in addition to the so-called Born approximation [15-17] (which neglects corrections that would introduce terms of equal or higher order than O(g²_k)). Therefore, after these approximations, we obtain

which can be formally integrated to yield

and, by direct hermitean conjugation,

From Eq.(3.6a), we obtain

Replacing Eqs.(3.10a,b) into Eq.(3.11a) yields

If we now use the Markov approximation [15-17] (assuming that the decay time of the atomic system is much longer than w^-1₃), we can replace by < ₃ > (t¢) by < ₃ > (t) inside the integral and let the upper limit go to infinity. Then, if we perform the change of variables t = t - t¢ and define I_k = ò^¥₀cos(w_k-w₃)tdt, we finally obtain

where

a = |
å infty_{k = 1}2|g_k|²I_k . (3.12b)

Now, it is straightforward to verify that, following the same procedure as above, one obtains:

Therefore, we have shown so far that the perturbative treatment of

₁ allows for the dynamical description of the spontaneous decay between levels 3 and 1. We will now examine further the consequences of this perturbation on the rest of the evolution equations for the expectation values of the relevant operators, namely Eqs.(34d-f).

First, we have to compute the following commutators:

[ ^
A , ^
O 4 ] = i2|g₁₂|²( ^
O 1 - ^
O 2 )-if(t) ^
O 6 (3.14a)

where the following non hermitian operators have come up

^
B k = g_kg^*₁₃ ^
b k a⁺₁ ^
a 1 (3.15a)

^
C k = g_kg^*₁₃ ^
b k ^
a +
3 ^
a 3 (3.15b)

^
D k = g_kg^*₁₃g₁₂ ^
b k ^
a +
2 ^
a 1 (3.15c)

Therefore, it is now necessary to calculate the temporal evolution of the expectation values of the operators given by Eqs.(3.15a-c).

Thus, we compute

At this point, we will neglect the last five terms in Eq.(3.16a) under the following approximations: a) all of these terms represent interactions between the atom levels and the electromagnetic field not belonging to the model adopted for the system we want to describe, and b) the last three terms contribute with corrections introducing terms of equal or higher order than O(g²_k) (the Born approximation, see Refs. (15), (16) and (17)), on the other. It should also be noticed that, in spite of the fact that the third term equals 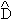_k, it is all the same neglected at this level since it is a correction to the evolution of 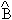_k and not to the evolution of the relevant operators (see Eq.(3.14c)).

Therefore we can write

[ ^
H , ^
B k ] = -(w_k-w₃) ^
B k -i ^
e k (t) ^
O 5 (3.16b)

where we have defined the following non hermitian time-dependent operator

^
e k (f) = f(t)g_kg^*₁₃ ^
b k . (3.17)

Thus, if one makes the approximations that have just been described, it can also be easily proven that

[ ^
H , ^
C k ] = -(w_k-w₃) ^
C k +-i ^
e k (t) ^
O 5 (3.18)

Therefore, in order to complete the equation of motion for <

₅ > , we have to calculate the temporal evolution of <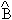 _k- 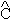_k > (t) (see Eq.(3.14b)). From Eqs.(3.16b) and (3.18), we can write

where we have explicitly uncorrelated operators

_k(t) and ₅. Then, we obtain

< ^
B k - ^
C k > (t) = 2 ó
õ t

0 < ^
e k (t¢) > < ^
O 5 > (t¢)dt¢ (3.20a)

Finally, using the Markov approximation [15-17] into the integral in Eq.(3.20a), this equation turns into

< ^
B k - ^
C k > (t) = < ^
O 5 > (t) ó
õ ¥

0 < ^
e k (t¢) > dt¢ (3.20b)

and also, by taking the hermitian conjugate, we can write

< ^
B +
k - ^
C +
k > (t) = 2 < ^
O 5 > (t) ó
õ ¥

0 < ^
e +
k (t¢) > dt¢ (3.20c)

Thus, replacing Eqs.(3.20b,c) into Eq.(3.14b), we finally arrive at the equation of motion

where

b = ¥
å
k = 1 2 ó
õ ¥

0 ( < ^
e k (t¢) > + < ^
e +
k (t¢) > )dt¢ (3.22)

can be regarded as a parameter which depends, among other things, on the number of measurement pulses N through f(t) (see Eq.(3.1b)).

Therefore, the last thing that is left to study in order to complete the present analysis is the temporal evolution of the expectation value of

_k so as to evaluate the perturbation introduced to the equation of motion for < ₆ > (see Eqs.(3.14c) and (3.15c)). Thus, we compute

We now make a drastic approximation as we will neglect the last three terms in Eq.(3.23a), on the basis of the following criteria: first,

₆ is an operator imposed by the dynamics of the problem to first order (see Eqs.(3.3d-f)) but describing an interaction which is not present by itself in the Hamiltonian of the system; second, the appearance of operators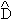 _k (or 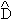⁺_k) is a consequence of the perturbative Hamiltonian on the dynamics of ₆ (see Eq.(3.14c)). So, we neglect these last three terms in a truncation of the successive approximations just described.

Therefore, we can write

[ ^
H , ^
D k ] = -( ^
e k (t)+ ^
e +
k (t)) ^
O 6 (3.23b)

obtaining

where we have also explicitly uncorrelated operators

_k(t),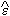 ⁺_k(t) and ₆. By using the Markov approximation [15-17] on integrating Eq.(3.24), we see that

< ^
D k > (t) = -i < ^
O 6 > (t) ó
õ ¥

0 < ^
e k (t¢)+ ^
e +
k (t¢) > dt¢ (3.25a)

and, consequently,

< ^
D +
k > (t) = i < ^
O 6 > (t) ó
õ ¥

0 < ^
e k (t¢)+ ^
e +
k (t¢) > dt¢ (3.25b)

Finally, using Eqs.(3.25a-b) and (3.14c), we arrive at the equation of motion for <

₆ > :

where b is given by Eq.(3.22).

Summarizing, we have obtained, under the above mentioned approximations, that the Hamiltonian 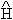(Eq.(3.5a)) leads, for the expectation values of the relevant operators described by Eqs.(3.2a-f), to the following set of differential equations

where a and b are defined according to Eqs.(3.12b) and (3.22). It is important to notice that, recourse to these equations, a depends on the electromagnetic field and its coupling constants to the atom, and b depends not only on the electromagnetic field and its coupling to the atom but also on the function f(t) which modulates the measurement pulses.

On inspecting the system (3.27) we can immediately see that it is a system of linear differential equations but with time dependent coefficients. Due to the complexity of these time dependent coefficients, the integration of (3.27) can only be achieved numerically. In order to see the features of this model, in Figs. (3-17) we depict the dynamical evolution of the operators < ₁ > , < ₂ > , < ₃ > and < ₄ > obtained by numerical integration of the system (3.27) through the Runge-Kutta method, for N = 1, 2, 4, 8, 16, 32 and 64, respectively (N, as defined before, is the number of measurement pulses). The number of measurement pulses was chosen so as to compare our results with the experiment proposed in Ref.(9). In order to reproduce the strong spontaneous decay from level 3 to level 1, we set a = 2000 sec^-1, except for the Figs. (15) and (16) where we set a = 8000 sec^-1 due to the high frequency to the measurement pulses. So as to clarify this point, we reproduce in Figs. (17) and ⁽¹⁸⁾ the same physical situation as in Figs. (7) and (8) but with the value a = 20000 sec^-1 obtaining the same final results for < ₁ > and < ₂ > . Depending on the number of measurement pulses, the value of b was adjusted in order to provide the expected dynamical behaviour of < ₄ > . In spite of the fact that in all cases the agreement with the expected results was quite good, we have to notice that the first measurement pulse does not yield for < ₄ > such a good approach to zero as in the following pulses. Finally, we have chosen g₁₃ = (800000)^1/2 sec^-1, related to the strong optical transition 1®3.

Figure 3. Temporal evolution of <

₁ > , (a) < ₂ > and < ₁ > (c) (namely, the expectation values of the number of particles of level 1, 2 and 3) for the particular values of a = 2000 sec^-1, b=20 sec^-1 and number of measurement pulses N = 1 (see Eqs.(3.27a-3.27f). Final values of < ₁ > =0.00122 and < ₂ > =0.99878.

Figure 4. Temporal evolution of <

₄ > (namely, the expectation value of the current of particles between level 1 and 2) for the particular values a=2000 sec^-1, b=20 sec^-1 and number of measurement pulses N=1.

Figure 5. Temporal evolution of the operators <

₁ > (a), < ₂ > (b) and < ₃ > (c) (namely, the expectation values of the number of particles of level 1, 2 and 3) for a = 2000 sec^-1 and b = 35 sec^-1, and number of measurement pulses N = 2 . Final values of < ₁ > =0.49903 and < ₂ > =0.50090.

Figure 6. Temporal evolution of <

₄ > (namely, the expectation value of the current of particles between level 1 and 2) for a = 2000 sec^-1 and b = 35 sec^-1 and the number of measurement pulses N = 2.

Figure 7. Temporal evolution of <

₁ > (a) , < ₂ > (b) and < ₃ > (c) (namely, the expectation values of the number of particles of level 1, 2 and 3) for the particular values for a = 2000 sec^-1, b = 67.5 sec^-1 and number of measurement pulses N = 4. Final values of < ₁ > =0.62791 and < ₂ > =0.37200.

Figure 8.
Temporal evolution of <

Figure 9. Temporal evolution of <

₁ > (a), < ₂ > (b) and < ₃ > (c) (namely, the expectation values of the number of particles of level 1, 2 and 3) for the particular values for a =2000 sec^-1, b = 100 sec^-1, and number of measurement pulses N = 8. Final values of < ₁ > =0.77979 and < ₂ > =0.22010.

Figure 10. Temporal evolution of <

₄ > (namely, the expectation value of the current of particles between level 1 and 2) for the particular values a = 2000 sec^-1 and b=100 sec^-1, N = 8.

Figure 11. Temporal evolution of <

₁ > (a), < ₂ > (b) and < ₃ > (c) (namely, the expectation values of the number of particles of level 1, 2 and 3) for the particular values for a =2000 sec^-1, b =160 sec^-1, N = 16. Final values of < ₁ > =0.88720 and < ₁ > =0.11268.

Figure 12. Temporal evolution of <

₄ > (namely, the expectation value of the current of particles between level 1 and 2) for the particular values a = 2000 sec^-1 and b = 160 sec^-1, N = 16.

Figure 13. Temporal evolution of <

₁ > (a), < ₂ > (b) and < ₃ > (c) (namely, the expectation values of the number of particles of level 1, 2 and 3) for the particular values a =2000 sec^-1, b =255 sec^-1, N = 32. Final values of < ₁ > =0.95173 and < ₂ > =0.04815.

Figure 14. Temporal evolution of <

₄ > (namely, the expectation value of the current of particles between level 1 and 2) for the particular values a = 2000 sec^-1 and b =255 sec^-1, N = 32.

Figure 15. Temporal evolution of <

₁ > (a), < ₂ > (b) and < ₃ > (c) (namely, the expectation values of the number of particles of level 1, 2 and 3) for the particular values for a =8000 sec^-1, b =442 sec^-1, N = 64. Final values of < ₁ > =0.98508 and < ₂ > =0.01494.

Figure 16. Temporal evolution of <

₄ > (namely, the expectation value of the current of particles between level 1 and 2) for the particular values a =8000 sec^-1 and b =442 sec^-1, N = 64.

Figure 17. Temporal evolution of <

₁ > (a), < ₂ > (b) and < ₃ > (c) (namely, the expectation values of the number of particles of level 1, 2 and 3) for the particular value of a = 20000 sec^-1 and same physical situation as in Fig. 7. Final values of < ₁ > =0.62348 and < ₂ > =0.37165.

Figure 18. Temporal evolution of <

₄ > (namely, the expectation value of the current of particles between level 1 and 2) for the particular value of a = 20000 sec^-1 and same physical situation as in Fig. 8.

IV. Conclusions

The advantage of the approach developed in this paper is by itself obvious: we have found a finite set of relevant observables, namely {

₁, ₂, ₃, ₄, ₅, ₆, } that completely describes the evolution of the quantum system described by the Hamiltonian (3.5) through the differential equations (3.27). The introduction of the last terms in Eqs.(3.27a,c,e,f) is a direct consequence of the presence of 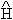₁ in the Hamiltonian of the system (see Eqs.(3.5) and Eqs.(3.4)). The validity of the approximations that were made in order to reach this final set of equations is justified by the success of these equations in reproducing the expected results. As mentioned before, the parameter a (see Eq.(3.12b)) depends basically on the strength of the coupling between the electromagnetic field and the atom and allows for the spontaneous decay from level 3 to level 1. On the other hand, the parameter b (see Eqs. (3.17) and (3.22)) also depends on the number of measurement pulses through the function f(t). It is interesting to notice that the presence of the last terms in Eqs.(3.27e,f), namely the ones with the factor b, allows for the required fact that the expectation value of the operator related to the current of particles between levels 1 and 2, i.e. < ₄ > , goes to zero after each measurement pulse. It is worth stressing the fact that this dynamical behaviour is not obtained by artificially manipulating the corresponding evolution equation (3.27d), as it has been done in Sec. II for the two level approach to the problem. Moreover, the presence or not of 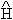₁ in the Hamiltonian does not modify the evolution equation for (c.f. Eq.(3.4d) and Eq. (3.27d)). This different dynamical behaviour is therefore strictly related to the appearance of the last two terms in the evolution equations for < ₅ > and < ₆ > (c.f. Eqs.(3.4e,f) and Eqs.(3.27e,f)).

Finally, we can conclude that the set of differential equations (3.27), concerning the temporal evolution of the expectation values of the relevant operators belonging to the dynamics of the Hamiltonian (3.5), fully reproduces the experimental results of the experiment by Itano et al. It should be noticed that we have not made use of any reduction or collapse of the wave function of the system, since the proper Hamiltonian completely describing the physical situation related to the experiment under study is used. Regarding this particular point, our work is in accordance with Refs.[18] and [19], although different methods were employed. Moreover. we could conclude that our quantum dynamical treatment is essentially indicating that the experiment of Itano et al [9] constitutes a concrete experimental example of the decoherence process fully described by V. Zurek (Ref.[13]). The environment (in this case the electromagnetic field) would be playing the role of the observer as it monitors the system, causing the decoherence between levels 1 and 2. The relevant aspect lies on the fact that this decoherence process comes out as a consequence of the complete quantum dynamical description of the system.

Acknowledgments

We are particularly grateful to Prof. N. Rahman and Prof. A. Colavita for enlightening discussions. G.C. also wishes to thank Dr. G. Pérez and Dr. C. Lambruschini Pando for valuable comments and references. We are also grateful for the computer facilities given by the International Centre for Theoretical Physics. A.N.P. acknowledges support from Comision de Investigaciones Cientificas de la Pcia de Buenos Aires. Finally, G.C. and A.N.P. fully acknowledge the hospitality of the International Centre for Theoretical Physics and H. A. C. acknowledges support from the Istituto Nazionale di Fisica Nucleare.

References

1.
• B. Misra and E.C.G. Sudarshan, J. Math. Phys. 18, 756 (1977).
2.
• C.B. Chiu and E.C.G. Sudarshan, Phys. Rev. D16, 520 (1977).
3.
• A. Peres, Am. J. Phys. 48(11), 931 (1980).
4.
• H. Dehmelt, Proc. Natl. Acad. Sci. U.S.A. 83, 2291 (1986); 83, 3074 (1986).
5.
• W. Nagourney, J. Sandberg and H. Dehmelt, Phys. Rev. Lett. 56, 2797 (1986).
6.
• M. Porrati and S. Putterman, Phys. Rev. A36, 929 (1987).
7.
• R.J. Cook and H.J. Kimble, Phys. Rev. Lett.54, 1023 (1985).
8.
• R.J. Cook, Phys. Scr. T21, 49 (1988).
9.
• W.M. Itano, D.J. Heinzen, J.J. Bollinger and D.J. Wineland, Phys. Rev. A41, 2295 (1990).
10.
• L.E. Ballantine, Phys. Rev. A43, 5165 (1991).
11.
• T. Petrosky, S. Tasaki and I. Prigogine, Phys. Lett. A151, 109 (1990).
12.
• G.S. Agarwal, Quantum Statistical Theories of Spontaneous Emission and their Relation to Other Approaches, Springer Tracts in Modern Physics, Vol. 70, p.9 (Springer-Verlag Berlin Heidelberg New York, 1974).
13.
• Wojciech H. Zurek, Phys. Today 44, 36 (1991).
14.
• A.N. Proto, in Proceedings of the X3 International Workshop on Condensed Matter Theories, edited by V. Aguilera-Navarro (Plenum, New York, 1989); J. Aliaga, G. Crespo, and A.N. Proto, Phys. Rev. A42, 618 (1990); J. Aliaga, G. Crespo, and A.N. Proto, Phys. Rev. A44, 2066 (1991).
15.
• C. Leonardi, F. Persico and G. Vietri, Rivista del Nuovo Cimento, Vol.9(4) (1986).
16.
• Ke Hsueh LI, Phys. Rep. 134(1) (1986).
17.
• F. Haake, Statistical Treatment of Open Systems by Generalized Master Equations, in: Springer Tracts in Modern Physics vol.66 (Springer, Berlin, Heidelberg, New York, 1973) p.98.
18.
• E.Block and P.R. Berman, Phys. Rev. A44, 1466 (1991).
19.
• V.Frerichs and A. Schenzle, Phys. Rev. A44, 1962 (1991).

Publication Dates

• Publication in this collection
  14 June 1999
• Date of issue
  Dec 1997

History

• Received
  09 May 1997