From the Atomic Systems to the Extended Ones: the Hubbard Operators

From the Atomic Systems to the Extended Ones:

the Hubbard Operators

M. E. Foglio

Instituto de Física `Gleb Wataghin',

Universidade Estadual de Campinas, Unicamp

13083-970 Campinas, São Paulo, Brazil

In commemoration of Roberto Luzzi's 60th birthday

Received April 15, 1997

It is sometimes convenient to emphasize the local aspects of a part of a crystalline system, and use the corresponding localized states to build a basis of the states of the whole system. In many cases it is only a subspace of these local states that is relevant, and the Hubbard operators provide a fairly simple way to write the corresponding projected Hamiltonian. Two examples of this type of treatment are presented int this work. The first is a Co²⁺ impurity in a MgO crystal interacting through a Jahn-Teller term with the crystal phonons, and it is shown how this interaction affects the electronic Raman scattering. The second is the Anderson lattice when the local electrons have an infinite Coulomb repulsion, and a diagrammatic expansion with cumulants is discussed. We propose a method to obtain approximate Green's functions for the Anderson lattice that employs the exact solutions of an atomic problem, and the corresponding spectral density of the local electrons is calculated

I. Introduction

In the study of solid state systems, it is sometimes interesting to focus on the local states of the ions placed at the different sites of the crystal, either because they can be considered as the building blocks of the system, like in the tight binding method, or else because one is interested in the properties of a particular ion immersed in the solid, like in the study of the paramagnetic resonance, or in the Raman scattering of impurities. An example of each of these two situations will be presented by considering the two following systems: a Co²⁺ impurity in a MgO crystal[1] and the Anderson lattice with an infinite repulsion between the local electrons[2] (this corresponds to U® ¥ for the model parameter U).

The space of the local or ionic states, associated to a given site, usually contains many states that are of little interest, generally because their occupation can be neglected at fairly low temperatures or frequencies when they are too far apart in energy from the ground state. It is then useful to eliminate these states from the model of the system, and the Hubbard operators[3, 4] are very convenient for that purpose. We shall consider in turn the two problems mentioned above, and show how the Hubbard operators are used in those two typical cases.

In the case of a Co²⁺ impurity in MgO we define the Hubbard operators associated to the impurity site, and use them to write the projection of the Hamiltonian of a Co²⁺ ion, that is within a cubic field, into a subspace of the lowest energy states. The electronic Raman scattering of a Co²⁺impurity in a MgO crystal, when the phonons interact with the Co²⁺ by means of a Jahn Teller term, is then expressed by employing time dependent averages of Hubbard operators[5, 6]. These averages are obtained by decoupling the equations of motion of double time Green's functions (GF)[7], and the resulting theoretical results of the Raman scattering are compared with the experimental values[5].

For the Anderson lattice it is necessary to define Hubbard operators at all the sites of the crystal. The corresponding Hamiltonian describes a whole lattice of Anderson ions plus a band of uncorrelated electrons, both connected by an hybridization interaction. Each Anderson ion can have a maximum of two electrons, that have a Coulomb repulsion U when both are present, and each ion is described by four local states. The state with double occupation is empty when U® ¥ and can be neglected, and one can use again the Hubbard operators to project out this state, but it is first necessary to extend their definition to many sites. The expansions employed with the usual Fermi or Bose operators are not valid for these operators, and Hubbard introduced for his model of correlated electrons [8] a diagrammatic expansion with cumulants [9] which uses the electron hopping as a perturbation, and becomes the usual expansion when U = 0. In the present work we shall employ an extension of Hubbard's cumulant expansion that is valid for the Anderson lattice [2] and uses the hybridization as perturbation.

When one considers an hypercubic lattice in infinite dimensions, the cumulant expansion gives the exact GF in terms of an unknown effective cumulant. We propose an approximation that uses this expression for a lattice of finite dimensions, and approximates the effective cumulant by employing the known exact solution of the Anderson lattice in the atomic limit, i.e. when the band of uncorrelated electrons has zero width. The spectral density obtained in this approximation is plotted for some typical values of the system parameters, and shows a structure close to the chemical potential m, that affects the physical properties at low temperatures and is absent from the GF derived with other approximations[2].

The conclusions are then presented, and the advantages and problems of the Hubbard operators are discussed.

II. The ionic problem and the Hubbard operators

To motivate the use of the Hubbard operators we shall consider the lowest energy levels of a Co²⁺ impurity in a MgO crystal. The ground configuration of the free Co²⁺ is (3d)⁷, and a basis of the corresponding states could be constructed in Fock space by employing the usual Fermi creation operators. There are 120 states allowed by the exclusion principle[10], and they would be all degenerate if only the electron-nucleus interaction was considered. The Coulomb repulsion introduces a very strong correlation between the electrons, and separates the states into eight spectral terms with different energies, with a ⁴F ground term which is 28 times degenerate. The cubic crystal field splits ⁴F into three spin quadruplets with cubic symmetries T_1g, T_2g and A_2g, and also mixes the T_1g with the excited ⁴P term. The resultant T_1g is the lowest term, and it is further split by the spin orbit interaction into doublets G₆ and G₇ and two quadruplets G₈. These levels are shown in Fig. 1, and all the corresponding states are linear combinations of several Slater determinants. To obtain these states in Fock space it would be necessary to apply rather complicated polynomials of the usual Fermi creation operators to the vacuum, and trying to use many body techniques with the usual creation or destruction operators of the ten possible 3d states would then require the use of the whole space of the (3d)⁷ configuration. The Hubbard operators make it possible to use an arbitrary subspace, e.g. all the states of the ground T_1g term, and the rather complicated electronic correlations of these states would then remain hidden in the properties of these operators. To define them in a general way, consider a subspace E_n of the states of the system that is spanned by the n orthogonal states {| a ñ } that are relevant to a particular problem, where a = 1,2,¼,n. We define the n² Hubbard operators

X_a,b = | a ñ á b| (1)

that transform the state | b ñ into the state |a ñ , i.e. X_a,b| b ñ = | a ñ . In the case of the Co²⁺ impurity we chose the twelve energy eigenstates of the ground T_1g term, and we can then write the corresponding Hamiltonian as

H_Co = å
a E_a X_a,a , (2)

where the subindexes a identify the twelve states of the G₆, G₇ and two G₈ levels shown in Fig. 1. These are the states most relevant to the interaction between the Co²⁺ impurity and the MgO phonons because they have comparable energies, and Eq. (2) will be a part of the total Hamiltonian that is used in the next section to discuss that problem.

Figure 1.
Energy levels of the ground ⁴F term of a Co²⁺ split by a cubic field and by the spin orbit interaction. The levels are labeled by their symmetry properties.

The Hubbard operators do not satisfy the usual commutation or anticommutation relations obeyed by the Fermi or Bose operators, and the best alternative is to use the rules of product:

X_a,b X_c,d = d_b,c X_a,d . (3)

These rules are sufficient to study the properties of the X_a,b.

A. Electronic Raman scattering from Co²⁺:MgO

The Hamiltonian of a Co²⁺ impurity in a MgO crystal, in the presence of the crystal phonons and of a Jahn-Teller interaction between the two systems is, in the absence of radiation,

H = H_Co+H_ph+H_JT , (4)

where H_ph is the Hamiltonian of the phonons, H_Co is that of the Co²⁺ impurity, and the Jahn-Teller interaction is approximately given by

H_JT = V_E( t^q Q_q+t^e Q_e) +¼ . (5)

In this equation, V_E is a coupling constant, Q_q and Q_e are the normal modes of vibration q and e of the complex formed by the Co²⁺ and the six nearest neighbor Oxygen ions[11], and t^q and t^e are the corresponding electronic operators [1,12], all of them associated to the irreducible representation E_g of the cubic group. For simplicity, the part of the interaction corresponding to the symmetric irreducible representations A_1g and T_2g have been left out from Eq. (5). The H_Co is given in Eq. (2) using the X_a,a projection operators, and H_ph can be expressed in terms of the phonon creation (a_qs^f ) and destruction (a_qs) operators of wave vector q and polarization s. In the H_JT we can express the t^q and t^e using Hubbard operators[5], and expand the Q_q and Q_e using the a_qs^f and a_qs[1], so that the Hamiltonian in Eq. (4) is then written as a function of the X_a,b, a_qs^f and a_qs operators.

To calculate the electronic Raman scattering from the Co²⁺ impurity in MgO one can not start from the projected Hamiltonian in Eq. (5), because the photons have much larger energies than the splitting between the levels of the ground term T_1g, and their main interaction is with higher excited states. It is possible to show that the intensity I(w) of the electronic Raman scattering is approximately given[,] by the following expression

I( w) = å
a,b å
c,d ( e^¢·R_a,b·e) ( e·R_c,d·e^¢) ó
õ ¥

-¥ á X_a,b( t) X_d,c ñ exp( -iwt) dt (6)

where w is the frequency of the scattered photon minus that of the incident one, which have polarizations e and e^¢ respectively. The indices a and b correspond to the twelve states of the ground T_1g term of Co²⁺, and the corresponding Raman tensors R_a,b originate in a sum over excited states of frequency dependent terms, the X_a,b( t) is the X_a,b in the Heisenberg representation of the system without radiation, and á A ñ is the statistical average of the operator A in the same system. All the influence of the intermediate states in the time dependent perturbation calculation that gives Eq. (6) appears in the tensors R_a,b and R_c,d, so that in this approximate formula we have been able to separate the effects of radiation from the effects of the interaction between the Co²⁺and the crystal phonons. To calculate á X_a,b( t) X_d,c ñ it is then sufficient to consider only the subspace of states of the ground term T_1g and their interaction with the phonons, described by Eq. (4).

To obtain the á X_a,b( t) X_d,c ñ , we have used the double-time GF[7], following closely the method employed in similar calculations[6, 13]. A closed system was obtained by decoupling the equations of motion and neglecting some of the higher order contributions[5], and the resulting equations were solved for the GF associated to the averages required.

The expression of I( w) obtained by employing these correlation functions was calculated using an analytical density of phonons given by the sum of two continuous curves, which approximates the theoretical curves obtained by Peckham[14] as shown in Fig. 2. These values of I( w) were compared[5] with the experimental results of Guha[15], as shown in Fig. 3 for a particular configuration of the experiment. The differences between the two curves are attributed to the contribution of the one and two-phonon scattering, although it is difficult to separate the two contributions when the transition energies are close, as it is in the present case. The electronic spectra would be given by sharp lines in the absence of the phonon interaction, and the present treatment gives them a shape that is rather more complex than a sum of Lorentzians.

Figure 2.
One-phonon density of states in the MgO: (a) The curves computed by Peckham [14]; (b) the approximation used, where the dotted lines represent the acustic and optical phonon contributions.

Figure 3.
Raman spectra of the MgO:Co²⁺ in the E_g configuration: (a) Electronic contribution as calculated by the present theory; (b) experimental curve obtained by Guha [15] at 18 K.

We can conclude that the use of the Hubbard operators makes possible to solve this problem by using many body techniques in a small subspace of the (3d)⁷ configuration.

III. The Hubbard operators for a lattice

In the previous section the Hubbard operators for the local states were considered at a single site, but the definition of Eq. (1) must be extended when it is necessary to consider several sites. Assume that there are n orthogonal states {| j,a ñ }localized at each site j of the lattice, where j = 1,2,¼,N_s . These states span a space E_j,n at each site j, and it is natural to define the n² Hubbard operators associated to each j:

X_j;a,b = | j,a ñ á j,b| . (7)

The product rules for two operators at the same site are the same given in Eq. (3),

X_j,ab X_j,cd = d_b,c X_j,ad . (8)

but one has more freedom to define the operation when they are at different sites. The trivial assumption would be to assume that the operators commute, and this would not give any problem if all the states had the same number of electrons[13]. When it is necessary to consider states |a ñ and | b ñ differing by an odd number of electrons, it would be rather awkward to adjust the phases of the coefficients so the projected Hamiltonian would correspond to the original model. To avoid this problem, it is then convenient to chose properties as close as possible to those of the usual Fermi or Bose operators. We then say that X_j,ab is of the "Fermi type'' ("Bose type'') when the number of electrons in the two states | j,añ and | j,bñ differ by an odd (even) number and, for j ¹ j^¢, use { X_j,ab X_j^¢,cd} = 0 when the two operators are of the "Fermi type'' and [ X_j,ab X_j^¢,cd] = 0 otherwise.

A. The Anderson lattice for U® ¥

The Anderson lattice gives a schematic description of very important systems with strongly correlated electrons, and there are several reviews devoted to this and closely related problems [16, 17].The Anderson lattice with finite U is described by the Hamiltonian

where C_ks^f (C_ks) is the usual creation (destruction) operator of conduction band electrons with wavevector k and spin component s /2, the f_js^f (f_js) are those corresponding to the local (f) electrons at site j , and

V_j,k,s = V(k)exp( ik.R_j) . (10)

At each site j, the state space of the f-electrons is spanned by four states: the vacuum state | j,0ñ, the two states | j,sñ of one f-electron with spin component s /2 and the state | j,dñ with two electrons of opposite spin. In the limit of infinite electronic repulsion (U® ¥) the state \midj,dñ is empty, and one can consider a reduced space of states by projecting | j,dñ out.

To make the connection with the Hubbard operators one could substitute

into Eq. (9), where the factor s = ±1 is necessary to obtain the correct phase of the states. Eliminating the and X_j,dd one obtains the projection of H into the reduced space:

B. The cumulant expansion

Several methods that employ Hubbard operators have been used to study strongly correlated systems. The decoupling of the equation of motion has been extensively used[8, 18, 19, 20] to study both the Hubbard model and the Anderson lattice. Within perturbation theory, a diagrammatic expansion around the atomic limit has been developed in a series of papers by Keiter, Kimball and Grewe[21, 22, 23] (KKG), and has been fairly successful to treat the Anderson impurity employing the non-crossing approximation[24, 25, 26]. This method is able to interpret all the terms in the expansion as elementary excitation processes, but in the Anderson lattice it has an excluded volume problem that is very hard to treat rigorously[27] and sacrifices the linked cluster expansion[22].

The cumulant expansion has been employed by several authors to study the Ising and the Heisenberg models [28], while Hubbard[9] extended the method to a quantum problem with fermions. In this technique the cumulant averages[29] are used to rearrange the usual perturbative expansion[9], and it is possible to derive a diagrammatic expansion involving unrestricted lattice sums of connected diagrams, that satisfies a linked cluster theorem. This technique was extended to the Anderson lattice[2], and a brief description of the method is given here. This treatment employs the Grand Canonical Ensemble of electrons, and it is convenient to introduce

where m is the chemical potential and n_a is the number of electrons in the state | j,a ñ . The last term in Eq. (12) will be considered as the perturbation, and the exact and unperturbed averages of any operator A are respectively denoted by < A > _H and < A > . It is also convenient to introduce

e_j,a = E_j,a-mn_a (14)

and

e_ks = E_ks-m , (15)

because the energies E_j,a of all ionic states | a > and the energies E_k,s of the conduction electrons appear only in that form in all the calculations.

The Matsubara expansion is employed, so that t is the imaginary time in the GFs á (

_j,a(t)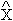 _j^¢,a^¢) ₊ ñ _H that are considered here, and

^
X j,a (t) = exp( tH) X_j,aexp( -tH) . (16)

The subindex + in the definition of the GF indicates that the operators inside the parenthesis are taken in the order of increasing t to the left, with a change of sign when the two Fermi-type operators have to be exchanged to obtain this ordering.

In Fig. 4 some of the infinite diagrams that contribute to á ( 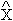_j,a(t) 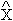_j^¢,a^¢) ₊ ñ _H are shown, and the full circles (f-vertices) correspond to the cumulants of the f-electrons. Each line reaching a vertex is associated to one of the X operators of the cumulant, and the free lines (i.e. those that do not join an empty circle) correspond to the external X operators appearing in the exact GF. An explicit definition of the cumulants can be found in the references [2, 9, 30],and they can be calculated by employing a generalized Wick's theorem[30, 31, 32].

Figure 4.
Typical cumulant diagrams for one-particle GF (a) The diagrams of the chain approximation (CHA) for the f-electron, represented by the filled square to the right, (b) As (a) but for the c-electrons , represented by an empty square. (c) A more complicated diagram, with cumulants of fourth and sixth order.

The first diagram in Fig.4a corresponds to the simplest free propagator á ( X_j,a(t) X_j^¢,a^¢) ₊ ñ , and the second diagram in that figure has an empty circle (c-vertex) that corresponds to the conduction electron cumulant, equal to the free propagator á (C_ks(t) C_ks^f ) ₊ ñ . The interaction is represented by the lines (edges) joining two vertices and, because of the structure of the hybridization, they always join a c-vertex to an f-vertex; the number of edges in a diagram gives its order in the perturbation expansion.

Cumulants containing statistically independent operators are zero, and those appearing in the present formalism (with the hybridization as perturbation) vanish unless they contain only X operators at the same site or only C or C^f operators with the same k and s. The only non-zero c-cumulants are of second order, because the uncorrelated c-operators satisfy Wick's theorem. On the other hand, the f-vertices can have many legs, all corresponding to X operators at the same site, like the fourth and sixth order cumulants appearing in the rather more complicated diagram shown in Fig. 4c.

All the infinite diagrams that contribute to the GF with cumulants of at most second order are shown in Fig. 4a, and this family is the "chain approximation'' (CHA), which gives the exact solution of Eq. ( 9) when there is no Coulomb correlation (U = 0)[2]. When the spin is eliminated from the problem, the Hamiltonian of equation (12) corresponds to a system of two hybridized bands without any Coulomb repulsion (there can be only one or zero f-electrons at each site), and the CHA is again an exact solution. The diagrams of the c-electron propagator in the same approximation are shown in Fig.4b.

In the Feynmann perturbation expansion, Wick's theorem is valid and only second order propagators appear, while the interactions are provided by the Coulomb interaction. In the present treatment, the U disappears in the limit U® ¥ (or is included in the unperturbed Hamiltonian when U is finite), and the correlations appear through the non-zero cumulants of X operators with order greater than fourth, which include propagators of two or more particles. In the Feynmann expansion of the one particle GF, the two particle GF appear in the self-energy, which contains all the correlations.

C. The spectral density of the GF and the occupation numbers

The two one-particle GFs of interest in the Anderson lattice with U® ¥ are

á ( X_j,0s(t) X_j,s0)₊ ñ (17)

which are defined in the interval 0 £ t £ b º 1/T. It is possible to associate a Fourier series to these GFs because of its boundary condition in this variable[2], and the coefficients correspond to the Matsubara frequencies w_n = pn/b (where n are all the positive and negative odd integer numbers). One can also transform the GF to reciprocal space[2] and, because of the invariance against time and lattice translations, they are proportional to quantities G_s(k,w_n). Considering that these coefficients are the values of a function of the complex variable z = w+iy at the points z_n = iw_n it is possible, in the usual way[2], to make the analytic continuation to the upper and lower half-planes of z, obtaining a function G_s(k,z) which is minus the Fourier transform of the double time GFs[7]. If we assume the system to be uniform, the occupation of the local state á X_j,ss ñ = n_j,s does not depend on j, and it is given by

n_s = ó
õ ¥

-¥ r_0s(w) f_T(w) dw , (18)

where

f_T(z) = { 1+exp( b z) } ^-1 (19)

is the Fermi function and

is the spectral density associated to the transition (0,s). With the same r_0s(w) it is also possible to obtain the occupation n₀ of the empty state | 0ñ:

n₀ = ó
õ ¥

-¥ r_0s(w) (1-f_T(w)) dw . (21)

The GF is given in the CHA by

where the energies e₁(k) and e₂(k) are those of the two elementary excitations with wave vector k, resulting from the hybridization of a band e_ks and a dispersionless band of energy e_f = E_js-m, with a reduced hybridization constant . They are given by the two roots of (z-e_f)(z-e_ks)-D_s| V(k)| ² = 0, where

D_s = á X₀₀+X_ss ñ . (23)

The spectral density r_0s(w) is plotted in Fig. 5 as the dotted curve, assuming the following system's parameters: E_j,s = E_f = -0.5, m = 0., T = 0.001, a local hybridization V = 0.3 and a density of states of the unperturbed band electrons given by a rectangular band of width p centered at the origin, all in the same energy units. The spectral density for the unperturbed f-electrons is a d located at e_f = -0.5, and in the CHA it becomes a band with a gap roughly proportional to the reduced hybridization constant and centered at e_f. For these parameters the system is in the "Kondo region'', in which the local state should have nearly the maximum occupation compatible with the paramagnetic state, viz. n_s = 0.5. A narrow temperature dependent peak, the "Kondo peak'', should then appear very close to the chemical potential, i.e. close to w = 0. This missing peak is responsible for many properties of the "heavy fermions''[16], and it is closely related to the minimum in the temperature dependence of resistivity observed in many metals with magnetic impurities. To explain this property is essential to consider spin flip processes[34] which are absent from the CHA because diagrams with only second order cumulants do not include spin flips. The absence of the Kondo peak from the spectral density obtained with the CHA is therefore not surprising, and an attempt to obtain that peak was made by considering diagrams that contain infinite fourth order cumulants[2, 35]. The family of diagrams that was considered is shown in Fig. 6c, but the result was again unsuccessful, as shown by the dashed line in Fig. 5, which is the plot of the spectral density obtained by this approximation for the same parameters used to calculate the dotted line. Two sharp peaks appear inside the gap in this approximation, but they are not related to the Kondo peak, which should appear close to w = 0. A more complex family of diagrams[30, 35], related to the of the F-derivable approximation[28] and to the "conserving approximations'' of Kadanoff and Baym[36], was also attempted, but again without success.

Figure 5.
The spectral density of the f-electrons for a system with the following parameters: E_j,s = E_f = -0.5, m = 0., T = 0.001, a local hybridization V = 0.3 and an unperturbed band of electrons with a rectangular density of states of width p and centered at the origin, all in the same energy units. (a)The dotted curve shows the values obtained with the CHA. (b) The dashed curve gives the values obtained with the "multiple loop approximation'' (MLA), that corresponds to the family of diagrams shown in Fig. 6. No structure is observed close to w = 0., where the Kondo peak should be present.

Figure 6.
The Multiple Loop Approximation (MLA). (a) The family of diagrams with only one fourth order cumulant. (b) Diagrams with infinite fourth order cumulants. (c) The diagrams that give the MLA correction to the GF in the CHA. They should be added to the diagrams in Fig. 4a.

A different type of attempt, that was partially successful is discussed in the next section.

IV. The exact atomic solution as a starting point

The exact solution of the local problem has been already used in different ways to study the Anderson lattice. The limit U® ¥ was studied in the intermediate valence case[37] by considering only the lowest four eigenstates of the local Hamiltonian. These were expressed in terms of two pairs of fermi creation and destruction operators, one for each spin, and the resulting total Hamiltonian showed the electronic correlation through two terms: a Hubbard like interaction and a correlated hopping between sites, which contained four and six fermi operators. The system was then studied by a Hartree Fock decoupling, and the magnetic susceptibility and instabilities were discussed employing the resulting self-consistent Hamiltonian [38]. A similar treatment was employed when the two active configurations are magnetic[39], and it was found that only magnetic states are present at T=0. Considering only the atomic limit, viz. taking E_k,s = E₀, Alascio et.al.[40, 41] studied the model for the whole range of parameters, showing that "most of the essential characteristics'' of these systems "are present in this crudely simplified Hamiltonian''. Simões et.al.[42] employed the atomic limit together with a diagrammatic method[43], that is essentially equivalent to our CHA, considering both the hoping and the hybridization as perturbations. An important improvement of the technique was to apply the same diagrammatic expansion to the exact solution of the atomic limit[44, 45], employing only the hopping as perturbation, and this technique has also been applied to study the problem with finite U.[46, 47]. The approximation proposed here uses an expression for the GF that is exact in the limit of infinite dimension, and is given in terms of an effective cumulant . It then employs the exact solution of the atomic model to replace this quantity by an approximate one, the . This treatment was derived from the diagrammatic expansion[2] that uses the hybridization as perturbation and employs the exact solution of the uncorrelated conduction band. This seems a better starting point than considering the hopping as a perturbation, because the hybridization is usually rather smaller than the bandwidth.

A. The exact solution in the atomic limit

When E_k,s = E₀ and V_j,k,s = V_j,s is a local hybridization, the eigenvalue problem of Eqs. (9) or (12) has an exact solution[37], and the GF can be calculated analytically. As the problem is fully local, one can use the Wannier representation for the creation and destruction operators C_j,s^f and C_j,s of the c-electrons, and write H_r = å_jH_j, where H_j is the local Hamiltonian

H_j = å
s { E₀ C_j,s^fC_j,s+ E_j,s X_j,ss+( V_j,s X_j,0s^f C_j,s+V_j,s^* C_j,s^f X_j,0s) } , (24)

and the subindex j can be dropped because we assume a uniform system.

We shall denote with | n,rñ the eigenstates of the Hamiltonian H_j with eigenvalues E_n,r, where n is the total number of electrons in that state, and r characterizes the different states. These eigenstates satisfy

H | n,rñ = e_n,r | n,rñ , (25)

where H is given in Eq. (13) and e_n,r = E_n,r-nm (cf. Eq. (14)). In Table I we give the properties of the | n,rñ states: number of electrons n, name of the state r, z component of spin S_z and e_n,r = E_n,r-nm. The twelve eigenvalues e_n,r of H_j are represented in Fig. 7, and those corresponding to different occupations n = 0,1,2,3 are drawn in different columns. The states are identified in the figure by the numbers r above the levels, and the lines joining different levels correspond to the possible transitions that contribute to the GF.

Figure 7.
The energies e_n,r = E_n,r-nm of the twelve eigenstates | n,rñ of the atomic limit are represented in this figure, and those corresponding to different occupations n = 0,1,2,3 are drawn in different columns. The index r that characterize the states is written above the corresponding levels, and the lines joining different levels are identified by numbers i, showing the possible transitions u_i that contribute to the GF. As with Eqs. (14 , 15), the frequencies have the chemical potential m subtracted, so that the Fermi surface corresponds to w = 0.

It is now straightforward to express the Fourier transform of the f-electron GF in the form

where

and W = -kTlnåexp(-be_n,r) is the grand canonical potential[48]. The equivalent equations for the c-electrons are obtained by just replacing | án-1,r^¢ | X_0s | n,rñ | ² in Eq. (27) by | án-1,r^¢ | C_j,s | n,rñ | ².

The f-electron GF can be written in the form

where u_i are the poles and m_i the residues of the GF. There are only eight different u_i for the f-electron GF, because different transitions have the same energy and the residues of some transitions are zero. Each u_i = -( e_n-1,r^¢-e_n,r) corresponds to the lines identified with i that appear joining the levels in Fig. 7, the two lines u₁ and the single lines u₃ and u₇ represent transitions that are allowed in the absence of hybridization, while the remaining ones correspond to transitions that are forbidden in that limit. It is important to notice that for a system with given values of E₀, E_f and V, the position of the levels in Fig. 7 changes with the chemical potential m. In that figure we have E₀ = m and E_f < E₀ = m. For that system the ground state is always the singlet \mid 2,9ñ, which has no magnetic moment in the absence of field but can have a rather large induced moment because of the proximity of the magnetic triplet[41].

B. The infinite dimension limit

The approximation discussed in this section was inspired in the fairly recent study of correlated fermions on a lattice in high dimensions. The limit of infinite spatial dimensions (d® ¥) has been applied by Metzner and Vollhardt[49, 50] to strongly correlated fermion systems, providing non-trivial models of the Hubbard type that are substantially simpler to analyze. Considering an hypercubic lattice in infinite dimension, they obtained important simplifications in the diagrammatics of the Hubbard model when the Coulomb repulsion, viz. the U term in Eq. (9), was employed as a perturbation. Metzner [51] revisited the cumulant expansion[9] of the Hubbard model, where the electron hopping is considered as a perturbation, and derived the properties of this expansion when d® ¥. In particular, only the diagrams that are topologically "fully two particle reducible'' (f.t.p.r.) remain in this limit. These diagrams are those in which any pair of vertices can be separated by cutting one or two edges [49], and one should stress that the topology of a diagram can be different from that of its possible embeddings in the lattice, because in the cumulant expansions there is no excluded site restriction in the lattice sums[2], and two different vertices of a diagram can occupy the same site. The property stated above refers to the topology of the embeddings, and in the sum of contributions of diagrams that are not f.t.p.r. there may be terms that give non zero contributions because the topology of their embedding is f.t.p.r.[52]

In the cumulant expansion of the Anderson lattice[2] we employ the hybridization, rather than the hopping, as a perturbation and the exact solution of the conduction problem in the absence of hybridization is included in the zero-th order Hamiltonian. For this reason it was necessary to extend Metzner's derivation[51] to the Anderson lattice [52], and it was shown that the same type of results he obtained are valid for this model.

Employing the cumulant expansion, Metzner has shown[51] that the single-particle properties of the Hubbard model in the limit d®¥, can be described as that of independent electrons "hopping between dressed atoms characterized by an effective Green's function''. A similar derivation can be employed for the Anderson lattice, and the exact one-electron GF is then given by the family of diagrams in Fig. 4a, but using an effective cumulant (z) for the f-electron vertices instead of the bare one M_2,s⁰(z) = -D_s⁰/(z-e_f). The effective cumulant (z) is given by the contribution of all the diagrams of G_s(R_n,m = 0,z) that can not be separated by cutting a single edge (usually called "irreducible diagrams''), where G_s(R_n,m = 0,z) is the exact GF of the f-electrons in the real space representation for n = m, viz. the local GF. This property is only valid in the limit d® ¥, and the only non-zero contributions are of those diagrams that have f.t.p.r. embeddings. The exact GF is then written

A practical difficulty with the cumulant expansions of systems of correlated electron, is that the higher order cumulants rapidly become very laborious to calculate. This difficulty is not alleviated when d® ¥ because all the higher order cumulants remain in this limit, but the equations of the type of Eq. (29), that are valid for different expansions, suggest several approximations, and one should mention the very successful "dynamical mean field theory'' [17]. The approximation presented in the present work do not give results as accurate as this last technique, but has the advantage that its numerical calculation is fairly rapid, and that it can be extended without much difficulty to more complex systems with too many local states, by employing the technique discussed in the present paper of projecting a large space of states into a subspace of interest with the use of Hubbard operators. The proposed approximation is to calculate exactly the effective cumulant (z) for a soluble model closely related to the Anderson lattice, and replace it in Eq. (29) to obtain an approximate GF. The model proposed to obtain the approximate (z) is the atomic limit of the Anderson lattice, that is defined by neglecting the hopping, so that the system is described by the Hamiltonian of Eqs. (9) or (12) but with E_k,s = E₀. In the next section we show how to calculate this approximate effective cumulant, and discuss the spectral densities obtained by this method.

A second approximation that is used in this work, is to employ the Eq (29) for a finite dimensional lattice, although it is only valid for d® ¥. A justification for this procedure is the fact that Schweitzer and Czycholl[53] have shown that the local approximation provides "a good description of three dimensional systems''. They considered the second order perturbation approach of the Anderson lattice, employing the term in U as perturbation and taking the d® ¥ limit as the starting point for a 1/d expansion.

C. The atomic effective cumulant approximation

The atomic effective cumulant approximation (AECA) consists in substituting (z) in Eq. (29) by an approximate (z) derived from the exact solution of the atomic limit. This is obtained by solving for (z) in the equation that is the atomic equivalent of Eq. (29), and one obtains

The (z) is then the effective cumulant, that substituted in Eq. (29), gives the exact (z) in the atomic limit, and from the point of view of the cumulant expansion, it contains all the irreducible diagrams that contribute to the exact (z). It should be emphasized that this diagrams contain loops of any size, because there is no excluded site in this expansion, and all the filled circles correspond to the same site, although they appear as different vertices in the diagram. The difference between the exact and approximate quantities is that different energies E_k,s appear in the c-electron propagators of the effective cumulant (z), while these energies are all equal to E₀ in (z). Although (z) is for that reason only an approximation, it contains all the diagrams that should be present, and one would expect that the corresponding GF would show fairly realistic features.

One still has to decide what fixed value of E₀ should be taken. As the most important region of the conduction electrons is the Fermi energy, we shall use E₀ = m, at least when m is inside the conduction band.

Another important point, is that concentrating all the conduction electrons at E₀ would overestimate their effect, and we shall then reduce the hybridization by a coefficient that gives the relative number of c-electrons that most contribute. We consider that this region is of the order of Vr₀, where r₀ is the density of states of the unperturbed c-electrons with respect to the energy, and to be more definite we chose pVr₀, so the effective hybridization constant V_a coincides with the usual "mixing strength'' D = pV²r₀. This is essentially the same choice made by Alascio et.al.[40] in their localized description of valence fluctuations. Note that V_a is only used in the calculation of (z), and that the full value must be substituted in the V that appears explicitly in Eq. (29), because the whole band of conduction energies is used in (k,z) = -1/( z-e_ks) .

Other consequence of the use of a single energy for the calculation of (z) is that the spectral densities show rather sharp features, and to alleviate this behavior we have employed a small imaginary part ih to the z of Eq. (30). Note that the imaginary part h of the variable z in the calculated spectral densities does not have to be equal to h_a, and we usually choose h << h_a: the typical values we employed were h = 10^-4 vs. h_a = 0.003, but we have also used much smaller h without any problem.

The spectral density r_f for several values of T is shown in Fig. 8, while the remaining parameters are the same employed in Fig. 5. The localized energy E_f of the local state is well below the Fermi surface, corresponding to a typical Kondo region. The spectral density r_f does not change with T below a certain value, which is approximately T = 10^-3 in Fig. 8, because below this T the state | n = 2,r = 9ñ is the only occupied in the atomic limit and therefore the (z) does not change. Other states are occupied at higher T, and the changes in (z) are reflected in the r_f. At the lowest T the r_f obtained by the AECA is basically the same of the CHA (cf. Fig. 5) in the region close to e_f = -0.5, but it also has a structure close to the Fermi surface, i.e. at w = 0. Although the peak is not too sharp, it has some of the characteristics of the Kondo peak: its localization and the decrease of its intensity when T increases, as shown in more detail in Fig. 9. This structure shows a pseudo gap, as was obtained by other methods[20, 54], but with a peak below the Fermi energy that is not as sharp. The structure is more complex at higher T , and I believe that this behaviour is due to the use of the atomic model to estimate the (z). The dependence of the spectral density with m is shown in Fig. 10, where the main structure follows the e_f and the structure that corresponds to the Kondo peak remains fixed at the Fermi surface while the system is in the Kondo region, i.e. when e_f < 0. When e_f approaches the Fermi surface the two structures merge, and for e_f > 0 a single structure follows e_f in the intermediate valence region.

Figure 8.
The spectral density r_f(w) of the f-electrons obtained with the AECA for several values of T, employing z = w+ih with h = 10^-4. The system has the following parameters: E_f = -0.5, m = 0., T = 0.001, a local hybridization V = 0.3 and a density of states of the unperturbed band electrons given by a rectangular density of states of width p centered at the origin, all in the same energy units. The effective cumulant was calculated employing a reduced hybridization V_a = D = V² and a frequency with a small imaginary part h_a = 0.003.

Figure 9.
The spectral density of figure Fig. 8 in the neighborhood of w = 0. The integrated intensity of this structure decreases with T.

Figure 10.
The spectral density of the f-electrons for the same system of Fig. 8 but with fixed T = 0.001 and for several values of the chemical potential m. It shows the crossover from the Kondo region to the intermediate valence region.

The AECA gives a r_f that roughly agrees with the results obtained by other methods [20], but the details of the spectral density near the Kondo resonance depend in a very delicate way on the behaviour of M_2,s^eff(z) near that region. In the calculation of M_2,s^at(z) all the band structure is replaced by a single value E₀, and it is therefore not surprising that the AECA results are less precise than those of reference [20], which uses the decoupling of the equations of motion followed by the self-consistent determination of the averages resulting from that procedure. This last method, as well as the dynamical mean field theory [16], require some heavy computation while the AECA is fairly simple from that point of view. As the spectral density r_f in the AECA has the same overall behaviour shown by the methods mentioned above, I believe that it can be used to obtain rather reasonable values of many physical properties and of their dependence with T and other parameters. The main interest in this method, is that it is very natural to make the extension to more complex systems with numerous local states, that can be simplified by using the Hubbard operators to project the Hamiltonian to a subspace of states of interest. The use of the AECA would then make it possible to calculate properties of those systems without employing too heavy computation.

V. Conclusions

In the description with the usual creation and destruction operators of systems that have strongly correlated local states, a large number of states that are not essential to the problem is usually introduced. The purpose of this work is to show how, by employing Hubbard operators, one can project out these irrelevant states and still use many body techniques.

The Hubbard operators can represent complex local states with a simple notation, and the typical example of a Co²⁺ impurity in a MgO crystal was discussed. The 3d⁷ configuration of these ion has 120 states at the impurity site, and we have shown how to reduce the problem of the electronic Raman scattering of Co²⁺ to the calculation of time averages of Hubbard operators in the subspace of the 12 lowest energy states of this ion. These averages were calculated by employing the double time GF of Zubarev, and the resulting scattering intensity was compared with the experimental results.

A second example, that requires Hubbard operators at all the crystal sites, is the Anderson lattice. This model gives a schematic description of very important systems with strongly correlated electrons, like transition metal compounds and systems with anomalous rare earth ions that show intermediate valence or Kondo behavior, heavy fermions, and is also closely related to descriptions of systems with high T_c superconductivity.

When the Hubbard operators are used to describe the Anderson lattice with U® ¥, it is possible to reduce the number of local states at each site from 4 to 3. One may think that this is a meager reduction for all the troubles it causes, but the interest of this study is to learn the technique, that can be applied to rather more complex systems, like metallic compounds with transition metals ions with several d electrons or with rare earths like Eu, Tm, etc. There are several methods to deal with Hubbard operators in the Anderson lattice and related models, and in this work we discussed the cumulant expansion, a technique that was originally applied by Hubbard to the fermion case. The advantages of this technique are that it seems to be the natural extension of the usual diagrammatic techniques, it has no problems of excluded site in the lattice summations and that a linked cluster theorem for the grand canonical potential can be derived. As the Hubbard operators hide in their definition all the electronic correlation of the states they describe, their diagrammatic expansions are more complicated than the ones that employ the usual creation and destruction operators. The main problem is the difficulty of calculating higher order cumulants, and in our work we have only used second and fourth order cumulants. The sixth order cumulants are very laborious to calculate, and we have not been able to use them yet.

One problem with the results we obtained for the Anderson lattice was the absence of a Kondo peak, that should be present in the spectral density of the one-particle GF when the system is in the Kondo region, i.e. when e_f is rather below the Fermi surface. To obtain the particular properties of the Kondo systems it is necessary to consider spin-flip processes in the calculation, and these are absent from the second order cumulants but are present in the fourth order cumulants. As we have considered diagrams with infinite number of fourth order cumulants, it is not clear why the Kondo peak was still absent from our calculations, and we are further studying this problem by considering different types of diagrams with cumulants of that order.

The study of systems in a real space of very large dimensions d has been recently applied with success to the problems of correlated electrons, and we have studied the cumulant expansion of the Anderson lattice for d® ¥. The exact one-electron GF can then be expressed in terms of an effective cumulant (z), that includes diagrams with cumulants of any order, so the same limitation on the calculation of higher order cumulants is present in its calculation. To avoid this problem, the atomic effective cumulant approximation (AECA) was proposed, and it consists in replacing (z) by the corresponding quantity of a related soluble model. This model is the Anderson lattice in the atomic limit, i.e. eliminating the conduction electron hopping by taking a conduction band of zero width. The quantity (z) obtained by this procedure is introduced in the exact formula to calculate the approximate GF. The spectral density r_f obtained with this GF was calculated, and when the system is in the Kondo region it shows a structure close to the Fermi surface. This structure has some of the characteristics of the Kondo peak, viz. its position very close to the Fermi surface and its decreasing intensity when T increases, but it is probably not as good an approximation as those already obtained by other methods, like the decoupling of the equation of motion. Nevertheless, as it has the expected overall behaviour, I believe that it can be used to obtain rather reasonable values of many physical properties and of their dependence with T and other parameters. As the computation required for this method is fairly simple, it would be useful to calculate properties of more complex systems that would require too heavy computation if more precise methods were employed.

References

[1]
• L. T. Peixoto and M. E. Foglio, Revista Brasileira de Física 13, 564 (1983)
[2]
• M. S. Figueira, M. E. Foglio and G. G. Martinez, Phys. Rev. B 50, 17933 (1994)
[3]
• J. Hubbard, Proc. R. Soc. London, Ser. A 285, 542 (1965)
[4]
• S. B. Haley and P. Erdos, Phys. Rev. B 5, 1106 (1972)
[5]
• L. T. Peixoto and M. E. Foglio, Phys. Rev. B 32, 2596 (1985)
[6]
• M. E. Foglio, J. Raman Spectrosc. 10, 52 (1981)
[7]
• D. N. Zubarev, Usp. Fiz. Nauk. 71, 71 (1960) [Sov. Phys.-Usp. 3, 320 (1960)]
[8]
• J. Hubbard, Proc. R. Soc. London, Ser. A 276, 238 (1964)
• J. Hubbard, Proc. R. Soc. London, Ser. A 277, 237 (1964)
• J. Hubbard, Proc. R. Soc. London, Ser. A 281, 401 (1964) (these are the first three papers of a series of six)
[9]
• J. Hubbard, Proc. R. Soc. London, Ser. A 296, 82 (1966)
[10]
• E. U. Condon and G. H. Shortley The Theory of Atomic Spectra (Cambridge: University Press, 1957)
[11]
• U. Opik and M. H. L. Pryce, Proc. R. Soc. London, Ser. A 238, 425 (1957)
[12]
• F. S. Ham, W. N. Schwarz and M. C. O Brien, Phys. Rev. 185, 548 (1969)
[13]
• M. E. Foglio, J. Phys. C: Solid State Phys. 11, 4171 (1978)
[14]
• G. Peckham, Proc. Phys. Soc. London 90, 657 (1967)
[15]
• S. Guha, Phys. Rev. B 21, 5808 (1980)
[16]

• A. C. Hewson, The Kondo problem to Heavy Fermions (Cambridge U.P. Cambridge, 1993)

  P. Schlottmann, Phys.Rep. 181, 1 (1989)

  P. Fulde, Solid State Physics 41, 1 (1988)

  P. A. Lee, T. M. Rice, J. W. Serene, L. J. Sham and J. W. Wilkins, Comments Cond. Mat. Phys. 12, 99 (1986).

[17]
• A. Georges, G. Kotliar, W. Krauth and M. J. Rozenberg, Rev. Mod. Phys. 68, 13 (1996)
[18]
• A. E. Ruckenstein and S. Schmitt Rink, Phys. Rev. B 38, 7188 (1988)
[19]
• M. E. Foglio, Phys. Rev. B 43, 3129 (1991)
[20]
• H. Kaga, H. Kubo and T. Fujiwara, Phys. Rev. B 37, 341 (1988)
[21]
• H. Keiter and J. C. Kimball, Int. J. Magn. 1, 233 (1971)
[22]
• N. Grewe and H. Keiter, Phys. Rev. B 24, 4420 (1981)
[23]
• H. Keiter and G. Morandi, Phys.Rep. 109, 227 (1984)
[24]
• N. Grewe, Z. Phys. B 53, 271 (1983)
[25]
• Y. Kuramoto, Z. Phys. B 53, 37 (1983)
[26]
• T. K. Lee and F. C. Zhang, Phys. Rev. B 30, 1556 (1984)
[27]
• N. Grewe, T. Pruschke and H. Keiter, Z. Phys. B 71, 75 (1988)
[28]
• M. Wortis, in Phase Transitions and Critical Phenomena , edited by C. Domb and M. S. Green (Academic,London, 1974), Vol. 3, pg.113.
[29]
• R. Kubo, J. Phys. Soc. (Jpn.) 17, 1100 (1962)
[30]
• M. S. Figueira and M. E. Foglio, J. Phys.: Condens. Matter 8, 5017 (1996)
[31]
• A. C. Hewson, J. Phys. C: Solid State Phys. 10, 4973 (1977)
[32]
• D. H. Y. Yang and Y. L. Wang Phys. Rev. B 10, 4714 (1975)
[33]
• J. W. Negele and H. Orland Quantum Many-Particle Systems (Addison-Wesley, New York, 1988), Chap. 2.
[34]

• J. Kondo, Progr. Theor. Phys. 32, 37 (1964)

  J. Kondo, Solid State Physics 23, 184 (1969)

[35]
• M. S. Figueira, Doctoral Thesis (Campinas, SP, Brasil: Universidade Estadual de Campinas, 1994 )
[36]

• G. Baym and L. P. Kadanoff, Phys. Rev. 124, 287 (1961)

  G. Baym, Phys. Rev. 127, 1391 (1962)

[37]
• M. E. Foglio and L. M. Falicov, Phys. Rev. B 20, 4554 (1979)
[38]
• M. E. Foglio, C. A. Balseiro and L. M. Falicov, Phys. Rev. B 20, 4560 (1979)
[39]
• P. Schlottmann and L. M. Falicov, Phys. Rev. B 23, 5916 (1981)
[39]
• B. Alascio, R. Allub and A. A. Aligia, Z. Phys. B 36, 37 (1979)
[40]
• A. Alascio, R. Allub and A. A. Aligia, J. Phys. C: Solid State Phys. 13, 2869 (1980)
[41]
• A. S. R. Simões, J. R. Iglesias and E. V. Anda, Phys. Rev. B 29, 3085 (1984)
[42]
• E. V. Anda, J. Phys. C: Solid State Phys. 14, L1037 (1981)
[43]
• A. S. R. Simões, J. R. Iglesias, A. Rojo and B. Alascio, J. Phys. C: Solid State Phys. 21, 1941 (1988)
[44]
• A. S. R. Simões, Doctoral Thesis (Porto Alegre, RS, Brasil: Universidade Federal de Rio Grande do Sul, 1986 )
[45]
• L. G. Brunet, R. Ribeiro-Teixeira and J. R. Iglesias, Sol. Stat. Comm. 68, 477 (1988)
[46]
• L. G. Brunet, M. A. Gusmão and J. R. Iglesias, Phys. Rev. B 46, 4520 (1992)
[47]
• G. G. Martinez Pino, Doctoral Thesis (Campinas, SP, Brasil, Universidade Estadual de Campinas, 1989).
[48]
• W. Metzner and D. Vollhardt, Phys. Rev. Lett. 62, 324 (1989)
[49]
• E. Muller Hartmann, Z. Phys. B 74, 507 (1989)
[50]
• W. Metzner, Phys. Rev. B 43, 8549 (1991)
[51]
• M. E. Foglio and M. S. Figueira, J. Phys. A (1997) to be published
[52]
• H. Schweitzer and G. Czycholl, Sol. Stat. Comm. 74, 735 (1990)
[53]
• N. Grewe, Sol. Stat. Comm. 50, 19 (1984)

• [7] D. N. Zubarev, Usp. Fiz. Nauk. 71, 71 (1960) [Sov. Phys.-Usp. 3, 320 (1960)]
•   J. Hubbard,  Proc. R. Soc. London, Ser. A 277, 237 (1964)
•   J. Hubbard,  Proc. R. Soc. London, Ser. A 281, 401 (1964) (these are the first three papers of a series of six)
• [16] A. C. Hewson, The Kondo problem to Heavy Fermions (Cambridge U.P. Cambridge, 1993) P. Schlottmann, Phys.Rep. 181, 1 (1989)
• P. Fulde,  Solid State Physics 41, 1 (1988)
• P. A. Lee, T. M. Rice, J. W. Serene, L. J. Sham and J. W. Wilkins, Comments Cond. Mat. Phys. 12, 99 (1986).
• [34] J. Kondo, Progr. Theor. Phys. 32, 37 (1964) J. Kondo, Solid State Physics 23, 184 (1969)
• [36] G. Baym and L. P. Kadanoff, Phys. Rev. 124, 287 (1961) G. Baym,  Phys. Rev. 127, 1391 (1962)

Publication Dates

• Publication in this collection
  14 June 1999
• Date of issue
  Dec 1997

History

• Received
  15 Apr 1997