Abstract
We present a review of some applications of quantum field theory in the physics of condensed matter stressing the extremely fruitful interaction between these two areas. The examples considered include the Kondo effect, Polymers, High-Tc superconductivity and Spin Glasses.
Field theory and condensed matter: account of a successful interaction
E. C. Marino
Instituto de Física
Universidade Federal do Rio de Janeiro
Cx.P. 68528, Rio de Janeiro RJ 21945-970, Brazil
E-Mail address: marino@if.ufrj.br
Received January 7, 2000
We present a review of some applications of quantum field theory in the physics of condensed matter stressing the extremely fruitful interaction between these two areas. The examples considered include the Kondo effect, Polymers, High-T
c
superconductivity and Spin Glasses.
I. Introduction
Quantum Field Theory has always been extremely successful in the description of the basic interactions of nature and in the realm of particle physics. Two periods are especially remarkable: the first one with the maturity of QED, after renormalization was understood and the second one with the advent of non-Abelian gauge theories and the corresponding description of the strong and electroweak interactions. Since the beginning of the 80's, however, with the failure of the grand unified theories, other areas of application of Field Theory became more prominent in the edge of the investigation endeavor. One of these is Condensed Matter Physics. Nearly at the same time, some of the most important discoveries of the last two decades have been made, namely: high-temperature superconductivity and the quantum Hall effect. These phenomena and others became major fields of application of QFT. In this article, we make an extremely incomplete review of some interesting applications of field theory in Condensed Matter systems, as well as describe the fruitful interchange of ideas between the two areas.
II. The Kondo Effect
The Kondo effect is observed when we introduce magnetic atoms at very low concentrations in a non-magnetic metal and consist in a series of anomalies appearing in the magnetization, resistivity and impurity magnetic susceptibility as a function of the temperature. The interaction among the electrons of the metal and the impurities is magnetic and can be simulated by the chiral Gross-Neveu interaction in 1+1D,
where y is the electron field, c is the impurity field. The first and second terms between parentheses are, respectively, the electron and impurity spin operators.
This model has been exactly solved for the spectrum through the Bethe ansatz whereby the free energy can be evaluated. The thermodynamic properties thereby obtained are in good agreement with the experiment. The remarkable fact is the dynamical generation of a scale, the Kondo temperature TK, separating a strong and a weak coupling regimes exactly as in QCD, a scale is dynamically generated separating the asymptotic freedom and confining regimes.
III. Polymers: Polyacethilene
Polyacethilene is a quasi one dimensional chain of CH radicals bound by alternating single and double bonds [8]. There are two degenerate ground states, or dimerizations, corresponding to the double bond being either to the left or to the right of a given radical. The system has one electron per site and therefore in the tight binding approximation, it would be a metal. However, the interaction of the electrons with the lattice changes the situation. This interaction is of the form
where y is the electron field, f is the phonon field and the second term in the elastic lattice energy.
If we integrate over f we obtain the familiar simple Gross-Neveu model. On the other hand, integrating over the fermion field, we get an effective action for the scalar field f, which has two degenerate minima ± f0, corresponding to the two dimerizations mentioned above. Shifting f around any of these minima, according to (2) would lead to the dynamical generation of a mass for the y field or, equivalently, to the generation of a gap for the electrons, thereby explaining the insulating character of polyacethilene. This is the so called Peierls mechanism, which in field theory language corresponds to the dynamical mass generation which is used, for instance in the Weiberg-Salam-Glashow unified theory for the weak and electromagnetic interactions. There are soliton solutions interpolating the two minima of the effective f potential. These are defects on the polymer lattice.
IV. Confinement in QCD: Dual Meissner Effect
Confinement is one of the most interesting phenomena in physics. It has remained somewhat mysterious for some time even though quarks can be observed inside hadrons exactly in the same way nuclei have been observed inside atoms through the scattering experiments performed by Rutherford and collaborators in the beginning of the century.
In condensed matter, however, there is a phenomenon closely related to confinement. This is the well known Meissner effect occurring in type II superconductors. In these, an applied magnetic field is expelled from the bulk material, except for a number of magnetic fluxes confined in tubes. A pair of magnetic monopoles placed on the extremities of these tubes would be confined exactly as quarks inside a hadron because the potential corresponding to such flux tubes rises linearly with the distance. Hence, we may understand quark confinement in QCD as a dual Meissner effect.
V. High Temperature Superconductors
There is by now clear experimental evidence [1, 2, 3, 4] that the pure high-Tc superconductor cuprates are well described by a quasi two-dimensional Heisenberg antiferromagnet on a quasi-square lattice, whose sites are occupied by Cu++ magnetic ions. The ground state is the antiferromagnetically ordered Néel state. In the continuum approximation, the system can be described by the O(3) nonlinear sigma model formulated in a two-dimensional space which is the continuum version of the original lattice [5], the ordered magnetization of the spins corresponding to the nonlinear sigma field na, (a = 1, 2, 3).
The nonlinear sigma field is the continuum limit of the ordered magnetization of the antiferromagnetic Heisenberg model describing the active electrons of the Cu++ magnetic ions of a pure high-Tc cuprate. It satisfies the constraint nana =  , where
, where  is such that
is such that  , S being the spin quantum number, c the spin-wave velocity and a, the lattice spacing. Using linear spin-wave theory results for the Heisenberg model, on the other hand, it is found that
, S being the spin quantum number, c the spin-wave velocity and a, the lattice spacing. Using linear spin-wave theory results for the Heisenberg model, on the other hand, it is found that  = 1.18(2S)
= 1.18(2S)  J where J is the Heisenberg antiferromagnetic coupling constant. These two relations are valid for large S. Assuming the ratio of both holds for any S and, in particular for S = 1/2, which is the relevant case here, we establish the following relation between the coupling constants in the continuum and in the lattice,
J where J is the Heisenberg antiferromagnetic coupling constant. These two relations are valid for large S. Assuming the ratio of both holds for any S and, in particular for S = 1/2, which is the relevant case here, we establish the following relation between the coupling constants in the continuum and in the lattice,
The field na is conveniently expressed in the so called CP1 language in terms of a doublet of complex scalar fields zi, (i = 1, 2) subject to the constraint  zi =
zi =  , through
, through
where sa are Pauli matrices. In this language, the continuous field theory corresponding to the Heisenberg antiferromagnet is described by the lagrangian density in two spatial dimensions [5, 6]
where Dm = ¶m + i 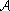 m and
m and 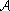 m =
m =  (i
(i ¶zi).
¶zi).
The CP1-nonlinear sigma model possesses classical topologically nontrivial solutions called skyrmions [7]. These bear one unit of the topological charge Q = òd2x J0, where Jm is the identically conserved topological current. In terms of the CP1 field 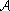 m, this is given by Jm =
m, this is given by Jm =  emab¶a
emab¶a
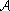 m along the plane. This means that, in the CP1 language, the skyrmions are
m along the plane. This means that, in the CP1 language, the skyrmions are 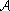 m-"magnetic" vortices. In the original Heisenberg model version, on the other hand, they are defects (textures) upon the ordered Néel state. We shall use a general method of vortex quantization [9, 10] to the skyrmions/vortices of the continuous theory describing the superconducting cuprates. This method allows for the explicit construction of a vortex/skyrmion creation operator m(x) and the subsequent evaluation of its correlation functions.
m-"magnetic" vortices. In the original Heisenberg model version, on the other hand, they are defects (textures) upon the ordered Néel state. We shall use a general method of vortex quantization [9, 10] to the skyrmions/vortices of the continuous theory describing the superconducting cuprates. This method allows for the explicit construction of a vortex/skyrmion creation operator m(x) and the subsequent evaluation of its correlation functions.
We now propose a model for the process of doping. For this purpose, we already start with the continuum language and associate to the electron/hole dopants a two-component Dirac field with two internal indices corresponding to the two possible spin orientations: ya (x), a =  , ¯. For YBa2Cu3O6+d the Fermi surface with dopants has an almost circular shape [2] and expanding around it we can use a relativistic approximation for the dispersion relation of the dopants. This is clearly not valid for La2-dSrdCuO4 because of the shape of the Fermi surface [2]. We propose the following lagrangian density for describing the dopants and their interaction with the background lattice in YBa2Cu3O6+d
, ¯. For YBa2Cu3O6+d the Fermi surface with dopants has an almost circular shape [2] and expanding around it we can use a relativistic approximation for the dispersion relation of the dopants. This is clearly not valid for La2-dSrdCuO4 because of the shape of the Fermi surface [2]. We propose the following lagrangian density for describing the dopants and their interaction with the background lattice in YBa2Cu3O6+d
In the above expression, m* and vF are, respectively, the effective mass and Fermi velocity of dopants. This must be supplemented by the CP1 constraint  zi =
zi =  . The dopant dispersion relation corresponding to (5.4) is e(p) =
. The dopant dispersion relation corresponding to (5.4) is e(p) =  which agrees with the fact that the system is still an insulator even after the inclusion of some doping. The spin of the dopants is
which agrees with the fact that the system is still an insulator even after the inclusion of some doping. The spin of the dopants is  . Notice that the ordered spin of the Cu++ electrons is given by (5.2) and their coupling to the
. Notice that the ordered spin of the Cu++ electrons is given by (5.2) and their coupling to the 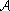 m-field is described by the minimal interaction
m-field is described by the minimal interaction 
 . This suggests, accordingly, the minimal coupling of the dopants to
. This suggests, accordingly, the minimal coupling of the dopants to
The doping parameter d is introduced by means of a constraint identifying the fermion current  igmyi with the dopant current which is given by Dm = d
igmyi with the dopant current which is given by Dm = d  dxmd3(z-x) for a dopant introduced at the point X = (
dxmd3(z-x) for a dopant introduced at the point X = ( , T) and moving along the line L. The 0th-component, for instance, is D0 (
, T) and moving along the line L. The 0th-component, for instance, is D0 ( , t) = d d2 (
, t) = d d2 ( -
-  (t)). The above constraint can be implemented by integration over a vector Lagrange multiplier field lm coupled as
(t)). The above constraint can be implemented by integration over a vector Lagrange multiplier field lm coupled as
¿From the present model we infer [11] that through doping, skyrmion defects are created upon the ordered Néel background in points whose position coincides with that of the dopants. A similar situation occurs in polyacethilene where the doping process produces the formation of soliton defects on the chain [8].
Evaluation of the skyrmion correlation function allows one to extract the skyrmion energy as a function of the doping parameter [11]:
The skyrmion energy is an order parameter for the antiferromagnetic order and we therefore conclude that the Néel state is destroyed for a critical doping parameter
which corresponds to a vanishing skyrmion energy. The experimental values of the Heisenberg coupling constant and spin-wave velocity for YBa2Cu3O6+d are, respectively, J = 100 ± 20 meV [13, 2], and c = 1.0 ± 0.05  [4, 2]. >From J, we get
[4, 2]. >From J, we get  through (5.1). The only remaining input is the dopant lattice spacing. Experimental evidence [14, 1, 2] indicates that the doped holes go into the oxygen p-orbitals. Hence, the dopant lattice parameter is the spacing between the oxygen ions in the CuO2-planes, which for this compound, is aD = 2.68 Å. Entering these data and the numerical value of g in (5.7) we get dC = 0.39 ± 0.03 [11]. This agrees with the experimental value of the critical doping at zero temperature [4], namely, dCexp = 0.41 ± 0.02.
through (5.1). The only remaining input is the dopant lattice spacing. Experimental evidence [14, 1, 2] indicates that the doped holes go into the oxygen p-orbitals. Hence, the dopant lattice parameter is the spacing between the oxygen ions in the CuO2-planes, which for this compound, is aD = 2.68 Å. Entering these data and the numerical value of g in (5.7) we get dC = 0.39 ± 0.03 [11]. This agrees with the experimental value of the critical doping at zero temperature [4], namely, dCexp = 0.41 ± 0.02.
We conclude that our field theory model provides a good description for the normal antiferromagnetic phase of high-temperature superconductors. We are presently investigating extensions of the model to describe higher doped phases.
VI. Conclusion
We conclude that nowadays condensed matter is one of the most important areas of application of quantum field theory. There are many examples where the interaction has been intense with many mutual benefits. Additional systems not mentioned here where interesting applications have been made are: quantum Hall effect, vortices in superconductors and superfluids, magnetic systems among others.
Acknowledgment
This work was partially supported by CNPq and FAPERJ.
References
[1] E. Dagotto, Rev. Mod. Phys. 66, 763 (1994).
[2] A.P. Kampf, Phys. Rep. 249, 219 (1994).
[3] J.M. Tranquada and G. Shirane, in Dynamics of Magnetic Fluctuations in High-Temperature Superconductors, G.Reiter, P.Horsch and G.C.Psaltakis, eds., Plenum, New York (1991).
[4] J. Rossat-Mignod, L.P. Regnauld, J.M. Jurguens, P. Burlet, J.Y. Henry, G. Lapertot and C. Vettier, in Dynamics of Magnetic Fluctuations in High-Temperature Superconductors, G.Reiter, P.Horsch and G.C. Psaltakis, eds., Plenum, New York (1991).
[5] F.D.M. Haldane, Phys. Rev. Lett. 50, 1153 (1983); Phys. Lett. A 93, 464 (1983).
[6] A.M. Polyakov, Gauge Fields and Strings, Harwood, New York (1987); R. Rajaraman, Solitons and Instantons, North Holland, Amsterdam (1982).
[7] A.A. Belavin and A.M. Polyakov, JETP Lett. 22, 245 (1975).
[8] H.Takayama, Y.R. Lin-Liu and K. Maki, Phys. Rev. B 21, 2388 (1980); W. Su, J.R. Schrieffer and A.J. Heeger, Phys. Rev. B 22, 2099 (1980); J. Goldberg et al., J. Chem. Phys. 70, 1132 (1979); S. Ikehata, J. Kaufer, T. Woerner, A. Pron, M.A. Druy, A. Sivak, A.J. Heeger and A.G. MacDiarmid, Phys. Rev. Lett. 45, 1123 (1980).
[9] E.C. Marino, Phys. Rev. D 38, 3194 (1988)
[10] E.C. Marino, Int. J. Mod. Phys. A 10, 4311 (1995)
[11] E.C. Marino, Phys. Lett. A 263, 446 (1999).
[12] E.C. Marino, Phys. Rev. B 61, 1588 (2000)
[13] S. Shamoto, M. Sato, J.M. Tranquada, B.J. Sternlieb and G. Shirane, Phys. Rev. B 48, 13817 (1993).
[14] N. Nücker, J. Fink, J.C. Fuggle, P.J. Durham and W.M. Temmerman, Phys. Rev. B 37, 5158 (1988).
- [1] E. Dagotto, Rev. Mod. Phys. 66, 763 (1994).
- [2] A.P. Kampf, Phys. Rep. 249, 219 (1994).
- [3] J.M. Tranquada and G. Shirane, in Dynamics of Magnetic Fluctuations in High-Temperature Superconductors, G.Reiter, P.Horsch and G.C.Psaltakis, eds., Plenum, New York (1991).
- [4] J. Rossat-Mignod, L.P. Regnauld, J.M. Jurguens, P. Burlet, J.Y. Henry, G. Lapertot and C. Vettier, in Dynamics of Magnetic Fluctuations in High-Temperature Superconductors, G.Reiter, P.Horsch and G.C. Psaltakis, eds., Plenum, New York (1991).
- [5] F.D.M. Haldane, Phys. Rev. Lett. 50, 1153 (1983);
- Phys. Lett. A 93, 464 (1983).
- [6] A.M. Polyakov, Gauge Fields and Strings, Harwood, New York (1987);
- R. Rajaraman, Solitons and Instantons, North Holland, Amsterdam (1982).
- [7] A.A. Belavin and A.M. Polyakov, JETP Lett. 22, 245 (1975).
- [8] H.Takayama, Y.R. Lin-Liu and K. Maki, Phys. Rev. B 21, 2388 (1980);
- W. Su, J.R. Schrieffer and A.J. Heeger, Phys. Rev. B 22, 2099 (1980);
- J. Goldberg et al., J. Chem. Phys. 70, 1132 (1979);
- S. Ikehata, J. Kaufer, T. Woerner, A. Pron, M.A. Druy, A. Sivak, A.J. Heeger and A.G. MacDiarmid, Phys. Rev. Lett. 45, 1123 (1980).
- [9] E.C. Marino, Phys. Rev. D 38, 3194 (1988)
- [10] E.C. Marino, Int. J. Mod. Phys. A 10, 4311 (1995)
- [11] E.C. Marino, Phys. Lett. A 263, 446 (1999).
- [12] E.C. Marino, Phys. Rev. B 61, 1588 (2000)
- [13] S. Shamoto, M. Sato, J.M. Tranquada, B.J. Sternlieb and G. Shirane, Phys. Rev. B 48, 13817 (1993).
- [14] N. Nücker, J. Fink, J.C. Fuggle, P.J. Durham and W.M. Temmerman, Phys. Rev. B 37, 5158 (1988).
Publication Dates
-
Publication in this collection
07 Jan 2002 -
Date of issue
June 2000
History
-
Received
07 Jan 2000










