Fierz-Pauli higher derivative gravity

Abstract

We consider a model for gravity in which the linear part of the four-derivative terms <FONT FACE=Symbol>ò</FONT>R<FONT FACE=Symbol>mn</FONT> R<FONT FACE=Symbol>mn</FONT> <img src="http:/img/fbpe/bjp/v30n3/11eq01.gif" border="0" align="absmiddle">d4 x and <FONT FACE=Symbol>ò</FONT>R² <img src="http:/img/fbpe/bjp/v30n3/11eq01.gif" border="0" align="absmiddle">d4 x are included into the Fierz-Pauli gravitational action. Unitarity is discussed at the tree-level. The issue of the gravitational deflection of a light ray is also considered.

Fierz-Pauli higher derivative gravity

A. Accioly⁽¹⁾, S. Ragusa⁽²⁾, H. Mukai⁽³⁾, and E. de Rey Neto⁽¹⁾

⁽¹⁾ Instituto de Física Teórica,

Universidade Estadual Paulista, Rua Pamplona 145, 01405-900 São Paulo, SP, Brazil

⁽²⁾ Departamento de Física e Informática,

Instituto de Física de São Carlos,

Universidade de São Paulo, C.P. 369,

13560-250 São Carlos, SP, Brazil

⁽³⁾ Departamento de Física,

Fundação Universidade Estadual de Maringá,

Av. Colombo 5790, 87020-900 Maringá, PR, Brazil

e-mail: [e-mail]

Received 20 December, 1999. Revised version received on 31 May, 2000

We consider a model for gravity in which the linear part of the four-derivative terms ò

R

_mn

R

^mn

d

⁴

x

and ò

R

²

d

⁴

x

are included into the Fierz-Pauli gravitational action. Unitarity is discussed at the tree-level. The issue of the gravitational deflection of a light ray is also considered.

I Introduction

Einstein's field theory accounts very well for all known macroscopic gravitational phenomena. The theory is defined by action

where k² = 32 pG , G being Newton's constant, is the Einstein's constant. The possibility of a cosmological constant, which experimentally must be very small, was ignored.

However, as a quantum theory it is less satisfactory, since pure gravity has an S matrix which, despite being finite at one-loop level [1], diverges at the two-loop order [2].

Thus, it is rather natural for the quantum field theorist to view (1) as a long-distance approximation to some action which exhibits better ultraviolet behavior, and defines a meaningful quantum theory. Now, as is well known, (1) is not the most general action allowed for the symmetries (general covariance) of the theory. The general action is given by [3]

where a¢, b¢, g¢, etc., are suitable parameters. The so called higher derivative gravity, in turn, is defined by the action

where a and b are dimensionless coupling parameters. Deser and van Nieuwenhuizen [4] argued that such theory would be renormalizable but contain ghosts due to the k^-4 propagators. On the other hand, Antoniadis and Tomboulis [5] pointed out that the presence of a massive spin-2 ghost in the bare propagator of quadratic gravity is inconclusive, since this excitation is unstable. Stelle [6] proved rigorously the renormalizability of the action (2).

Actually, not every higher derivative theory necessarily has ghosts or tachyons [7]. This result led us to consider a model for gravity which contains, in addition to the linear part of the four-derivatives terms òR_mnR^mnd⁴x and òR²d⁴x, the Fierz-Pauli gravitational action. This model, however, as far as the tree-level unitarity is concerned, fell far short of our expectations. But on the other hand, it has its virtues as well which we think make its study worthwhile. Indeed, it agrees asymptotically with Newton's law - besides it predicts an acceptable value for the gravitational deflection. It also allows us to find the effective coupling constant for Fierz-Pauli gravity.

Having checked that the linear part of the four-derivative term òd⁴x is the Achille's heel of Fierz-Pauli gravity with higher derivatives, we considered afterward a model wherein only the linear part of the four-derivative term òR²d⁴x is included into the Fierz-Pauli gravitational action. The resulting theory is unitary at the tree level and in addition gives, in the limit of tiny masses, a value of 1.31 arcsec for the deflection of a light beam passing near to the Sun.

In Sec. II we examine in detail the question of the tree-level unitarity of quadratic gravity. Our aim in so doing was in first place to provide a prescription which allowed us to discuss with facility the tree-level unitarity of whatever theory of gravitation with higher derivatives we wished; and secondly, to present a rigorous treatment of the issue related to the unitarity of higher derivative gravity at the tree level, filling in this way a gap in the literature on the subject. In Sec. III we discuss Fierz-Pauli gravity with higher derivatives. "Fierz-Pauli + R² gravity" is analyzed in Sec. IV.

In our notation the signature is (+ - - -). The curvature tensor is defined by R^a_bgd = - ¶_d + ..., the Ricci tensor by R_mn = , and the curvature scalar by R = g^mnR_mn, where g_mn is the metric tensor. Natural units are used throughout.

II Tree-level unitarity and bending of light in the context of higher derivative gravity

In the weak field approximation, i. e., g_mn = h_mn + kh_mn, where h_mn = diag (+1, -1, -1, -1), the higher derivative gravity Lagrangian reduces to

where A^mº h^mn_{, n} , f º h , F_mnº A_{m, n} - A_{n, m}, b º , c º . Indices are lowered (raised) using h_mn (h^mn).

In order to verify whether ghosts and tachyons are absent in (3), we require that the propagator has only first order poles at k² - M² = 0 with real masses M (no tachyons) and with positive residues (no ghosts) [8]. Let us then determine the propagator for higher derivative gravity. To do that, we add to (3) the gauge-fixing Lagrangian

The resulting Lagrangian,

can be cast into the bilinear form

where the operator is given by [9]

whereupon

and

with

P¹, P², P⁰, ⁰ and ⁰ are the Barnes-Rivers operators [10] and k_m is the momentum of the graviton exchanged.

Then the propagator in momentum space is

The choice

= 0, gives the propagator

with

Note that all parts of the propagator (5) behave like k^{- 4}. This choice corresponds to the Julve-Tonin gauge [11].

We are now ready to probe the tree-level unitarity of higher derivative gravity. To accomplish this we couple the propagator (5) to external conserved currents, T^mn, compatible with the symmetries of the theory and then we examine the residue of the current-current amplitude at the poles. Therefore, the transition amplitude in momentum space can be written as

where g is the effective coupling constant of the theory. Now, taking into account that k_mT^mn = 0, we come to the conclusion that only the spin-projectors P² and P⁰ will give a non null contribution to the current-current amplitude. As a consequence,

Thus, we have two poles for both the spin-2 sector, i. e.,

and the spin-0 sector, namely,

In summary, the theory of quadratic gravity yields a massless and two massive excitations. Absence of tachyons requires that b < 0 and 3a + b > 0.

From (6) we promptly obtain

where T º h_mnT^mn = T^m_m.

Now we expand the sources in a suitable basis. The set of independent vectors in momentum space,

where ₁ and ₂ are mutually orthogonal unit vectors which are also orthogonal to k, serves our purpose. Accordingly, the symmetric current tensor T^mn (k) can be written as

The current conservation, k_mT^mn = 0, gives the following constraints for the coefficients a, b, d, eⁱ and fⁱ

If we saturate the indices of T^mn with momenta k_m, we obtain the equation k_mk_nT^mn = 0 , which yields a consistency relation for the coeficients a, b and d

From (7), (8), (9) and (10) we conclude that the residue of A at the pole k² = 0 is

So, the necessary condition for tree-level unitarity, i. e., Res A > 0 at the pole, is ensured as far as the pole k² = 0 is concerned.

Similarly, we find the residue at the pole k² = . The result is

where use has been made of (8), (9), (10) and (11). This expression can also be written as

Now, assuming as usual that T ³ 0, we get that cⁱⁱ£ 0, which implies that Res A |_k² = < 0. So, we have a massive spin-2 ghost in the bare propagator of higher derivative gravity. This ghost is nontachyonic since we have assumed that b < 0 ( > 0). In short, quadratic gravity is nonunitary.

Of course, Res A |_k² = > 0. Thus, the scalar massive particle is a physical one. Note that we have supposed that 3a + b > 0 ( > 0).

Let us take for granted, for a while, that the massive spin-2 particle of negative residue, i. e., the ghost, is unstable [6]. Now, according to Feynman, The test of all knowledge is experiment [12]. In this vein, we should expect that higher derivative gravity, viewed as a classical theory, passed the tests suggested by Einstein for general relativity. Since we are dealing with the linearized version of higher derivative gravity, we will concentrate our attention only on the issue of the gravitational deflection of a light ray. Let us then consider the interaction between a fixed source, like the Sun, and a light ray. The associated energy-momentum tensors will be designated respectively as T^mn and F^mn. The current-current amplitude for this process is given by

Taking into account that the energy-momentum tensor for light (electromagnetic radiation) is traceless, while T^mn = d^m₀ⁿ₀T⁰⁰ for a static source, we get

Note that the harmless massive scalar mode gives no contribution at all to the gravitational deflection. Incidentally, it does not contribute either to the light deflection in the framework of R + R² gravity [13, 14]. From (13) we see that the value of the deflection angle, q_Q.G., at the Sun's limb predicted by quadratic gravity is always smaller than that predicted by general relativity (q_E = 1.75¢¢). Fig. 1 shows a qualitative plot of deflection versus m₁ for rays passing by the Sun. In the measurement of the solar gravitational deflection of radio waves Robertson and al. [15] found that = 1.0001 ± 0.0001 for the deflection at the solar limb, where q_theor is the deflection predicted by general relativity. So, q_Q.G. < q_measured.

Figure 1
- Deflection vs. m₁.

III Fierz-Pauli higher derivative gravity

To arrive at the Lagrangian for Fierz-Pauli higher derivative gravity we add the linear part of the Lagrangian containing the four-derivative terms R² and , namely,

where b º b, c º , being the "Einstein's constant" for Fierz-Pauli gravity [16], to the Fierz-Pauli Lagrangian, i. e.,

In momentum space the resulting Lagrangian can be written as

Since this theory is not gauge invariant owing to the Proca-like mass term, we do not need to introduce any gauge fixing term into (14) in order to find the propagator. As a result, all we have to do in this case is to invert the operator

Using the algorithm presented in Ref. [9] for computing the propagator for higher derivative gravity theories, we promply obtain

If we take b = c = 0 in (15) we recover the propagator concerning Fierz-Pauli gravity [16], namely,

where we have omitted the terms proportional to the graviton momentum.

Our task now is to find out whether or not Fierz-Pauli higher derivative gravity gives an acceptable Newtonian limit. To succeed in doing this we compute the effective nonrelativistic potential for the interaction of two identical massive bosons of zero spin via a graviton exchange. The expression for the potential is

whereupon

_N.R is the nonrelativistic limit of the Feynman amplitude for the process s + s ® s + s, where s stands for a spinless boson of mass M. The corresponding Feynman diagram is shown in Fig. 2.

Figure 2
- Lowest order contribution to the raction s + s ® s + s, where s stands fot a spinless massive boson.

The Lagrangian for the interaction of gravity with a free, massive scalar field

, is

From the previous expression the Feynman rule for the elementary vertex may readily be deduced. It is shown in Fig. 3.

Figure 3
-The relevant Feynman rule for boson-boson interation.

Accordingly, the invariant amplitude for the process shown in Fig.2 is

whereupon

where º - = - . Absence of tachyons requires that b < 0 and > 2 m².

In the nonrelativistic limit this expression reduces to

Substituting (17) into (16) and performing the integration we obtain the expression for the nonrelativistic potential

from which it follows immediately the expression for "Fierz-Pauli generalized potential"

It is easy to see that (18) tends to the Fierz-Pauli potential, i. e.,

as ® ¥. Comparison of this result, in the limit of an extremely small mass, with the Newtownian potential V_N(r) = - , shows that 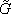= G. As a consequence, ²/g² = 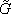/G = 3/4 , where is the effective coupling constant for Fierz-Pauli theory.

A cursory look at (18) allows us to conclude that at the origin that expression tends to the finite value

M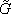 l(M₂ - M₁) / 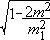. It is interesting to note that only in the absence of tachyons (both positive and negative energy) in the dynamical field does Fierz-Pauli higher derivative gravity agree asymptotically with Newton's Law.

Let us now examine the question of unitarity (at the tree level) of Fierz-Pauli higher derivative theory. To begin with we analyze the poles to get information on the physicality of the masses. As we have already mentioned, tachyons are excluded from the spectrum whenever b < 0 and > 2 m². It is trivial to see in this case that we have two massive spin-two particles, one with square mass and another with square mass . One can verify promptly, that the residue of the transition amplitude at the pole k² = is negative, which implies that Fierz-Pauli higher derivative gravity is nonunitary. The residue of the transitions amplitude at the pole k² = , in turn, is positive. Thereby, the particle of mass M₂ is a physical one, while that of mass M₁ is a ghost.

The transition amplitude for the interaction between a static source and a light beam is given, in turn, by (see Sec. II)

For m² extremely small, this expression tells us that 0 < q_F.P.H.G. < 1.31¢¢, where q_F.P.H.G. is the deflection predicted by Fierz-Pauli higher derivative gravity. As a consequence, in this limit q_F.P.H.G. < q_measured.

IV Final remarks

Despite its interesting properties, Fierz-Pauli higher derivative gravity did not come up to our expectations as far as the issue of unitarity is concerned. However, it is easy to see that the massive spin-2 ghost that appears in the bare propagator of Fierz-Pauli higher derivative gravity is entirely due to the linear part of the four-derivative term ò d⁴x. So, it is worthwhile to consider a model for gravity in which only the linear part of the four-derivative term òR²d⁴x is included into the Fierz-Pauli gravitational action. For the sake of simplicity, let us call this theory "Fierz-Pauli + R² gravity". The corresponding Lagrangian is given by

which, in momentum space, reduces to

Thus, the propagator in momentum space is

Of course, the inclusion of the linear part of the four-derivative term òR²d⁴x into the Fierz-Pauli gravitational action does not improve the ultraviolet behavior of the usual Fierz-Pauli theory.

It is easy to see that Fierz-Pauli + R² gravity is unitary at the tree-level. On the other hand, the transition amplitude for the interaction between a static source and a light beam is given by (see Sec. II)

In the limit of an extremely small mass, Fierz-Pauli + R² gravity gives a value for the bending of a light ray passing close to the Sun which is 34 of that predicted by general relativity. So,

Note that the prediction of both Fierz-Pauli + R² gravity and Fierz-Pauli gravity for the solar gravitational deflection are one and the same (as expected).

Acknowledgment

E. de Rey Neto is very grateful to Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) for financial support.

References

[1] G. 't Hooft and M. Veltman, Ann. Inst. Henri Poincaré 20, 69 (1974).

[2] Marc H. Goroff and Augusto Sagnotti, Phys. Lett. B 160, 81, (1985).

[3] John F. Douglas, Phys. Rev. Lett. 72, 2996 (1994).

[4] S. Deser and P. van Nieuwenhuizen, Phys. Rev. D 10, 401 (1974).

[5] I. Antoniadis and E. T. Tomboulis, Phys Rev. D 33, 2756 (1986).

[6] K. S. Stelle, Phys. Rev. D 16, 953 (1977).

[7] E. Sezgin and P. van Nieuwenhuizen, Phys. Rev. D 21, 3269 (1980).

[8] P. van Nieuwenhuizen, N. Phys. B 60, 478 (1973); F. C. P. Nunes and G. O. Pires, Phys. Lett. B 301, 339 (1993); C. Pinheiro, G. O. Pires and F. A. B. Rabelo de Carvalho, Braz. J. Phys. 27, 14 (1997).

[9] A. Accioly, S. Ragusa, H. Mukai and E. de Rey Neto, Int. J. Theor. Phys. 39, 1601 (2000).

[10] R. J. Rivers, Nuovo Cimento 34, 387 (1964).

[11] J. Julve and M. Tonin, Nuovo Cimento B 46, 137 (1978).

[12] R. P. Feynman, R. B. Leighton and M. Sands, The Feynman Lectures on Physics, vol. I (Addison-Wesley, 1966).

[13] A. Accioly, A. D. Azeredo, E. C. de Rey Neto and H. Mukai, Braz. J. Phys. 28, 496 (1998).

[14] A. Accioly, S. Ragusa, E. C. de Rey Neto and H. Mukai, Nuovo Cimento B (Note Brevi) 114, 595 (1999).

[15] D.S. Robertson, W. E. Carter and W. H. Dillinger, Nature 349, 768 (1991).

[16] P. van Nieuwenhuizen, Phys. Rev. D 7, 2300 (1973).

[17] H. van Dam and M. Veltman, N. Phys. B 22, 397 (1970).

Publication Dates

• Publication in this collection
  11 Jan 2002
• Date of issue
  2000

History

• Received
  20 Dec 1999
• Reviewed
  31 May 2000