Relativistic equation of state with short range correlations

NUCLEON STRUCTURE AND INTERACTIONS

Relativistic equation of state with short range correlations

P. K. Panda^I; D. P. Menezes^I; C. Providência^II; J. da Providência^II

^IDepartamento de Física-CFM, Universidade Federal de Santa Catarina, CP. 476, 88040-900 Florianópolis-SC, Brazil

^IICentro de Física Teórica - Dep. de Física, Universidade de Coimbra, P-3004 - 516 Coimbra, Portugal

ABSTRACT

Short range correlations are introduced using unitary correlation method in a relativistic approach to the equation of state of the infinite nuclear matter in the framework of the Hartree-Fock approximation. The effect of the correlations in the ground state properties of the nuclear matter is studied.

In this paper we introduce short range correlations in a relativistic approach to the description of nuclear matter for the first time. Although there are several procedures which may be used to introduce short range correlations into the model wave function, we work with the unitary operator method as proposed by Villars [1]. There are several advantages in using an unitary model operator. In particular, one automatically guarantees that the correlated state is normalized. The general idea of introducing short range correlations in systems with short range interactions exists for a long time [2, 3] but has not been pursued for the relativistic case.

Nonrelativistic calculations based on realistic NN potentials predict equilibrium points that are not able to describe simultaneously the correct binding energy and saturation density; either the saturation density is correct but the binding energy is too small, or the correct binding energy is obtained at a too high density [4]. In order to solve this problem a repulsive potential or density-dependent repulsive mechanism [5] is included. Due to Lorentz covariance and self-consistency, relativistic mean field theories [6] include automatically contributions which are equivalent to n-body repulsive potentials in non-relativistic approaches.

In non-relativistic models the interaction arises from the interplay between a long range attraction and a very strong short range repulsion and it is indispensable to take short range correlations into account. In relativistic mean field models, the parameters are phenomenological, fitted to the saturation properties of nuclear matter. Short range correlation effects may be included to some extent in the model parameters. However, we want to study the consequences of taking these effects into account explicitly [7].

We start with the effective Hamiltonian as

with

where

and are the Dirac-matrices. In the above, y is the nucleon field interacting through the scalar and vector potentials. The equal time quantization condition for the nucleons is given by

where a and b refer to the spin indices. The field expansion for the nucleons y at time t=0 is given by [8]

where U_r and V_r are

For free spinor fields, we have cosc() = M/e(), sinc() = |/e() with e() = . However, we will deal with interacting fields so that we take the ansatz cosc() = M*()/e*(), sinc() = |*|/e*(), with e*() = , where * and M*() are the effective momentum and effective mass, respectively. The equal time anti-commutation conditions are

The vacuum | 0ñ is defined through | 0ñ = | 0ñ = 0; one-particle states are written |, rñ = | 0ñ; two-particle and three-particle uncorrelated states are written, respectively as |, r; ¢, r¢ñ = | 0ñ, and |, r; ¢, r¢; ¢¢, r¢¢ñ =

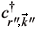| 0ñ, and so on.

We now introduce the short range correlation through an unitary operator method. The correlated wave function[9] is |Yñ = e^iW|Fñ where |Fñ is a Slater determinant and W is, in general, a n-body Hermitian operator, splitting into a 2-body part, a 3-body part, etc.. The expectation value of H is

In the present calculation, we only take into account two-body correlations. Let us denote the two-body correlated wave function by

where f₁₂ is the short range correlation factor, the so-called Jastrow factor [10]. For simplicity, we consider f₁₂ = f(₁₂), ₁₂ = ₁ - ₂, and f(r) = 1 - (a + br) e^-gr where a, b and g are parameters. The important effect of the short range correlations is the replacement, in the expression for the ground-state energy, of the interaction matrix element á, r; ¢, r¢ |V₁₂| , r; ¢, r¢ñ by á|V₁₂ + t₁ + t₂|ñ - á, r; ¢, r¢ |t₁ + t₂| , r; ¢, r¢ñ, where t_i is the kinetic energy operator of particle i. As argued by Moszkowski [11] and Bethe [12], it is expected that the true ground-state wave function of the nucleus containing correlations coincide with the independent particle, or Hartree-Fock wave function, for interparticle distances r > r_heal, where r_heal » 1 fm is the so-called "healing distance". This behavior is a consequence of the constraints imposed by the Pauli Principle. A natural consequence of having the correlations introduced by an unitary operator is the occurrence of a normalization constraint on f(r),

The correlated ground state energy becomes

where A_i, B_i, C_i , I and J are exchange integrals. In the above equation for the energy density, the first term results from the kinetic contribution, the second and third terms come respectively from the s and w direct contributions from the potential energy with correlations, the fourth from the exchange correlation contribution from the kinetic energy, and the last one from the s + w exchange contributions from the potential energy with correlations. The direct correlation contribution is zero due to (10). The angular integrals are given by A_i(k, k¢) = B_i(k, k¢) = 2p /4p d cosq (k, k¢, cosq), C_i(k, k¢) = 2p /4p cosq d cosq (k, k¢, cosq), I(k, k¢) = 2p d cosq (k, k¢, cosq), and J(k, k¢) = 2p cosq d cosq (k, k¢, cosq), where

The baryon density and the scalar density are

The couplings g_s, g_w, the meson masses, m_s and m_w and also three more parameters from the short range correlation function, a, b and g have to be fixed. The couplings are chosen so as to satisfy the ground state properties of the nuclear matter. We choose m_s = 550 MeV and take m_w = 783 MeV. The normalization condition (10) determines b. We fix a by minimizing the energy. For the parameter g we consider a function which increases linearly with the Fermi momentum, of the form g = a₁ + a₂k_F/k_F0 where a₁ and a₂ are free parameters. This is consistent with the idea that the healing distance decreases as k_F increases.

The correlation function f(r) is plotted in Fig. 1 as a function of the relative distance. The inclusion of correlations introduces an extra node in the ground-state wave-function contrary to what generally happens in non-relativistic calculations with a hard core. In this case the wave function has a wound. The quantities cos(c(k)/2) and sin(c(k)/2) are plotted in Fig. 2. They show how the interaction and correlations make the wave-function deviate from the free wave-function, represented by a dotted line. The correlated angle c(k) lies between the Hartree-Fock(HF) and the free wavefunction angles. As a consequence, we will see that the correlated effective mass will not decrease so fast with density as the HF effective mass.

In table I, we have tabulated the parameters used in our calculation together with the compressibility K, the relative effective mass M*/M, the kinetic energy /r_B - M, the direct and exchange parts of the potential energy (_d/r_B and _e/r_B respectively) with correlation and the correlation contribution to the kinetic energy ^C/r_B, all calculated at the saturation point. Notice that a HF calculation produces an EOS which is stiffer than the one obtained at the Hartree level. However, the inclusion of correlations gives a larger effective mass than both Hartree and HF calculations and a softer EOS. In fact, the contribution of direct and exchange correlation terms are of the same order of magnitude of the other terms in the energy per particle. Hence, they cannot be disregarded.

We have computed the binding energies as function of the density for the Hartree, HF and HF+Corr and compared with the quark-meson-coupling model (QMC) [13] and a non-linear Walecka model NL3 [14], as can be seen from Fig. 3. The inclusion of correlations make the equation of state (EOS) softer than Hartree or HF calculations. NL3 and QMC also provide softer EOS around nuclear matter saturation density but around two times saturation density, the EOS with correlations is softer than NL3. In Fig. 4 we plot the effective mass as a function of density. If correlations are included the effective mass does not decrease so fast with the increase of density as in a Hartree or, even worse, HF calculation. This explains the softer behavior of the EOS with correlations.

We conclude referring that, although correlation effects in the Hartree and HF calculations may be taken partially into account by a correct choice of the coupling constants, the explicit introduction of correlations has other effects such as softening the EOS.

ACKNOWLEDGMENTS

This work was partially supported by CNPq (Brazil), CAPES (Brazil)/GRICES (Portugal) under project 100/03, FEDER and FCT (Portugal) under the projects POCTI/FP/FNU/50326/2003, POCTI/FIS/451/94 and POCTI/FIS/35304/2000.

REFERENCES

[1] F. Villars, "Proceedings of the International School of Physics, 'Enrico Fermi'-Course 23, (1961)." Academic Press, New York, 1963; J.S. Bell, "Lectures on the Many-Body Problem, First Bergen International School of Physics." Benjamin, New York, (1962); F. Coester and H. Kümmel, Nucl. Phys. 17 477 (1960).

[2] J. da Providencia and C. M. Shakin, Ann. Phys.(NY) 30, 95 (1964).

[3] H. Feldmeier, T. Neff, R. Roth, and J. Schnack, Nucl. Phys. A632, 61 (1998); T. Neff and H. Feldmeier, Nucl. Phys. 713 311 (2003).

[4] F. Coester, S. Cohen, B.D. Day, and C.M. Vincent, Phys. Rev. C1, 769 (1970); R. Brockmann and R. Machleidt, Phys. Rev. C42, 1965 (1990).

[5] R. B. Wiringa, V. Fiks, and A. Fabrocini, Phys. Rev. C38, 1010 (1988); W. Zuo, A. Lejeune, U. Lombardo, and J.-F. Mathiot, Nucl. Phys. A706, 418 (2002).

[6] B. D. Serot, J. D. Walecka, Int. J. Mod. Phys. E 6, 515 (1997).

[7] P. K. Panda, D.P. Menezes, C. Providência, and J. da Providência, Phys. Rev. C71, 015801 (2005).

[8] A. Mishra, P.K. Panda, S. Schramm, J. Reinhardt, and W. Greiner, Phys. Rev. C56, 1380 (1997).

[9] J. da Providencia and C. M. Shakin, Phys. Rev C4, 1560 (1971); C. M. Shakin, Phys. Rev. C 4, 684 (1971).

[10] R. Jastrow, Phys. Rev. 98, 1479 (1955).

[11] S. A. Moszkowski and B. L. Scott, Ann. Phys. (N.Y.), 11, 65 (1960).

[12] H. Bethe, Ann. Rev. Nucl. Sci. 21, 93 (1971).

[13] P. A. M. Guichon, Phys. Lett. B 200, 235 (1988). K. Saito and A. W. Thomas, Phys. Lett. B 327, 9 (1994); P.K. Panda, A. Mishra, J. M. Eisenberg, and W. Greiner, Phys. Rev. C 56, 3134 (1997).

[14] G. A. Lalazissis, J. König, and P. Ring, Phys. Rev. C 55, 540 (1997).

Received on 9 June, 2005

Publication Dates

• Publication in this collection
  07 Nov 2005
• Date of issue
  Sept 2005

History

• Received
  09 June 2005