Conservation laws in a metric nonsymmetric theory of gravitation

Conservation laws in a metric nonsymmetric theory of gravitation

S. Ragusa

Instituto de Física de São Carlos, Universidade de São Paulo, C.P. 369, 13560-970 São Carlos, SP, Brazil, Email address: [e-mail]

ABSTRACT

The conservation laws associated with a previously studied metric nonsymmetric theory of gravitation are established and their physical significance is discussed. Conservation laws are obtained for the generalized energy and momentum. Some applications of the results are made for a spherically symmetric fluid with a view to future study of stelar equilibrium.

I. INTRODUCTION

In previous works [1] a generalized theory of gravitation based on a nonsymmetric metric tensor g_ab have been studied. After establishing the field equations in [1-I] their solution for a point source mass was obtained in [1-II], together with its implications for the motion of test particles and light. The theory was shown to be consistent with the four classical solar tests of general relativity (GR). Next, in [1-III], the electromagnetic field was included into the theory and the solution for a point charge was obtained. In a more recent paper, ]1-IV], it was shown that the theory is definitely free of ghost-negative radiative modes even when expanded around a Riemannian GR background space.

The sources of the field are the energy-momentum-stress tensor T_ab and the fermionic current density S^a. For a macroscopic system this current is taken to be S^a = fnu^a, where f is the coupling to the geometry, u^a is the velocity and n is the rest number density found, for instance, in the description of the interior of stars (electrons, protons and neutrons).

It is the aim of this paper to establish the conservation laws for the generalized energy and momentum and discuss their physical significance. Some of the results are applied to a perfect fluid with a view to future application to the study of stelar equilibrium.

The paper is organized as follows. We present the field equations in Sec. II. In Sec. III the Variational Principle is discussed and the conservation of energy and momentum are established. In Sec. IV we will deduce an equation expressing the total energy of a system as an integral over the sources of the field. In Sec. V we make some applications to a static spherically symmetric perfect fluid. In Sec. VI we draw our conclusions and highlight future works.

II. THE FIELD EQUATIONS

The field equations of the theory are [1-1]

and

We use the notation a_(ab) = (a_ab + a_ba)/2 and a_[ab] = (a_ab – a_ba)/2 for the symmetric and antisymmetric parts of a_ab and the notation a_[ab,g] = a_[ab],g + a_[ga],b + a_[bg],a for the curl of a_[ab]. In the first equation

symmetric because the second term is (see (2.12) below) and containing only the symmetric part of the connection, is the analogue of the Ricci tensor. L is the cosmological constant and we have used the notation

In (2.3) and (2.4) the notation X = X with g=det(g_ab) is being used and g^ab is the inverse of g_ab as defined by

Equation (2.2), came as the result of

where G_a = is a vector involving contractions of the antisymmetric part of the connection. From (2.4) we have ¶_aS^a = 0, the equation of continuity for the fermionic current, saying that

is a constant. This is the fermionic charge of the system.

Equation (2.3) can be solved for the symmetric part of the connection (1-I) giving ,

where s_ab, symmetric and with determinant s, is the inverse of g^(ab) as defined by

In deriving Eq. (2.10) from (2.3) we come across the relation

which can be re-obtained from (2.3). One then sees that the second term on the right of (2.5) is in fact symmetric.

The total Lagrangian density we ended up with in [1-I] is

where L is the field Lagrangian,

this being Eq. (1-I:5.13) here without the unnecessary factor 2/3 and with the replacement of D_a by G_a. L_M is the interaction matter part, modeled after GR, containing here the generalized nonsymmetric energy-momentum-stress tensor T_ab and the fermionic current S^a, as given by

where k = 8pG as usual. Using dg^ab = dg^ab – g^abg_mndg^mn/2 we can also write

Together with the down-indices T_ab, defined in (2.15),

we will be working with the upper-indices stress tensor T^mn defined by the variation with respect to g_mn,

This second stress is related to the first one [1-I] by

which follows from the relation dg_mn/dg^ab = –g_ang_mb resulting from the variation of (2.7). It should be kept in mind that (2.19) does not imply a rule for lowering indices because this operation is not defined for a nonsymmetric metric. A better name for the upper-indices stress would probably be Z^mn but we shall use the same T for both tensors. Notice that the inverse relation is T^mn = g^mbg^anT_ab and that both tensors have the same trace g_mnT^mn = g^abT_ab. Also, even for a symmetric upper-indices stress as is the case for a pressureless fluid with the dust-like form T^mn = ru^µuⁿ, r being the matter rest density, T_ab will have a symmetric and a nonsymmetric part as well.

III. THE VARIATIONAL PRINCIPLE

We will now derive the field equations and the differential form of the conservation laws following the standard procedure in GR [3]. Following the same strategy as in GR we take (2.3) for grant and use it to get rid of the second-order derivatives of the metric which are present in the term g^(ab)U_ab of the free Lagrangian (2.14). Upon contraction of (2.5) with g^(ab) and making use of (2.3) and

that comes from it, we obtain

where

and

Therefore, the free Lagrangian can be written as

where

The variation of the action

under variations of the field variables will receive no contribution of the divergence term because that term leads to an integral of M^s over the surface S enclosing the volume W , where the variations dg^ab and dg^ab,_s are required to vanish. Therefore

As L₁ does not depend on g^ab,_s and L' not on G_a,b we have

From the requirement dI = 0 for dg^ab and dG_a arbitrary in W but vanishing on S it follows the field equations (2.1), (2.2) and (2.4), the first two coming from

To obtain this equation one makes use of the two relations

and

the details of which we give in ^{Appendix A}. This gives

if we remember that is symmetric from (2.12), which comes from (2.3) that was taken for grant from the very beginning.

We consider the action corresponding to L'

which remains invariant under linear coordinate transformations because L' transforms as a scalar density under such a kind of transformations. We consider infinitesimal linear transformation of the form

with x^a=constant or x^a _,s=constant Thence the reduced actions calculated in the two frames, I' in (3.14) and

are equal, = I'. They are also equal when the x^a(x) are arbitrary but vanish on the boundary S of W because according to (3.1) L' differ from a true Lagrangian by a divergence.

We calculate now the difference between these actions. Expressing the volume d⁴x in terms of d⁴ using (3.15) to write

followed by '() = '(x) + ex^sL' ,_s, the difference between the actions is given by

where

This is the variation of L', given by

using (3.13). With the help of (3.15) and (3.17) we have for the variation dg^ab(x) = ^ab(x) – g^ab(x),

Taking this and the previous relation into (3.18) and integrating by parts the U_ab term yields

Under variations which vanish on the border S the second integral vanishes, so that for arbitrary x^a

With this identity the right-hand side of (3.22) is reduced to its second integral. Next, for x^a = arbitrary constants, we find the second identity,

Finally we consider the vanishing condition x^a,_s = arbitrary constants, to obtain the last identity which can be derived from L',

where use has been made of the a,b symmetry of .

After substituting the value of U_ab from (3.10) a little calculation, with details in ^{Appendix B}, yields the following three equations. From (3.23) we have the matter-response equation

where

and where for short

Next the second identity leads to

where

The third identity in (3.25) allows us to write the quantity inside the parenthesis of (3.29) as a divergence. Making use of (3.12), (2.10), (2.12) and (3.1) a straightforward calculation, the details of which are given in ^{Appendix B}, leads to the following final result

where the superpotential, as is called the corresponding quantity in GR, is given by

where s_la is the inverse of g^(la) according to Eq. (2.8).

It should be pointed out that the matter-response equation (3.26) can also be derived [1-I] directly from the matter Lagrangian (2.16).

IV. CONSERVATION OF ENERGY AND MOMENTUM

We will be applying our considerations to a limited system whose changes can produce no changes in the gravitational field on and out of a sufficiently distant boundary surface enclosing the system. Such a system will be referred to as an isolated system. If we integrate (3.29) and call S the surface surrounding the matter distribution located around the origin, we obtain

We will show that the surface integral vanishes,

leading to the four conservation of energy and momentum within the boundary taken

In the case of the energy (4.2) involves the component t₀ⁱ of the pseudotensor density given in (3.30),

in accordance with the fact that the gravitational field is supposed not to change in time at the boundary S. As it is far away we have there weak field, being then enough the solution in the Minkowskian flat space approximation. In this situation (2.4) and (2.8) become, except for the last term of this last one, similar to the Maxwell equations with the flat space values h_[ab] of g_[ab] and of G_a playing the role of the field strength and potential. Then we infer that to lowest order this fields at large distances r of the origin around which the material system is located behaves as

and

This is in fact the case as it is discussed in detail in ^{Appendix C}. This means that at infinity t₀ⁱ goes as r^–5 and higher so the surface integral in (4.2) for a = 0 indeed vanishes. Therefore, the energy P₀ is in fact constant.

For the momentum the appropriated component is

with the cosmological constant now present. This is similar to the situation present in the work of Tolman [4] in his study of the conservation laws in GR when L is present. We follow then his considerations. We need the flat space solution of the gravitational field (2.1) involving L. As discussed in ^{Appendix D} the solution is the Schwazschild metric solution of GR with the well known Lr² term together with the GM/r term in the components g₀₀ and g_ii (no sum). Now, as remarked by Tolman [4], in the case of the energy there was no restriction on how far the boundary was to be taken, it could be the whole universe, but not so for the momentum because now L is present. To have the vanishing of the surface integral assured in this case we have to be at distances large enough so that terms of order (GM/r)² can be neglected, and at the same time small enough that the cosmological term Lr² can be neglected too. The systems at hand are then those which are small compared to the total dimensions of the universe even though, of course, very large compared with ordinary terrestrial dimensions. In this situation the solution for the metric is

Thence, as goes as r^–2 we see from (3.12), (4.5) and (4.6) that t_jⁱ is of order r^–4, meaning that the surface integral vanishes. Therefore, P_i is also constant.

We can calculate these constants by integrating (3.31) recalling the time independence at a far away surface S enclosing the system,

For a = 0 the asymPTOTIC VALUE OF THE SUPERPOTENTIAL IS EASILY FOUND to be A₀⁰ⁱ = 2GMxⁱr^–3. Therefore,

A similar calculation for the space components leads to the result

as we should expect from the fact that the asymptotic metric is stationary.

V. THE ENERGY AS AN INTEGRAL OVER THE MATERIAL SOURCE

When the field is stationary we can express the total energy of the field as an integral over the material sources, again following the same steps as in GR [4], by neglecting also here the contribution of the cosmological constant. As the field is time-independent (3.29) reduces to

with the help of which we can write

If we integrate this expression in all space the integral of the right-hand side can be written as a surface integral, which vanishes This is so because, as we are outside the localized material sources, T_a^j vanishes and far away t_a^j ~ r^–5 for a = 0 and ~ r^–4 for a = i. Thence,

From (3.30) we have, for a stationary field,

Consider now the trace of the same equation,

Making use of (2.3) and (3.12) we easily find

recalling Eq. (3.4). Thence,

With the help of Eq. (5.5) we then find

From (4.3) and (5.3) we can write

and using (5.8),

The last term inside the brackets can be written as g^[0i]G_0,i = (g^[0i]G₀)_,i –g^[0i]_,iG₀. The integral of the first term can be written as a surface integral at infinity which vanishes con account of (4.5) and (4.6). Then by using the field equation Eq. (2.4) we finally obtain

where the abbreviation in (3.28) should be kept in mind. This expresses the total energy of a stationary system as an integral over the sources of the field.

VI. APPLICATIONS TO A SPHERICAL SYMMETRIC PERFECT FLUID

The matter stress tensor for a perfect fluid with energy density r, pressure p and velocity u^µ has the same form of the GR expression

with the proviso that now the metric is nonsymmetric. This was obtained before [5] in the context of a different nonsymmetric theory of gravitation but it is valid in our case too because only the field part of the Lagrangians are different, ours being given in (2.14), and they do not interfere in the process of obtaining T^mn: Lagrange multipliers enforces the normalization of u^a, conservation of rest mass and of the particle number and of entropy.

We consider a spherically symmetric distribution contained in a radius R and ask for the corresponding form of the matter-response equation (3.26).

The static and spherically symmetric metric tensor in polar coordinates xº = t, x¹ = r, x² = Q and x³ = F is of the form

and all other components equal to zero. The non-zero components of the inverse matrix are then

In this situation a straightforward calculation shows that the mass-response equation in a commoving frame, where uⁱ = 0 and uº = (g₀₀)^–1/2, acquires the simple form ( ' = d/dr)

As a second application we look now for the expression of the rest energy of the sphere, P₀ = M, from (5.11).

Taking (6.1) into (3.28) we obtain

Thence, in commoving coordinates, T₀ ⁰ = r and T_iⁱ = –3p. Therefore, (5.10) gives

Equations (6.4) and this one are of use when studying the interior problem for a bounded spherical perfect fluid system.

VII. CONCLUSIONS

Giving sequence to a program of study on a theory of gravitation based on a nonsymmetric metric [1], we have studied here the conservation laws associated to the theory. As in GR the invariance of the Lagrangian under suitable coordinate transformation leads to identities which when supplemented by the field equations lead to physical conservation laws. Here we have established the conservation laws for the generalized energy and momentum. The energy of a stationary field could be written as an integral over its sources, which are the matter stress tensor and the fermionic current density. Some applications for a spherically symmetric perfect fluid have been written down with a view to a study of stars.

As a topic for future work it would be interesting to analyze the interior problem for a bounded spherically symmetric perfect fluid system as a model for a star. This could be followed by a study of what the modifications of the predictions of GR are for stelar equilibrium and collapse. This particularly by the fact that, together with the stress tensor, the matter current is also a source of gravitation.

References

[1] S. Ragusa, S. Phys. Rev. D 56, 864 (1997). D in this paper is now named G.; Gen. Relat. Gravit. 31, 275 (1999). In the first term inside the first brackets of Eq. (23) the numerator should be a' instead of g'. The exponent of r in the expression in the middle of the second line below Eq. (33) should be 2 instead of 3. S. Ragusa and D. Bosquetti, Braz. J. Phys. 30, 569 (2000). S. Ragusa and Lucas C. Céleri, Braz. J. Phys. 33, 821 (2003). These papers will be referred to as I-IV, respectively.

[2] S. Ragusa, Phys. Rev. 62, 024026 (2000).

[3] See for instance, Papapetrou, A. (1974). Lectures on General Relativity (Dordrecht, Holland)

[4] R. Tolman, Phys. Rev. 35, 875 (1930).

[5] D. E. Vincent, Class. Quantum Grav. 2, 409 (1985).

If we differentiate (2.3) with respect to g^(mn) we obtain

Contraction with gives

Differentiating (3.1) with respect to g^mn leads to

Using these relations a little calculation yields (3.11). For (3.12) the same procedure is used. If we differentiate (2.3) with respect to g^mn,_r and contract with we obtain

Differentiation of (3.1) with respect to g^mn,_r yields

Using these two relations we obtain (3.12).

From (3.10) and (2.6) the expression inside the brackets in (3.23) is given by

With this and the relations

and

where we have used (2.4) for the last term, we obtain

Next we use (2.19) in the first term and write the second one as,

Noting that g_rgg^bg _,a = –g_rg,ag^bg we obtain

Performing the s–differentiation leads directly to equation (3.26).

Taking (B1) into (3.24) leads directly to (3.29).

Using (B1) in the third identity (3.25) gives

where

With the help of (3.12) we obtain

To calculate the first term on the right-hand side of this relation we use (2.10) and make use of (2.12) to write

In this way we obtain

When this is substituted into (B8) we immediately see the cancellation of all the terms involving . The next step is to perform a convenient differentiation by parts of the three terms coming from the first part of the right-hand side of (B11). For the first one we write g^(ar)s_ag,l = , for the second one g^(sg)g^(ar)s_lg,a = – (g^(sg)g^(ar)),_as_lg and a similar decomposition for the third on. After using (3.1) we arrive at

When this is substituted into (B7) the divergence of the last term drops out and, therefore, that equation can be written as in (3.31).

In the weak field linear approximation we set

where h_ab = diag(1,–1,–1,–1) and | h_ab | 1. Thence, g_[ab] = h_[ab] and g^ab = h^ab – h^ba where h^ba = h^bmh^anh_mn. Then g^[ab] = h^ab + h^[ab]. Thence, to lowest order (2.4) and (2.8) become

and

Taking the divergence of (C2), using (C3) and choosing the gauge = 0 leads to the relation

In the time-independent regime we are interested in this gives

with solution

Far away we have

The second integral can be converted into a surface integral surrounding the localized source around the origin and vanishes. Therefore,

For a = 0 the integral is equal to the fermionic charge F. For a = i the integral is null because in the time independent regime the equation of continuity reduces to ¶_iS_i = 0: then ¶_i(x_jS_i) = S_j and, by going to a surface integral of the first term, the integral of the current indeed vanishes. Thence (C8) leads to (4.5). Next, we need h_[ab] far away from the sources which, according to Eq. (C2), is given by

From the previous result we find for the 0i and ij components

which are the content of (4.6).

In the weak field linear approximation we have (C1). Then

and its inverse is s_ab = h_ab + h_(ab). The last term in (2.10) involving the determinants is of the second order because g = –1 – h^abh_ab = –1 – h^abh_(ab) = s, to first order.. From here we see that, to the order considered, reduces to the Christoffel symbol. Therefore U_ab becomes the first-order Ricci tensor and we are in the same situation as in GR. Thence, in harmonic coordinates, (h_ab – h_abh/2)_,^b = 0, the field equation (2.1) reduces to

For time independent fields and noting that Ѳr² = 6 this equation gives

where according to (2.19) the zeroth-order down and upper-indices stress are related by = h_amh_bnT^(0)mn. To the order considered only = r, the mass density, is to survive on the right-hand side. Thence, for the 00 component,

From here follows

For the i0 component (D3) gives h_0i = 0 and for the ij component the result is

Therefore, the non-null metric components are

and

involving the L term as in GR, as stated in the text.

APPENDIX A:  PROOF OF EQUATIONS (3.11) AND (3.12)

APPENDIX B:  PROOF OF EQUATIONS (3.26), (3.29) AND (3.31)

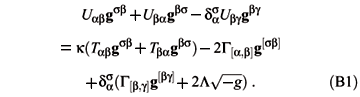
APPENDIX C:  PROOF OF EQUATIONS (4.5) AND (4.6)

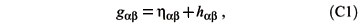
APPENDIX D:  THE LINEAR APPROXIMATION OF (2.1)

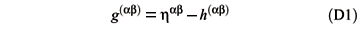
Publication Dates

• Publication in this collection
  17 Jan 2006
• Date of issue
  Dec 2005