Conductance through two quantum dots in a ring: magnetic flux dependence

Abstract

The conductance of a double-dot system in a ring threaded by a magnetic flux is studied. The ring is connected to two leads in such a way that each dot is embedded in one arm of the structure. The currents going through each arm of the ring are determined by the Aharonov-Bohm effect and the dot charging effects. The conductance for different values of the magnetic flux is obtained as a function of the gate potentials applied to the dots, for two situations: when the dot level energies are equal, deltaE = 0, and when they are different but with deltaE smaller than the Coulomb interaction U. The conductance shows quite distinct behavior according to having a finite or zero magnetic flux threading the ring. The system presents S = 1/2 and S = 1 Kondo phenomena for no magnetic flux and is in the S = 1/2 Kondo regime in the case of half a quantum of magnetic flux.

Conductance; Double-dot system; Magnetic flux

NANOSTRUCTURES

Conductance through two quantum dots in a ring: magnetic flux dependence

V. M. Apel^I; Maria A. Davidovich^I; G. Chiappe^II; E. V. Anda^I

^IDepartamento de Física, Pontificia Universidade Católica do Rio de Janeiro, C.P. 38071-970, Rio de Janeiro, RJ, Brazil

^IIDepartamento de Física, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires Ciudad Universitaria, 1428, Buenos Aires, Argentina

ABSTRACT

The conductance of a double-dot system in a ring threaded by a magnetic flux is studied. The ring is connected to two leads in such a way that each dot is embedded in one arm of the structure. The currents going through each arm of the ring are determined by the Aharonov-Bohm effect and the dot charging effects. The conductance for different values of the magnetic flux is obtained as a function of the gate potentials applied to the dots, for two situations: when the dot level energies are equal, DE = 0, and when they are different but with DE smaller than the Coulomb interaction U. The conductance shows quite distinct behavior according to having a finite or zero magnetic flux threading the ring. The system presents S = 1/2 and S = 1 Kondo phenomena for no magnetic flux and is in the S = 1/2 Kondo regime in the case of half a quantum of magnetic flux.

Keywords: Conductance; Double-dot system; Magnetic flux

I. INTRODUCTION

The transport properties of double-quantum-dot systems connected to leads have been experimentally and theoretically investigated in the last years[1] due to their possible technological applications, in particular in quantum computing[2]. When the configuration of the two dots is such that each dot is inserted into one arm of a ring connected to leads, as shown in Fig. 1, there are two paths for the electrons to go through the ring producing interferences that depend upon the phase in each arm. Theoretical[3] and experimental[4] works have studied the transmission phase shifts of single- and double-quantum-dot systems in the independent electron approximation and in Coulomb blockade regime. More recently the effect of Kondo correlation on the transmission phase of a single quantum dot has been measured[5] and theoretically discussed[6, 7]. For the double-dot system in the Kondo regime the effect of the interferences on the spectral densities has been studied[8], taking the intra and inter-dot Coulomb repulsion to be infinite. This limit restricts the study of the Kondo phenomenon and the phase shift interference effects to a situation in which the number of electrons in the system cannot be greater than one.

In our work we study the transport properties of a double-dot system in an Aharonov-Bohm ring when both dots are in the Kondo regime. The ring is connected to leads and threaded by a magnetic flux, the intra-dot Coulomb interaction is taken to be finite and the inter-dot interaction negligible. By varying the magnetic flux and the charge at the dots, controlled by applied gate potentials, different Kondo regimes can be accessed. Depending on the magnetic flux interesting physics appear when both dots are charged and in the Kondo regime.

II. METHOD

An Anderson two-impurity first-neighbor tight-binding Hamiltonian represents the system,

where V_a and V_b are the gate potentials applied to the dots and U is the intra-dot Coulomb repulsion, considered to be equal for the two dots. The parameter t' is the hopping matrix element between the dots and their neighbors in the ring and t the first neighbor hopping within the leads.

The low temperature properties of the system, T < T_K where T_K is the Kondo temperature, can be obtained by calculating the one-particle Green functions G of the system. The many-body problem is treated by exactly diagonalizing a cluster containing the two dots and some lead sites, using a Lanczos algorithm[9]. The Green functions G, obtained by embedding the cluster into the rest of the system, are imposed to satisfy a Dyson equation = +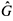

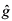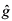
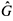where 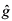is the Green function matrix of the cluster and 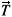is the matrix Hamiltonian that couples the cluster to the rest of the system. Consistency is obtained by imposing the same charge for the dressed and undressed clusters[10]. This approximation has shown to be very accurate when the cluster is of the size of the Kondo cloud hv_f/T_k, where v_f is the Fermi velocity, although it gives qualitatively reliable results even for shorter clusters[11].

The conductance of the system is defined as G = dI/dV where I is the current that flows from the left lead, at a chemical potential µ_L, to the right lead, at a chemical potential µ_R. Denoting by L (R) the site at the left (right) lead nearest neighbor to site (1), shown in Fig 1, the current along the system can be written as,

where t_1R = t is the hopping between nearest neighboring sites in the leads and the G^-+ are nonequilibrium Green functions. Within the Keldysh formalism[12] these functions can be related to the dressed retarded and advanced equilibrium Green functions, G^r and G^a, as

where g^-+ is the density of states of the equilibrium system multiplied by the Fermi distribution functions and , and S^r(a) = t. Using Eq. 3 to obtain (w) and (w) and substituting into Eq. 2 we obtain, after some manipulations, the following expression for the current:

that, at T = 0 reduces to,

In the limit of an infinitesimal bias the linear differential conductance can be expressed as,

where r(e_F), the density of states at the first site of a semi-infinite chain, and the Green function is calculated at the Fermi level.

III. RESULTS AND DISCUSSIONS

The transport properties for different magnetic flux values are obtained as a function of the gate potentials applied to the dots. In units of the Coulomb interaction, U, we take G = 0.05; where G = t¢²/W and W is the leads bandwidth. The Fermi level is at e_F = 0.

The conductance for four values of the magnetic flux, F = 0, F₀/8, F₀/4 and F₀/2, are represented in Fig. 2 (white corresponds to maximum conductance and black, to minimum) as a function of the gate potentials applied to the dots, V_a and V_b. It is interesting to notice the qualitative differences between the case F = 0 and the cases F ¹ 0. They are more striking when the dot level energies are closer, DE ~ 0, that corresponds to the region in the vicinity of the diagonal (continuous line) in Fig. 2. On the other hand, in the regions of the parameter space that correspond to a large difference between the dot level energies the results are weakly dependent upon the magnetic flux. This is reasonable since in these cases the current flows essentially along one arm of the ring since, when one dot is in resonance with the Fermi level the other has either no electrons or two, so that there is only one dot active at a time. In this case the conductance possesses the characteristics of the one-dot conductance with a width, as a function of the gate potential, of the order of U due to the Kondo effect of the charging dot.

Let us focus on the more interesting region -1 < V_a, V_b < 0 of Fig. 2, where the dot energy levels are closer and below the Fermi level. The electrons flow through the two ring arms, and both dots are at resonance since they are in the Kondo regime. For F = 0 the two arm transmissions are in phase and interfere constructively. The conductance as a function of the gate potentials has one broad peak as can be concluded from Fig. 2a. As the magnetic flux is turned on, the currents along the two arms are no longer in phase and the transport properties change qualitatively. For F = F₀/2, the arm transmissions are out of phase and the conductance for DE = 0 cancels out for all values of the gate potentials (see continuous line in Fig.2d).

In Fig. 3 we show the conductance of the system for various magnetic flux values, as a function of V_a for DE = 0 (V_a = V_b) and DE = 0.6 (V_a = V_b - 0.6), corresponding, respectively, to the diagonal continuous lines and dashed lines in Fig. 2.

We first analyze the cases where DE = 0, when the two dot levels have the same energy so that the two ring arms are identical. If there is no magnetic field crossing the ring the arm transmissions always interfere constructively and the conductance as a function of the gate potential V_a shows a large peak since both dots are in the Kondo regime, as depicted in Fig. 3a. On the other hand, the conductance for F = F₀/2 cancels for all values of the gate potentials, as expected since in this case the difference of phase between the transmission in the two arms is Df = p. For 0 < F < F₀/2 the conductance is finite except at the values of the gate potentials such that the system is in the electron-hole symmetry condition (V_a = V_b = -0.5) where it is zero independent of the magnetic flux, as shown in Fig. 3b, for F = F₀/4, F₀/8. This surprising result has also been obtained analytically[13] for the conductance of the same system in the independent electron approximation, that is, neglecting the Coulomb interaction U. It is shown that, for DE = 0 and the system in the electron-hole symmetry condition, the conductance goes discontinuously from its maximum value 2e²/h, at F = 0, to zero, for any other value of the magnetic flux. Moreover, the calculated phase difference between the two arm rings is found to go also discontinuously from zero, for F = 0, to Df = p, for F ¹ 0, in agreement with the conductance results.

The cases with DE = 0.6 are represented in Fig. 3c, for F = 0 and F₀/2, and in Fig. 3d, for F = F₀/20, F₀/8, F₀/4. In these cases the phase difference between the two arm rings is not only due to the Aharonov-Bohm effect but it depends also on the state of charge of the dots that are different. As V_a decreases from the value 0.5 charge begins to enter into dot a and its spin gets correlated to the conduction electron spins. Dot a is in the Kondo regime and the conductance increases up to the maximum value of 2e²/h. As V_a is further decreased dot b begins also to get charged and develops also a Kondo peak. The conductance is symmetric with respect to the gate potential V_a = -0.8, when the two dots are in the electron-hole symmetry condition having just two electrons. The Kondo phenomenon is responsible for the finite conductance in almost the whole range of gate potential.

The dependence of the conductance on V_a is qualitative different for F = 0 as compared to the other values of the magnetic flux. It presents three peaks and cancels out for two values of V_a due to destructive interferences as a result of the different states of charge of the dots. This is in agreement with the Onsager relation according to which the conductance of our system, that possesses a closed geometry, is an even function of the applied magnetic flux. This implies that the phase difference between the two arm transmissions for F = 0 can only have the values Df = 0, p, depending on the gate potentials applied to the dots.

By a qualitative analysis based on perturbation theory we can argue that the cases for F = 0 and F = F₀/ 2 are diverse, as far as the correlation between the dots is concerned. The effective interaction between the dots can be obtained by taking the non-diagonal matrix elements that connect the dots to the rest of the circuit, t¢, as a perturbation. Due to the system topology it is clear that to get the dominant contribution to the effective inter-dot interaction it is necessary to go to forth order in perturbation theory. In this case, while for F = 0 the contributions that go from one dot to the other and return along the same path sum-up with the circulating contributions, for F = F₀/ 2 these two contributions, having opposite signs, tend to cancel each other, giving rise to a weak inter-dot correlation. Therefore, in the central region of the conductance, when the dots have two electrons, the two dot spins would be uncorrelated for F = F₀/2 and strongly correlated for F = 0. Based on this argument the central peak of conductance for F = 0 can be interpreted as due to an S = 1 Kondo state.

IV. CONCLUSIONS

In summary we have studied the conductance of a double-dot system in a ring threaded by a magnetic flux and connected to leads in such a way that each dot is embedded into one arm of the resultant structure. The currents going through each arm of the ring are determined by the Aharonov-Bohm effect combined with the dot many-body charging effects. For two different situations, one where the dot level energy splitting DE = 0 and the other with DE ¹ 0 but smaller than the Coulomb interaction U, we obtain the conductance for various values of the magnetic flux, from F = 0 to F₀/ 2, as a function of the gate potentials applied to the dots. The case for no magnetic flux presents quite different behavior with respect to the other cases where a finite magnetic flux crosses the ring. When both dots are charged with one electron, for F = 0 their spins are ferromagnetically correlated and the conductance presents peaks due to S = 1/2 and S = 1 Kondo regime, while in the case F = F₀/ 2 the dot spins are uncorrelated and the conductance is due to the more familiar S = 1/2 Kondo phenomenon.

V. ACKNOWLEDGEMENTS

We acknowledge the Brazilian Agencies FAPERJ, CNPq and CAPES, the grant Antorchas/Vitae/Andes No. A-13562/1-3, The Argentinian Agency CONICET and Fundacion Antorchas for financial support.

[1] W. G. van der Wiel, S. De Franceschi, M. Elzerman, T. Fujisawa, S. Tarucha, and L. P. Kouwenhoven, Rev. Mod. Phys. 75, 1 (2003); C.A. Busser, E. V. Anda, A. L. Lima, M. A. Davidovich, and G. Chiappe, Phys. Rev. B 62, 9907 (2000); D. Loss and D. P. DiVicenzo, Phys. Rev. A 57, 120 (1998).

[2] D. P. DiVicenzo, Science 720, 255 (1995); G. Burkard, D. Loss, and D. P. DiVicenzo, Phys. Rev. B 59 2070 (1999).

[3] V. Moldoveanu, M. Tolea, A. Aldea, and B. Tanatar, Phys. Rev. B 71, 125338 (2005); A. Aharony, O. Entin-Wohlman, B. I. Halperin, and Y. Imry, Phys. Rev. B 66, 115311 (2002); J. Konig and Y. Gefen, Phys. Rev. Lett. 86, 3855 (2001); A. Y. Smirnov, N. J. M. Horing and L. G. Mourokh, App. Phys. Lett. 77, 578 (2000).

[4] K. Kobayashi, H. Aikawa, S. Katsumoto, and Y. Iye, Phys. Rev. Lett. 88, 256806 (2000); A. W. Holleitner, C. R. Decker, H. Qin, K. Eberl, and R. H. Blick, Phys. Rev. Lett. 87, 256802 (2001); A. Yacoby, M. Heiblum, D. Mahalu, and H. Shtrikman, Phys. Rev. Lett. 74, 4047 (1995).

[5] Y. Ji, M. Heiblum, D. Sprinzak, D. Mahalu, and H. Shtrikman, Science 290, 779 (2000); U. Gerland, J. von Delft, T. A. Costi, and Y. Oreg, Phys. Rev. Lett. 84, 3710 (2000).

[6] A. Aharony, O. Entin-Wohlman, and Y. Imry, Phys. Rev. Lett. 90, 156802 (2003).

[7] W. Hofstetter, J. Konig, and H. Schoeller, Phys. Rev. Lett. 87, 156803 (2001).

[8] D. Boese, W. Hofstetter, and H. Schoeller, Phys. Rev B 66, 125315 (2002); idem 64, 125309 (2001).

[9] E. Dagotto, Rev. Mod. Phys. 66, 763 (1994).

[10] V. Ferrari, G. Chiappe, E. V. Anda, and M. A. Davidovich, Phys. Rev. Lett. 82, 5088 (1999).

[11] C. A. Busser, G. B. Martins, K. A. Al-Hassanieh, A. Moreo, and E. Dagotto, Phys. Rev B 70, 245303 (2004)

[12] L. V. Keldysh, Sov. Phys. JETP 47, 1018 (1965)

[13] V. M. Apel, M. A. Davidovich, and E. V. Anda, to be published

Received on 4 April, 2005

Publication Dates

• Publication in this collection
  06 July 2006
• Date of issue
  June 2006

History

• Received
  04 Apr 2005