Abstract
We investigate the spin dynamics of a magnetic adatom on a non-magnetic surface with strong Stoner enhancement. We find a strong damping of the adatom's magnetization precession and a large shift of the resonance frequency from its bare value. Stoner enhancement in the substrate reduces the damping. We explore the damping dependence on features of the electronic structure.
Spin waves; Giant magnetic moment; Spin current
ELECTRONIC AND MAGNETIC PROPERTIES OF NANOSCOPIC SYSTEMS
Contribution of the spin current to the damping of the magnetic moment precession of Fe impurities in Pd
M. V. Tovar CostaI; A. C. de Castro BarbosaII; A. T. Costa Jr.III
IInstituto de Aplicação, Universidade do Estado do Rio de Janeiro, 20.261-232, Rio de Janeiro, RJ, Brazil
IIInstituto de Matemática e Estatística, Universidade do Estado do Rio de Janeiro, 20.550-013, Rio de Janeiro, RJ, Brazil
IIIDepartamento de Ciências Exatas, Universidade Federal de Lavras, 37.200-000, Lavras, MG, Brazil
ABSTRACT
We investigate the spin dynamics of a magnetic adatom on a non-magnetic surface with strong Stoner enhancement. We find a strong damping of the adatom's magnetization precession and a large shift of the resonance frequency from its bare value. Stoner enhancement in the substrate reduces the damping. We explore the damping dependence on features of the electronic structure.
Keywords: Spin waves; Giant magnetic moment; Spin current
I. INTRODUCTION
The behavior of the Pd-based diluted alloys has attracted much attention since the first experiments indicated the appereance of a giant magnetic moment surrounding the magnetic impurities' sites,[1]. This effect is understood as a consequence of the strong polarization of the host atoms by the impurity, creating a polarization cloud. Experimental results indicate that the susceptibility of Pd has a Stoner enhancement factor of about 10, and one can consider Pd as nearly ferromagnetic. The experimental works with dilluted impurities of Mn, Fe and Co on Pd revealed magnetic moments of, 8µB, 12.6µB, and 10.8µB, respectively, which corresponds extended cloud with a large number of polarized atoms [1].
The recent developments of materials' growth and manipulation techniques have allowed for the fabrication of diverse nanoscopic structures. Magnetism is strongly affected by dimensionality; thus it is expected that magnetic properties of surfaces, ultrathin films and small clusters of atoms are quite diferent from those found in bulk systems. In the case of Fe impurities or adatoms on Pd surface one expects an enhancement of the magnetic moment due to the low coordination number. Few experimental results of Fe on Pd surface are reported. Bergmann using anomalous magnetic hall effect (AHE) [4] concludes that for a concentration lower than 0.3 atomic layers no magnetic moment was observed but for concentrations above 0.5 atomic layers he found a perpendicular magnetization to the surface. Theoretical works were developed to study the behavior of Fe on Pd surface. Mathon, employing a single band tight-binding model [3] and including the coupling between the impurity and the Pd host, obtained as a solution an antiferromagnetic alignment between Fe impurity and Pd substrate. First principle calculations were used to systematically explore the behavior of 3d and 4d impurities on Pd surfaces. Klautau et al. [2] calculated the magnetization profile of the polarization cloud with up to three shells of Pd atoms around the Fe atom, finding strong enhancement of magnetic moment in both Fe impurity and Fe adatom in Pd surface.
Although a reasonable body of work exists on the static properties of magnetic impurities in Pd and the related polarization cloud, the dynamics of this kind of system is much less studied. Besides its intrinsic fundamental interest, dynamical phenomena are also very important for applications. Magnetic relaxation phenomena are specially relevant for the operation of nanoscale devices in which magnetization is switched very fast. Spin fluctuations are also expected to play a fundamental role if such devices are to work at room temperature. Thus, it is desirable to have a good account of the spin dynamics in these nanoscale systems. Here we are interested in the mechanism of spin precession damping known as spin pumping [5,8,9]. It is being currently explored mainly in ultrathin magnetic films attached to non-magnetic substrates [6,10], but of course it should be equally or more relevant to small magnetic clusters attached or embedded in non-magnetic media. Theoretical studies of the spin excitation spectra of a single magnetic impurity attached to a non-magnetic metal [11] revealed a very strong damping of the spin precession accompanied by a sizeable shift of the resonance frequency, compared to the bare Zeeman spliting gµBH0. Those calculations considered, as substrates, metals for which the Stoner enhancement is negligible. If the substrate is Pd its strong Stoner enhancement should produce different dynamical behavior.
In this work we investigate qualitatively the spin dynamics of a magnetic impurity on a substrate with strong Stoner enhancement. We employ a simplified model for the electronic structure of the materials involved that capture the essential physics of the problem. We explore the dependence of the spin precession damping on the relevant parameters of the system.
II. MODEL
We consider a single magnetic adatom on top of a simple cubic surface in the (001) direction. We employ a tight-binding model with a single orbital per atomic site, and nearest-neighbor hopping integral t. We allow the strength of the hopping between the magnetic adatom and the surface to be t', different from the substrate's. Magnetism in the adatom is driven by on-site Coulomb interaction of strength UFe. Occupations of the substrate and adatom were chosen with real materials in mind: Fe for the adatom and Pd for the substrate, although we may easily vary them to investigate the effect of charge transfer. The strong Stoner enhancement of Pd is simulated by an appropriate choice of Fermi level. On-site Coulomb interactions in the Pd sites are also taken in to account. However, the density of states for the chosen Fermi level is not enough to satisfy the Stoner criterion.
The damping of spin motions in ferromagnetic structures can be investigated experimentally by ferromagnetic resonance (FMR). In a typical FMR experiment, a static uniform magnetic field
0 is applied to the sample, and a circularly polarized harmonic magnetic field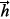 (
(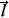 ,t) = (
,t) = (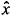 +i
+i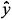 )h(
)h(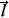 )eiWt is applied in a direction perpendicular to the magnetization. In linear response the resulting transverse magnetization in site
)eiWt is applied in a direction perpendicular to the magnetization. In linear response the resulting transverse magnetization in site 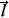 is
is
The susceptibility c(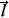 ,
,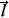 ';W) above is the same whose imaginary part gives the spectrum of spin excitations,
';W) above is the same whose imaginary part gives the spectrum of spin excitations,
Here 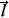 ,
,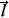 ' are site coordinates, Q is the unit step function and S+(
' are site coordinates, Q is the unit step function and S+(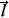 )(S(
)(S(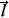 )) is the spin raising (lowering) operator at site
)) is the spin raising (lowering) operator at site 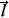 . In what follows we employ a random phase approximation (RPA) to calculate the susceptibility c+, based on a self-consistent mean-field ground state.
. In what follows we employ a random phase approximation (RPA) to calculate the susceptibility c+, based on a self-consistent mean-field ground state.
To limit the complexity of the system we initially restrict the extension of the polarization cloud to the first nearest neighbor of the Fe impurity. This is done by setting UPd = 0 all over the substrate except for the mentioned nearest neighbor.
III. RESULTS AND CONCLUSIONS
We start by showing a typical excitation spectrum in Fig. 1. The quantity we plot is All'(W) = Á{c+(l,l';W)}; the indices l,l' = 1,2 indicate the enhanced Pd site (1) or the Fe impurity site (2). In this case t = t' = 1, UFe = 10, UPd = 8. We chose the strength of Coulomb interaction in Fe so that Stoner criterion is satisfied at the impurity site. First principle calculations [7] indicate that UPd ~ 0.8UFe. The static field H0 is such that  = gµBH0 = 1×10-2 in our energy units (we take the substrate's hopping integral as our energy unit). This spectrum has a lorentzian shape of appreciable width, DW/W0 = 0.26, indicating a strongly damped spin precession [12]. Since our hamiltonian is invariant under rigid rotation of all the spins in the system, damping of local precession can olnly come from transfer of spin angular momentum from the local moment to the sea of conduction electrons. This is precisely the spin-pumping mechanism referred to in the introduction. Also noticeable is the large shift in the resonance frequency from the bare value
= gµBH0 = 1×10-2 in our energy units (we take the substrate's hopping integral as our energy unit). This spectrum has a lorentzian shape of appreciable width, DW/W0 = 0.26, indicating a strongly damped spin precession [12]. Since our hamiltonian is invariant under rigid rotation of all the spins in the system, damping of local precession can olnly come from transfer of spin angular momentum from the local moment to the sea of conduction electrons. This is precisely the spin-pumping mechanism referred to in the introduction. Also noticeable is the large shift in the resonance frequency from the bare value  . This can be understood if we think of the damping as a complex self-energy added to the denominator of the spin susceptibility; the self energy's imaginary part is responsible for the damping, its real part shifts the resonance frequency. The larger the damping larger the frequency shift.
. This can be understood if we think of the damping as a complex self-energy added to the denominator of the spin susceptibility; the self energy's imaginary part is responsible for the damping, its real part shifts the resonance frequency. The larger the damping larger the frequency shift.
In the same Fig. 1 we show the case of a substrate in which there is no Stoner enhancement, corresponding to letting UPd = 0. The increase in linewidth is small but noticeable, indicating a larger damping. Thus, the magnetic moment induced in the Stoner enhanced Pd substrate serves as a ''trap'' for the flux of transverse spin leaking from the precessing Fe magnetic moment.
A virtue of our simple tight-binding model is that we have flexibility to test sensitivity of the calculated results to features of the electronic structure, if desired. In view of the preceding analysis, it is interesting to see how a variation of the Stoner enhancement in Pd affects the damping of the Fe adatom's magnetic moment. In Fig. 2 we plot the linewidth of the spectral density A22(W) as a function of UPd. As the enhancement increases the magnetic moment in the Pd site also increases, becoming a more efficient trap for the magnetic moment leaking from the Fe adatom; thus the damping decreases. The behavior of  (Fig. 3) favors this analysis. This component of the spectral density gives the precession amplitude induced in the Pd site by a field applied to the Fe adatom, as indicated by eq. 1. As the Stoner enhancement increases so does the precession amplitude at the enhanced Pd site. This corresponds to an effective increase in the ferromagnetic part of the sample, which leads to a smaller overall damping. A similar behavior is observed in ultrathin ferromagnetic films as a function of film thickness N: the damping decreases roughly as 1/N [10].
(Fig. 3) favors this analysis. This component of the spectral density gives the precession amplitude induced in the Pd site by a field applied to the Fe adatom, as indicated by eq. 1. As the Stoner enhancement increases so does the precession amplitude at the enhanced Pd site. This corresponds to an effective increase in the ferromagnetic part of the sample, which leads to a smaller overall damping. A similar behavior is observed in ultrathin ferromagnetic films as a function of film thickness N: the damping decreases roughly as 1/N [10].
The interpretation of the damping as resulting from a flux of spin angular momentum towards the substrate suggests that the strength of the hopping integral t' between the adatom and the substrate should play an important role in the determination of the intensity of the damping. In Fig. 4 we plot the linewidth of the spectral density A22(W) as a function of t' for fixed UPd = 8. It shows the damping decreasing as t' increases, contrary to what one's intuition might indicate. However, analysing the dependence of the magnetic moment at the enhanced Pd site on t' one sees that it increases rather strongly; as seen before, a larger mPd means a more efficient trap for the spin current emanating from the Fe site, thus a smaller damping. In this case the increased mPd more than compensates for the increase in connectivity between the adatom and substrate that would facilitate the flux of spin current, thus increasing the damping.
Acknowledgments
M.V.T.C. and A.C.C.B. aknowledges the Depesq/UERJ for partial finnancial support. A.T.C. acknowledges financial support from CNPq.
[1] F W. Constant, Phys. Rev., 36, 1654 (1930); G. G. Low, Proc. Phys. Soc. Lond, 89, 119 (1968); G. J. Nieuwenhuys, Adv. Phys., 24, 515 (1975).
[2] A.B. Klautau, P.R. Peduto, and S. Frotta-Pessoa, J. Magn. Magn. Mater. 186, 223 (1998).
[3] M. Afisharnaderi and J. Mathon, J. Phys. 12-C8, 164 (1988).
[4] G. Bergmann, Phys. Rev. B 23, 3805 (1981).
[5] L. Berger, Phys. Rev. B 54, 9353 (1996).
[6] Y. Tserkovniak et al., Phys. Rev. Lett 88, 117601 and Phys. Rev. B 66, 224403 (2002).
[7] F.J. Himpsel, J. Magn. Magn. Mater. 102, 261 (1991).
[8] J. Slonczewski, J. Magn. Magn. Mater. 102, 195, L261 (1999).
[9] D.L. Mills, Phys. Rev. B 68, 014419 (2003).
[10] A.T. Costa, R.B. Muniz, and D.L. Mills, submitted to Phys. Rev. B.
[11] R.B. Muniz and D.L. Mills, Phys. Rev. B 68, 224414 (2003).
[12] For the sake of comparison, the same kind of calculation for a ultrathin ferromagnetic film on a non-magnetic substrate yield values one to two orders of magnitude smaller.
Received on 8 December, 2005
- [1] F W. Constant, Phys. Rev., 36, 1654 (1930);
- G. G. Low, Proc. Phys. Soc. Lond, 89, 119 (1968);
- G. J. Nieuwenhuys, Adv. Phys., 24, 515 (1975).
- [2] A.B. Klautau, P.R. Peduto, and S. Frotta-Pessoa, J. Magn. Magn. Mater. 186, 223 (1998).
- [3] M. Afisharnaderi and J. Mathon, J. Phys. 12-C8, 164 (1988).
- [4] G. Bergmann, Phys. Rev. B 23, 3805 (1981).
- [5] L. Berger, Phys. Rev. B 54, 9353 (1996).
- [6] Y. Tserkovniak et al., Phys. Rev. Lett 88, 117601
- and Phys. Rev. B 66, 224403 (2002).
- [7] F.J. Himpsel, J. Magn. Magn. Mater. 102, 261 (1991).
- [8] J. Slonczewski, J. Magn. Magn. Mater. 102, 195, L261 (1999).
- [9] D.L. Mills, Phys. Rev. B 68, 014419 (2003).
- [10] A.T. Costa, R.B. Muniz, and D.L. Mills, submitted to Phys. Rev. B.
- [11] R.B. Muniz and D.L. Mills, Phys. Rev. B 68, 224414 (2003).
Publication Dates
-
Publication in this collection
29 Nov 2006 -
Date of issue
Sept 2006
History
-
Received
08 Dec 2005








