Neutral kaon correlations in <FONT FACE=Symbol>Ö</FONT>S NN = 200 GeV Au+Au collisions at RHIC

Abstract

Results from two-K0s interferometry in <FONT FACE=Symbol>Ö</FONT>S NN = 200 GeV Au+Au collisions at RHIC are presented. A model that takes into account the strong final state interaction has been used to fit the data. The effect of coupled K0$\bar{K}$0 and K+K- channels was studied. The value of the correlation radius parameter obtained is consistent with the transverse mass (mT) systematics established in pion correlation measurements.

Neutral Kaon Interferometry

Neutral kaon correlations in ÖS_NN = 200 GeV Au+Au collisions at RHIC

Selemon Bekele^I; Richard Lednický^II,III

^IDepartment of Physics, The University of Kansas, Lawrence, KS 66045

^IIJoint Institute for Nuclear Research, Dubna, Moscow Region, 141980, Russia

^IIIInstitute of Physics ASCR, Na Slovance 2, 18221 Prague 8, Czech Republic

ABSTRACT

Results from two-K⁰_s interferometry in ÖS_NN = 200 GeV Au+Au collisions at RHIC are presented. A model that takes into account the strong final state interaction has been used to fit the data. The effect of coupled K⁰$\bar{K}$⁰ and K⁺K^- channels was studied. The value of the correlation radius parameter obtained is consistent with the transverse mass (m_T) systematics established in pion correlation measurements.

Keywords: Neutral Kaon Interferometry

I. INTRODUCTION

A phase transition from hadronic matter to a new state of matter called a Quark Gluon Plasma (QGP) is predicted to occur at sufficiently large energy densities by Lattice QCD calculations [1]. The primary goal of the heavy-ion collisions program at the Relativistic Heavy-Ion Collider (RHIC) is the creation and study of such a de-confined state of matter. It is believed that a first order phase transition from the QGP back to normal hadronic matter delays the expansion of the hot reaction zone created in the collision [2]. A long duration of particle emission due to a delayed expansion should reveal itself as a large effective source size.

One of the important goals in high energy experiments for the last several decades has been the measurement of the space-time extent of the particle emitting region [3-5]. These measurements are based on the sensitivity of particle momentum correlations to the space-time separation of the particle emitters due to the effects of quantum statistics (QS) and final state interaction (FSI). The QS symmetrization (antisymmetrization) is usually the dominant source of the correlation for identical particles. Due to the interference of the amplitudes corresponding to various permutations of identical particles, the measurement of the corresponding correlation is often called particle interferometry (see [6] for a review).

Because of their smaller mass, pions are the most abundant particles produced in heavy ion collisions. A significant fraction of them, however, come from the decay of unstable resonances after freezout thus complicating the pion interferometry measurements. As a result, while the direct pion source may be inherently non-Gaussian, the resonances extend the source size due to their finite lifetime, introduce an additional essentially non-Gaussian distortion in the two-pion correlator and reduce the fitted correlation strength. Due to the resonance decay phase-space, secondary pions populate mainly the low momentum region and can thus introduce an additional pair momentum dependence of the two-particle correlator.

In contrast to the pions, kaon interferometry suffers less from resonance contributions and could provide a cleaner signal for correlation studies than pions [7,8]. Since the kaon density is considerably smaller than the pion density at RHIC ( = 200 GeV), higher multi-particle correlation effects, that might play a role for pions, should be of minor importance for kaons. For example, the pion multiplicity has increased by approximately 70% from the SPS( = 17.3 GeV) to RHIC [9] but the interferometry radii remain almost the same [10,11]. The strangeness distillation mechanism [12] might further increase any time delay QGP signature. This mechanism could lead to strong temporal emission asymmetries between kaons and anti-kaons [13], thus probing the latent heat of the phase transition.

Particle identification for pions, via their specific ionization (energy loss per unit length or dE/dx), works only up to about 700 MeV/c. Neutral kaons, on the other hand, can be identified up to much higher momentum using their decay topology. This allows for the extension of the interferometry systematics to a higher momentum than is presently achievable with pions, and thus provides a means to probe the earlier times of the collision. The effect of two-track resolution, which is a limiting factor in charged particle correlations, is also small. The absence of Coulomb FSI suppression together with small contributions from resonance decays make neutral kaon correlations a powerful tool to investigate the space time structure of the particle emitting source.

The OPAL [14] and ALEPH [15] collaborations have measured correlations of neutral kaons from hadronic decays of Z⁰ in e⁺e^- collisions at LEP. The WA97 experiment at CERN [16] attempted to measure correlations but did not see a significant enhancement of neutral kaon pairs in the region of small momentum difference due to a lack of sufficient statistics. In this paper, recent results are presented on two- correlations in central Au-Au collisions at = 200 GeV measured by the STAR(Solenoidal Tracker at RHIC) experiment at RHIC [17].

II. CORRELATION FUNCTIONS

The two-particle correlation function C(p₁,p₂) is usually defined as the ratio of the measured two-particle distribution to the reference one obtained by mixing particles from different events of a given class, normalized to unity at sufficiently large relative momenta. The space-time information contained in the momentum correlations is usually extracted based on the following assumptions:

(i) The mean freeze-out phase space density áfñ is assumed sufficiently small so that only the mutual QS and FSI effects can be considered when calculating the correlation function of two particles emitted with a small relative momentum Q = 2k* in their center-of-mass (c.m.) system. It is found that áfñ increases with energy and for central lead-lead or gold-gold collisions seems to saturate at the highest SPS energy [6]. The saturated áfñ is substantially smaller than unity for pions with p_t > 0.2 GeV/c so pointing to negligible multiboson effects in this p_t-region.

(ii) The momentum dependence of the one-particle emission probabilities is assumed inessential when varying the particle four-momenta p₁ and p₂ by the amount characteristic for the correlations due to QS and FSI. This smoothness assumption, requiring the components of the mean space-time distance between particle emitters much larger than those of the space-time extent of the emitters, is well justified for heavy ion collisions.

(iii) An independent or incoherent particle emission is assumed. This assumption is quite reasonable for a dominant part of particle pairs produced in heavy ion collisions and is consistent with the observed strength of two- and three-pion correlation functions (see, e.g., [18-20]).

(iv) To simplify the calculation of the FSI effect, the Bethe-Salpeter amplitude describing two particles emitted at space-time points x_i = {t_i,r_i} and detected with four-momenta p_i is usually calculated at equal emission times in the pair c.m. system. In this approximation, the reduced non-symmetrized Bethe-Salpeter amplitude (with the removed unimportant phase factor due to the c.m. motion), depending only on the relative four-coordinate Dx º x₁ - x₂ = {t,r} and the generalized relative momentum = q - P(qP)/P² (q = p₁ - p₂, P = p₁ + p₂ and qP = m₁² - m₂²; in the two-particle c.m. system, P = 0, = {0,2k*} and Dx = {t*,r*}), is substituted by a stationary solution (r*) of the scattering problem. The solution at large distances r* has the asymptotic form of a superposition of the plane and outgoing spherical waves (the minus sign of the vector k* corresponds to the reverse in time direction of the emission process). This equal time approximation is usually satisfied for heavy particles like kaons or nucleons and, for pions, it merely leads to a slight overestimation (typically < 5%) of the strong FSI effect [21].

The two-particle correlation function then reduces to the square of the two-particle wave function averaged over the distance r* of the emitters in the two-particle c.m. system:

for identical particles, the amplitude in Eq. (1) enters in a symmetrized form. Particularly, for spin-0 bosons,

The two-particle approximation in (i) and FSI separation in the Bethe-Salpeter amplitudes of the elastic transitions a + b ® a + b implies a long FSI time as compared with the characteristic production time, i.e. the c.m. momentum k* much less than typical production momentum transfer of hundreds MeV/c. In fact, the long-time FSI can be separated also in the inelastic transitions, a + b ® c + d, characterized by a slow relative motion in both entrance and exit channels [21,22]. Particularly, calculating the FSI effect on neutral kaon correlations, one has to take into account the coupled K⁺K^--channel (see section IV).

For non-interacting particles, the non-symmetrized wave function reduces to the plane wave, (r*) = exp(-ik*r*) , and the correlation function of two identical spin-0 bosons becomes

Particularly, for the Gaussian distribution of the vector r* of the relative distance between particle emission points in the pair c.m. system:

the correlation function takes the Gaussian form:

where Q = (-q²)^1/2 = 2k*.

The Gaussian expression in Eq. (5) is often used to fit the one-dimensional correlation functions of two identical pions or kaons in a modified form:

where N and l are respectively the normalization and correlation strength parameters. The parameter l equals unity for a fully chaotic Gaussian source and is smaller than unity for a source with partially coherent particle emission. The value of l can also be lowered by the non-Gaussian form of the correlation function, the contribution from kaons coming from long lived resonances. Also neglecting FSI can affect (suppress or enhance) the value of this parameter.

III. THE SYSTEM OF TWO NEUTRAL KAONS

The production of the neutral kaons, K⁰ and 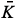⁰, is attributed to the strong interaction which conserves the strangeness quantum number. An interesting property of neutral kaons is that the K⁰ can change into a 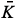⁰ through a second order weak interaction. However, the particles that we normally observe through weak decay channels in the laboratory are not K⁰ and 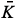⁰ [23]. Neglecting the effects of CP violation, the observed weak interaction eigenstates are given by

where |ñ and |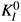ñ are the state vectors of the short and long lived neutral kaons, to which experiments have access via measurements of their decay products, which are mainly pions. The state vector of the system is then given by the expression

Now, if a

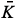pair comes from K⁰K⁰ (⁰

⁰), it is subject to Bose-Einstein (BE) enhancement as it originates from an identical boson pair. On the other hand, the K⁰ and 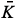⁰ are two different particles and one may not expect correlations if one comes from K⁰ and the other one from 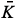⁰. Nevertheless, it can be shown [24] (see also [25-27]) that only the symmetric part of the K⁰

⁰ amplitude contributes to the system and thus also leads to a Bose-Einstein enhancement at small relative momentum (on the contrary, only the anti-symmetric part of the K⁰

⁰ amplitude contributes to the 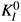system and leads to the "Fermi-Dirac like" suppression). The correlation thus includes a unique interference term that may provide additional space-time information.

The strong FSI has an important effect on neutral kaon correlations due to the near threshold resonances, f₀(980) and a₀(980) [28]. These resonances contribute to the K⁰

⁰ channel and lead to the s-wave scattering length dominated by the imaginary part of ~ 1 fm. Based on the predictions of chiral perturbation theory for pions [29], the non-resonant s-wave scattering lengths ~ 0.1 fm for both K⁰

⁰ and K⁰K⁰ channels and can be neglected to a first approximation.

To calculate the

correlation function, the K⁰'s and 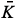⁰'s are assumed to be emitted by independent single-kaon sources so that the fraction of pairs originating from K⁰

⁰ system is a = (1 - e²)/2, where e is the K⁰-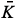⁰ abundance asymmetry. The correlation function is calculated as a mixture of the average squares of the properly symmetrized K⁰K⁰, 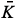⁰

⁰ and non-symmetrized K⁰

⁰ wave functions, weighted by the respective fractions. To average over the relative distance vector r*, the Lednický & Lyuboshitz analytical model [28] has been used, assuming r* is distributed according to Eq. (4) with a Gaussian radius R. The model assumes that the non-symmetrized wave functions Y_-k*(r*) describing the elastic transitions can be written as a superposition of the plane and spherical waves, the latter being dominated by the s-wave,

where k* º Q/2 is the three-momentum of one of the kaons in the pair rest frame and f(k*) is the s-wave scattering amplitude for a given system. Neglecting the scattered waves for the K⁰K⁰ and 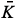⁰

⁰ systems (the corresponding f(k*) = 0) one obtains the following expression for the correlation function [28]:

where F₁(z) = and F₂(z) = . The s-wave K⁰

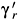⁰ scattering amplitude f(k*) is dominated by the near threshold s-wave isoscalar and isovector resonances f₀(980) and a₀(980) characterized by their masses m_r and respective couplings g_r and to the 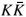,pp and 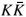,ph channels. Associating the amplitudes f_I at isospin I = 0 and I = 1 with the resonances r = f₀ and a₀ respectively, one can write [28,30]

Here s = 4 and denotes the momentum in the second (pp or ph) channel with the corresponding partial width .

There is a great deal of uncertainty in the properties of these resonances due to insufficiently accurate experimental data and the different approaches used in their analysis. Fortunately, the dominant imaginary part of the scattering amplitude is basically determined by the ratios of the f₀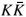 to f₀pp and a₀ 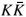to a₀ph couplings whose variation is rather small [31]. In this paper, the resonance masses and couplings from (a) Martin et al. [30], (b) Antonelli [32], (c) Achasov et al. [33], (d) Achasov et al. [33] (see Table I) are used to demonstrate the impact of their characteristic uncertainties on the calculated correlation function.

IV. THE EFFECT OF THE K⁺K^- ® K⁰

⁰ TRANSITION

The interaction of final state particles can proceed not only through the elastic transition ab ® ab but also through inelastic reactions of the type cd ® ab, where c and d are also final state particles of the production process. The FSI effect on particle correlations is known to be significant only for particles with a slow relative motion. Such particles continue to interact with each other after leaving the domain of particle production and their slow relative motion guarantees the possibility of the separation (factorization) of the amplitude of a slow FSI from the amplitude of a fast production process. For the relative motion of the particles involved in the FSI to be slow, the sums of the particle masses in the entrance and exit channels should be close to each other [22]. Thus, in our case, one should account for the effect of inelastic transition K⁺K^- ® K⁰

⁰ in addition to the elastic transition K⁰

⁰® K⁰

⁰. Instead of a single channel Scrödinger equation one should thus solve a two-channel one. In solving the standard scattering problem, one should take into account that the FSI problem corresponds to the inverse direction of time. As a result, one has to make the substitution k* ® -k* and consider K⁰

⁰(º 1) as the entrance channel and K⁺K^-(º 2) as the exit channel. Since the particles in both channels are members of the same isospin multiplets, one can assume that they are produced with about the same probability. Therefore the correlation function will be simply a sum of the average squares of the wave functions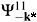 (r*) and 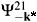(r*) describing the elastic and inelastic transitions respectively.

Assuming the s-wave dominance and r* outside the range of the strong interaction potential, one has [22]:

where µ₁ = /2 and µ₂ = /2 are the respective reduced masses in the two channels. r₂ = , h₂ = ()^-1 and = [2µ₂(k*²/(2µ₁) + 2 - 2]^1/2 is the K⁺ momentum in the two-kaon rest frame; a₂ = -(µ₂e²)^-1 = - 109.6 fm is the (negative) K⁺K^- Bohr radius, (k*) is the s-wave transition amplitude re-normalized by Coulomb interaction in the K⁺K^- channel, (r,h) = . [G₀(r,h) + iF₀(r,h)] is the combination of the singular and regular s-wave Coulomb functions G₀ and F₀. Finally A_c(h) = 2ph/[exp(2ph) - 1] is the Coulomb penetration (Gamow) factor.

The wave function of the elastic transition 1 ® 1 is still given by Eq. (9) in which k* º and the amplitude f = is now the element of a 2 × 2 matrix

Here is a symmetric matrix and _c is a diagonal matrix in the channel representation: = k*, = A_c(h₂) - 2ih(h₂)/a₂, where the function h(h) is expressed through the digamma function y(z) = G'(z)/G(z) as h(h) = [y(ih) - y(-ih) - lnh²]/2. Assuming that the isospin violation arises solely from the mass difference and Coulomb effects on the element , making it different from the momentum k* in the neutral kaon channel, one can express the ^-1 matrix, in the channel representation through the inverse diagonal elements of the -matrix in the representation of total isospin I (the products of the corresponding Clebsch-Gordan coefficients being 1/2 or -1/2):

The latter are assumed to be dominated by the resonances r = f₀(980) and a₀(980) for I = 0 and 1, respectively, so:

One should also take into account the correction due to the deviation of the spherical waves from the true scattered waves in the inner region of the short-range potential, which is of comparable size to the effect of the second channel. This correction is also given in Ref. [22] and is represented in a compact form in Eq. (125) of Ref. [21]. In the case of the kaons,

where = 2Âd(^-1)^ij/dk*²; at k* = 0, ₀ coincides with the real part of the matrix of effective radii.

One may see from Eqs. (10) and (13) that the usual resonance Breit-Wigner behavior settles only at small r* when squares of the spherical waves |/r*|² dominate. At sufficiently large k*, one can neglect the Coulomb effects and put (f₀ + f₁)/2, (f₀ - f₁)/2, so that ||² + ||² |f₀|² + |f₁|². The sum of the square terms then reduces to the incoherent Breit-Wigner contributions of f₀ and a₀ resonances. There can also be additional (not related to FSI) resonance contribution of the usual Briet-Wigner form due to direct f₀(980) and a₀(980) production. This contribution is assumed to be negligible as compared to the FSI effect.

In the fits, the normalization and correlation strength parameters N and l are taken into account by the substitution C(Q) ® N·[l·C(Q) + (1 - l)]. Figure 1 shows the theoretical correlation functions [17] for two sets of resonance parameters from Table 1 with R = 6 and R = 3 fm as input radii with the normalization factor N and l both set to unity.

The results indicate that the effect of the strong FSI in the K⁰

⁰ system is to give rise to a repulsive-like component causing the correlation function to go below unity.

V. THE EXPERIMENTAL CORRELATION FUNCTION

The data used in the present analysis were collected using the Solenoidal Tracker at RHIC(STAR)[35]. The STAR detector consists of several detector subsystems in a large solenoidal magnet that provides a uniform 0.5 Tesla field. The main setup consisted of the time projection chamber (TPC) [36] for charged particle tracking, a scintillator trigger barrel (CTB) surrounding the TPC for measuring charged particle multiplicity, and two zero degree calorimeters (ZDC) [37] located upstream and downstream along the axis of the TPC and beams to detect spectator neutrons. With full azimuthal coverage over |h| < 1 and an almost 100% efficiency for minimum ionizing particles, the CTB provides a good estimate of the number of charged particles produced in the mid-rapidity region. The number of neutrons detected in the ZDC's is identified with the amount of energy deposited in them. The collision centrality is determined by correlating the energy deposition in the ZDC with the number of minimum ionizing particles detected by the CTB. Events from the ZDC and CTB central trigger (0 - 10% of the total hadronic cross section) data sets were used with an event vertex within ±25 cm of the center of the TPC along the beam axis.

The has a mean decay length (ct) of 2.7 cm and decays via the weak interaction into p⁺ and p^- with a branching ratio of about 68%. The mass and kinematic properties of the are determined from the decay vertex geometry and daughter particle kinematics [34]. Neutral kaon candidates are formed out of a pair of positive and negative tracks whose trajectories point to a common secondary decay vertex which is well separated from the primary event vertex.

Figure 2 shows the invariant mass distribution of the neutral kaons [17]. The background below peak is characterized by a polynomial fit to the distribution outside the mass peak. This enables us to define the purity S/(S + B) (ratio of signal to signal plus background) of the sample in the reconstructed mass peak. The observed mass 495.6±6.8 MeV/c² is consistent with the accepted value [38]. The signal and background for the mass range from 0.48 GeV/c² to 0.51 GeV/c² considered in this analysis are shown by the shaded regions. All neutral kaon candidates, with invariant masses from 0.48 GeV/c² to 0.51 GeV/c², transverse momentum from 0.5 GeV/c to 3.5 GeV/c and rapidity between -1.5 and 1.5 have been considered. The daughter particle tracks are required to have a minimum of 15 TPC hits and a distance of closest approach to the primary vertex greater than 1.3 cm.

Experimentally, the two-particle correlation function is defined as

where A(Q) represents the distribution of the invariant relative momentum Q for a pair of particles from the same event. The possibility of a single neutral kaon being correlated with itself, i.e., correlation between a real and a fake reconstructed from a pair which shares a daughter of the real , was eliminated by requiring that kaons in a pair have unique daughters. The effects from splitting of daughter tracks have also been explored by looking at the angular correlation between the normal vectors to the decay planes of the in a given pair. No enhancement at very small angles was observed indicating no significant problem from track splitting. B(Q) is the reference distribution constructed by mixing particles from different events with similar Z-vertex positions(relative z position within 5 cm). The individual for a given mixed pair are required to pass the same single particle cuts applied to those that go into the real pairs. The mixed pairs are also required to satisfy the same pairwise cuts applied to the real pairs from one event. The efficiency and acceptance effects cancel out in the ratio .

The effect of momentum resolution on the correlation functions has also been investigated using simulated tracks from decays with known three-momenta, p_in, embedded into real events. The embedded tracks were simulated taking into account the response of the TPC and scattering effects. The resolution in p lies between 1% and 2% for the p_T range used in this analysis.

The top panel in Figure 3 shows the K_T distribution for Q < 0.2 GeV/c where K_T = (|p_1T + p_2T|)/2. One can see that the shape of the K_T distribution changes with the pair purity and, as a result, so does áK_Tñ, the mean of the distribution. The mean K_T varies almost linearly with pair purity. For the lowest pair purity value of » 52%, áK_Tñ » 0.805 GeV/c. At the highest pair purity value of » 89%, áK_Tñ » 1.07 GeV/c [17]. The dependence of áK_Tñ on the pair purity together with the fact that the radii may vary with K_T implies that varying the pair purity may change the measured radii. In this analysis, the correlation function is integrated over all K_T since the statistics are not sufficient to make a K_T dependent study.

Corrections to the raw correlation functions were applied according to the expression

where the pair purity was calculated as the product of the signal(S) to signal plus background (S + B) ratios of the two of the pair (i,j)

The pair purity, PairPurity(Q), has been found to be independent of Q over the range of invariant four-momentum difference considered. As a result, an average value over Q of the pair purity has been used to correct the correlation function.

Figure 4 shows the experimental correlation function before and after corrections for purity and momentum resolution are applied [17]. It has been verified that the correlation function due to pairs coming outside the mass window is flat. It can be seen that the effect of momentum resolution is comparable to that of purity correction.

VI. EXPERIMENTAL RESULTS

The experimental correlation functions are fit using the Lednický & Lyuboshitz [28] model to take into account the effect of the strong FSI. The free parameters are the radius R characterizing the separation r* of the particle emission points in the pair rest frame, the normalization N, and l. This fitting was done assuming the Gaussian r*-distribution of Eq. (4).

Figure 5 shows an example of the model fits to the experimental correlation function. A Gaussian fit to the correlation function gives R = 5.02±0.61 fm and l = 1.08±0.29. One can see that a Gaussian fit cannot account for the C(Q) < 1 part of the data which are fit better if the strong FSI is included. When taking the effects of the strong FSI, the values obtained are R = 4.09±0.46(stat.)±0.31(sys) fm and l = 0.92±0.23(stat)±0.13(sys) at the mean transverse mass ám_Tñ = 1.07 GeV [17]. The value of l is consistent with unity as expected for a chaotic system with little contributions from decaying resonances. Plotting the radius as a function of the mean K_T, as shown in Figure 6, shows a slight dependence of R with increasing K_T [17]. However this could be a remaining artifact of the mean K_T dependence on pair purity, as mentioned earlier and shown in Figure 3. One has to look at several K_T bins for a specified pair purity to study a K_T dependence of the radius coming from real physics effects. This was not possible in this analysis due to the limited statistics.

Figure 7 shows the m_T dependence of R extracted from pp [39], [17], and proton-L correlations [40]. Considering the large mean transverse momentum of the pair, the value of R for before taking into account the FSI in the K⁰

⁰ system is larger than expected from the systematics followed by the rest of the data. However, after taking into account the FSI effect the neutral kaons also seem to follow the m_T scaling that hydrodynamics predicts [41].

VII. CONCLUSIONS

The first measurement of neutral kaon correlations in heavy-ion collisions at RHIC are presented. To obtain reasonable agreement between theory and data, the effect of the strong FSI has to be considered. The variations of the resonance parameters result in very small differences, which are well within the systematic errors. A Gaussian fit to the correlation function does not account very well for the C(Q) < 1 part of the data and gives a radius which is larger compared to the model fit results.

The measured correlation radius for the neutral kaon is intermediate between those obtained from two-pion and proton-lambda correlations in these collisions with the same conditions except for a different transverse mass, m_T. The radii seem to follow a universal m_T dependence in agreement with a universal collective flow predicted by hydrodynamics. The value of the parameter l has been found to be consistent with unity and thus points to a chaotic kaon source. This is in correspondence with an indication of a dominantly chaotic pion source obtained from STAR measurement of three-pion correlations [18].

Small contributions from resonance decays, the fact that the Coulomb interaction is absent in the dominant elastic transition and that the strong FSI effect can be handled with sufficient accuracy makes neutral kaon interferometry a powerful tool which allows for an important cross-check of charged pion correlation measurements.

The results presented represent an important first step towards a multi-dimensional analysis of neutral kaon correlations using the high statistics data from RHIC. In the future this analysis will allow to extract information about the freeze-out geometry, collective flow velocity, the evolution time and duration of particle emission. The latter is especially interesting in the context of an increased emission duration expected if there is a first order phase transition from a quark gluon plasma to a hadronic system. Recent pion interferometry measurements at RHIC however point to a smaller evolution time and emission duration than expected from the usual hydrodynamic and transport models. This result may indicate an explosive character of the collision and is often considered as the interferometry puzzle.

Acknowledgements

We thank the RHIC Operations Group and RCF at BNL, and the NERSC Center at LBNL for their support. This work was supported in part by the Offices of NP and HEP within the U.S. DOE Office of Science; the U.S. NSF; the BMBF of Germany; CNRS/IN2P3, RA, RPL, and EMN of France; EPSRC of the United Kingdom; FAPESP of Brazil; the Russian Ministry of Science and Technology; the Ministry of Education and the NNSFC of China; IRP and GA of the Czech Republic, FOM of the Netherlands, DAE, DST, and CSIR of the Government of India; Swiss NSF; the Polish State Committee for Scientific Research; SRDA of Slovakia, and the Korea Sci. & Eng. Foundation. It has been partly carried out within the scope of the GDRE: Heavy ions at ultrarelativistic energies -a European Research Group comprising IN2P3/CNRS, EMN, University of Nantes, Warsaw University of Technology, JINR Dubna, ITEP Moscow and BITP Kiev.

[1] F. Karsch, Z. Phys. C 38, 147 (1988); F. Karsch, hep-lat/0106019.

[2] S. Pratt et al., Phys. Rev. C 42, 2646 (1990).

[3] M.I. Podgoretsky, Sov. J. Part. Nucl. 20, 266 (1989).

[4] U.A. Wiedemann and U. Heinz, Phys. Rept. 319, 145 (1999).

[5] R. Lednicky, Phys. At. Nucl. 67, 72 (2004).

[6] M.A. Lisa, S. Pratt, R. Soltz, U. Wiedemann, Ann. Rev. Nucl. Part. Sci. 55, 357 (2005).

[7] M. Gyulassy and S.S. Padula, Phys. Rev. C 41, R21 (1990); Phys. Lett. B 217, 181 (1989).

[8] J.P. Sullivan et al., Phys. Rev. Lett. 70, 3000 (1993).

[9] B.B. Back et al. (PHOBOS Collaboration), Phys. Rev. Lett. 85, 3100 (2000); Phys. Rev. Lett. 88, 022302 (2002).

[10] C. Adler et al. (STAR Collaboration), Phys. Rev. Lett. 87, 082301 (2001).

[11] S.C. Johnson et al. (PHENIX Collaboration), Nucl. Phys. A698, 603 (2002); W.A. Zajc et al., Nucl. Phys. A 698, 39 (2002).

[12] C. Greiner et al., Phys. Rev. Lett. 58, 1825 (1987); C. Spieles et al., Phys. Rev. Lett. 76, 1776 (1996).

[13] S. Soff et al., J. Phys. G 23, 2095 (1997); D. Ardouin et al., Phys. Lett. B 446, 191 (1999).

[14] G. Abbiendi et al. (OPAL Collaboration), Eur. J. Phys. C 21, 23 (2001).

[15] D. Buskulic et al. (ALEPH Collaboration), Z. Phys. C 64, 361 (1994).

[16] F. Antinori et al. (WA97 Collaboration), Nucl. Phys. A 661, 130c (1999).

[17] B. I. Abelev et al. (STAR Collaboration), Phys. Rev. C 74, 054902 (2006).

[18] J. Adams et al. (STAR Collaboration), Phys. Rev. Lett. 91, 262301 (2003).

[19] K. Morita, S. Muroya, and H. Nakamura, nucl-th/0310057.

[20] M. Csanád (PHENIX Collaboration), nucl-ex/0509042.

[21] R. Lednicky, nucl-th/0501065.

[22] R. Lednicky, V.V. Lyuboshits, and V.L. Lyuboshits, Phys. At. Nucl. 61, 2950 (1998).

[23] M. Gell-Mann and A. Pais, Phys. Rev. 97, 1387 (1955).

[24] V.L. Lyuboshitz, M.I. Podgoretsky, Sov. J. Nucl. Phys. 30, 407 (1979).

[25] G. Alexander and H.J. Lipkin, Phys. Lett. B 456, 270 (1999).

[26] G. Alexander, Rep. Prog. Phys. 66, 481 (2003).

[27] M. Gyulassy, Phys. Lett. B 286, 211 (1992).

[28] R. Lednicky and V.L. Lyuboshits, Sov. J. Nucl. Phys. 35, 770 (1982).

[29] B. Ananthanarayan, G. Colangelo, J. Gasser, and H. Leutwyler, Phys. Rept. 353, 207 (2001).

[30] A.D. Martin, E.N. Ozmutlu, and E.J. Squires, Nucl. Phys. B 121, 514 (1977).

[31] V. Baru et al., Eur. Phys. J. A 23, 523 (2005).

[32] A. Antonelli (KLOE Collaboration), hep-ex/0209069, eConf C020620 THAT06 (2002).

[33] N.N. Achasov, V.V. Gubin, Phys. Rev. D 63, 094007 (2001) for f₀, N.N. Achasov, A.N. Kiselev, Phys. Rev. D 68, 014006 (2003) for a₀.

[34] C. Adler et al. (STAR Collaboration), Phys. Lett. B 595, 143 (2004); S. Bekele, Ph.D. thesis, The Ohio State University, 2004 (http://www.star.bnl.gov/ central/publications/theses/2004).

[35] M. Anderson et al., Nucl. Instrum. Meth. A 499, 659 (2003); K.H. Ackerman et al. (STAR Collaboration), Nucl. Phys. A 661, 681c (1999).

[36] H. Wieman et al. (STAR Collaboration), IEEE Trans, Nucl. Sci. 44, 671 (1997); W. Betts et al. (STAR Collaboration), IEEE Trans, Nucl. Sci. 44, 592 (1997); S. Klein et al. (STAR Collaboration), IEEE Trans, Nucl. Sci. 43, 1768 (1996).

[37] C. Adler et al. (STAR Collaboration), Nucl. Instrum. Meth., A 461, 337 (2001).

[38] S. Eidelman et al., Review of Particle Physics (PDG), Phys. Lett. B 592, 1 (2004).

[39] J. Adams et al. (STAR Collaboration), Phys. Rev. C71, 044906 (2005).

[40] J. Adams et al. (STAR Collaboration), nucl-ex/0511003.

[41] U. Heinz, Nucl. Phys. A 610, 264 (1996).

Received on 13 December, 2006

Publication Dates

• Publication in this collection
  24 Sept 2007
• Date of issue
  Sept 2007

History

• Received
  13 Dec 2006