Surface-wave instabilities in a plasma rotating with step-like frequency profile

Surface-wave instabilities in a plasma rotating with step-like frequency profile

A.B. Mikhailovskii^I; V.D. Pustovitov^I; R.M.O. Galvão^II; C.H.S. Amador^III; J.G. Lominadze^IV; A.P. Churikov^V; O.A. Kharshiladze^VI

^IInstitute of Nuclear Fusion, Russian Research Centre Kurchatov Institute, 123182 Moscow, Russia

^IIBrazilian Center for Research in Physics, Rio de Janeiro, Brazil and Institute of Physics, University of São Paulo, São Paulo, Brazil

^IIIBrazilian Center for Research in Physics, Rio de Janeiro, Brazil

^IVKharadze Abastumani National Astrophysical Observatory, 0160 Tbilisi, Georgia and Nodia Institute of Geophysics, Tbilisi 0193 Tbilisi, Georgia

^VSyzran Branch of Samara Technical University, 446001 Syzran, Samara Region, Russia

^VINodia Institute of Geophysics, Tbilisi 0193 Tbilisi, Georgia

ABSTRACT

An approach for the theory of nonlocal magnetorotational and convective instabilities in a rotating plasma is developed, on the basis of the surface wave concept, which allows the derivation of useful analytical results.It is assumed that the rotation frequency has a step-like profile, so that a narrow transition layer separates two regions with different rotation frequencies. The one-fluid magnetohydrodynamic (MHD) model for description of the perturbed plasma dynamics is used. It is shown that in the case of magnetized plasma the main properties of the nonlocal (surface-wave) instabilities are similar to those of the local ones.

Keywords: Magnetorotational instability; Plasma rotational instability

1. INTRODUCTION AND OVERVIEW

One of the important issues in recent plasma physics studies is the spontaneous generation of magnetic field in a rotating plasma, motivated by numerous investigations of this effect in a rotating liquid metals (see pioneering papers [1-3] and the review [4]).

Because most of the previous analytical works in this field, starting with Ref. 1, were based upon a local-mode analysis, it is important to complement them with other theoretical approaches that allow for a simple description of non-local modes. In particular, the surface waves model, based upon step-like profiles of the equilibrium quantities, has been recently applied in a simplified analysis of the magnetorotational instability (MRI) [5]. One of the goals of the present work is to develop a more general theory of nonlocal modes in the surface-wave approximation.

First, let us define the model of simplest astrophysical equilibrium. This is a cylindrical plasma rotating in azimuthal direction θ with the angular frequency Ω = Ω(r), where r is the radius. The equilibrium magnetic field B₀ is assumed uniform and directed along the cylinder axis z, B₀ = (0,0,B₀). The model also includes a gravitational force g , with the radial component only, g = (g,0,0), and an equilibrium electric field E₀ = (E₀,0,0) related to the rotation frequency Ω = V₀/r by E₀ = -rΩB₀/c, where V₀ = V₀(r) is the azimuthal equilibrium plasma velocity and c is the speed of light. The equilibrium plasma pressure p₀ is assumed uniform, = 0, where prime is the radial derivative. Then the radial equilibrium condition yields

An alternative to the simplest astrophysical equilibrium is the simplest laboratory equilibrium. In this case g = 0, while ≠ 0. Then, instead of (1.1), one has

where ρ₀ is the equilibrium mass density.

A general case, when both g and are finite, can be called the astrophysical equilibrium with pressure gradient. Then, instead of (1.1) and (1.2), one has

The theory of nonlocal modes developed in Ref. 5 considered only the simplest astrophysical equilibrium, i.e., with = 0. In the present paper this theory is extended to equilibria with ≠ 0.

According to Ref. [1], with both g ≠ 0 and ≠ 0 two varieties of instabilities may appear: the MRI and the convective instability, CI. Our analysis includes both of them.

An important subset of the theory of local instabilities in a rotating plasma is the modes with parallel phase velocities much smaller than the sound velocity in a high-β plasma (the slow modes), where β is the ratio of plasma pressure to the magnetic field pressure. Here, althoug a complete analytical technique for arbitrary modes and arbitrary β is developed, we consider its applications primarily for slow modes in a high-β plasma.

One of the kee physics issues in this problem is the level of heat conductivity. In our analysis, preceded by Ref. [6] (see also Refs. [7, 8]), both cases of high and finite heat conductivity are considered.

The analysis of nonlocal perturbations requires a proper mode equation. Its derivation is presented in Sec. 2, which summarizes the mathematical technique developed for the case of high heat conductivity in Refs. [9, 10] (see also Refs. [11-14]) and for arbitrary heat conductivity in Refs. 15 and 16.

The main benchmarks of our technique are the pair of the canonical first-order differential equations for perturbations called the Hameiri-Bondeson-Iakono-Bhattacharjee (HBIB) type equations, first derived in [12, 13]. The variables in these equations are the perturbed radial magnetic field

_r, the so-called Friman-Rotenberg (FR) variable,

and

Here is the perturbed plasma pressure and 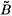_z is the parallel projection of the perturbed magnetic field. The mentioned canonical equations are

Here D, C₁,₁, C₂, and C₃ are the primary canonical parameters and k_z is the parallel wave number. We call the effect related to C₁ the first oblique effect, while that described by ₁ the second oblique effect. In [9, 10] it has been shown that the high heat conductivity leads to the following symmetry:

Below we prove that the same symmetry survives at arbitrary heat conductivity. This is important since in this case Eqs. (1.6) and (1.7) lead to a self-adjoint canonical mode equation

Here Λ is the secondary canonical parameter,

with a and b the secondary local and differential canonical parameters, respectively, determined by

In Sec. 3 we discuss the general aspects of the problem of slow modes in high-β plasma. There we use the so-called quasi-incompressible approximation, when the "sound propagator"

is replaced by

Here Γ is the adiabatic exponent, Δ_T is the characteristic heat-conductivity-induced decay rate, = ω - mΩ is the Doppler-shifted oscillation frequency with ω being the usual oscillation frequency and m the azimuthal mode number. Then the symmetry expressed by Eq. (1.8), describing the equality of the first and second oblique effects, is automatically satisfied.

As an alternative to the quasi-incompressible approximation, there is the Boussinesq approximation. We explain in Sec. 3 that the latter leads to

where the superscript "Bous" means Boussinesq. Then the first oblique effect disappears in the first canonical first-order differential equation, i.e., instead of (1.6), one has

We show in Sec. 3 that, instead of Eq. (1.7), the Boussinesq approximation yields the second canonical first-order equation of the form

where

Thereby, in the Boussinesq approximation one deals with nonvanishing second oblique effect, C₁≠ 0. Excluding p_* from Eq. (1.17) by means of Eq. (1.16), one arrives at the mode equation in the Boussinesq approximation

where

Comparing Eqs. (1.19) and Eq. (1.9), one can see that the Boussinesq approximation leads to a non-self-adjoint mode equation with reduced expression for Λ. Using the Boussinesq approximation, Ref. 6 has neglected the term with in Eq. (1.17). In this case the mode equation (1.19) is substituted by

Being central in the Balbus approximation this can be called the Balbus mode equation.

Section 4 is devoted to derivation of the nonlocal dispersion relation. In Sec. 5 the theory of nonlocal axisymmetric modes in the simplest astrophysical plasma is developed. In contrast, Sec. 6 considers the nonlocal axisymmetric modes allowing for both the gravitation force and the plasma pressure gradient. In Sec. 7 we transit to analysis of the nonaxisymmetric modes. Discussion of the results is given in Sec. 8.

It seems reasonable to compare the results of nonlocal and local theories. Our paper contains Appendices summarizing the local results obtained in [9, 15]: ^{Appendix A} shows the general preliminary results, while ^{Appendices B} and ^C are related to the axisymmetric and nonaxisymmetric modes, respectively.

2. BASIC EQUATIONS AND GENERAL TRANSFORMATIONS

2.1. Basic equations

We start with the standard MHD plasma motion equation

where V is the plasma velocity, B the magnetic field, p the plasma pressure, ρ is the plasma mass density, g is the gravitation force, and d/dt = ∂/ ∂t + V· ∇. We use the Ohm law in the form E + [V × B]/c = 0, where E is the electric field and c is the speed of light. This equation leads to the standard frozen-in condition

In addition, we use the Maxwell equation

the plasma continuity equation

and the heat conductivity equation

Here Γ = 5/3 is the adiabatic exponent, n = ρ/M is the plasma number density, M is the ion mass, T is the plasma temperature related to the pressure and density by p = nT, q is the heat flux defined by

where κ_T is the heat conductivity coefficient, b = B/B.

We consider a cylindrical plasma rotating in azimuthal direction θ with the angular frequency Ω = Ω(r) (r is the radius), which was described in Sec. 1 as the astrophysical equilibrium with pressure gradient, see Eq. (1.3). We linearize the basic equations assuming each perturbation to depend on t, θ, z as exp(-iωt + imθ + ik_zz), where ω is the oscillation frequency, m is the azimuthal mode number, k_z is the parallel projection of the wave vector. In addition to m, we introduce k_y ≡ m/r, the azimuthal projection of the wave vector, while, in addition to ω, we use the Doppler-shifted oscillation frequency = ω - mΩ. The (r,θ,z)-th projections of the perturbed plasma velocity are _r, _θ, and _z. 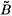Similarly, the (r,θ,z) components of the perturbed magnetic field are _r, 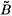_q, and 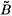_z. The perturbed plasma mass density is designated by .

The (r,θ)-th projections of the frozen-in condition (2.2) yield

The Maxwell equation (2.3) gives

The perturbed plasma motion equation (2.1) yields

Here is the Alfvén velocity squared, κ² = (2Ω/r)d(r²Ω)/dr, and the gravitation force is replaced through Ω and by means of Eq. (1.3).

With Eq. (2.9) we express

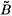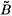_z in terms of _r, _θ:

where τ_B is given by Eq. (1.5).

With the FR variable p_* defined by Eq. (1.4) Eqs. (2.10) and (2.11) take the form

where .

It follows from Eq. (2.4), (2.7) and (2.9) that the perturbed density satisfies the equation

Now we linearize Eq. (2.5) obtaining [cf. (2.16)]

Here Δ_T is the characteristic heat-conductivity-induced decay rate given by At last, we have

2.2. Derivation of general canonical mode equation

2.2.1. Pair of canonical first-order differential equations

Substituting Eqs. (2.16) and (2.17) into Eq. (2.18), one has

It follows from Eqs. (2.12) and (2.19) that

Here is the "sound propagator" defined by Eq. (1.13). Substitution of Eq. (2.20) into Eqs. (2.19) and (2.16) yields

Substituting Eq. (1.4) into Eq. (2.14), we arrive at

Here

It follows from Eq. (2.15) that

Substitution of Eq. (2.27) into Eqs. (2.13) and (2.21) leads to

With Eqs. (2.28) and (2.29), Eq. (1.4) is represented in the form (1.6) where

Equation (1.6) is the first canonical first-order differential equation of the MHD approach. The effect described by the coefficient C₁ is the first oblique effect. It can be seen that this effect is revealed only if ≠ 0 or k_y ≠ 0.

Substitution of Eq. (2.27) into Eq. (2.23) yields

Using Eq. (1.6), we exclude τ_B from Eq. (2.33). Then we arrive at Eq. (1.7) where

By means of Eqs. (2.31) and (2.32), Eqs. (2.34) and (2.35) reduce to Eq. (1.8) and

Equation (1.7) is the second canonical first-order differential equation of the MHD approach. As a whole, Eqs. (1.7) and (1.8) are the Hameiri-Bondeson-Iakono-Bhattacharjee (HBIB) type equations. The effect described by the coefficient

₁ is the second oblique effect.

2.2.2. General canonical mode equation

In order to exclude the value p_* from our problem, we find from Eq. (1.7)

Then equation (1.8) takes the form of Eq. (1.9) with Λ given by Eqs. (1.10)-(1.12).

3. MODE EQUATIONS IN THE QUASI-INCOMPRESSIBLE, BOUSSINESQ, AND BALBUS APPROXIMATIONS

3.1. Quasi-incompressible approximation

We introduce the quasi-incompressible approximation assuming the parameter to be large but finite. Then the sound propagator given by Eq. (1.13) reduces to (1.14), which is relevant to the high-β plasma and the slow modes with parallel phase velocities much smaller than the sound velocity.

With Eq. (1.14), Eqs. (2.30)-(2.32), and (2.36) are transformed into

By means of the above expressions for C₁,C₂, and C₃, Eq. (1.11) reduces to

where

Similarly, Eq. (1.12) is transformed to

3.2. The Boussinesq approximation

By means of Eq. (2.4), one can exclude ∇ ·V from Eq. (2.5) arriving at the entropy equation

Neglecting the term dρ/dt in Eq. (2.4), one has the incompressibility condition

Using Eq. (3.10), instead of Eq. (2.4), together with Eq. (3.9), is the essence of the Boussinesq approximation.

In the case of axisymmetric perturbations Eq. (3.10) yields

Hence, using Eq. (2.7), one has

By means of Eq. (2.12) and (3.12), we arrive at

With Eq. (2.13) for k_y = 0 and (3.13), Eq. (1.4) leads to

This is the same as Eq. (1.6) for D and C₂ given by Eqs. (3.1) and (3.3) (for k_y = 0) and C₁ = 0, (see Eq. (1.15)).

Turning to Eq. (3.9), one finds

Substitution of Eq. (3.13) into (3.15) yields

It follows from Eq. (2.15) for k_y = 0 that

Substitution of Eq. (3.17) into Eq. (2.14) leads to

For given by Eq. (3.16) this equation means

where the constants D and C₃ are defined by Eqs. (3.1) and (3.4), respectively (for k_y = 0). Using Eq. (3.13), one can express τ_B in terms of p_* and arrive at an equation similar to Eq. (1.7), which is given by Eq. (1.17), where

Comparing Eq. (3.20) with Eq. (2.34) for k_y = 0 and using (1.14), one has (1.18). Then one arrives at the mode equation in the Boussinesq approximation given by (1.19), (1.20).

3.3. The Balbus approximation

In Ref. 6, the term with in Eq. (3.15) for has been neglected. This followed by the statement that such a neglect "is an implementation of the Boussinesq approximation (relative changes in the pressure are much smaller than relative changes in the temperature or density)". Then one arrives at the Balbus mode equation (1.21).

4. DERIVATION OF NONLOCAL DISPERSION RELATION

We represent (1.9) as

where

In the quasi-slab approximation, (4.1) reduces to

Assume that there is a jump of the rotation frequency Ω at r = r₀ from Ω₁ to Ω₂, where "1" means r < r₀ (the inside region) while "2" denotes r > r₀ (the outside region). The characteristic width of the transition layer between the regions is a r₀.

Far from the transition layer the functions G and H can by approximated by constants. Then solution of Eq. (4.4) decreasing with increasing |r - r₀| is given by

where is a constant and

Now we integrate Eq. (4.4) over a region of the width of order δ including the transition layer assuming a δ 1σ /_1,2 and 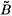r to be continuous. Then we obtain

where

Substitution of Eq. (4.5) into (4.7) leads to

This is the nonlocal dispersion relation.

In terms of the canonical parameters one has

where

The parameters C₁ and C₂ do not contain the δ-functional singularity. Then (4.11) reduces to

On the other hand, (4.10) is transformed to

The term I describes the nonlocal part of the nonlocal dispersion relation (4.9), while the local one.

According to Eqs. (3.1)-(3.4), in the case m = 0 (k_y = 0), = 0, i.e., in the case of slow axisymmetric modes in the simplest astrophysical plasma for low heat conductivity, one has

Then, starting from Eqs. (4.9), (4.12), and (4.13), we arrive at

where γ² = - ω².

5. SLOW AXISYMMETRIC MODES IN THE SIMPLEST ASTROPHYSICAL HIGH- β PLASMA

5.1. General properties of nonlocal modes

One can see that, since the two first terms on the right-hand side of Eq. (4.18) are positive, this equation can be satisfied only if

This condition shows that the instability is possible only for a decreasing profile of the rotation frequency, i.e., for dΩ²/d ln r < 0, which agrees with the results of [1-3].

5.2. The case of a magnetized plasma, γ k_zν_A

The perturbations described by (4.18) are marginally stable (γ = 0) for k_z = k_z0with

Turning to (B.5), one can see that, instead of (5.2), the local theory yields Eq. (B.6). It can be seen that (B.6) is in a qualitative agreement with (5.2).

Near the instability boundary, at Eq. (4.18) reduces to

At the same time, the expression for the squared growth rate near the instability boundary following from the local dispersion relation (B.5) is given by (B.8). One can see that there is a qualitative agreement between (B.8) and (5.3).

The instability condition following from (5.3) takes the form

or, in the explicit form,

One can see that, as for the local perturbations [1], sufficiently small wave number is necessary for the nonlocal instability. This agrees with the general results of [2, 3].

The above relations describe the nonlocal axisymmetric magnetorotational instability (MRI) in the simplest astrophysical high-β plasma, which is physically the same as the local MRI [1].

5.3. The case of nonmagnetized plasma

It follows from Eq. (4.18) for that

For γ ( Ω₂, Ω₁) one hence finds

Since we assumed r₀|k_z| 1, this equation should be considered for |Ω₁- Ω₂| Ω₁, when it turns into

In the opposite case γ (Ω₂, Ω₁) Eq. (5.6) yields

For γ ~ (Ω₂, Ω₁) one can take Ω₂ = Ω₁ = on the left-hand side of Eq. (5.6), where = ( Ω₁+ Ω₂)/2. Then (5.6) reduces to

This equation can be transformed into the bi-quadratic with respect to γ with the rule that Im ω > 0:

It hence follows that

where

The roots ω_2,3 are real, they are not of interest for the stability problem. The root ω₁ is generalization of Eqs. (5.8) and (5.9) for arbitrary Δ.

As a whole, the result of this subsection is compatible with the local solution mentioned in ^{Appendix B} .

6. SLOW NONLOCAL AXISYMMETRIC MODES IN A HIGH- β PLASMA WITH GRAVITATION FORCE AND PRESSURE GRADIENT

6.1. General dispersion relation for low heat conductivity

For axisymmetric modes, k_y = 0, Δ_T→ and ≠ 0, Eqs. (3.2)-(3.4) reduce to

Here is the squared sound velocity, Then Eq. (4.12) yields

Turning to (4.13) and using (6.1)-(6.3), we find

where

As a result, (4.9) reduces to

6.2. Slow modes in high- β plasma for low heat conductivity

It follows from (6.7) for β 1 and that

It is allowed here that for β 1 the jump in the pressure gradient is small as 1/β.

Taking here γ → 0, one arrives at the instability boundary [cf. (B.15)]

Turning to (B.11), Eq. (6.9) is represented as

where is defined by (B.11).

For > 0 this dispersion relation describes convective suppression of the nonlocal MRI. On the other hand, for

Eq. (6.10) describes the convective enhancement of this instability. In the case

the nonlocal MRI disappears and the nonlocal CI does not occur.

6.3. Slow modes in high- β plasma for high heat conductivity

According to [15], transition from the case of low to high heat conductivity is done by

in the final formulas. Then one arrives at the instability condition (6.10) with the substitution

where [cf. (B11)]

7. SLOW NONAXISYMMETRIC MODES IN THE SIMPLEST ASTROPHYSICAL HIGH- β PLASMA

In the case of uniform plasma pressure, = 0, one has by means of (4.12) and (4.13)

where

Then one should substitute (7.1) and (7.2) into the nonlocal dispersion relation (4.9).

For the slow modes in the case β → ∞ Eqs. (7.1) and (7.2) yield [5]

We restrict ourselves to the case of weak rotation frequency jump, so that

Then one can introduce the axilliary Doppler-shifted oscillation frequency

where

At the same time, in (7.5) we take for simplicity

We assume a small parameter and find it by the method of successive approximations. In terms of Eqs. (7.4) and (7.5) transit to

Using (4.9), (7.10), and (7.11), we obtain the dispersion relation [5]

where

Hence we find that the perturbations are unstable for

For k_y = 0 this instability condition reduces to (5.5). Comparing (7.14) with (5.5), one can see that the driving of the nonlocal nonaxisymmetric modes is weakened as compared with that of the axisymmetric modes. This conclusion is compatible with that for the local nonaxisymmetric modes discussed in ^{Appendix C}.

8. DISCUSSION

The first step to the equations describing the surface-wave instabilities is derivation of the MHD canonical mode equations. According to explanations of Sec. 1, our task is to derive expressions for the primary canonical parameters D, C₁, ₁, C₂, and C₃. In general form, these parameters are given by (2.30)-(2.32), (1.8) and (2.36). In the quasi-incompressible approximation, instead of these equations, one has (3.1)-(3.4).

Using our technique, we have analyzed applicability of the Boussinesq approximation for studying the slow modes in high-β plasma. Then we have found that this approximation leads to a non-self-adjoint equation (1.19). By this reason, it is, in general, unacceptable for such analysis. This drawback of the Boussinesq approximation can be eliminated by an artificial omitting of the term responsible for the non-self-adjointness. This has been done by Balbus in Ref. 6.

We have considered the surface-wave perturbations in the approximation of step-like equilibrium parameters. Then we have derived general nonlocal dispersion relation (4.9) with its local and nonlocal parts given by Eqs. (4.10) and (4.11), respectively. Reduced version of this dispersion relation for the case of slow axisymmetric modes in the simplest astrophysical plasma for low heat conductivity is given by Eq. (4.18). Analysis of Eq. (4.18) has lead to results presented in Sec. 5. Then we have shown that the nonlocal axisymmetric MRI, as the local one, is possible only for decreasing rotation frequency profile, see Eq. (5.1). The instability boundary is given by Eq. (5.2) showing that, as in the local case, only the perturbations with sufficiently small k_z can be unstable. The growth rate of the nonlocal MRI near its instability boundary is given by Eq. (5.3). The results of nonlocal and local theories show that the both varieties of the axisymmetric MRI must be similar.

With equilibrium pressure gradient, ≠ 0, in addition to the surface-wave MRI, the surface-wave convective instability can be revealed, see Sec. 6. In this case the situation with the surface-wave instabilities is similar to that mentioned in ^{Appendix B} for the local instabilities.

A more complicated picture is revealed for the nonlocal nonaxisymmetric MRI because of the radial dependence of the Doppler-shifted oscillation frequency . Dispersion relation of nonlocal nonaxisymmetric MRI is given by Eq. (4.9) with complementing Eqs. (7.4) and (7.5). Its instability criterion is given by Eq. (7.14). According to these equations, driving the nonlocal nonaxisymmetric MRI is hampered compared with that of the axisymmetric one.

Numerical calculations of nonlocal nonaxisymemtric MRI have been done in [17-21]. The analytical results presented here will be useful for understanding the results of computations and for further studies on both the nonaxisymemtric and axisymemtric MRIs.

Acknowledgments

We are grateful to A. I. Smolyakov, I. V. Khalzov and S. V. Vladimirov for valuable discussions. This work was supported in parts by the Russian Foundation of Basic Researches (RFBR), grant No. 06-02-16767, the Russian Program of Support of Leading Scientific Schools, grant # 9878.2006.2, the National Council of Science and Technology Development (CNPq), Brazil, the International Science and Technology Center (ISTC), grant # G-1217, and the Science and Technology Center in Ukraine, grant # 3473.

(Received on 26 November, 2008)

where

_r(r) is a slowly varying amplitude. Then (4.4) leads to

which is the local dispersion relation. The explicit form of this dispersion relation for low heat conductivity is

Here

where

while ξ^NA is defined by

The superscript "p" means a quantity dependent on the pressure gradient, while the superscript "NA" means "nonaxisymmetric".

Dispersion relation (A.3) for = 0 is represented in the form

Here , and

B.1. The simplest astrophysical plasma

For m = 0 Eq. (A.9) leads to the focal dispersion relation

For incompressible plasma with β 1, Eq. (B.1) reduces to

where The instability boundary is then given by

The growth rate near the instability boundary is defined by

Note also that for Eq. (B.2) has solution This solution describes the local instability for κ² < 0.

B.2. The local modes in the presence of pressure gradient

B.2.1. Local dispersion relation near instability boundary

For small ω and k_y = 0 one has from (A.3)

where

Then the dispersion relation (B.5) has the roots

One of these roots describes unstable modes for

Neglecting the term with in Eq. (B.6), one has

Then Eq. (B.9) is the Velikhov instability condition. The term with in Eq. (B.6) is responsible for the convective instability, CI. Following [1], one can introduce the Brunt-Väisälä (BV) frequency N_BV defined by

Then Eq. (B.6) is represented as

where

The BV effect is destabilizing for

With Eq. (B.6), the explicit form of the instability condition (B.9) is

This result coincides with that obtained in Ref. 1.

Taking to be a small parameter, we reduce (A.10) to

Then (A.9) is transformed to

For β → ∞ one has from (C.2)

where

the superscript "NA" means "nonaxisymmetric".

C.1.1. The approximation

/m → 0

Without the term with /m Eq. (C.3) reduces to

Then the instability boundary is given by

The nonaxisymmetric instability region corresponds to

At the same time, starting with (C.3), one can obtain that for the case of axisymmetric modes, k_y = 0, Eq. (C.6) is substituted by

where

Comparing (C.6) with (C.10), we conclude that the nonaxisymmetric perturbations are less dangerous than the axisymmetric ones.

• [1] S. A. Balbus and J. F. Hawley, Astrophys. J. 376, 214 (1991).
• [2] E. P. Velikhov, Sov. Phys. JETP 36, 995 (1959).
• [3] S. Chandrasekhar, Proc. Natl. Acad. Sci. USA 46, 253 (1960).
• [4] H. Ji, P. Kronberg, S. C. Prager, and D. A. Uzdensky, Phys. Plasmas 15, 058302 (2008).
• [5] A. B. Mikhailovskii, J. G. Lominadze, R. M. O. Galvão, A. P. Churikov, O. A. Kharshiladze, N. N. Erokhin, and C. H. S. Amador, Phys. Plasmas 15, 052109 (2008).
• [6] S. A. Balbus, Astrophys. J. 562, 909 (2001).
• [7] E. Quataert, Astrophys. J. 673, 758 (2008).
• [8] A. Socrates, I. J. Parrish, and J. M. Stone, Astrophys. J. 675, 357 (2008).
• [9] A. B. Mikhailovskii, J. G. Lominadze, A. P. Churikov, N. N. Erokhin, V. D. Pustovitov, and S. V. Konovalov, Axisymmetric magnetorotational instability in ideal and viscous plasma, Plasma Phys. Rep. 34, 837 (2008).
• [10] A. B. Mikhailovskii, J. G. Lominadze, R. M. O. Galvão, A. P. Churikov, N. N. Erokhin, A. I. Smolyakov, and V. S. Tsypin, Phys. Plasmas 15 052103 (2008).
• [11] E. Frieman and N. Rotenberg, Rev. Mod. Phys. 32, 898 (1960).
• [12] E. Hameiri, J. Math. Phys. 22, 2080 (1981).
• [13] A. Bondeson, R. Iacono and A. Bhattacharjee, Phys. Fluids 30, 2167 (1987).
• [14] R. Keppens, F. Casse and J. P. Goedbloed, Astrophys. J. 569, L121 (2002).
• [15] A. B. Mikhailovskii, J. G. Lominadze, A. I. Smolyakov, A. P. Churikov, V. D. Pustovitov, and O. A. Kharshiladze, Heat-conductivity-induced instabilities in a rotating plasma, Bul. Georg. Nat. Acad. Sci., to be published (2009).
• [16] A. B. Mikhailovskii, A. I. Smolyakov, J. G. Lominadze, A. P. Churikov, V. D. Pustovitov, and O. A. Kharshiladze, Effects of finite heat conductivity on instabilities in a rotating plasma, Plasma Phys. Rep. to be published (2009).
• [17] I. V. Khal'zov, V. I. Ilgisonis, A. I. Smolyakov, and E. P. Velikhov, Phys. Fluids 18, 124107 (2006).
• [18] L. L. Kitchatinov and G. Rudiger, Mon. Not. Roy, Astron. Soc. 286, 757 (1997).
• [19] G. Rudiger, L. Primavera, R. Arlt, and D. Elsner, Mon. Not. Roy Astron. Soc. 306, 913 (1999).
• [20] D. A. Shalybkov, G. Rudiger, and M. Shultz, Astron. Astrophys. 395, 339 (2002).
• [21] G. Rudiger, M. Shultz, and D. Shalybkov, Phys. Rev. E 67, 046312 (2003).

Appendix A  General results of the theory of local instabilities for low heat conductivity

Appendices B

Appendix C Local nonaxisymmetric modes in the simplest astrophysical plasma

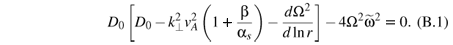
Publication Dates

• Publication in this collection
  16 June 2009
• Date of issue
  Mar 2009

History

• Received
  26 Nov 2008