The yield coefficient Yx/s was correlated with variables such as temperature (22.8-29.2 oC), concentrations of corn steep liquor (6.4-57.4 g/L), ammonium sulfate (5.6-18.4 g/L), sucrose (4.0-36.0 g/L) and soybean oil (3.0-7.0 g/L), all important variables in the growth stage of the Penicillium chrysogenum fungus. An empirical model was obtained by response surface statistical experimental design. The tests were performed with a complex culture medium in a rotatory shaker. The highest Yx/s values were obtained at low sucrose concentrations (~4.0 g/L) and high corn steep liquor concentrations (~57.4 g/L). Temperature, ammonium sulfate and soybean oil concentrations showed no significant effect on Yx/s
Penicillium chrysogenum; growth; yield; surface response
QUANTIFICATION OF THE EFFECT OF SOME OPERATIONAL VARIABLES ON THE CELL GROWTH YIELD (Y x/s ) OF Penilcilium chrysogenum BY SURFACE RESPONSE ANALYSIS
M.E.A.G. OPRIME and C.A.T. SUAZO 1
1Universidade Federal de São Carlos - Depto. de Engenharia Química
Via Washington Luiz, Km 235 Cx. Postal 676, CEP 13 565-905 - São Carlos, SP-Brazil
Fax: (016) 274-8266
(Received: June 11, 1997; Accepted: October 30, 1997)
Abstract - The yield coefficient Yx/s was correlated with variables such as temperature (22.8-29.2 oC), concentrations of corn steep liquor (6.4-57.4 g/L), ammonium sulfate (5.6-18.4 g/L), sucrose (4.0-36.0 g/L) and soybean oil (3.0-7.0 g/L), all important variables in the growth stage of the Penicillium chrysogenum fungus. An empirical model was obtained by response surface statistical experimental design. The tests were performed with a complex culture medium in a rotatory shaker. The highest Yx/s values were obtained at low sucrose concentrations (~4.0 g/L) and high corn steep liquor concentrations (~57.4 g/L). Temperature, ammonium sulfate and soybean oil concentrations showed no significant effect on Yx/s.
Keywords:Penicillium chrysogenum, growth, yield, surface response.
INTRODUCTION
Biotechnological processes are in general very complex, in virtue of the great number of variables involved. The process of penicillin production by the Penicillium chrysogenum filamentous fungus is a typical example of this complexity. The process basically comprises two steps: the rapid growth stage of the microorganism and the antibiotic production stage, in this case, a secondary metabolite. Both stages are interdependent, in such a way that abundant and quick cell growth is desirable for obtaining high productivity in the antibiotic biosynthesis. The efficiency at which the microorganism consumes the substrate, which is of great technological and economical interest, is defined as Yx/s. The choice of substrate, usually a carbohydrate, is important in this process, as this is a high cost raw material. According to Swartz (1979), the substrate represents about 11% of the total cost of the antibiotic.
Among the easily manipulated variables in industrial processes which strongly affect Yx/s of a specific strain are: the composition of the culture medium, the concentration of dissolved oxygen, the pH and the temperature. Attempts to optimize Yx/s have been limited to isolated studies of these variables, like those of Moyer and Coghill (1946), who demonstrated the great advantages of corn steep liquor as a nitrogen source; Jarvis and Johnson (1947), who selected alternative carbon and nitrogen sources; Pan et al. (1959), who investigated the use of fatty oils as an energy source; and Calam et al. (1951), who studied the effect of these variables on the integrated optimization. In practice, this type of investigation is quite complex because of the great number of tests required to correlate the variables. However, using statistical experimental design techniques may enable the obtainment of quick and reliable results.
The scope of this work was to study, with the aid of a statistical experimental design, the effect of some important variables in the growth stage of Penicillium chrysogenum on the yield coefficient Yx/s, aiming at the optimization of the biomass production.
MATERIALS AND METHODS
Microorganism: The microorganism used was Penicillium chrysogenum IFO 8644, a strain from the Institute for Fermentation-Osaka, Japan.
Sporulation medium: 7.5 g glycerol, 7.5 g glucose, 2.5 g corn steep liquor (CSL), 5.0 g peptone, 0.005 g MgSO4.7H2O, 0.06 g KH2PO4, 4.0 g NaCl, 20.0 g agar, 1 liter distilled water, pH = 6.0 ± 1 adjusted with ammonium.
Germination medium: 20.0 g sucrose, 30.0 g corn steep liquor, 7.0 g KH2PO4, 5.0 g (NH4)2SO4, 4.0 g MgSO4.7H2O, 5.0 g CaCO3, soybean oil 4.0 g, 20 mL salt solution, 1 liter tap water, pH = 6.0 ± 1 adjusted with NaOH.
Fermentation medium: 7.0 g KH2PO4, 4.0 g MgSO4.7H2O, 5.0 g CaCO3, 20 mL salt solution, 1 liter tap water, pH = 7.0 ± 1 adjusted with NaOH. Concentrations of sucrose, corn steep liquor, (NH4)2SO4, and soybean oil varied according to the experimental design (Table 1).
Salt solution: 3.0 g FeSO4.7H2O, 2.5 g CuSO4.7H2O, 10.0 g ZnSO4.7H2O, distilled water 1 liter.
Substrate concentration: Determination by the spectrophotometric method of Somogyi (1952), after acid hydrolysis of sucrose.
Cell concentration: Determination by dry mass in an oven at 105° C ± 1 for 24 hours.
EXPERIMENTAL
Germination: At this stage, three 500 mL Erlenmeyer flasks containing 100 mL germination medium were inoculated with a 10% suspension of spores. The flasks were placed in a rotatory shaker at 250 rpm and 26° C for 54 h.
Fermentation: At this stage, forty-five 250 mL Erlenmeyer flasks containing 60 mL of the fermentation medium were randomly inoculated with 10% inocula from the germination stage. Next, the flasks were placed in a shaker at 250 rpm for 24 hours. Samples of 15 mL each were taken at inoculation and after 24 hours of fermentation. Aftewards, the samples were centrifuged at 2200 rpm for 15 minutes for analysis of sugar in the supernatant and of cells in the precipitate.
Experimental design: Response surface analysis with two-level factorial design (-1 and +1) was employed for each variable; hence, the number of experiments carried out to investigate all possible combinations was equal to 2n, where n is the number of factors of interest. The independent variables chosen were temperature (x1), corn steep liquor concentration (x2), ammonium sulfate concentration (x3), sucrose concentration (x4), and soybean oil concentration (x5). The response variable measured was the cell yield Yx/s.
For the complete factorial design 2n , 32 experiments (tests 1 to 32) plus a triplicate of the central point (tests 33, 34 and 35) were carried out. Still, for the central compound design, the star configuration, 8 additional tests were conducted (tests 36-43), with a duplicate of the central point (tests 44 and 45). With the aid of a statistical software program, Statistical Analysis System (SAS), linear and second-order models, statistical refinement of the model, as well as variance analysis, were obtained.
The original and codified values attributed to the independent variables are listed in Table 1.
Codification of the variables was done by the by relationship (Myer, 1976):
where (1)
and
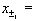 value of the variables in original units, fixed in the two-level factorial design (-1 and +1)
value of the variables in original units, fixed in the two-level factorial design (-1 and +1)
Theoretical background: Yx/s calculation
The cell yield coefficient Yx/s is defined as follows:
(2)
RESULTS AND DISCUSSION
The values obtained for the cell yield coefficient Yx/s and the experimental design matrix employed are listed in Table 2.
Linear Model for the Response Variable Y x/s
A linear regression was performed on the complete factorial design data (tests 1-35, Table 2), where a first-order model was obtained for the response variable Yx/s. The mathematical expression of the model is presented by equation (3):
(3)
Table 3 shows the results of the variance analysis for the linear model of Yx/s represented by equation (3).
In a table of F values (Box, et al., 1978), a value of 2.55 is encountered at a significance level of 5% associated with 5 (regression) and 29 (deviation) degrees of freedom. As can be seen in Table 3, the F value calculated is greater than the tabulated value; hence, the fitted model reasonably represents the Yx/s variable.
In Table 3, one can also observe that the quadratic terms are significant (F0.95; 1,.2= 18.51) at a significance level of 0.05, i.e., the region submitted to the experimental investigation is close to the surface curvature region, which can only be represented by a model of an order higher than one.
The data in Table 4, also show that the variable z5 (corresponding to the soybean concentration) was of little significance in obtaining the response variable Yx/s, as the probability of the parameter being equal to zero was shown to be very high in random conditions (41% probability). Therefore, this variable was assumed to be insignificant, i.e., of little importance. This variable was thus maintained at a constant value (4.0 g/L) while conducting the additional tests for the central compound design in order to test the second-order model for the response variable Yx/s.
Second-Order Model for the Response Variable Y x/s
In order to fit a second-order model, the initial factorial design was complemented with the tests corresponding to the central compound design (tests 36-43) and with the duplicate of the central point (tests 44 and 45). With the complete experimental design, the second-order model was then tested for the response variable Yx/s, whose mathematical expression is represented as follows:
(4)
In Table 5, it can be noted that the F value obtained (2.981) is greater than the tabulated value (2.75); hence, the fitted second-order model represents the Yx/s variable with a significance level of 1%.
Refinement of the Second-Order Model Obtained for the Response Variable Y x/s
In order to perform a graphical analysis of the response surface, the search for optimal values is only possible with two variables at the most. Hence, from Table 6, one may observe that factor z5 is the most significant, as it presents the highest F value (5.827) and a small degree of significance (0.07%). The next most significant variable is z2 with an F value (1.845) greater than that of the two remaining variables.
The second-order model can now be presented, considering only the most significant variables, as follows:
(5)
It can be observed that the F value obtained is greater than the tabulated F value; therefore, the reduced second-order model represented with great accuracy the experimental results, with a significance level of 0.1% (Table 7).
R2 = 0.3919
R2 = 0.5818
R2 = 0.4204
Figure 1: Quadratic surface referring to the 25 factorial design for the response variable Yx/s, with experimental points and boundary lines, for equation (5).
Figure 1 represents the second-order model obtained, where there is a region of minimum values for the response variable Yx/s. This is due to the functions quadratic term (5) regarding the sucrose variable (z42). Hence, upon positively or negatively incrementing values close to x4 = 20.0 g/L, the function minimum, the response variable Yx/s will increase (Figure 1). The temperature and ammonium sulfate concentration did not show any significant effect on Yx/s.
Within the experimental region, maximum yield values can be obtained for minimum x4 and maximum x2 values. Another aspect that should be taken into account is that through experimental data a mean value of Yx/s = 0.654 with a standard deviation of 0.179 was obtained. This value is equal to that encountered by Fonseca (1992) and greater than that encountered by Nagai (1986), who obtained a value of Yx/s = 0.43 when using glucose as the substrate. Righelato et al. (1968), working with a continuous culture of Penicillium chrysogenum, encountered a value of Yx/s = 0.45. An explanation for this difference is that the authors cited used synthetic medium, whereas Fonseca (1992) used a complex medium. Therefore, the medium containing corn steep liquor may have a source of carbon useful to Penicillium chrysogenum. Another possibility is that, according to information from the literature (Pan et al., 1959), the soybean oil added to the medium might have been used by the microorganism as an energy source, which might have caused an increase in the variation in cell mass (D x) and, consequently, an increase in Yx/s. It should also be taken into account that the strain used by Fonseca (1992) was the same as that used in this work and different from those used by Nagai (1986) and Righelato et al. (1968).
CONCLUSIONS
Analysis of the results by statistical parameters shows that for the variable cell yield coefficient (Yx/s), a second-order response surface is the one that best correlates the variables studied. Within the experimental region, it is recommended that in order to maximize the Yx/s values, cultivation of Penicillium chrysogenum should be conducted at low sucrose concentrations (~4.0 g/L) and high corn steep liquor concentrations (~57.4 g/L). The temperature, ammonium sulfate concentration and soybean oil concentration presented no significant effect on Yx/s.
NOMENCLATURE
Cso Concentration of the substrate at inoculation, g/L
Csf Concentration of the substrate at 24 hours of fermentation, g/L
Cxo Cell concentration at inoculation, g/L
Cxf Cell concentration at 24 hours of fermentation, g/L
H0 Test for the null hypothesis
R2 Determination coefficient
T Statistics of Students t distribution
xi Original variables
x1 Temperature, ° C
x2 Corn steep liquor concentration, g/L
x3 Ammonium sulfate concentration, g/L
x4 Sucrose concentration, g/L
x5 Soybean oil concentration, g/L
Yx/s Cell growth yield, g cell/g substrate
zi Codified variables
ACKNOWLEDGMENTS
The authors acknowledge the support received from CAPES in the form of a scholarship.
REFERENCES
Box, G.E.P.; Hunter, W.G. and Hunter, J.S., Statistics for Experimenters. New York, John Wiley & Sons, p. 655 (1978).
Calam, C.T.; Driver, N. and Bowers, F.H., Studies in the Production of Penicillin, Respiration and Growth of Penicillium chrysogenum in Submerged Culture, in Relation to Agitation and Oxygen Transfer. J. Appl. Chem., 1, pp. 209-216 (1951).
Fonseca, V.V., Influence of Agitation on Penicillin G in Stirred Tank Reactor, Masters thesis, Universidade Federal de São Carlos, São Carlos, Brazil, 95p. (1992).
Jarvis, F.G. and Johnson, M.J., The Role of the Constituents of Synthetic Media for Penicillin Production., J. Am. Chem. Soc., 69, pp. 3010-3017 (1947).
Moyer, A.J. and Coghill, R.D., Penicillin IX. The Laboratory Scale Production of Penicillin in Submerged Culture by Penicillium notatum Westling (NRRL 832), J. Bact., 51, pp. 79-83 (1946).
Myer, R.H., Response Surface Methodology. U.S.A., Library of Congress, p. 247 (1976).
Nagai, S., Metabolic Stoichiometry and Energetics. In: Bailey, J.E. and Ollis, D.F. Biochemical Engineering Fundamentals. 2d ed. New York: Mc Graw Hill, pp. 228-305 (1986).
Pan, S.C.; Bonaro, S. and Wagman, G.H., Efficient Utilization of Fatty Oils as Energy Source in Penicillin Fermentation. Applied Microbiol., 7, pp. 176-180 (1959).
Righelato, R.C.; Trinci, A.P.J.; Pirt, S.J. and Peat, A., The Influence of Maintenance Energy and Growth Rate on the Metabolic Activity, Morphology and Conidiation of P. chrysogenum. J. Gen. Microbiol., 50, pp. 399-412 (1968).
Somogyi, M., Notes on Sugar Determination. J. Biol. Chem., 195, pp. 19-23 (1952).
Swartz, R.W., The Use of Economic Analysis of Penicillin G Manufacturing Costs in Establishing Priorities for Fermentation Process Improvement. In: Perlman. D. (ed.) Annual Reports on Fermentation Processes, vol.3, Academic Press, New York, p.95 (1979).
References
- Calam, C.T.; Driver, N. and Bowers, F.H., Studies in the Production of Penicillin, Respiration and Growth of Penicillium chrysogenum in Submerged Culture, in Relation to Agitation and Oxygen Transfer. J. Appl. Chem., 1, pp. 209-216 (1951).
- Fonseca, V.V., Influence of Agitation on Penicillin G in Stirred Tank Reactor, Masters thesis, Universidade Federal de Săo Carlos, Săo Carlos, Brazil, 95p. (1992).
- Jarvis, F.G. and Johnson, M.J., The Role of the Constituents of Synthetic Media for Penicillin Production., J. Am. Chem. Soc., 69, pp. 3010-3017 (1947).
- Moyer, A.J. and Coghill, R.D., Penicillin IX. The Laboratory Scale Production of Penicillin in Submerged Culture by Penicillium notatum Westling (NRRL 832), J. Bact., 51, pp. 79-83 (1946).
- Myer, R.H., Response Surface Methodology. U.S.A., Library of Congress, p. 247 (1976).
- Nagai, S., Metabolic Stoichiometry and Energetics. In: Bailey, J.E. and Ollis, D.F. Biochemical Engineering Fundamentals. 2d ed. New York: Mc Graw Hill, pp. 228-305 (1986).
- Pan, S.C.; Bonaro, S. and Wagman, G.H., Efficient Utilization of Fatty Oils as Energy Source in Penicillin Fermentation. Applied Microbiol., 7, pp. 176-180 (1959).
- Righelato, R.C.; Trinci, A.P.J.; Pirt, S.J. and Peat, A., The Influence of Maintenance Energy and Growth Rate on the Metabolic Activity, Morphology and Conidiation of P. chrysogenum J. Gen. Microbiol., 50, pp. 399-412 (1968).
- Somogyi, M., Notes on Sugar Determination. J. Biol. Chem., 195, pp. 19-23 (1952).
- Swartz, R.W., The Use of Economic Analysis of Penicillin G Manufacturing Costs in Establishing Priorities for Fermentation Process Improvement. In: Perlman. D. (ed.) Annual Reports on Fermentation Processes, vol.3, Academic Press, New York, p.95 (1979).

 QUANTIFICATION OF THE EFFECT OF SOME OPERATIONAL VARIABLES ON THE CELL GROWTH YIELD (Yx/s) OF Penilcilium chrysogenum BY SURFACE RESPONSE ANALYSIS
QUANTIFICATION OF THE EFFECT OF SOME OPERATIONAL VARIABLES ON THE CELL GROWTH YIELD (Yx/s) OF Penilcilium chrysogenum BY SURFACE RESPONSE ANALYSIS




