Some alternating double sum formulae of multiple zeta values

Some alternating double sum formulae of multiple zeta values

Minking Eie^I; Fu-Yao Yang^II; Yao Lin Ong^III

^IDepartment of Mathematics, National Chung Cheng University, 168 University Rd. Minhsiung, Chiayi 62145, Taiwan

^IIDepartment of Information Management, Toko University, 51 University Rd. Sec. 2, Pu-Tzu, Chiayi 613, Taiwan

^IIIDepartment of Accounting and Information System, Chang Jung Christian University, Kway-Jen, Tainan 711, Taiwan. E-mails: [e-mail] / [e-mail] / [e-mail]

ABSTRACT

In this paper, we produce shuffle relations from multiple zeta values of the form ζ ({ 1 }^m-1, n+1). Here { 1 }^k is k repetitions of 1, and for a string of positive integers α₁, α₂, ...,α_r with α_r> 2 .

ζ (α₁, α₁, ..., α₁) =

Σ

n₁^–α1n₂^–α2... n_r^–αr

1 < n₁ < n₂ < ... < n_r

As applications of the sum formula and a newly developed weighted sum formula, we shall prove for even integers k, r > 0 that

k r Σ Σ (–1)^ℓ Σ ζ (α₀, α₁, ..., α_j + β_j, β_j+1, ..., β_k, β_k+1 + 1)

j = 0

ℓ = 0

|α| = j + r – ℓ + 1

|β| = k – j + ℓ + 2

+ Σ

Σ ζ (α₀, α₁, ..., α_kr – ℓ + 3) = ζ (k + r + 4).

0 < ℓ < r |α| = k + ℓ + 1

ℓ : even

Mathematical subject classification: Primary: 40A25, 40B05; Secondary: 11M99, 33E99.

Key words: multiple zeta values, sum formulae.

1 Introduction

For a pair of positive integers p and q with q > 2, the classical Euler sum S_{p, q} is defined as [2, 3, 8, 10]

The number p + q is the weight of S_p,q. When p = 1, or (p, q) = (2, 4), or (p, q) = (4, 2), or p = q, or p + q is odd, S_p,q can be expressed in terms of the special values of Riemann zeta function at positive integers. See [12, 13, 14] for the details of evaluations.

Multiple zeta values are multidimensional version of the Euler sums [1, 6, 9, 13, 14, 15]. For a string of positive integers α = (α₁, α₂, ..., α_r) with α_r> 2, the multiple zeta value or r-fold Euler sum ζ(α₁, α₂, ..., α_r) is defined as

or equivalently as

Here the numbers r and |α| = α₁ + α₂+ ... + α_r are the depth and the weight of ζ(α₁, α₂, ..., α_r), respectively.

For convenience, we let {1}^k be k repetitions of 1. For example,

ζ({1}³, 4) = ζ(1, 1, 1, 4) and ζ({1}⁴, 3) = ζ(1, 1, 1, 1, 3).

There is an integral representation, due to Kontsevich [4, 5, 13], to expressmultiple zeta values in terms of iterated integrals (or Drinfeld integrals) over simplices of weight-dimension, namely,

where

Ω_j = dt_j/(1 - t_j) if j ∈ {1, α₁ + 1, α₁ + α₂ + 1, ... , α₁ + ... + α_r-1 + 1}

and Ω_j = dt_j/t_j, otherwise. For our convenience, we rewrite the above integral representation as

An elementary consideration yields a depth-dimensional integral representation as

In particular, for positive integers m and n, we have

from which the so-called Drinfeld duality theorem

ζ({1}^m-1, n + 1) = ζ({1}^n-1, m + 1)

follows easily.

The above Drinfeld integral representation for multiple zeta values also enables us to express the product of two multiple zeta values as a linear combination of multiple zeta values through the shuffle product formula of two multiple zeta values. The shuffle product formula of two multiple zeta values is defined as

where the sum is taken over all permutations σ of the set { 1, 2, ..., m+n }, which preserve the orders of strings of differential forms Ω₁Ω₂...Ω_m and Ω_m+1Ω_m+2 ...Ω_m+n. More precisely, the permutation σ satisfies the condition

σ^-1(i) < σ^-1(j)

for all 1 < i < j < m and m+1 < i < j < m+n.

We restrict our attention to shuffle product formulae obtained from a group of multiple zeta values of the form ζ ({ 1 }^m-1, n+1) , which can be further expressed as integrals in one variable or double integrals in two variables. The following propositions are main tools for our exploration.

Proposition 1. [7] For a pair of positive integers m and n, we have

Proposition 2. [7] For an integer p > 0 and positive integers q, m and n with m > q, we have

In particular, for integers k, r > 0, one has

Proposition 3. [13] For positive integers a₁, b₁, a₂, b₂, ..., a_r, b_r, let

and p' be the dual of p,

Then for any integer ℓ> 0, we have

In this paper, we shall consider integrals of the form

which can be expressed as a finite sum of products of multiple zeta values of the form ζ({ 1 }^m-1, n+1). All possible interlacing of the variables t ₁,t ₂ and u₁,u₂ then produce 6 simplices. Integrations over each simplex give another expression in terms of 6 sums of multiple zeta values. Our alternating double sum of multiple zeta values is just one among them.

Theorem 4. For a pair of even integers k,r > 0, we have

Theorem 5. For a pair of even integers k,r > 0, we have

Some extensions of these theorems would be discussed in section 4.

2 Shuffle relations and the sum formula

In 1997, A. Granville proved the sum formula

which was originally conjectured independently by C. Moen and M. Schmidt around 1990 [11, 12, 13]. Also he mentioned that it was proved independently by Zagier in one of his unpublished papers. Here we show that the sum formula is equivalent to the evaluations of multiple zeta values of the form ζ({ 1 }^m-1, n+1).

Proposition 6. For a pair of integers k,r > 0, we have

In particular, when k+r is even

Proof. We begin with the integral

Rewriting the integrand of the above integral as

we see immediately the integral is separable, and by Proposition 1, its value is equal to

As a replacement of shuffle process, we decompose the region of integrationinto 6 simplices produced from all possible interlacing of variables t₁,t₂ and u₁,u₂. They are

(1) D₁: (t₁, t₂, u₁, u₂) ∈ [0, 1]⁴, 0 < t₁ < t₂ < u₁ < u₂ < 1,

(2) D₂: (t₁, t₂, u₁, u₂) ∈ [0, 1]⁴, 0 < u₁ < u₂ < t₁ < t₂ < 1,

(3) D₃: (t₁, t₂, u₁, u₂) ∈ [0, 1]⁴, 0 < t₁ < u₁ < t₂ < u₂ < 1,

(4) D₄: (t₁, t₂, u₁, u₂) ∈ [0, 1]⁴, 0 < t₁ < u₁ < u₂ < t₂ < 1,

(5) D₅: (t₁, t₂, u₁, u₂) ∈ [0, 1]⁴, 0 < u₁ < t₁ < t₂ < u₂ < 1 and

(6) D₆: (t₁, t₂, u₁, u₂) ∈ [0, 1]⁴, 0 < u₁ < t₁ < u₂ < t₂ < 1.

The integration over D₃, D₄, D₅ and D₆ are easily to get. For the simplex D₃:0 < t₁ < u₁ < t₂ < u₂ < 1, we rewrite the integral as

It comes from the Drinfeld integral

and hence its value is ζ ({ 1 }^k+1,r+3). A similar consideration leads to the values of the integrations over D₄, D₅ and D₆ are

(-1)^rζ({ 1 }^k+1,r+3), (-1)^kζ ({ 1 }^k+1,r+3) and (-1)^k+rζ ({ 1 }^k+1,r+3),

respectively.

For the simplex D₁:0 < t₁ < t₂ < u₁ < u₂ < 1, we substitute the factor

by

Consequently, in terms of multiple zeta values, the value of the integration over D₁ is

For 1 < j < k, we have

so that the sum in (2.1) is equal to

Identifying r-l+1 as a new dummy variable, the above sum is

Exchanging the roles of t₁,t₂ and u₁,u₂, the value of the integration over D₂ is

Adding all the values we get from the integrations over D₁,...,D₆, ourassertion follows.

□

Remark 7. When k+r is even, the sum formula

is equivalent to the evaluation

To obtain the relation when the weight is odd, we consider the integral

instead. Finally, we get the following relation

In particular, when k+r is even, we have

Note that the second sum of multiple zeta values is equal to

by Ohno's generalization of the sum formula and the duality theorem.

The following proposition plays an important role in our proof of Theorem 4 and 5.

Proposition 8. For a pair of integers k, r > 0 with k even, we have

Proof. Consider the integral

The above integral is separable and its value is given by

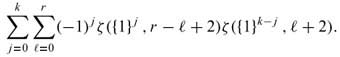
Let D_j(j = 1,2,3,4,5,6) be simplices obtained from all possible interlacing of variables t₁,t₂ and u₁,u₂. Note that the integrand of the integral is invariant if we exchange the roles of t₁,t₂ and u₁,u₂. Therefore, it suffices to evaluate the integration over D₁: 0 < t₁ < t₂ < u₁ < u₂ < 1, D₃:0 < t₁ < u₁ < t₂ < u₂ < 1 and D₄: 0 < t₁ < u₁ < u₂ < t₂ < 1.

For the simplex D₁, we rewrite the integral as

In terms of multiple zeta values, it is equal to

Sum over k leads to

Identifying r - l + 1 as a new variable α_k+1, it is

Both the integrations over D₃ and D₄ have the same value

(2^r+1-1) ζ({ 1 }^k+1, r+3).

Including the integrations over D₂, D₅ and D₆, we get the identity

Thus our assertion follows from the sum formula. □

3 The proof of Theorem 4

In our previous considerations, the integrands are so simple that it is easy to evaluate the integrations over all the simplices D_j (j = 1,2,3,4,5,6). It will be a different story for our next consideration. For our convenience, we shall use the notation

ζ(α,m) = ζ(α₀,α₁,...,α_k,m).

Now we are ready to prove Theorem 4.

Proof of Theorem 4. For a pair of integers k, r > 0, we consider the integral

Rewrite the second factor in the integrand as

Also we have

and

Consequently, the integral is separable and its value is given by

When both k and r are even, the above sum is equal to

The sum of the second summation, by Proposition 6, is equal to

and hence the total is

by Proposition 8.

Next we evaluate the integrations over D_j(j = 1,2,3,4,5,6). For the simplex D₁: 0 < t₁ < t₂ < u₁ < u₂ < 1, we rewrite the integral as

so it can be expressed as

or

For fixed l, by counting the number of ζ (α₀,α₁, ..., α_k,r - l +2) appeared in the summation, we conclude that the sum is equal to

Extending the above sum to l = -1 and then set l+1 as a new dummy variable, the sum is

The integration over D₂ is just the alternating double sum

which would be denoted by G in the after.

The integrations over D₃, D₄, D₅ and D₆ yield the following multiple zeta values

Adding together all the values obtained from the integrations over the simplices D_j (j = 1,2,3,4,5,6), we get the identity

Our assertion follows from

On the other hand, if we consider the integral

it has the value

The assertion in Theorem 5 follows after a similar procedure.

4 A final remark

Through the double generating function

we are able to express ζ ({ 1 }^m,n+2) in terms of the special values of Riemann zeta function at positive integers. The shuffle relations in Proposition 6 provide us to evaluate ζ({ 1 }^m,n+2) recursively in terms of special values of Riemann zeta function.

Another way to prove Theorem 4 is to count the number of appearances of each ζ(α₀,α₁,...,α_k,2) in the complicated double alternating sum. Therefore the identity is just a problem of counting and can be extended. For example, for a pair of even integers k,r > 0, we have

or for any positive integer m > 2,

or for a string of nonnegative integers p₀,p₁,...,p_k

All these identities are difficult to be proved otherwise.

Received: 26/III/09.

Accepted: 16/XII/09.

The third author was partially supported by Grant NSC99-2115-M-309-001 from the National Science Council of Taiwan, Republic of China.

• [1] T. Arakawa and M. Kaneko, Multiple zeta values, poly-Bernoulli numbers, and related zeta functions, Nagoya Math. J. 153 (1999), 189-209.
• [2] B. C. Berndt, Ramanujan's Notebooks, Part I and II, Spring-Verlag, New York, 1985, 1989.
• [3] J. M. Borwein and D. M. Bradley, Thirty-two Goldbach variations, Int. J. Number Theory 2(1) (2006), 65-103.
• [4] J. M. Borwein, D. M. Bradley, D. J. Broadhurst and P. Lisontex, Special values of multiple polylogarithms, Trans. Amer. Math. Soc. 353(3) (2000), 907-941.
• [5] D. Bowman and D. M. Bradley, Multiple polylogarithms: a brief survey, Contemp. Math. 291 (2001), 71-92.
• [6] M. Eie, W.-C. Liaw and Y. L. Ong, A restricted sum formula among multiple zeta values,J. Number Theory 129(4) (2009), 908-921.
• [7] M. Eie and C.-S. Wei, A short proof for the sum formula and its generalization, Arch. Math. 91(4) (2008), 330-338.
• [8] M. Eie and C.-S. Wei, New Euler sums with two branches, submitted (2008).
• [9] A. Granville, A decomposition of Riemann's zeta-function, Analytic number theory (Kyoto, 1996), 95-101.
• [10] M. E. Hoffman, Multiple harmonic series, Pacific J. Math. 152(2) (1992), 275-290.
• [11] M. E. Hoffman and C. Moen, Sums of triple harmonic series, J. Number Theory 60(2) (1996), 329-331.
• [12] C. Markett, Triple sums and the Riemann zeta function, J. Number Theory 48(2) (1994), 113-132.
• [13] Y. Ohno, A generalization of the duality and sum formulas on the multiple zeta values,J. Number Theory 74(1) (1999), 39-43.
• [14] Y. L. Ong, M. Eie and W.-C. Liaw, Explicit evaluations of triple Euler sums, Int. J. Number Theory 4(3) (2008), 437-451.
• [15] D. Zagier, Values of zeta functions and their applications, Progr. Math. 120 (1994), 497-512.

Publication Dates

• Publication in this collection
  22 Nov 2010
• Date of issue
  2010

History

• Accepted
  16 Dec 2009
• Received
  26 Mar 2009