Unstable planar one-dimensional configurations in nematic liquid crystals

Unstable Planar One-Dimensional Configurations in Nematic Liquid Crystals

M. Simões and A. E. Gonçalves

Departamento de Fisica, Universidade Estadual de Londrina

Campus Universitário, 86051-970, Londrina, PR, Brazil

Received on 23 November, 2001

In this work it is analytically shown that any one-dimensional non-uniform planar configuration is unstable with relation to out-of-plane tilts. The fluctuations describing this escape into the third dimension are studied, and it is shown that the minimization of the bulk free energy makes non-null the mean values of the parameters describing these uctuations. The equations describing this phenomenon are proposed and solved in the small bending approximation.

I Introduction

Usually, in the study of the textures and defects of the nematic liquid crystal (NLC), it is convenient to use a director planar configuration [1]. A typical example of such assumption is found in the study of magnetic walls [2], that make the transition between adjacent symmetrical distorted textures formed by the action of an external magnetic field. The director is initially prepared in such a way that, in the entire sample, it is uniformly aligned. Then, a constant magnetic field is applied perpendicularly to the initial director direction. As a result of the presence of this external field the nematic material presents a response that couples the bending of the director and the coherent motion of its micelles [3, 4, 5, 6]. The planar hypothesis assumes that, after this dynamic process the director is reoriented [5], but it remains in the plane delimited by its initial direction and the direction of the magnetic field.

The motivation for this assumption is clear. When a isolated magnetized rod is put in a magnetic field, with direction perpendicular to the rod's long axes, the rod becomes parallel to the external magnetic field turning around an axes of rotation that is always perpendicular to the plane formed by the initial orientation of the long axes of the rod, and the external magnetic field. Thus, as the nematic material is usually thought as an ensemble of rods, it would be expect that the director would always be achieved in the same initial plane, formed by the direction of the magnetic field and the initial direction of its long axes.

Nevertheless, such assumption has not an experimental evidence. It has been observed a lens effect in the light transmitted throughout a sample with magnetic walls [7, 8]. This effect was explained as result of a three-dimensional director deformation in which the planar configuration is lost and the director undergoes an out-of-plane deformation [9, 10]. This unsuspected behavior has a surprising explanation. The NLC matter cannot be thought as a simple collection of rods. Through the elastic forces the NLC micelles interact generating elastic tensions inside the sample. The resulting components of this induced stress make unstable any planar torsion of the director.

The most studied example of this out-of-plane tilt are the axial disclinations of the NLC [9, 10, 11]. For example, in order to study the disclination with S = 1 a planar configuration can be assumed [1, 11, 12]. When this is done the existence of a singular line, perpendicular to the plane of the texture, is predicted. But this prediction has not experimental support. It was found that the assumption of a planar configuration is the responsible for prediction of these singularities and it must be rejected because, in order to avoid the disclination line, the director "escapes into the third dimension" [10]. Likewise, for some others planar axial textures these disclinations lines are predicted and it has been found that the director can sometimes exhibits this turning to the third dimension and, in this way, it can eliminate the singularity in the nematic structure. Using as examples these axial textures, it could be believed that the escape into the third dimension is due to the reaction of the nematic material to the existence of the singular lines. In fact, it will be will shown here that this is not completely true. The turning to the third dimension results from the assumed textures at the planar configuration and it exists even when there is not singular lines in the bulk. This is the advantage of the one-dimensional textures; they present the planar instability without the need of these axial disclinations. Furthermore, these one-dimensional textures are important because they appear in samples subjected to external fields. Finally, some previous numerical calculations proposed to explain this escape to the third dimension (in the Fréedericks transition) reveal that such out-of-plane tilt would only occur above a critical field, greater than the Fréedericks threshold [7, 8]. We will demonstrate ahead that such critical field does not exist.

II Fundamentals

In this section the one-dimensional planar textures will be characterized, and the origin of its out-of-plane tilt will be studied. In order to accomplish this task let us consider the bulk free energy of a sample of nematic liquid crystal [1, 13]

where

K

₁₁,

K

₂₂, and

K

₃₃ are the elastic constants of splay, twist, and bend, respectively,

V is the volume of the sample, and

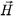
is an external magnetic field. A planar configuration will be understood as the one in which in all the sample the director field

(

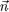
r) can be written as

q(

x,

y,

z) is the angle between the director and the

direction. Observe that the director component along the

direction is always null and, in all the sample, the director field can be described with only one parameter, the function q(

x,

y,

z). Suppose a nematic sample with dimension

a along the

x axis,

d along the

z axis, and infinitely long along the

y axis, and such that

a

d. Furthermore, the director is initially uniformly aligned along the

x axis, and an external controlled magnetic field

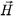
is applied along the

y axis, and strong boundary conditions are assumed at the sample edges. The energy

F

_p of this sample would be given by the substitution of Eq. (2) in it Eq. (1), which is

As we have said above, we will restrict this study to the so-called one-dimensional planar configurations. They are defined as the ones that, extending along the direction, do not change along the direction, that is

In the

Fig. 1 a photo of a magnetic wall illustrating this property is shown. Under this hypothesis the planar energy, Eq. (3), becomes

In order to work with a handleable expression, the two elastic constant approximation (K₁₁ = K₃₃) will be used (as we will see ahead this will not change our fundamental results). In this way, the free energy becomes [1, 2]

As we will investigate the planar stability of the structures resulting from the minimization of this free energy, we remember [14-22] that this geometry produces twist-bend walls in the sample [1, 15], whose the general solution satisfying the strong boundary conditions, is of the form

where 0 £

x £

a, 0 £

z £

d, and h(

x) gives the configuration of the nematic structure along the

x axis. The function sin(p

z/

d) describes the profile of the director along the

direction. In

Fig. 2 it is shown that at the edge of the sample (

z = 0 and

z =

d) the bending of the director is null, while at the center of the sample (

z =

d/2) it achieves its maximum value. The physical important issue about this profile is that along the

direction it is even with relation the plane

z =

d/2. As we will see ahead, this fact has important consequences in the geometry of the out-of-plane tilt. Furthermore, when sin

²q is expanded up to the fourth order term in q, as will be done below in Eq. (37), the function h(

x) giving a extreme of Eq. (6) through (7), results in a elliptic sine function (sn(

x,

k)) [23] of argument

k

where h₀ is the amplitude of oscillation of the wall, and k², 0 £ k²£ 1, gives the shape of the walls, and a = a(k) characterizes the periodicity of the wall. A profile of sn (x, k) is shown in Fig. 3. So, when the magnetic field is in the neighborhoods of the Fréedericks threshold (H » H_c), we have k » 0 and as k ® 0 we have sn (u, k) ® sinu. Also, as H ® ¥ we have k ® 1, and as k ® 1 we have sn(u, k) ®tanh u. Therefore, the walls' shape is a function of the magnetic field ( for details see [14]).

In the derivation of the above equation it has assumed that the walls are one-dimensional planar objects (It can be shown that its periodicity results from its one-dimensionality and vice-versa [17]). But it was not presented any argument that can justify this assumption. Furthermore, the derivation that we have presented is static. That is, it does not takes care of the internal motion of the nematic material. It was conjectured by Guyon et al. [3], and demonstrated by Lonberg et al. [5], that the elastic properties of the nematic medium are not enough to explain the observed walls geometry. The nematic material is an anisotropic liquid and, at the moment of the walls creation, its internal rearrangement must be taken in account. The director rotation stimulates the motion of the nematic material and it is this internal motion that gives rise to the one-dimensional (and periodic) character of the walls [17]. In fact, using the NLC anisotropic properties, it was shown that the observed geometry of the walls results from a coherent internal motion of the nematic material. That is, the external magnetic field creates an unstable situation that must be eliminated as fast as possible. This implies that the motion of the nematic material needs to occur with the smallest possible effective viscosity. In the search for the least effective viscosity the system selects the observed one-dimensional and the periodic geometry.

However, as soon as this motion ceases, the resulting one-dimensional walls' configuration is not found in a minimum of the elastic free energy, but in a local maximum. This fact leads to the fate of these structures: fluctuations arising at the nodes of the walls destroy their regularity leading then to closed elliptical structures [18]. An important issue about these fluctuations is that along their study it has been assumed that they are restricted to the plane of the walls, and perpendicular fluctuations have not been considered. Ahead, it will be shown that such out-of-plane fluctuations lead the director field to an escape into the third dimension. The correlation between this escape to the third dimension and the fate of the walls will not be considered here. Some reasons for this procedure will be given at the conclusion.

Observe that all this dynamical phenomenology, and the Fréedericksz transition, is induced by the linear term of the expansion determining the configuration given by Eq. (8). The higher order terms of this expansion determine the new stable configuration, but are not significant in the dynamical process giving the one-dimensional and periodic character of the walls. This observation will be important in the analysis of how the escape to the third dimension changes the planar configuration, to be given below in Eq. (42).

The approach to be developed below is not restricted to the magnetic walls, but is to be applied to every one-dimensional planar textures whose energy, and therefore the complete physical characterization, is given by the values of the parameters

at each point of the sample. If it is supposed that they are stable configurations, the fluctuations of the director in direction

, given by any one of the terms

must assume, in the mean, a null value. If a fluctuation induces a non-null value for some of these terms the corresponding planar configuration would be unstable. At the end of this work it will be shown that provided ¶

_xq and ¶

_zq are non-nulls the escape into the third dimension will always exist.

In order to implement this task the director's configuration will be described by the cylindrical coordinates

where

r =

r(

x,

y,

z) is the length of the projection of the director in the plane (

x,

y), and q(

x,

y,

z) is the angle between this projection and the

direction. In this parametrization a planar configuration, Eq. (2), would be obtained when

n

_z = 0, or

r

² = 1, everywhere. So, a non-null value of

n

_z would imply the existence of the out-of-plane tilt. Furthermore, observe that the relation fixing the director's length,

= 1, is trivially satisfied and, due to this relation, there are only two independent parameter fixing the director field. In this work we will use q and

n

_z. Observe that

r cannot be used, because it does not determine

n

_z uniquely. Nevertheless, we will continue to use, for convenience, the notation

n

_x,

n

_y,

n

_z, q and

r. But it cannot be forgot that these director's components aren't independent, but connected by the normalization of the director.

To obtain the equations driving the escape into the third dimension let us begin by rewriting the Frank free energy, Eq. (1), in the following form

where it was used the fact that

and

We make use of Eq. (4) and Eq. (11) and observe that

from which it follows that

and

Putting these results in the bulk free energy, Eq. (12), it is obtained

where

It is important to observe that in the first term, , n_x and n_y are connected to n_z through Eq. (13). Therefore, an out-of-plane tilt will change . Nevertheless, is the unique term in Eq. (18) that survives in the limit of the planar configuration. Furthermore, the remainder terms completely describe the dynamics of the parameters established in Eq. (10). So, they account for the escape into the third dimension through the iteration of n_z, or its variations, with the texture in the (x, y) plane. Consequently, it is only in this condition that the contributions of the terms of Eq. (10) will emerge.

III The origin of the out-of-plane tilt

In this section we will look for the origin of the forces that push the director to the third dimension. As it seems impossible to find an exact solution coupling all terms of Eq. (18) we will begin by showing that the one-dimensional planar configuration is unstable by assuming that all the elastic energy of the one-dimensional planar textures is contained in the term of Eq. (18). Our aim is to shown that, in order to relax the energy stored in , the director incline to the direction and others energy terms becomes non-null.

So, assuming that there is a one-dimensional planar configuration in the sample, let us consider the out-of-plane random fluctuations acting over it. As we have stated in Eq. (10), if the configuration is stable we must obtain án_zñ = 0, á¶_xn_zñ = 0, á¶_zn_zñ = 0, where án_zñ indicates the mean value of the random fluctuations of the variable n_z, and son on. In order to appreciate the development of each of these fluctuations we will assume that near the equilibrium the mean value is governed by the same laws of the corresponding macroscopic equilibrium variables, [25-28]. Therefore, the mean value of the variables described above could be calculated using the laws of motion giving the minimum of Eq. (18). Furthermore, we will suppose that these random fluctuations are independent and we will consider them separately. So, during the evaluation of a given term the mean value of the others ones will be supposed zero. As we will see immediately this hypothesis is untenable: at the end it results that the mean value of all these variables is non-null. This is a convenient contradiction: the only way to avoid it is to admit the existence of the out-of-plane tilt, just what we want to prove. In the next section the combined action of these terms will be studied.

To begin, consider

where

contains the energy of the textures in the (

x,

y) plane and

F

₃ contains the energy stored in the configuration

n

_z. As we have neglected the terms ¶

_z

n

_z and ¶

_x

n

_z the energy

F

₃ is analogous to a "potential energy" for

n

_z. By assuming that

will contain the main contribution to the energy of the observed textures, the term

F

₃ will be considered as a perturbation and we will neglected its influence on

. So, the minimum of

F

₃ is obtained for fluctuations of

n

_z around

Therefore, if ¶

_zq ¹ 0 and ¶

_xq ¹ 0, we obtain á

n

_zñ ¹ 0, and the planar configuration would be necessarily unstable. That is, only when ¶

_xq or ¶

_zq are null we would obtain á

n

_zñ = 0! As, according to Eq. (9) and Eq. (18), the planar texture is given by the values of ¶

_xq and ¶

_zq, the nullity of these parameters is equivalent to the absence of the planar texture. Furthermore,

n

_z would be proportional to ¶

_zq. This is an surprising result because, as we see in the Eq. (18), the q function is symmetric in relation to the plane given by

z =

d/2 and, therefore, ¶

_zq would be anti-symmetric with respect to this plane. Consequently, if in the upper half (

z >

d/2) of the sample the director tilts to the direction of increasing

z, in the lower half of this plane it would tilts to the direction of decreasing

z. Due the p symmetry of the nematic material (

is equivalent to -

), the major observable consequence of this anti-symmetry would be the fact that at the plane

z =

d/2 the out-of-plane tilt would be null.

Let us consider now the development of the mean value of the term á¶_zn_zñ. Its is given by

In exactly the same way that we have done to arrive at Eq. (27), if

K

₁₁¹ 0, we get

Finally we consider

and obtain

Observe that in these equations the term impelling the fluctuations of án_zñ, á¶_zn_zñ and á¶_xn_zñ is ¶_xq and ¶_zq. Therefore in order to obtain án_zñ = 0, á¶_zn_zñ = 0 and á¶_xn_zñ = 0 one must have ¶_xq = 0 and ¶_zq = 0. So, again, the existence of the non-null planar texture drives the out-of-plane tilt.

During the deduction of the Eqs. (26), (28) and (30) the mean value of each of the terms n_z, ¶_xn_z and ¶_zn_z has been supposed initially zero. This hypothesis has at least two advantages. Firstly, it gives a glimpse of the out-of-plane tilt by neglecting the interaction between these fluctuations and supposing that the are very close of the planar configuration. Secondly, it leads to a contradiction, because the final result is that these variables are not null. As said above the only way to avoid this contradiction in to assume the out-of-plane tilt.

IV A small bending solution

In the last section we have shown that the one-dimensional configuration gives a non-null value to the mean of each of the parameters of Eq. (18). But, our deduction does not consider the interaction between the parameters described by that equation. In order to take into account this interaction we will present an approximated analytic solution.

The escape into the third dimension will be considered as a weak phenomenon (of course this must be confirmed by our final results) that allow us to retain only its linear and quadratic terms (in n_z, ¶_zn_z, ¶_xn_z and their products). Furthermore, we will use the usual approximation K₁₁ = K₃₃, that produces an important simplification in without changing substantially the remainder terms of Eq. (18). Under these conditions we obtain

where

In the next step we observe that n_x and n_y, as defined in Eqs. (11), makes Eq. (31) highly non-linear. In order to consider this point we consider that

and that

In the following calculations only the term of fourth order in q and its derivatives (or products between both) will be retained. Furthermore, we recall that

r

²=1-

n

_z

² and use in advance the result of Eq. (43), that shows that

n

_z is quadratic in q and its derivatives. Therefore, by keeping the forth order term in q we are being consistent with the small bending approximation used in Eq. (32) to Eq. (35). With these approximations we have

Now the Euler-Lagrange equation for q is

and the equation for

n

_z is

As observed above, Eq. (43) shows that n_z is of second order in q. Therefore, the change in the planar texture due to the out-of-plane tilt, given in Eq. (42) is of third order in q. Moreover, we remember that the bending of the director at the Fréedericksz threshold, and the dynamic instability resulting from it, is driven by the first order term of this equation [1]. The function of third order term is to stabilize the new least energy configuration, and it will not change the fundamental walls' characteristics: one-dimensionality and periodicity. So, a suitable, and usual [5, 7], approximation for the solution of Eq. (42) is given by

Of course sin(2p

x/l) is an approximation to the sn(a

x,

k) , given in Eq. (8) and

Fig. 3, that preserves its fundamental property: periodicity. As can be easily verified, when Eq. (44) is substituted in Eq. (43), the solution for

n

_z becomes

From this equation we see that, according to the approximation that we are using, the out-of-plane tilt only exists if K₃₃¹ K₂₂. Furthermore, it is really anti-symmetric with relation to the plane z=d/2. In the Fig. 4 it is shown a profile along the direction of the director given by Eq. (7), or (44), and the predicted out-of-plane tilt given by the above equation. Another important result is that the out-of-plane tilt is proportional to d/l. This means that, with the use of samples for which d << l, it would be a very small effect. Finally, observe that along the direction the phenomenon is null exactly at the walls' nodes and at points where the walls achieve their maximum bending.

V Final remarks and conclusion

We have considered the origin of the out-of-plane tilt by studying the trends of the fluctuations of án_zñ, á¶_zn_zñ and á¶_xn_zñ. But, it is widely known that in the magnetic walls there are important in-plane fluctuations and, it is believed, these fluctuations are the responsible for the fate of the walls [18]. From this picture, and considering the results exposed along this paper, it can be asked: is the established picture - of the instability of the walls - changed by the out-of-plane fluctuations? Without a doubt, some further efforts must be done in this problem, but it seems that these two kinds of fluctuations have completely different roles in the physics of the magnetic walls. In a previous work, it has been shown how the fate of the walls is drove by large in-plane fluctuations happening at the places where, even in the presence of the external magnetic field, the director does not bend at all. These places form the nodes of the walls. But, Fig. 5 shows that just at the nodes of the walls the out-of-plane tilt is zero. Therefore it seems that the two kinds of fluctuations have its action at different places of the walls, and its interaction could be neglected. Furthermore, to find an approximated solution, we used a small bending approach where the planar configuration has been considered as the predominant energy term.

As a final remark, we remember that in a previous numerical study it has been predicted that the out-of-plane tilt would only occur above a critical point [7, 8]. In our analytical study we have not found it. We believe that this difference comes from the fact that in that numerical study it has been assumed an even function, with relation to z = d/2, for the out-of-plane tilt and, as we have anticipated in Eq. (26) and deduced in Eq. (45), this is indeed and odd function.

Acknowledgments

This work was supported by the Brazilian agencies CNPq and Araucária.

• [1] P.G. de Gennes, The Physics of Liquid Crystals, Clarendon Press, Oxford, 2nd edition, 1993.
• [2] F. Brochard , J. Phys. (Paris), 33, 607 (1972).
• [3] E. Guyon, R. Meyer, and J. Salan. Mol. Cryst. Liq. Cryst. 54, 261 (1979).
• [4] J. Charvolin, and Y. Hendrix, J. Phys. (Paris) Lett. 41, 597 (1980).
• [5] F. Lonberg, S. Fraden, A.J. Hurd, and R.B. Meyer, Phys. Rev. Lett. 52, 1903 (1984).
• [6] G. Srajer, S. Fraden, and R. Meyer, Phys. Rev. A 39,9 4828(1989).
• [7] M. Grigutsch, N. Klöpper, H. Schmiedel, and R. Stannarius, Mol. Cryst. Liq. Cryst. 261, 283-292 (1995).
• [8] M. Grigutsch, N. Klöpper, H. Schmiedel, and R. Stannarius, Phys. Rev. E 49, 5452 (1994).
• [9] P.E. Cladis , M. Kléman, J. de Physique 33, 591 (1972).
• [10] R.B. Meyer, Phyl. Mag. 27, 405 (1973).
• [11] M. Kléman, Defects in Liquid Crystals, in Advances in Liquid Crystals. Edited by Glenn H. Brown, Academic Press, New York 1975.
• [12] G. Vertogen, W. H. de Jeu, Thermotropic Liquid Crystals, Fundamentals Springer-Verlag, Berlin, Heidelberg, 1988.
• [13] F.C. Frank, Discussions Faraday Soc. 25, 19 (1958).
• [14] A.J. Palangana, M. Simões, L.R. Evangelista, and A. A. Arroteia, Phys. Rev. E 56, 4282 (1997).
• [15] M. Simões, A.J. Palangana, and L.R. Evangelista, Phys. Rev. E 54, 3765 (1996).
• [16] M. Simões, Phys. Rev. E 54, 6952 (1996).
• [17] M. Simões, Phys. Rev. E 56, 3061 (1997).
• [18] M. Simões, A. J. Palangana, and F.C. Cardoso, Phys. Rev. E 58, 323 (1998).
• [19] M. Simões, A. J. Palangana, and L.R. Evangelista, Phys. Rev. E 56, 7326 (1997).
• [20] M. Simões and A.A. Arrotéia, Phys. Rev. E 59, 556 (1999).
• [21] P.A. Santoro, A.J. Palangana, and M. Simões, Phys. Lett. A 243, 71 (1998).
• [22] M. Simões, A.J. Palangana, and L.R. Evangelista, Braz. J. Phys. 28, 348 (1998).
• [23] P.F. Byrd and M.D. Friedman, Handbook of Elliptic Integrals for Engineers and Physicists, (Springer-Verlag, Berlin, 1954).
• [24] W.H. de Jeu, Physical properties of liquid crystalline materials, (Gordon and Breach, Science Publishers, 1979).
• [25] L. Onsager, Phys. Rev. 37, 405 (1931).
• [26] L. Onsager, Phys. Rev. 38, 2265(1931).
• [27] D. Chandler,  Introduction to modern statistical mechanics,(Oxford University Press, New York, 1987) Chap. 8.
• [28] Hydrodynamic Fluctuations, Broken Symmetry, and Correlation Functions Frontiers in Physics. The Benjamin/Cummings Publishing Company, INC. 1975.

Publication Dates

• Publication in this collection
  20 Nov 2002
• Date of issue
  June 2002

History

• Received
  23 Nov 2001