Population, growth and health expenditure

Population, growth and health expenditure^*

Luis Currais

Department of Economic Analysis, Faculty of Economics, La Coruña University (e-mail: [e-mail])

Summary: 1. Introduction; 2. Some previous results; 3. Setup of the model; 4. Transitional dynamics and the steady-state analysis; 5. Conclusions.

A genuine understanding of the economic growth process should take into account the extent to which fertility and mortality affect the population growth rate as an endogenous variable. To this end we construct a growth model using an infinite horizon setup in which economic development and health status influence the population growth rate. Mortality depends on health expenditure, and fertility is endogenously determined. Adults within each household take into account the welfare and resources of their current and future descendants. Their decisions determine not only the evolution of the population growth rate but also the evolution of the per capita income.

Key words: fertility; mortality; growth; health expenditure.

JEL Codes: J13, I12, O47 and H51.

RESUMO

Este artigo analisa a mortalidade e a fertilidade como variáveis endógenas ao modelo e determinantes do crescimento da população associado ao processo de crescimento econômico. Com este propósito, é desenvolvido um modelo de horizonte infinito onde tanto o nível de desenvolvimento econômico quanto o gasto em saúde influenciam a taxa de crescimento da população. Cada família toma suas decisões tendo em conta o bem-estar social e os recursos disponíveis de seus descendentes atuais e futuros. Suas decisões determinam não só a evolução da taxa de crescimento da população, mas também a evolução da renda per capita.

1. Introduction

The effects of economic factors on fertility and mortality were a central element in development for Malthus (1986) in 1798. Other economists such as Adam Smith (1937), Schumpeter (1954) and David Hume (Rostow, 1990) also discussed the connection between population and subsistence resources. According to their predictions, rising prosperity would yield a greater increase in population growth until a food supply limit was reached. Although the findings of empirical studies do not support the ''Malthusian paradigm'' (Shultz, 1985; Coale, 1986; Rostow, 1990; Kremer, 1993), its impact meant that population began to be treated as an endogenous element derived from economic and social conditions.

The neoclassical models of Solow (1956), Cass (1965) and Koopmans (1965) consider the population growth exogenous and thus neglect interactions between the economic growth process and demographic trends. These models are unable to capture the observable diversity of population growth through the variance in the behavior of fertility and mortality rates among different countries. We might make a similar observation for a single economy over time and about the development process.

In order to better understand the economic growth process we should take into account the extent to which fertility or longevity affects the population growth rate as an endogenous variable. To this end we construct a growth model using an infinite horizon setup in which economic development and health status influence the population growth rate through their implications on fertility and mortality rates.

This paper is organized into five sections. In the following section we briefly discuss previous results obtained by different authors. In section 3 we present an infinite horizon model in which economic development and health status influence the population growth rate through their impact on fertility and mortality rates. Section 4 analyzes the transitional dynamics and the steady state properties of the model. Our concluding remarks are given in the last section.

2. Some Previous Results

Several authors have studied the feedback between population growth and development. These studies follow the work of Becker (1960), which analyzes the behavior of demographic and economic changes in developed countries and the role of fertility.

Endogenous population growth literature has progressed along two basic research lines. On the one hand, we find those studies that follow the neoclassical growth model, where the economic growth rate is exogenously determined. The analysis of population growth as an endogenous variable, along with the analysis of several economic factors in different static and dynamic environments, yields distinct results in which the quantity and quality of children have an important role in the economy (Becker & Lewis, 1973; Barro & Sala, 1995). Other factors which act as incentives to have children, such as intergenerational transfers (Cadwell, 1976 and 1982; Willis, 1989), the effects of the social security system (Nugent, 1985; Entwistle & Winegarden, 1984) and different approaches to child rearing costs (Eckstein & Wolpin, 1985), are also analyzed in different models. On the other hand, we find several studies based on models where economic growth and population growth rates are endogenous and simultaneously determined as a result of distinct initial conditions or changes in the parameters of the model that yield economic growth (Becker, Murphy & Tamura, 1990; Ehrlich, 1991).

The relationships between human capital and health economics theories, and their consequences for longevity and fertility, are directly linked to ''modern'' endogenous population growth literature (Grossman, 1972; Ehrlich & Chuma, 1990). Becker, Murphy and Tamura (1990), Becker (1991), and Barro and Sala (1995) stress the connection between human capital and the costs of child rearing. Becker and Barro (1988) develop a model where fertility is endogenously determined and depends on per capita quantities of human and physical capital.

According to the World Bank (1993), falls in mortality and morbidity rates, which are linked to per capita health expenditure, and their consequences for a healthier population and work force are important in promoting economic productivity and fomenting economic development. Barro and Sala (1995:432) analyze the effects of health on economic growth. In their study of the determinants of growth they find that life expectancy, as a proxy for health, is an important factor for growth: a 13 year increase in life expectancy is estimated to provoke an increase in the annual growth rate by 1.4 percentage points. Jablonski, Rosemblum and Kunze (1988) carry out a study of the relationship between life expectancy, productivity and health and obtain similar empirical conclusions in terms of life expectancy. These results are supported by the theoretical and empirical findings of Currais and Rivera (1999a, 1999b). In their model, health expenditure, used as a proxy for health status, increases productivity through its effect on human capital accumulation.

3. Setup of the Model

This model is an extension to the fertility choice model of Becker and Barro (1988) and the continuous time approach proposed by Barro and Sala (1995). We consider an infinite horizon model where mortality depends on health expenditure and fertility is endogenously determined. Thus, each generation of the family is linked altruistically and adults within each household take into account the welfare and resources of their current and future descendants. The current generation maximizes utility and incorporates a budget constraint over an infinite horizon. We consider that altruistic parents provide transfers to their children, who also consider in turn their transfers to their children, and so on.

Time is continuos and there is a large number of firms in the market that act competitively. Each firm hires labor L and rent capital K in competitive factor markets and sells its products in a competitive goods market. Firms take the technological progress A as given, and it grows at the rate x. They maximize their profits, which are owned by households; thus, households accrue profits.

At each point in time firms employ the stocks of labor L and capital K, paying for their marginal products and selling the produced output. Each firm produces a flow of output Y according to Y = F(K,AL). The production function represents a labor-augmenting technological progress that occurs at the constant rate x > 0. In the Cobb-Douglas case we obtain that = ^a, where 0 < a < 1, and = ye^–xt and = ke^–xt represent respectively per capita income and per capita capital in terms of effective labor. Capital depreciates at the constant rate d and firms pay the marginal product of factors r = aAa–1-d and w = (1-a)A

^ae^xt.

The economy has a large number of identical households that seek to maximize utility. Their preferences are described by the intertemporal utility function:

where r is the rate of time preference and represents parental altruism, which corresponds to r > 0, N is the size of a typical dynasty, n and d are the family's fertility and mortality rates respectively, and c is the consumption of each member of the household. As the exogenous growth rate of technological progress occurs at a constant rate x, so that = ge^–xt is the per capita health expenditure in terms of effective labor, here d() is the family's mortality rate that depends on per capita health expenditure in terms of effective labor.

The use of the mortality rate as a function of health expenditure per efficiency unit of labor seeks to capture the effects highlighted by some empirical studies. Newhouse (1977) argues that the marginal unit of health care may contribute more to ''caring'' (or subjective components of health) than to ''curing'' (or physiological health). This result supports the conclusions of several studies using data on mortality and morbidity. According to Parkin et alii (1987), it is equally plausible to assume that the marginal unit of medical care does produce an improvement in physiological health, but that the cost of this marginal unit is greater for higher income/higher expenditure countries. In this sense as cheaper diseases are eradicated by increased expenditure, more expensive diseases take their place.

By assumption, we take the function d() as a C² function verifying that d() > 0, d¢() < 0 and d¢¢() > 0, "> 0. In other words, the mortality rate decreases as increases, but the greater the expenditure the smaller its decrease. Some other desirable features might be that d(0) > 0. This means that with no health expenditure the mortality rate would be the ''natural'' mortality rate. Another desirable feature is that d() = , with 0 < < d(0). This fact could be justified since health gains are effectively bounded. It signifies that under no circumstances the mortality rate falls below . The size of the family changes continuously according to

The way that this model is developed means that one should interpret d as representing infant mortality, thus n-d is understood to be the number of surviving children. It is possible to interpret the analysis more generally by thinking in terms of a broad concept of death, since mortality rates at all ages are likely to depend on some basic common factors.¹ Households are competitive, thus each of them takes as given the interest rate r and receives the same wage rate w per unit of labor services. Each adult supplies inelastically one unit of labor per unit of time. The family's assets k, considering the case of a close economy, earn the rate of return r.

We can also introduce the same relationship, proposed by different authors, between the individual per capita quantity of capital k and the cost of child rearing F. The cost of child rearing F would tend to increase with parents income or with other measures of the opportunity costs of parental time. We use instead a simplified linear function of child rearing costs, as follows:

where bk represents the opportunity costs that increase with parental capital intensity.²

The total per capita income received by each household is the sum of wages and interest income. Thus, the family's budget constraint can be expressed as:

where w is the wage rate and r is the interest rate.

The household optimization problem lies in maximizing (1), subject to (2) and (3). Solving the model by using optimal control (see ^appendix), we obtain the following expressions:

4. Transitional Dynamics and the Steady-State Analysis

The stability of the equilibrium can be studied making a linear approximation to (4) around the steady state. To simplify the work, we can eliminate by using (19.A), and expressing (4) in terms of and as

Working with instead of is not an inconvenient, since the relationship between and is one-to-one according to (19.A).

Now let us make some assumptions about the function d() and the parameters of the model. First, we assume that the mortality rate is related to health expenditure through a negative exponential function:

In order for d to be a decreasing function, T < 0. This function verifies all the desirable features for the mortality rate pointed out in the assumptions of the model. The natural mortality rate (in the absence of health expenditure) is L+M, and the threshold value below which the mortality rate may not go is L. The parameter S is related to the decrease rate of the mortality rate. We consider the following benchmark taking into account the common parameters used in Barro and Sala (1995):

The stability of equilibrium can be ascertained determining the Jacobian matrix of (5) in the steady state. We can express the Jacobian matrix of and in the steady state as

whose eigenvalues are

₁ = 0.0454243 and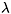 ₂ = -0.0254243, with associated eigenvectors respectively of (0.879683, -0.47556) and (-0.997771, -0.0667253). Hence, the model exhibits saddle-path stability.

Examining the Jacobian matrix, we see that the = 0 locus is negatively sloped and stable, since declines for for a given . The = 0 locus is positively sloped around the steady state, but is unstable since rises for for a given . As the model exhibits saddle-path stability, there is only one stable trajectory. We calculate the policy function () for the stable arm by using the time elimination method of Mulligan and Sala (1993). The transitional path and the phase diagram are presented in figure 1. The relationship between and along the locus = 0 is the solution to a quadratic equation which has two real positive roots for a range of reasonable parameters (see ^appendix). The larger root always turns out to lie above the = 0. Thus, in figure 1 we only represent the smaller root of = 0. The figure shows that the transitional path is positively sloped. Hence, if the economy starts from a state of low initial per capita capital, one which is below its steady-state value and where per capita health expenditure is low, capital and per capita health expenditure grow along the transition path towards the steady state.

Figure 2 shows that the fertility rate exhibits a monotonic behavior. It decreases towards its stationary value as the economy develops. The fertility and mortality rates are correlated in a significant and negative way with the per capita income. As the economy develops, the fertility and the mortality rates fall and are accompanied by an increase in per capita income. This behavior characterizes the so-called ''modern growth regime'' that the economy undergoes after the demographic transition (Rostow, 1990; Maddison, 1985). Reduced mortality levels and a healthier population are major contributors to a rise in living standards, which is often regarded as a major factor in fertility decline. Figure 3 shows the evolution of the mortality rate.

Table 1 presents the effect on the steady-state values of the variables , , , d, n, and r on changing the designated parameter, remaining all others in their baseline settings.

Changes in y and f lead to changes of n and d in the same direction. That is an expected result, since the higher the value for y or f, the greater the benefits in terms of utility with respect to the children. For instance, when y rises from its baseline value to 0.3, the mortality rate increases from 0.0089 to 0.009285, and the fertility rate thus changes from 0.0155 to 0.0173. The variation in the fertility rate is greater than the variation in the mortality rate, reflecting the effect of the rising in c/k from 0.0497 to 0.0502. Hence, the net rate of population growth also rises from 0.00662 to 0.00807.

We note a similar pattern when f increases to 0.3, although this effect is stronger than that provoked by y on n and d. For example, n rises to 0.0202 and d rises to 0.0099, which gives a net rate of population growth of 0.0103. A variation in b yields a change in the fertility rate in the opposite direction, reflecting the importance of the child rearing cost. For example, as b rises from 0.5 to 2, the fertility rate declines from 0.022 to 0.0113. Furthermore, the mortality rate declines from 0.01161 to 0.00752 due to an increase in health expenditure. Since health expenditure is aimed at both children and adults, the higher the opportunity costs of child rearing are, the higher the value of their health. The rate for population growth decreases and changes from 0.0104 to 0.0037 as a result that b has a stronger effect on the fertility rate than its effect on the mortality rate.

With respect to variations in the parameters that enter the functional form of d, we can argue that changes in the natural mortality rate (L+M) – when the threshold value of L is held constant - from its baseline value of 0.2 to 0.155 and 0.255 yield slight, almost unnoticeable variations in the mortality and the fertility rates. As we might expect, changes in L lead to similar changes in d and n.

The steady-state values of the mortality and fertility rates are quite sensitive to variations in the parameter T, which mainly affect the concavity of the mortality rate function. Changing the parameter T from -0.5 to -1.5 yields a decrease in the mortality rate from 0.0185 to 0.0069 and a fall in the fertility rate from 0.0141 to 0.0238. The greater the absolute value of T the more effective is health expenditure on mortality rate. When T is -1.5, health expenditure is 9.37 and the mortality rate is 0.0069, and when T is -0.5, health expenditure is 28.44 and the mortality rate is 0.0185. For variations in the parameter T, the value of per capita capital remains roughly in the same extent.

Variations in the parameters that affect the utility function - when holding the remainder parameters constant -, which lead to greater per capita health expenditure, also lead to greater per capita capital. From table 1, lower mortality rate and greater per capita capital imply a lower fertility rate. These results support those obtained by Kirk (1996). Parents switch from quantity to quality of children in response to a rise in the rate of human return. Reduced mortality and a healthier population are major contributors to a rise in living standards, which is often regarded as a major factor in fertility decline.

Increasing values of y, f, b, L or T yield increasing values for the steady-state interest rate. In any case, the interest rate does not vary so much when parameters change and the fluctuation ranges from 0.054 to 0.070.

5. Conclusions

In this paper we present a model in which the fertility and the mortality rates are endogenously determined and in which individual choice with respect to health expenditure is introduced. The result reveals a direct relationship between per capita health expenditure and per capita capital. During the transition path both variables evolve in the same direction. If the economy starts from a lower capital per capita point than its steady-state value, per capita health expenditure and capital per capita rise jointly towards their steady-state values, thus the mortality rate declines monotonically until it reaches its stationary value. This movement is consistent with observable evidence of increases in health expenditure and decreases in the mortality rate and in the fertility rate over time.

Per capita health expenditure and per capita income in the steady state are directly related: the greater the health expenditure the greater the income in the steady state. We also observe that a lower mortality rate and a higher per capita capital imply a lower fertility rate. The fertility and mortality rates are correlated in a significant and negative way with the per capita income. As the economy develops, the fertility and the mortality rates fall and are accompanied by an increase in per capita income. These results are in accordance with the assertion that reduced mortality and healthier population are important contributors to higher living standards and increases on productivity, which are often regarded as a major factor in fertility decline.

This paper was received in Feb. and approved in July 2000

The Hamiltonian expression for the general problem is:

The multiplier vector u is the shadow price of capital at any point in time and m is the shadow price of the state variable N. Let P = [N^yc (n - d())^f]^1–q. The conditions for a maximum are:

The transversality conditions are:

Differentiating (2.A) with respect to time, we get:

Substituting u from (2.A) in (5.A), and using this result in (9.A), after simplification and given that 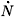/N = n-d() we obtain:

If we consider the logarithmic case, when q = 1, then the above expression may be simplified to:

The transversality condition (7.A) can be expressed using (5.A) as

From (12.A) we derive that the quantity of assets per capita does not grow asymptotically at a rate as high as r–(1+b)n+d(), and that the level of assets does not grow at a rate as high as r–bn.

Substituting u from (2.A) into (3.A), then we obtain that

where . Following the reasoning of Barro and Sala (1995) we arrived at the determination of n. Differentiating (13.A) with respect to time we obtain:

Substituting (13.A) into (6.A), then

which substituted into the latter equation and after simplification, gives:

From (2) we know that 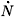/N = n–d(), thus

after some manipulation and taking into account (10.A), we get:

If we consider the logarithmic case, when q = 1, the last equation is simplified, becoming:

The general solution of (15.A), is given by

which is dynamically unstable, because if W(0) departs from its steady-state value -y/r, then W moves over time toward ±¥. Given that q = 1 in (13.A), so that P = 1, we obtain that uN = -e^-rtW. Replacing the solution for W from (16.A) in the transversality condition (8.A), we get:

This equation is verified if and only if W(0) = . Hence, (26) implies that W = . Using the definition of W, we obtain that

Substituting into (4.A) the expressions for u in (2.A) and for m in (13.A), then

which, after simplifying, implies that

where = ke^–xt.

As we have assumed that the derivative of d is a function which is strictly increasing, equation (19.A) shows that there is a one-to-one relationship between and . An increase (decrease) in yields an increase (decrease) in . Taking logarithms in (19.A) and differentiating with respect to time, we obtain

This expression gives us the relationship between the growth rate of capital per capita and the growth rate of health expenditure per capita. Equation (20.A) shows that the growth rate of capital per capita is equal to the magnitude of the elasticity of marginal mortality rate by the growth rate of per capita health expenditure.

Substituting the values for w and r into (11.A) and (3), we obtain a system which can be expressed in terms of variables that are constant in the steady state. Naming = ce^–xt, taking into account that / = /c–x and that = e^–xt –x we obtain system (4), in the logarithmic case.

In order to compute the = 0 locus and the = 0 locus and plot the phase diagram presented in figure 1, we set (5.a) to zero and, solving for , we obtain the = 0 locus

Setting (5.b) to zero and solving for , in order to get the = 0 locus, leads to a quadratic equation in , as follows:

which has two roots:

where

For all the parameters tested in table 1, the larger root turns out to go above the = 0 locus.

• Barro, R. J. & Sala, X. Economic growth New York, McGraw-Hill, 1995.
• Becker, G. S. An economic analysis of fertility. In: Demographic and economic change in developed countries, a conference of universities Princeton, NJ, NBER Committee for Economic Research, Princeton University Press, 1960.
• _______. The demand for children. In: A treatise on the family Cambridge, Harvard University Press, 1991.
• _______ & Barro, R. A reformulation of the economic theory of fertility. Quarterly Journal of Economics, 103:1-25, 1988.
• _______ & Lewis, H. G. On the interaction between the quantity and quality of children. Journal of Political Economy, 81:S279-88, 1973.
• _______; Murphy, K. & Tamura, R. Human capital fertility and economic growth. Journal of Political Economy, 98:S12-37, 1990.
• Caldwell, J. Toward a restatement of demographic transition theory. Population and Development Review, 2:321-66, 1976.
• _______. Theory of fertility decline New York, Academic Press, 1982.
• Cass, D. Optimum growth in an aggregate model of capital accumulation. Review of Economic Studies, 32:233-40, 1965.
• Coale, A. J. Population trends and economic development. In: Menlien, J. (ed.). World population and U.S. policy: the choices ahead New York, Norton, 1986.
• Currais, L. & Rivera, B. Income variation and health expenditure: evidence for OECD countries. Review of Development Economics, 3:258-67, 1999a.
• _______ & _______. Economic growth and health: direct impact or reverse causation. Applied Economic Letters, 6:761-64, 1999b.
• Eckstein, Z. & Wolpin, K. Endogenous fertility and optimal population size. Journal of Public Economics, 27:93-106, 1985.
• Ehrlich, I. Intergenerational trade, longevity and economic growth. Journal of Political Economy, 99:1029-59, 1991.
• _______ & Chuma, H. A model of the demand for longevity and the value of life extension. Journal of Political Economy, 98:761-82, 1990.
• Entwistle, B. & Winegarden, C. R. Fertility and pension programs in LDCs: a model of mutual reinforcement. Economic Development and Cultural Change, 32:331-54, 1984.
• Grossman, M. The demand for health: a theoretical and empirical investigation New York, Columbia University Press, 1972.
• Jablonski, M.; Rosemblum, L. & Kunze, K. Productivity, age, and labor composition changes in the U.S. Monthly Labor Review, 111(9):34-8, 1988.
• Kirk, D. Demographic transition theory. Population Studies, 50:361-87, 1996.
• Koopmans, T. C. On the concept of optimal economic growth. In: The economic approach to development planning Amsterdam, North Holland, 1965.
• Kremer, M. Population growth and technological change: one million B.C. to 1990 1993
• Maddison, A. Monitoring the world economy: 1820-1992. Paris, OCDE, 1995.
• Malthus, T. R. [1798]. An essay on the principle of population London, W. Pickering, 1986.
• Mulligan, C. & Sala, X. Transitional dynamics in two-sector models of endogenous growth. Quarterly Journal of Economics, 434:739-73, 1993.
• Newhouse, J. Medical care expenditure: a cross-national survey. Journal of Human Resources, 12:115-25, 1977.
• Nugent, J. B. The old-age security motive for fertility. Population and Development Review, 11:75-98, 1985.
• Parkin, D.; McGuire, A. & Yule, B. Aggregate health care expenditures and national income. Is health care a luxury good? Journal of Health Economics, 6:109-27, 1987.
• Rostow, W. W. Theorists of economic growth from David Hume to the present New York, Oxford University Press, 1990.
• Schumpeter, J. A. History of economic analysis New York, Oxford University Press, 1954.
• Schultz, T. Changing world prices, women's wages and the fertility transition: Sweden 1860-1910. Journal of Political Economy, 93:1126-54, 1985.
• Smith, A. [1776]. An inquiry into the nature and causes of the wealth of nations New York, Random House, 1937.
• Solow, R. A contribution to the theory of economic growth. Quarterly Journal of Economics, 70:65-94, 1956.
• Willis, R. J. Public and private intergenerational transfers, economic growth and demographic transition. Taipei, Taiwan, Academy Sinica, 1989.
• World Bank. World development reports. New York, Oxford University Press, 1993.

appendix

^*

The author is especially grateful to Jordi Caballe, A. Höfert, Berta Rivera and Manuel Gomez, and participants at the Annual European Economic Association Congress, for discussions and valuable comments. He also thanks support received from La Coruña University, N. 64902-25507.

¹

We do not establish any distinction between child and adult mortality in equation (1). It would be possible to consider nN as the number of new born children, dN as the number of child deaths, and aN as the number of adults deaths, thus

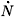= (n-d-a) N. Nevertheless, for simplicity, we focus our analysis on the determination of d, instead of d and a, since this framework does not necessarily imply that individuals that survive birth live forever. The relevant idea is that of infinitely-lived dynasties, rather than infinitely-lived agents.

²

We also developed this model taking into account the existence of both the goods costs of child rearing f and the opportunity cost bk, valued separately. In this case the total cost of child rearing would be defined as: F = f+bk, and f would rise at the rate x per year along with exogenous technological progress, so that f =

e

^xt. Results obtained were quite similar to those presented in this paper, although the equations became more cumbersome. In order to simplify the presentation of the model, we consider only the opportunity costs.

Publication Dates

• Publication in this collection
  31 Aug 2010
• Date of issue
  Dec 2000