ABSTRACT
The one-dimensional skiving stock problem is a combinatorial optimization problem being of high relevance whenever an efficient and sustainable utilization of given resources is intended. In the classical formulation, a given supply of (small) item lengths has to be used to build as many large objects (specified by some target length) as possible. For this 𝒩𝒫-hard (discrete) optimization problem, we investigate the quality of the continuous relaxation by considering the additive integrality gap, i.e., the difference between the optimal values of the integer problem and its LP relaxation. In a first step, we derive an improved upper bound for the gap by focusing on the concept of residual instances. Moreover, we show how further upper bounds can be obtained if all problem-specific input data are considered. Additionally, we constructively prove the integer round-down property for two new classes of instances, and introduce several construction principles to obtain gaps greater than or equal to one.
Keywords:
Cutting and Packing; Skiving Stock Problem; Additive Integrality Gap
1. INTRODUCTION
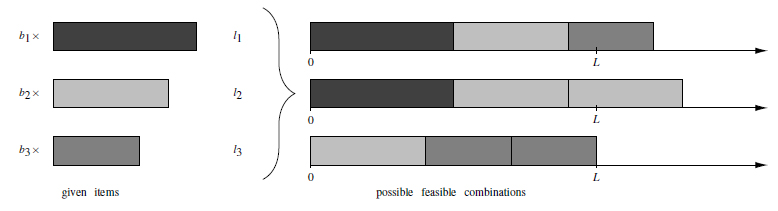
In this paper, we consider an offline version of the one-dimensional skiving stock problem (SSP) 1515. JOHNSON MP, RENNICK C & ZAK EJ. 1997. Skiving addition to the cutting stock problem in the paper industry. SIAM Review, 39(3): 472-483.), (4242. ZAK EJ. 2003. The skiving stock problem as a counterpart of the cutting stock problem. International Transactions in Operational Research , 10: 637-650. which is strongly related to the dual bin packing problem (DBPP) in literature 11. ASSMANN SF, JOHNSON DS, KLEITMAN DJ & LEUNG JYT. 1984. On a dual version of the one-dimensional Bin Packing Problem. Journal of Algorithms, 5: 502-525.), (1717. LABBÉ M, LAPORTE G & MARTELLO S. 1995. An exact algorithm for the dual bin packing problem. Operations Research Letters, 17: 9-18.), (3131. PEETERS M & DEGRAEVE Z. 2006. Branch-and-price algorithms for the dual bin packing and maximum cardinality bin packing problem. European Journal of Operational Research , 170(2): 416-439.. In the classical formulation, different item lengths l i with availabilities are given, the so-called item supply. We aim at maximizing the number of (large) objects with minimum length L that can be constructed by connecting the available items, see Fig. 1. Without loss of generality, all input data are assumed to be positive integers.
According to the typology in 4141. WÄSCHER G, HAUSSNER H & SCHUMANN H. 2007. An improved typology of cutting and packing problems. European Journal of Operational Research , 183: 1109-1130., the two denotations (DBPP and SSP) are separated in the following sense in literature: the term DBPP rather refers to highly heterogeneous input lengths, meaning that the quantities b i are very small (mostly even equal to one) for all , whereas larger values of b i are considered whenever the term SSP is used, in general. This is the same differentiation as in the cutting context, where the bin packing problem and the cutting stock problem are considered.
In general, the skiving stock problem can be considered as a natural counterpart of the extensively studied one-dimensional cutting stock problem (CSP) 88. DELORME M, IORI M & MARTELLO S. 2016. Bin Packing and Cutting Stock Problems: Mathematical Models and Exact Algorithms. European Journal of Operational Research, 255: 1-20.), (1212. GILMORE PC & GOMORY RE. 1961. A Linear programming approach to the cutting-stock problem (Part I). Operations Research, 9: 849-859.), (1616. KANTOROVICH LV. 1960. Mathematical methods of organising and planning production. Management Science, 6: 366-422.), (2727. MARTINOVIC J, SCHEITHAUER G & VALÉRIO DE CARVALHO JM. 2018. A Comparative Study of the Arcflow Model and the One-Cut Model for one-dimensional Cutting Stock Problems. European Journal of Operational Research , 266(2): 458-471.), (3737. SCHEITHAUER G. 2018. Introduction to Cutting and Packing Optimization - Problems, Modeling Approaches, Solution Methods. International Series in Operations Research & Management Science 263, Springer, 1 ed.), (4040. VALÉRIO DE CARVALHO JM. 2002. Lp models for bin packing and cutting stock problems. European Journal of Operations Research , 141(2): 253-273.. Indeed, the latter consists of cutting larger objects into smaller ones, whereas the SSP asks for the reverse direction. Although both problems share a certain common structure (e.g., as regards their input data), they are not dual formulations in the sense of linear optimization. Consequently, the skiving stock problem actually represents an independent problem class within the field of operations research.
First preliminary thoughts on the SSP appeared in the context of paper cutting 1515. JOHNSON MP, RENNICK C & ZAK EJ. 1997. Skiving addition to the cutting stock problem in the paper industry. SIAM Review, 39(3): 472-483.. Some years later, this introductory work led to an ILP formulation (based on the well-known structure of the Gilmore/Gomory model 1212. GILMORE PC & GOMORY RE. 1961. A Linear programming approach to the cutting-stock problem (Part I). Operations Research, 9: 849-859.) for the skiving stock problem containing an infinite number of variables 4242. ZAK EJ. 2003. The skiving stock problem as a counterpart of the cutting stock problem. International Transactions in Operational Research , 10: 637-650.. More sophisticated (pseudo-polynomial) alternative modeling approaches, being able to deal with practically meaningful instance sizes, and detailed computational experiments have recently been presented in 2121. MARTINOVIC J & SCHEITHAUER G. 2016. Integer linear programming models for the skiving stock problem. European Journal of Operational Research , 251(2): 356-368..
Nowadays, the SSP plays an important role whenever an efficient and sustainable use of limited resources is intended. Among others, some main areas of real-world applications are given by: industrial production processes 1515. JOHNSON MP, RENNICK C & ZAK EJ. 1997. Skiving addition to the cutting stock problem in the paper industry. SIAM Review, 39(3): 472-483.), (4242. ZAK EJ. 2003. The skiving stock problem as a counterpart of the cutting stock problem. International Transactions in Operational Research , 10: 637-650., politico-economic problems 11. ASSMANN SF, JOHNSON DS, KLEITMAN DJ & LEUNG JYT. 1984. On a dual version of the one-dimensional Bin Packing Problem. Journal of Algorithms, 5: 502-525.), (1717. LABBÉ M, LAPORTE G & MARTELLO S. 1995. An exact algorithm for the dual bin packing problem. Operations Research Letters, 17: 9-18., or wireless communications 2020. MARTINOVIC J, JORSWIECK E, SCHEITHAUER G & FISCHER A. 2017. Integer Linear Programming Formulations for Cognitive Radio Resource Allocation. IEEE Wireless Communication Letters, 6(4): 494-497.), (3939. TRAGOS EZ, ZEADALLY S, FRAGKIADAKIS AG & SIRIS VA. 2013. Spectrum Assignment in Cognitive Radio Networks: A Comprehensive Survey. IEEE Communications Surveys & Tutorials, 15(3): 1108-1135.. Moreover, the SSP frequently appears side-by-side with the CSP in a holistic cutting-and-skiving scenario within different fields of industry 55. CHEN Y, SONG X, OUELHADJ D & CUI Y. 2019. A heuristic for the skiving and cutting stock problem in paper and plastic film industries. International Transactions in Operational Research, 26(1): 157-179.), (1515. JOHNSON MP, RENNICK C & ZAK EJ. 1997. Skiving addition to the cutting stock problem in the paper industry. SIAM Review, 39(3): 472-483..
2. IMPORTANT DEFINITIONS AND NOTATION
Let with and denote an instance of the skiving stock problem.
Definition 1.Any arrangement of items leading to an object of length not less than L is called (packing) pattern of E.
Obviously, any pattern can be represented by a vector where counts the number of items of type . The set of all patterns is then given by .
Definition 2.A patternis called minimal if there does not exist any patternsuch thatandhold (componentwise). The set of all minimal patterns is denoted by.
Let count how often the minimal pattern of E is used where represents an index set of . Then the standard model of the skiving stock problem 2121. MARTINOVIC J & SCHEITHAUER G. 2016. Integer linear programming models for the skiving stock problem. European Journal of Operational Research , 251(2): 356-368.), (4242. ZAK EJ. 2003. The skiving stock problem as a counterpart of the cutting stock problem. International Transactions in Operational Research , 10: 637-650. can be formulated as
Due to the 𝒩𝒫-hardness of the SSP, a common (approximate) solution approach consists of considering the continuous relaxation
and/or the application of appropriate heuristics. Then, the difference
is called gap (of E), and represents a reasonable measure to evaluate the quality of the LP-based approach.
Remark 1.
-
The gap can also be formulated with respect to other ILP formulations of the skiving stock problem, such as the arcflow model or the one-stick model2121. MARTINOVIC J & SCHEITHAUER G. 2016. Integer linear programming models for the skiving stock problem. European Journal of Operational Research , 251(2): 356-368.. However, due to the equivalence of these three models (and of the corresponding continuous relaxations), see2121. MARTINOVIC J & SCHEITHAUER G. 2016. Integer linear programming models for the skiving stock problem. European Journal of Operational Research , 251(2): 356-368., the gap is the same for them.
-
The optimization problems (1) and (2) can also be formulated on the basis of the complete pattern setor any other pattern setwithwithout changing the respective optimal valuesand . In particular, also the gap does not depend on which pattern set is chosen.
Besides only considering one single instance, frequently the gap of a whole class 𝒯 of instances (e.g. the divisible case, see Def. 4) is of interest, too. In these situations, the gap of 𝒯 shall be understood in the following way:
In particular, 𝒯 may also contain all possible instances.
Similar to the context of one-dimensional cutting, the following definitions (originating from 33. BAUM S & TROTTER LE. 1981. Integer rounding for polymatroid and branching optimization problems. SIAM Journal of Algebraic and Discrete Methods, 2: 416-425.) are of importance:
Definition 3.A set 𝒯 of instances possesses the integer round-down property (IRDP), if holds for all , and it has the modified integer round-down property (MIRDP), ifholds for all. Wheneveris a singleton, we briefly say that E, instead of {E},has the (M)IRDP. An instance E withis called non-IRDP instance.
One of the most important special cases where the MIRDP could successfully be proved is given by the so-called divisible case 2222. MARTINOVIC J & SCHEITHAUER G. 2016. Integer Rounding and Modified Integer Rounding for the Skiving Stock Problem. Discrete Optimization, 21: 118-130..
Definition 4.An instancebelongs to the divisible case (orfor short), ifholds for all.
To exploit these structural properties, in this case an instance can be referred to by its normalized representation with and for .
Remark 2.For any instancethe optimal value of the continuous relaxation is always given by, see2222. MARTINOVIC J & SCHEITHAUER G. 2016. Integer Rounding and Modified Integer Rounding for the Skiving Stock Problem. Discrete Optimization, 21: 118-130.. Hence, only one optimal value remains to be studied for the gap.
Note that the divisible case has also been considered for the cutting stock and the bin packing problem, see 22. BAR-NOY A, LADNER RE & TAMIR T. 2007. Windows Scheduling As a Restricted Version of Bin Packing. ACM Transactions on Algorithms, 3(3): article 28.), (77. COFFMAN JR EG, GAREY MR & JOHNSON DS. 1987. Bin packing with divisible item sizes. Journal of Complexity, 3: 406-428.), (1818. MARCOTTE O. 1983. Topics in combinatorial packing and covering. Technical report, No.568, Cornell University.), (3232. RIETZ J. 2003. Untersuchungen zu MIRUP für Vektorpackprobleme. Ph.D. thesis, Technische Universität Dresden. for some exemplary contributions.
3 MOTIVATION AND CONTRIBUTIONS
Mainly after the publication of the famous book by Nemhauser and Wolsey 2929. NEMHAUSER GL & WOLSEY LA. 1988. Integer and Combinatorial Optimization. Wiley, New York ., a milestone in integer programming (IP), the strength of optimization models has been placed as a central concern in IP modeling and discrete optimization. This idea was new with respect to, for instance, the book by Garfinkel and Nemhauser 1111. GARFINKEL R & NEMHAUSER GL. 1972. Integer Programming. Wiley, New York.. In recent years, research has shown, and it became widely accepted, that
-
the quality of the bound provided by the LP relaxation of the IP model is a crucial factor in the size of the search trees in branch-and-bound, and
-
in general, strong models have a better behavior when the size of the instances grows. More precisely, if two models have a similar behavior (in terms of computational time) for a given size of instances, one can anticipate that the stronger model will perform better than the weaker model for larger instances.
Consequently, judging solution strategies for 𝒩𝒫-hard problems by the empirical method (i.e., by computational experiments covering a significant set of instances, including those that represent the limits of what can be solved in a reasonable amount of time) is important, but providing theoretical justifications that the considered formulations are strong is (in many cases) a guarantee that, as instances grow, the computational times do not rise so sharply as they would with weaker ones.
Remark 3. Some of the previous claims are implicitly based on the assumption that the efforts to generate and solve the considered relaxations do not differ significantly from one another. More generally, from a computational point of view, it is also very important to find a reasonable balance between the quality of the bound obtained by a given relaxation and the time required to solve this relaxation (at each node of the search tree). For instance, this trade-off can be observed when dealing with the well-known asymmetric traveling salesman problem, where those MILP models providing the best (lower) bounds 13 13. GODINHO MT, GOUVEIA L & PESNEAU P. 2011. On a Time-Dependent Formulation and an Updated Classification of ATSP Formulations. In: MAHJOUB R (Ed.), Progress in Combinatorial Optimization, Wiley. ), ( 38 38. SHERALI HD, SARIN SC & TSAI PF. 2006. A class of lifted path and flow-based formulations for the asymmetric traveling salesman problem with and without precedence constraints. Discrete Optimization , 3(1): 20-32. require high solution times even for small instances (with less than 40 nodes), so that they are outperformed by much weaker approaches (with respect to the bound) 28 28. MILLER CE, TUCKER AW & ZEMLIN RA. 1960. Integer Programming Formulation of Traveling Salesman Problems. Journal of the ACM, 7(4): 326-329. ), ( 36 36. ROBERTI R & TOTH P. 2012. Models and algorithms for the Asymmetric Traveling Salesman Problem: an experimental comparison. EURO Journal on Transportation and Logistics, 1(1-2): 113-133. .
As regards, for instance, the well-known cutting stock problem (and the related bin packing problem) a significant body of work on the additive integrality gap has been established in recent decades. For a period of more than 20 years, it was conjectured that the gap of the CSP can be bounded above by the constant 1. The first counterexample to this claim (a so-called non-IRUP instance) was found by Marcotte 1818. MARCOTTE O. 1983. Topics in combinatorial packing and covering. Technical report, No.568, Cornell University., but it required input data in the range of 106. Hence, research on the gap of the CSP was still considered to be rather unimportant, particularly due to the non-appearance of such data in practical cases, and (as discussed above) due to the fact that the scientific attention was not yet sufficiently focussed on the performance of relaxations. Some years later, also under the influence of the agenda presented by 2929. NEMHAUSER GL & WOLSEY LA. 1988. Integer and Combinatorial Optimization. Wiley, New York ., Fieldhouse 1010. FIELDHOUSE M. 1990. The duality gap in trim problems. SICUP-Bulletin, 5: 4-5. and Nica 3030. NICA V. 1994. A General counterxample to the Integer Round-Up property, working paper, Department of Economic Cybernetics, Academy of Economic Studies, Bucharest. constructed the first counterexamples of moderately sized input data. Afterwards, research on the gap of the CSP was further intensified such that more and more articles dealt with the construction of large gaps 44. CAPRARA A, DELL’AMICO M, DIAZ-DIAZ JC, IORI M & RIZZI R. 2015. Friendly bin packing instances without Integer Round-up Property. Mathematical Programming, 150: 5-17.), (3333. RIETZ J & DEMPE S. 2008. Large gaps in one-dimensional cutting stock problems. Discrete Applied Mathematics , 156(10): 1929-1935.), (3434. RIETZ J, SCHEITHAUER G & TERNO J. 2002. Families of non-IRUP instances of the one-dimensional cutting stock problem. Discrete Applied Mathematics , 121: 229-245. or upper bounds for the maximal gap 3232. RIETZ J. 2003. Untersuchungen zu MIRUP für Vektorpackprobleme. Ph.D. thesis, Technische Universität Dresden.), (3535. RIETZ J, SCHEITHAUER G & TERNO J. 2002. Tighter Bounds for the Gap and Non-IRUP Constructions in the One-dimensional Cutting Stock Problem. Optimization, 51(6): 927-963..
Since, contrary to that, the skiving stock problem represents a relatively young field of research, not having attracted a comparable scientific interest so far, there is no specific preliminary work on its gap in the related literature (apart from own articles). However, in a very recent publication 99. EISENBRAND F & WEISMANTEL R. 2017, Proximity results and faster algorithms for Integer Programming using the Steinitz Lemma. Available online: https://arxiv.org/abs/1707.00481.
https://arxiv.org/abs/1707.00481...
, maximization problems of type
with arbitrary , and upper bounds , are investigated with special emphasis on their additive integrality gap . As a consequence of [99. EISENBRAND F & WEISMANTEL R. 2017, Proximity results and faster algorithms for Integer Programming using the Steinitz Lemma. Available online: https://arxiv.org/abs/1707.00481.
https://arxiv.org/abs/1707.00481...
, Theorem 6 and Subsect. 3.1], the currently best known upper bound results to
with
For the SSP, where A denotes the pattern matrix, this observation together with the problem-specific data and (and, for instance, ) lead to
for any instance E, i.e., to an upper bound of nonpolynomial order. However, the largest known gap is currently given by , see 2323. MARTINOVIC J & SCHEITHAUER G. 2016. The Proper Relaxation and the Proper Gap of the Skiving Stock Problem. Mathematical Methods of Operations Research , 84(3): 527-548., and hence the SSP is conjectured to possess the MIRDP. Consequently, the facts provided by this quite general approach 99. EISENBRAND F & WEISMANTEL R. 2017, Proximity results and faster algorithms for Integer Programming using the Steinitz Lemma. Available online: https://arxiv.org/abs/1707.00481.
https://arxiv.org/abs/1707.00481...
are far away from being of sufficient quality to obtain reasonable theoretical results for the gap of the SSP.
Similar to the CSP, a verification of for arbitrary instances (or the presentation of a counterexample) of the SSP is actually very difficult. More precisely, the inequality (see 2424. MARTINOVIC J & SCHEITHAUER G. 2017. LP-based Relaxations of the Skiving Stock Problem - Improved Upper Bounds for the Gap. Operations Research Proceedings 2015, pp. 49-54.) currently represents the best upper bound being available for the case of general instances. Due to this hardness, two main directions of research have been established in literature:
-
proving the IRDP or the MIRDP for special classes of instances, see 2222. MARTINOVIC J & SCHEITHAUER G. 2016. Integer Rounding and Modified Integer Rounding for the Skiving Stock Problem. Discrete Optimization, 21: 118-130. or 4242. ZAK EJ. 2003. The skiving stock problem as a counterpart of the cutting stock problem. International Transactions in Operational Research , 10: 637-650., and
-
investigating construction principles for instances with gaps larger than or equal to one, see 2323. MARTINOVIC J & SCHEITHAUER G. 2016. The Proper Relaxation and the Proper Gap of the Skiving Stock Problem. Mathematical Methods of Operations Research , 84(3): 527-548.), (2222. MARTINOVIC J & SCHEITHAUER G. 2016. Integer Rounding and Modified Integer Rounding for the Skiving Stock Problem. Discrete Optimization, 21: 118-130..
One of the most important special cases where the MIRDP could successfully be proved is given by the divisible case 2222. MARTINOVIC J & SCHEITHAUER G. 2016. Integer Rounding and Modified Integer Rounding for the Skiving Stock Problem. Discrete Optimization, 21: 118-130.), (2525. MARTINOVIC J & SCHEITHAUER G. 2017. An Upper Bound of ∆(E) < 3/2 for Skiving Stock Instances of the Divisible Case. Discrete Applied Mathematics, 229: 161-167..
Within this paper, we address and present several new results related to the gap of the skiving stock problem, especially with respect to the IRDP and the MIRDP. Besides possessing theoretical importance these results are of practical interest as well. For example, if the IRDP of an instance E is known, then the optimal value of the (hard) integer problem (1) can easily be otained by solving the linear program (2) and applying . Similarly, the MIRDP of an instance E only allows the two possibilities for the optimal value of the integer problem. However, the computation of a corresponding feasible integer solution may still be difficult in some cases. Most notably, the following main achievements will be presented:
-
Compared to the inequality from 2424. MARTINOVIC J & SCHEITHAUER G. 2017. LP-based Relaxations of the Skiving Stock Problem - Improved Upper Bounds for the Gap. Operations Research Proceedings 2015, pp. 49-54., the improved upper bound (with an instance-specific parameter ) for arbitrary instances E is derived in Subsection 4.2.
-
Subsection 4.3 introduces new upper bounds for the gap of general instances that make use of all problem-specific input data of a given instance E (i.e., not only the quantity m is used as it is the case in all currently available bounds from literature 2424. MARTINOVIC J & SCHEITHAUER G. 2017. LP-based Relaxations of the Skiving Stock Problem - Improved Upper Bounds for the Gap. Operations Research Proceedings 2015, pp. 49-54.), (2222. MARTINOVIC J & SCHEITHAUER G. 2016. Integer Rounding and Modified Integer Rounding for the Skiving Stock Problem. Discrete Optimization, 21: 118-130.), (4242. ZAK EJ. 2003. The skiving stock problem as a counterpart of the cutting stock problem. International Transactions in Operational Research , 10: 637-650.). Remarkably, this new approach (for arbitrary instances) is based on the well-studied divisible case.
-
In Section 5, two new classes of instances (the so-called strongly divisible and semi-divisible instances) are constructively shown to possess the IRDP.
-
Section 6 presents various new construction principles for gaps larger than or equal to one. Interestingly, this also includes the first published classes of non-IRDP instances not belonging to the divisible case.
In a final step, we summarize the most important contributions, give some conclusions and provide an outlook on future research.
4 UPPER BOUNDS FOR THE GAP OF THE SKIVING STOCK PROBLEM
4.1 Residual Instances and a Short Overview on Existing Upper Bounds
In this subsection, we reformulate the (approximate) calculation of the gap of an instance by replacing this instance E with an instance having principally the same input data, but a (appropriately) reduced vector of availabilities. Hence, due to the smaller total number of objects, the optimization problem becomes more manageable in a certain extent. On the other hand, the new gap only provides an upper bound for , in general. As an initial point, we describe the construction of more precisely.
Definition 5. Let be an instance of the skiving stock problem, and let x c denote a solution of the corresponding continuous relaxation (2). If x c is an extreme point of the feasible region of problem (2), then the instance
withis called residual instance of E. The set of all residual instances of a given instance E is denoted by ℛ(E).
Remark 4.Whenever xcis a solution but not an extreme point of the feasible region of (2), the definition of a residual instance would still make sense. The crucial property that will be required in some of the results presented below is that xc(as an extreme point) possesses at most m positive components which will, in particular, lead to the inequality. In order to see that the latter does not have to hold for arbitrary solutions xc, consider the instance. Here, we havewhich is, for instance, provided by the following solution
In this case, xcis not an extreme point and we have. Hence, the vector of the residual instance is given by. For this specific residual instance, we now obtainwhich is for instance provided by the decomposition
Hence, an extreme point xchas to be chosen to obtainfor. To provide an example, we could take
leading toand the optimal value.
However, assuming an extreme point does not represent an actual restriction. On the one hand, any solvable problem of type (2) always possesses an extreme point within the set of its solutions. On the other hand, from a practical point of view, solutions of (2) are usually found by the simplex method and column generation, so that at most m positive components will be obtained anyway.
In addition to the previous remark, the following points shall be emphasized:
-
From a theoretical point of view, we formally allow (for some ) for residual instances in order to maintain a constant number m of item types.
-
The term denotes the matrix whose columns are equal to the elements of P*(E), i.e., to the minimal patterns of the given instance E. Observe that, for the sake of simplicity, we will not make any distinction between the system matrix A of the original instance E and that of the considered residual instance . Even if is non-empty (which occurs if and only if holds for some ), the patterns from can theoretically be added to the system matrix of without changing the optimal value of the LP or the ILP. This holds since their related counting variables x j will satisfy in any (integer or continuous) feasible solution of .
-
It is straightforward to show that the continuous relaxation of is solved by .
As presented in 2424. MARTINOVIC J & SCHEITHAUER G. 2017. LP-based Relaxations of the Skiving Stock Problem - Improved Upper Bounds for the Gap. Operations Research Proceedings 2015, pp. 49-54. we obtain the following relationship between the gaps of an instance and one of its residual instances.
Lemma 1.Let, thenholds. In particular, the following implications are true:
-
If has the IRDP, then E has the IRDP.
-
If has the MIRDP, then E has the MIRDP.
Proof. Let be a solution of . Then, with is feasible for E due to and . Furthermore, we have
With this inequality and the fact that holds for the optimal values of the continuous relaxations (as indicated in the third point of the above list), we obtain
and the proof is complete. □
Hence, the gap of an instance E can be bounded above by the gap of any corresponding residual instance . Thus, the consideration of residual instances is sufficient for our purposes.
To our best knowledge, the first general upper bound for the gap of an arbitrary instance was given in [2222. MARTINOVIC J & SCHEITHAUER G. 2016. Integer Rounding and Modified Integer Rounding for the Skiving Stock Problem. Discrete Optimization, 21: 118-130., Theorem 1]. Therein, an idea of [4242. ZAK EJ. 2003. The skiving stock problem as a counterpart of the cutting stock problem. International Transactions in Operational Research , 10: 637-650., Theorem 4] could successfully be generalized to .
Theorem 1.Letwithbe given and letbe an arbitrary instance with m types of item lengths. Thenholds.
On the basis of residual instances, this result could be improved in [2424. MARTINOVIC J & SCHEITHAUER G. 2017. LP-based Relaxations of the Skiving Stock Problem - Improved Upper Bounds for the Gap. Operations Research Proceedings 2015, pp. 49-54., Theorem 3].
Theorem 2.Letbe an instance of the skiving stock problem, then.
If the item lengths are known to be sufficiently small, we can state the following special case of the previous result [2424. MARTINOVIC J & SCHEITHAUER G. 2017. LP-based Relaxations of the Skiving Stock Problem - Improved Upper Bounds for the Gap. Operations Research Proceedings 2015, pp. 49-54., Corollary 3].
Corollary 1.Letwithbe given. Ifholds for all, then the gap satisfies the inequality
4.2 An Improved Upper Bound
An obvious possibility to obtain a feasible integer solution on the basis of a given solution x c of the continuous relaxation consists of rounding down each variable to the nearest integer. This method was also applied in the proof of Theorem 1, see 2222. MARTINOVIC J & SCHEITHAUER G. 2016. Integer Rounding and Modified Integer Rounding for the Skiving Stock Problem. Discrete Optimization, 21: 118-130. for more details. In what follows, we aim at evaluating the quality of this approach in terms of the resulting gap. As a starting point, we need the following lemma.
Lemma 2.Letbe an instance of the skiving stock problem withfor some. Then we have.
Proof. We consider two cases:
Case 1: ρ is even
In this case, we have for some . Since any minimal pattern satisfies we certainly can build τ patterns out of the given items. But, after this, there will still remain items of total length greater than , i.e., at least one additional pattern can be obtained. Hence, we have
due to and the assumption of this case.
Case 2: ρ is odd
In this case, we have for some . Since any minimal pattern satisfies we certainly can build τ patterns out of the given items. Hence, we have
-
due to and the assumption of this case. □
This lemma can be used to prove the following theorem.
Theorem 3.Letbe an instance of the skiving stock problem with, and let xcdenote a solution of the continuous relaxation (2). If
holds for some, thenis satisfied.
Proof. We have for some implying that has to hold (due to Lemma 2). But this immediately leads to
Obviously, Theorem 3 holds for all instances of the skiving stock problem, particularly for residual ones. This (trivial) observation has an important implication which improves the upper bound of Theorem 2.
Corollary 2. Let denote an instance of the skiving stock problem. Then
holds, where denotes the minimal number of (remaining) different item types in a residual instance of E.
Proof. Let represent a residual instance of E that possesses exactly β different remaining item types. According to a previous observation, we know that is a solution of the continuous relaxation of with (in a componentwise sense). In a first step, we show that has at most β nonzero components. To this end, consider an arbitrary but fixed index with (i.e., the items of type i do actually not appear anymore in the residual instance), and note that the solution x c has to satisfy . Based on the definition of the vector , see Def. 5, we have which implies that has to hold for any pattern with . But now, at least one non-zero component of x c has to belong to a pattern j * with in order to ensure for the value given by the instance E. Consequently, we obtain that and have to hold, so that has at most m − 1 positive components. By an iterative continuation of this procedure we finally obtain that has at most β non-zero components.
According to this observation (and ), we have . Hence, there exists with
implying
due to Theorem 3. □
This approach leads to an improvement of the previous upper bound (see 2424. MARTINOVIC J & SCHEITHAUER G. 2017. LP-based Relaxations of the Skiving Stock Problem - Improved Upper Bounds for the Gap. Operations Research Proceedings 2015, pp. 49-54.) , at least for all instances where m is even. Note that, due to , the situation appears if and only if
holds for some . The latter is likely to be satisfiable especially for highly heterogeneous instances, i.e., where the values b i are close to (or equal to) 1. However, even though in some cases there are easily computable residual instances possessing strictly less item types than the original instance E, the exact value β will be hard to find, in general.
Remark 5.Even after several decades of extensive research, the best known upper bound for the gap of the related cutting stock problem is also given by 𝒪(m) (but with a constant of 1/4), see3535. RIETZ J, SCHEITHAUER G & TERNO J. 2002. Tighter Bounds for the Gap and Non-IRUP Constructions in the One-dimensional Cutting Stock Problem. Optimization, 51(6): 927-963..
Note that whenever holds for some , we cannot obtain a better result than in the worst case. Hence, further improvements of the presented upper bound require different approaches. One of them will be introduced in the next subsection.
4.3 An Approach based on the Divisible Case
Besides the issue discussed in the previous subsection, one of the main drawbacks of all the existing upper bounds from literature is the fact that they do not use any information about the other given input data, such as the vectors l and b. This means that, for constant m, the upper bound is always the same regardless of how the further parameters look like. In this subsection we aim at constructing an upper bound that uses as many of the given information as possible. To this end, let be an instance of the skiving stock problem. Then we consider the instance where is given by . Due to this construction, it is possible that different item lengths lead to the same modified length . In order to maintain a constant number m of items, these objects shall formally be treated as different, in general. Note that E 𝒟𝒞 can also be interpreted as an instance, even if we have , in general.
Lemma 3.The inequalityholds for all.
Proof. Let be arbitrarily chosen but fixed. Then we have the equivalence
and the latter is true due to
Corollary 3.The inequalitiesandhold.
Proof. Due to , we have for the pattern sets of both instances. Hence, any feasible (integer) solution of E 𝒟𝒞 is also a feasible (integer) solution of E which proves the assertion. □
Remark 6.In the previous proof we applied that the optimal objective values of (1) and (2) are independent of the fact, whether P(E) or P* (E) is used (see also Remark 1) as the pattern set. This is important since the inclusiondoes not necessarily have to hold for any instance E. By way of example, consider the instancewith. Here we have, but notsince the item of lengthcan be removed.
Note that E 𝒟𝒞 is an instance of the well-studied divisible case since
holds for all . Thus, we can state
due to the properties of the divisible case. More precisely, we use that any instance satisfies , see Remark 2, and , see [26, Theorem 3]. These preliminaries lead to the following result.
Theorem 4. Let be an instance of the skiving stock problem, denote one of its residual instances, and let be constructed as above. Then
holds. In the second case, we particularly have
Proof. Let us consider the case at first. Then we have
which proves the inequality. On the other hand, observe that holds by construction for any , so that we directly obtain the second upper bound.
Whenever holds, the previous approach would lead to a division by zero (in the second summand) and cannot be applied. However, note that in this case, we have so that the difference is equal to as a consequence of the divisible case. □
There are still at least two main possibilities to further improve the upper bounds presented by (7):
-
The first two terms of (7) can be decreased if it is possible to find a better upper bound for the gap of the divisible case. For instance, in the related context of one-dimensional cutting, has been proved for the whole divisible case, but it has only been published in German language as a contribution of the PhD thesis 3232. RIETZ J. 2003. Untersuchungen zu MIRUP für Vektorpackprobleme. Ph.D. thesis, Technische Universität Dresden. (However, at least a short hint on the existence of this upper bound can be found at the end of the introductory section in 3333. RIETZ J & DEMPE S. 2008. Large gaps in one-dimensional cutting stock problems. Discrete Applied Mathematics , 156(10): 1929-1935..). So far, it is not known whether a similar result can be shown for the skiving stock problem, too. On the other hand, the currently largest known gap for the divisible case of the skiving stock problem is given by > (for arbitrarily small values of ), see 2222. MARTINOVIC J & SCHEITHAUER G. 2016. Integer Rounding and Modified Integer Rounding for the Skiving Stock Problem. Discrete Optimization, 21: 118-130.. Both aspects give hope that further improvements are possible. Note that in the special case where consists of only two item types, i.e., , the first two summands of (7) can be replaced by 1 due to Theorem 1.
-
A very weak inequality, used in the previous estimate, is
-
since the absolute difference of both terms may be large. Thus, the upper bound (7) can be improved significantly if, for instance, a constant could be found.
Nevertheless, Theorem 4 provides an upper bound that uses all of the input data and improves the bound given by Theorem 3 in some cases. As a conclusion of this section, the latter shall be investigated in more detail.
Remark 7.First of all note that there are numbersso that holds for any . For example, we can always choosewhere, but depending on the particular residual instancebetter choices of α i can be possible. Then, the ideas of the previous proof lead to
wherewas used in the last line. Now, it can be seen that this bound is better than, if for instance
-
the availabilitiesare small:More precisely, by assuming thatholds for someand all , we obtain
-
because of . By choosing , we obviously obtain a better upper bound.
-
the instance is close to the divisible case: So far, we only dealt with the worst-case , but in many scenarios the values α i are (much) smaller. In other words, this would mean that the differencesare rather close to zero, so thatis close to the divisible case. If, for instanceholds for someand all , then we obtain
-
which is better thanif and only if .
Furthermore, observe that also small values of β directly decrease the upper bounds presented in (7) since the summations contain a fewer number of non-zero terms.
5 NEW CLASSES OF INSTANCES POSSESSING THE IRDP
As mentioned in the introductory sections, the skiving stock problem is conjectured to satisfy for all instances E. Computational simulations 2121. MARTINOVIC J & SCHEITHAUER G. 2016. Integer linear programming models for the skiving stock problem. European Journal of Operational Research , 251(2): 356-368.), (4242. ZAK EJ. 2003. The skiving stock problem as a counterpart of the cutting stock problem. International Transactions in Operational Research , 10: 637-650. have shown that many instances even possess a gap less than one (i.e., they have the IRDP); whereas instances with gaps (significantly) larger than one are hard to find, in general. Note that the optimal objective value of (1) can easily be calculated by for IRDP instances; and hence a deeper insight on those instances is desirable. Observe that there is only a single result known in literature [4242. ZAK EJ. 2003. The skiving stock problem as a counterpart of the cutting stock problem. International Transactions in Operational Research , 10: 637-650., Theorem 4] concerning the IRDP of a very simple class of instances which now is, in fact, a direct consequence of Corollary 2.
Lemma 4.Any instancepossesses the IRDP.
Admittedly, instances consisting of only two different item types are very rare, and may (if at all) only appear as residual instances for practically meaningful scenarios. To cope with larger values of m, the following two results provide some obvious (but new) observations:
Lemma 5.Letbe an instance with. Then E has the IRDP.
Proof. If holds, we have . In the other case where holds, we also have implying that the given item supply is sufficiently large to build one pattern. Hence, we obtain . □
Note that, besides allowing arbitrary values of m, the condition of Lemma 5 is also less restrictive than that of Lemma 4. In fact, any residual instance satisfies the inequality of Lemma 5.
Lemma 6.Letbe an instance withfor alland some, then E has the IRDP.
Proof. Observe that we need exactly k items to build a minimal pattern of E, and hence we obtain . Now let us assume that holds for a solution x* of the continuous relaxation (2). Then we have
which gives the contradiction. Altogether, we obtain
i.e., E has the IRDP. □
In the remainder of this section we want to prove the IRDP for two new classes of instances which can be seen as special representatives of the divisible case.
Definition 6. An instance of the skiving stock problem is called
-
weakly divisible, ifholds for all .
-
strongly divisible, if it is weakly divisible and ifis satisfied.
-
semi-divisible, ifholds for all , and if there exists a partitionwithandsuch that
are satisfied.
Remark 8. Observe the following relationships:
-
Each strongly divisible instance is also weakly divisible and semi-divisible. The reversions are not true in general.
-
Each semi-divisible instance E can be decomposed into two strongly divisible instances E 1 and E 2 , where
Note that, although appearing rather restrictive, the instance types appearing in Definition 6 may (in part) be relevant for practical tasks as well. For instance, in terms of assigning secondary users to vacant frequency intervals 2020. MARTINOVIC J, JORSWIECK E, SCHEITHAUER G & FISCHER A. 2017. Integer Linear Programming Formulations for Cognitive Radio Resource Allocation. IEEE Wireless Communication Letters, 6(4): 494-497.), (3939. TRAGOS EZ, ZEADALLY S, FRAGKIADAKIS AG & SIRIS VA. 2013. Spectrum Assignment in Cognitive Radio Networks: A Comprehensive Survey. IEEE Communications Surveys & Tutorials, 15(3): 1108-1135., the resulting instances can sometimes belong to those classes due to a high degree of standardization in wireless communications. Moreover, such instances have also attracted scientific interest with respect to the related one-dimensional cutting stock problem 1818. MARCOTTE O. 1983. Topics in combinatorial packing and covering. Technical report, No.568, Cornell University.), (1919. MARCOTTE O. 1985. The cutting stock problem and integer rounding. Mathematical Programming , 33(1): 82-92..
At first we want to prove the IRDP for strongly divisible instances (with the representation , i.e., with . Therefore, the first fit decreasing (FFD) algorithm, proposed in 11. ASSMANN SF, JOHNSON DS, KLEITMAN DJ & LEUNG JYT. 1984. On a dual version of the one-dimensional Bin Packing Problem. Journal of Algorithms, 5: 502-525. for the dual bin packing problem, represents an initial point of our further investigations. Note that this heuristic was also successfully applied to prove the modified integer round-down property (MIRDP) for the divisible case 2222. MARTINOVIC J & SCHEITHAUER G. 2016. Integer Rounding and Modified Integer Rounding for the Skiving Stock Problem. Discrete Optimization, 21: 118-130.. In this algorithm, given an instance normalized to with , bins of capacity are filled successively.
Definition 7. A bin B is called filled if the objects allocated to it possess a total length of at least l B . If this total length equals l B , the bin B is said to be filled exactly. Furthermore, we say that a bin B can accept an object if, after adding this item, the total length of all objects in B does not exceed l B .
Note that after Phase II each non-empty bin contains objects of total length not less than . Hence, each bin can be interpreted as a uniquely determined packing pattern of E. Actually, observe that all bins but possibly the very last one correspond to a minimal pattern. However, by successively removing appropriate items, also the last non-empty bin can easily be reduced to a minimal pattern.
Remark 9.Note that there are further good heuristics especially for the divisible case, e.g., a best-fit decreasing algorithm introduced in2525. MARTINOVIC J & SCHEITHAUER G. 2017. An Upper Bound of ∆(E) < 3/2 for Skiving Stock Instances of the Divisible Case. Discrete Applied Mathematics, 229: 161-167.. However, for our theoretical purposes the properties provided by Algorithm 1 are sufficient.
Lemma 7.Let E be strongly divisible. After the completion of Phase I of Algorithm 1 the following statement holds: The remaining capacity of any bin is given by a nonnegative multiple of the smallest item length that is contained in the considered bin.
Proof. Let q denote the number of bins after Phase I, and let be fixed. Let l(j) denote the smallest item length allocated to bin B j . Then there is with . Since E is strongly divisible, there are natural numbers with and for all . Let denote the number of objects of length li in Bj, then the remaining capacity R(j) of B j satisfies
This implies and we are done. □
Observe that, actually, even a stronger version of the statement can be proved by the same arguments. More precisely, it also holds that any possible partial filling of a bin possesses the property mentioned in the previous lemma.
By means of Algorithm 1 (not necessarily with ) and the Lemma 7, the IRDP of strongly divisible instances can be shown.
Theorem 5.Let E be strongly divisible, then E possesses the IRDP.
Proof. Let denote the number of bins after Phase I, and let
For all bins are filled exactly which means . Consequently, we obtain
i.e., E has the IRDP.
Now consider the case . At first we prove that has to hold in this case: For the sake of contradiction let us assume . Then we consider the bin B j and define
where ñ and are defined as in Phase I of Algorithm 1. Due to we have . According to Lemma 7, the remaining capacity R(j) has to be a nonnegative multiple of , i.e., there exists ( is not possible since B j is not filled exactly) with . But now the object must have also been allocated to B j in Phase I since all previous bins are filled exactly and This means that k was not maximal which gives the contradiction.
Consequently, only the very last bin is not filled exactly which ensures . On the other hand this observation shows leading to
and we are done. □
Based on this result we can now cope with semi-divisible instances .
Theorem 6.Let E be a semi-divisible instance, then E possesses the IRDP.
Proof. The main idea of the proof is to apply Algorithm 1 to the two strongly divisible subinstances of E separately, and then to possibly add a single post-processing step. The full details and the resulting case study can be found in the appendix APPENDIX: PROOF OF THEOREM 6 We consider the decomposition of point (ii) in Remark 8 and apply Phase I of Algorithm 1 on E 1 and E 2 separately. Let qi(i∈{1,2}) denote the number of bins of subinstance E i , then we either have Ri(qi)=0 or 0<Ri(qi)<L, where R i (q i ) denotes the remaining capacity of the last bin Bqi of instance E i . Case 1: The equality R1(q1)=R2(q2)=0 holds. In this case, both instances possess only bins that are filled exactly, i.e., we have (li)⊤bi=qi·L for i∈{1,2} . Hence we obtain z*(E)≥q1+q2 leading to Δ ( E ) = z c * ( E ) − z * ( E ) ≤ l ⊤ b L − ( q 1 + q 2 ) = ∑ i = 1 2 ( ( l i ) ⊤ b i L − q i ) = 0, i.e., the IRDP of E. Case 2: There is exactly one index i∈{1,2} with Ri(qi)=0 . Without loss of generality we assume R1(q1)=0 . Then we have (l1)⊤b1=q1·L , and due to the observations in the proof of Theorem 5 we further obtain 0 < ( l 2 ) ⊤ b 2 L − ( q 2 − 1 ) < 1. Combining these feasible solutions of the subinstances results to z*(E)≥q1+q2−1 implying that Δ ( E ) = z c * ( E ) − z * ( E ) ≤ l ⊤ b L − ( q 1 + q 2 − 1 ) = ( l 2 ) ⊤ b 2 L − ( q 2 − 1 ) < 1 has to hold, i.e., E has the IRDP. Case 3: The inequalities R1(q1)>0 and R2(q2)>0 hold. As in the previous case, the proof of Theorem 5 leads to 0 < ( l i ) ⊤ b i L − ( q i − 1 ) < 1. for i∈{1,2} . Now there are again two cases Subcase 3.1: Let ∑ i = 1 2 ( ( l i ) ⊤ b i L − ( q i − 1 ) ) < 1 be satisfied. Then a combination of the feasible solutions of the two subinstances leads to z*(E)≥(q1−1)+(q2−1) . Thus we obtain Δ ( E ) = z c * ( E ) − z * ( E ) ≤ l ⊤ b L − ( q 1 − 1 + q 2 − 1 ) = ∑ i = 1 2 ( ( l i ) ⊤ b i L − ( q i − 1 ) ) < 1, i.e. the IRDP of E. Subcase 3.2: 2 > ∑ i = 1 2 ( ( l i ) ⊤ b i L − ( q i − 1 ) ) ≥ 1 be satisfied. By joining the items of the bins q 1 from E 1 and q 2 from E 2 we obtain an additional filled bin. A combination of all bins leads to z*(E)≥(q1−1)+(q2−1)+1=q1+q2−1 , implying that Δ ( E ) = z c * ( E ) − z * ( E ) ≤ l ⊤ b L − ( q 1 + q 2 − 1 ) = ∑ i = 1 2 ( ( l i ) ⊤ b i L − ( q i − 1 ) ) − 1 < 2 − 1 = 1, i.e., E has the IRDP. □ . □
Note that the previous proofs do not only state the IRDP of the considered instances, but they also provide a direct method to construct the corresponding integer solution (based on the FFD heuristic) in the various cases.
Remark 10.Observe that this method cannot be generalized to instances E consisting ofstrongly divisible subinstances. Indeed, if we considerand the instance, then it is not possible to build two feasible patterns out of the given items, see [2222. MARTINOVIC J & SCHEITHAUER G. 2016. Integer Rounding and Modified Integer Rounding for the Skiving Stock Problem. Discrete Optimization, 21: 118-130., Remark 3].
For the one-dimensional cutting stock problem, also weakly divisible instances are known to possess the IRUP (integer round-up property), see 1818. MARCOTTE O. 1983. Topics in combinatorial packing and covering. Technical report, No.568, Cornell University. for a proof based on polyhedral theory. Whether an analogue statement holds in the context of one-dimensional skiving has to remain open at this point. Perhaps such a result can be proved by induction over L, since the induction basis belongs to the family of strongly divisible instances.
6 NEW CONSTRUCTION PRINCIPLES FOR FAMILIES OF NON-IRDP INSTANCES
In consideration of the upper bound developed in Section 4, a direct verification of the property for general instances seems to be very hard. Instead, another approach to tackle the MIRDP conjecture is given by the investigation of conditions ensuring that a given instance does not possess the IRDP. Perhaps, such construction principles may (in future) be valuable when striving to find instances with gaps close to (or larger than) 2.
6.1 Construction Principles based on the Cutting Stock Problem
So far, only construction methods for non-IRDP instances of the divisible case are known in literature, see 2222. MARTINOVIC J & SCHEITHAUER G. 2016. Integer Rounding and Modified Integer Rounding for the Skiving Stock Problem. Discrete Optimization, 21: 118-130.. In this subsection, we aim at presenting families of parametrized instances not belonging to the divisible case, but possessing a gap , which actually represents the first systematic approach to obtain more general non-IRDP instances. These instances have also been studied in the context of one-dimensional cutting by J. Rietz and co-authors, see 3333. RIETZ J & DEMPE S. 2008. Large gaps in one-dimensional cutting stock problems. Discrete Applied Mathematics , 156(10): 1929-1935. and 3434. RIETZ J, SCHEITHAUER G & TERNO J. 2002. Families of non-IRUP instances of the one-dimensional cutting stock problem. Discrete Applied Mathematics , 121: 229-245. for some of the results, so that the corresponding proofs would only require minor changes in almost all cases. However, we also emphasize that some other constructions to be introduced here are only contained in the German-language PhD thesis 3232. RIETZ J. 2003. Untersuchungen zu MIRUP für Vektorpackprobleme. Ph.D. thesis, Technische Universität Dresden., and hence they have never been made available (not even for the CSP case) to a broad scientific community.
In order to see how all the sets of instances can be used in the skiving framework, we need the following two results.
Lemma 8. The following assertions hold:
-
Letbe an instance of the one-dimensional cutting stock problem with . Then alsoholds if E is interpreted as an instance of the one-dimensional skiving stock problem.
-
Letbe an instance of the one-dimensional skiving stock problem with . Then alsoholds if E is interpreted as an instance of the one-dimensional cutting stock problem.
Proof. See [4242. ZAK EJ. 2003. The skiving stock problem as a counterpart of the cutting stock problem. International Transactions in Operational Research , 10: 637-650., Theorem 2]. □
Theorem 7. The following assertions hold:
-
Letbe an instance of the one-dimensional cutting stock problem with . If E is a non-IRUP instance then E considered as an instance of the skiving stock problem is a non-IRDP instance, too.
-
Letbe an instance of the one-dimensional skiving stock problem with . If E is a non-IRDP instance then E considered as an instance of the cutting stock problem is a non-IRUP instance, too.
Proof. Let be a non-IRUP instance of the cutting stock problem with . Note that, in this case, also holds due to Lemma 8. Then it is not possible to find an integer solution consisting of cutting patterns. Since all these cutting patterns would have to be trim-less this is equivalent to the non-existence of k (exact) packing patterns. Hence, we have which proves . In an analogous way, the second statement can be proved. □
Based on this important observation and non-IRUP instances from the literature, we obtain the following main result:
Proposition 1.Any instance E of the following families satisfies, i.e., none of the presented instances possesses the IRDP:
-
(a)with , and
-
(b)with , and
-
(c)with , and
-
(d)with , and
-
(e)with , and
Proof. The families (a)-(d) are taken from [3434. RIETZ J, SCHEITHAUER G & TERNO J. 2002. Families of non-IRUP instances of the one-dimensional cutting stock problem. Discrete Applied Mathematics , 121: 229-245., Proposition 3], [3434. RIETZ J, SCHEITHAUER G & TERNO J. 2002. Families of non-IRUP instances of the one-dimensional cutting stock problem. Discrete Applied Mathematics , 121: 229-245., Proposition 6], [3535. RIETZ J, SCHEITHAUER G & TERNO J. 2002. Tighter Bounds for the Gap and Non-IRUP Constructions in the One-dimensional Cutting Stock Problem. Optimization, 51(6): 927-963., Proposition 7], and [3232. RIETZ J. 2003. Untersuchungen zu MIRUP für Vektorpackprobleme. Ph.D. thesis, Technische Universität Dresden., Aussage 19] (in precisely that order) with respect to the cutting stock problem.
The set (e) basically appears in [3232. RIETZ J. 2003. Untersuchungen zu MIRUP für Vektorpackprobleme. Ph.D. thesis, Technische Universität Dresden., Aussage 16], but there is required. By way of exception, we will provide a small part of the proof in order to indicate that, actually, only is sufficient: At first, we obtain
implying that has to hold. On the other hand, we also have
which leads to . Note that is required since, otherwise, the first pattern would contain a negative entry. The rest of the proof follows the ideas published in 3232. RIETZ J. 2003. Untersuchungen zu MIRUP für Vektorpackprobleme. Ph.D. thesis, Technische Universität Dresden. for the cutting stock problem. □
Remark 11. For the sake of completeness, observe that:
-
The instances E(t) from (a) turn out to be equivalent for , see [3232. RIETZ J. 2003. Untersuchungen zu MIRUP für Vektorpackprobleme. Ph.D. thesis, Technische Universität Dresden., Aussage 14].
-
According to Lemma 5, the non-IRDP instances presented in (e) are minimal with respect to the value .
-
All proofs of this subsection (mostly referred to by appropriate literature references) strongly depend on the specific structure of the given instances, either with reference to the particular item lengths li or their availabilities . Although we do not intend to investigate within this article, whether small perturbations of these input data may destroy the key properties to obtain , our first feelings are that the current proofs would have to be rephrased considerably after having (slightly) changed the listed instances.
Obviously, the integrality of is a main ingredient of the proof of Theorem 7. Consequently, the method (to simply use non-IRUP instances of the CSP) cannot be straightforwardly applied to find non-IRDP instances of the skiving stock problem with . Hence, other approaches will become necessary in order to obtain larger gaps. For the cutting stock problem, J. Rietz has proposed several methods to construct larger gaps based on a few given non-IRUP instances [3232. RIETZ J. 2003. Untersuchungen zu MIRUP für Vektorpackprobleme. Ph.D. thesis, Technische Universität Dresden., Sect. 4.5]. As a result of extensive theoretical considerations, he succeeded in finding an instance E with which still represents the largest known gap in the cutting stock context. Due to the expected efforts, at the moment we do not intend to investigate whether these additional approaches can also be transferred to the skiving stock problem or not. However, although not being discussed here, it is likely that similar results can be observed for the SSP, too. Then, any class of non-IRDP instances listed in Section 6, may represent a valuable basis to find non-IRDP instances of the skiving stock problem with . For that reason, an additional class will be introduced and thoroughly discussed in the upcoming subsection.
6.2 A New Construction Principle for Large Gaps of the Divisible Case
The divisible case (where holds for all ) of the skiving stock problem has recently been proved to possess the MIRDP, see 2222. MARTINOVIC J & SCHEITHAUER G. 2016. Integer Rounding and Modified Integer Rounding for the Skiving Stock Problem. Discrete Optimization, 21: 118-130.), (2525. MARTINOVIC J & SCHEITHAUER G. 2017. An Upper Bound of ∆(E) < 3/2 for Skiving Stock Instances of the Divisible Case. Discrete Applied Mathematics, 229: 161-167.. Moreover, in that paper, a construction principle is presented that leads to a maximum gap of . By further manipulations of the resulting instances slightly larger gaps can be obtained. In this subsection we present a new construction method to obtain non-IRDP instances of the divisible case. Contrary to 2222. MARTINOVIC J & SCHEITHAUER G. 2016. Integer Rounding and Modified Integer Rounding for the Skiving Stock Problem. Discrete Optimization, 21: 118-130., this approach
-
possesses a less complex construction (only two parameters determine the whole instance, whereas four quantities are needed for the strategy in [2222. MARTINOVIC J & SCHEITHAUER G. 2016. Integer Rounding and Modified Integer Rounding for the Skiving Stock Problem. Discrete Optimization, 21: 118-130., Theorem 14]),
-
directly leads to a gap , and
-
only requires a fixed number of item types (compared to for the class presented in 2222. MARTINOVIC J & SCHEITHAUER G. 2016. Integer Rounding and Modified Integer Rounding for the Skiving Stock Problem. Discrete Optimization, 21: 118-130.),
so that it exhibits significant advantages in comparison with the previous method. Moreover, this procedure also provides gaps arbitrarily close to (but strictly less than) 22/21 if further items are allowed to be added.
Our new construction is based on the following simple observation.
Lemma 9.Letbe relatively prime with. Then
holds for.
Proof. For the sake of contradiction, we assume that is a common prime factor of ξ1 and ξ3. Then also has to be an integer multiple of d. But, on the other hand, we have
which gives the contradiction. The same proof can be applied to ξ2 instead of ξ1. □
Now let satisfy the conditions of the previous lemma, and let . We claim that the instance
possesses a gap larger than one. Obviously, the defined instance belongs to the divisible case.
Hence, the optimal objective value of its continuous relaxation is given by
Note that the second summand is always positive for the feasible choices of (ξ1, ξ2). Hence, it suffices to show that holds in order to prove that E(ξ1, ξ2) represents a non-IRDP instance.
Theorem 8. Let
be defined as in (8). Then the following assertions hold:
-
1. The inequality
-
holds for allwith .
-
2. The gap of E results to
-
i.e., E is a non-IRDP instance.
Proof. Both statements are proved by contradiction. In the first part, the main idea is to show that any counterexample would have to satisfy , but a deeper investigation based on number theory reveals that none of these cases can occur. Then, the second statement is a straightforward consequence of the first one. The full details can be found in the Appendix APPENDIX: PROOF OF THEOREM 8 Let E:=E(ξ1,ξ2) be defined as in (8). 1. For the sake of contradiction, we assume that there is a pattern a∈P*(E) with a≤b satisfying 1 ≤ a 1 ξ 1 + a 2 ξ 2 + a 3 ξ 3 ≤ 1 + ξ 1 ξ 2 − ( ξ 1 + ξ 2 ) ξ 1 ξ 2 ( ξ 1 ξ 2 + 1 ) . (15) Part 1: Finding a necessary condition for (15): By multiplying (15) with the common denominator ξ1ξ2(ξ1ξ2+1) and rearranging the terms, we obtain 1 ≤ a 1 ξ 1 + a 2 ξ 2 + a 3 ξ 3 ≤ 1 + ξ 1 ξ 2 − ( ξ 1 + ξ 2 ) ξ 1 ξ 2 ( ξ 1 ξ 2 + 1 ) ⇔ { ξ 1 ξ 2 ( ξ 1 ξ 2 + 1 ) ≤ a 1 ξ 2 ( ξ 1 ξ 2 + 1 ) + a 2 ξ 1 ( ξ 1 ξ 2 + 1 ) + a 3 ξ 1 ξ 2 ≤ ξ 1 ξ 2 ( ξ 1 ξ 2 + 1 ) + ξ 1 ξ 2 − ξ 1 − ξ 2 ⇔ { ξ 1 ξ 2 − a 1 ξ 2 − a 2 ξ 1 ≤ a 1 ξ 1 ξ 2 2 + a 2 ξ 1 2 ξ 2 + a 3 ξ 1 ξ 2 − ( ξ 1 ξ 2 ) 2 ≤ 2 ξ 1 ξ 2 − ξ 1 − ξ 2 − a 1 ξ 2 − a 2 ξ 1 ⇔ { − a 1 ξ 2 + ( ξ 2 − a 2 ) ξ 1 ≤ ξ 1 ξ 2 ( a 1 ξ 2 + a 2 ξ 1 + a 3 − ξ 1 ξ 2 ) ≤ ( ξ 1 − a 1 ) ξ 2 + ( ξ 2 − a 2 ) ξ 1 − ξ 1 − ξ 2 ⇔ { − a 1 ξ 2 + ( ξ 2 − a 2 ) ξ 1 ︸ = : β l ≤ ξ 1 ξ 2 ( a 1 ξ 2 − ( ξ 2 − a 2 ) ξ 1 + a 3 ) ≤ ( ξ 1 − a 1 − 1 ) ξ 2 + ( ξ 2 − a 2 − 1 ) ξ 1 ︸ : = β u (16) Now we aim at finding a lower bound for βl and an upper bound for βu in order to derive a necessary condition for the components a 1, a 2, a 3 of the considered pattern a∈P*(E) . At first, note that we have β u = ( ξ 1 − a 1 − 1 ) ξ 2 + ( ξ 2 − a 2 − 1 ) ξ 1 < 2 ξ 1 ξ 2 due to a1≥0 and a2≥0 . On the other hand, we also obtain β l = − a 1 ξ 2 + ( ξ 2 − a 2 ) ξ 1 ≥ − ( ξ 1 − 1 ) ξ 2 + ξ 1 = − ξ 1 ξ 2 + ξ 1 + ξ 2 > − ξ 1 ξ 2 due to a1≤b1=ξ1−1 and a2≤b2=ξ2−1 . Altogether, these estimates imply that − ξ 1 ξ 2 < ξ 1 ξ 2 ( a 1 ξ 2 − ( ξ 2 − a 2 ) ξ 1 + a 3 ) < 2 ξ 1 ξ 2 or, equivalently, − 1 < a 1 ξ 2 − ( ξ 2 − a 2 ) ξ 1 + a 3 < 2 (17) is a necessary condition for (15). Part 2: Case Studies: Note that (17) is equivalent to a1ξ2−(ξ2−a2)ξ1+a3∈{0,1} . (a) Case 1:a1ξ2−(ξ2−a2)ξ1+a3=0 In this case, the first inequality of (16) leads to −a1ξ2+(ξ2−a2)ξ1≤0 implying that 0 = a 1 ξ 2 − ( ξ 2 − a 2 ) ξ 1 + a 3 ≥ a 3 ≥ 0 has to hold. Consequently, we have a3=0 and a1ξ2=(ξ2−a2)ξ1 . Due to a1∈ℤ+ , we further have a 1 = ( ξ 2 − a 2 ) ξ 1 ξ 1 ∈ ℤ + ⇔ ( ξ 2 − a 2 ) ξ 1 ≡ 0 mod ξ 2 . (18) But then, note that 0 ≡ ( ξ 2 − a 2 ) ξ 1 ≡ 0 − a 2 ξ 1 ≡ − a 2 ξ 1 mod ξ 2 has to hold which is true if and only if a2≡0modξ2 due to the fact that ξ1 and ξ2 are relatively prime. Since we have 0≤a2≤b2=ξ2−1 the only possible choice is a2=0 . But this implies a1=ξ1 by means of the left side of (18) which gives the contradiction since a1≤b1=ξ1−1 has to be satisfied. (b) Case 2:a1ξ2−(ξ2−a2)ξ1+a3=1 In this case, the second inequality of (16) leads to ξ 1 ξ 2 ≤ 2 ξ 1 ξ 2 − ξ 1 − ξ 2 − a 1 ξ 2 − a 2 ξ 1 ⇔ a 1 ξ 2 + ξ 1 + ξ 2 ≤ ( ξ 2 − a 2 ) ξ 1 implying that 1 = a 3 + a 1 ξ 2 − ( ξ 2 − a 2 ) ξ 1 ︸ ≥ a 1 ξ 2 + ξ 1 + ξ 2 ≤ a 3 − ξ 1 − ξ 2 ≤ 1 has to hold due to a3≤b3=ξ1+ξ2+1 . Consequently, we have a3=ξ1+ξ2+1 and, due to the assumption of this case, a1ξ2=(ξ2−a2)ξ1−ξ1−ξ2 . According to a1∈ℤ+ , we further have a 1 = ( ξ 2 − a 2 ) ξ 1 − ξ 1 − ξ 2 ξ 2 ∈ ℤ + ⇔ ( ξ 2 − a 2 ) ξ 1 − ξ 1 − ξ 2 ≡ 0 mod ξ 2 . (19) But then, note that 0 ≡ ( ξ 2 − a 2 ) ξ 1 − ξ 1 − ξ 2 ≡ − a 2 ξ 1 − ξ 1 ≡ − ξ 1 ( a 2 + 1 ) mod ξ 2 has to hold which is true if and only if a2+1≡0modξ2 due to the fact that ξ1 and ξ2 are relatively prime. Since we have 0≤a2≤b2=ξ2−1 the only possible choice is a2=ξ2−1 . But this implies a1=−1 by means of the left side of (19) which gives the contradiction since 0≤a1 has to be satisfied. Consequently, there is no pattern that satisfies the necessary condition (17) which gives the contradiction to the initial assumption. 2. For the sake of contradiction, we assume that z*(E)=2 is true. Hence, we can find two patterns a1,a2∈P*(E) with a1+a2≤b . Due to the first part of this theorem, we have l ⊤ a j > 1 + ξ 1 ξ 2 − ( ξ 1 + ξ 2 ) ξ 1 ξ 2 ( ξ 1 ξ 2 + 1 ) for j∈{1,2} . But then, also 2 + ξ 1 ξ 2 − ( ξ 1 + ξ 2 ) ξ 1 ξ 2 ( ξ 1 ξ 2 + 1 ) = l ⊤ b ≥ l ⊤ a 1 + l ⊤ a 2 > 2 + 2 ⋅ ξ 1 ξ 2 − ( ξ 1 + ξ 2 ) ξ 1 ξ 2 ( ξ 1 ξ 2 + 1 ) has to be satisfied which is not possible. Hence, we have z*(E)≤1 and, due to l⊥b≥L=1,z*(E)=1 . Consequently, the gap of the instance E can be computed as in (9) and the proof is complete. □ . □
Note that for and we obtain the instance
which is equivalent to the instance E(2) of [2222. MARTINOVIC J & SCHEITHAUER G. 2016. Integer Rounding and Modified Integer Rounding for the Skiving Stock Problem. Discrete Optimization, 21: 118-130., Theorem 14]. Hence, the method that was presented here can be understood as a generalization of the case in the aforementioned theorem. But then, the question arises whether it is possible to achieve a larger gap than (from [2222. MARTINOVIC J & SCHEITHAUER G. 2016. Integer Rounding and Modified Integer Rounding for the Skiving Stock Problem. Discrete Optimization, 21: 118-130., Theorem 15]) with this new approach.
Proposition 2. The equation
holds. The unique solution is given byand.
Proof. At first, observe that and , actually, lead to the objective value 5/156. Furthermore, we have
due to
where the latter is certainly true. Consequently, if (ξ1, ξ2) is a solution of the considered maximization problem, has to hold due to (10). But then, we have which is equivalent to due to the integrality of the left hand side. The only remaining pairs (ξ1, ξ2) with relatively prime and are given in Table 1. Obviously, we cannot obtain an objective value larger than 5/156. Thus, the unique solution is given by and . □
Objective values for the remaining pairs (ξ1, ξ2), where the crossed cells are not feasible. The cell (ξ1, ξ2) = (3, 4) represents the maximum value.
As a consequence of this proposition, the largest gap that can be constructed with the presented approach results to for the choice which corresponds to the instance
Note that this gap is larger than all the gaps that can be obtained by [2222. MARTINOVIC J & SCHEITHAUER G. 2016. Integer Rounding and Modified Integer Rounding for the Skiving Stock Problem. Discrete Optimization, 21: 118-130., Theorem 14]. This gives hope that by adding some sufficiently small item lengths (that do not influence ), gaps larger than or equal to 22/21 (as in [2222. MARTINOVIC J & SCHEITHAUER G. 2016. Integer Rounding and Modified Integer Rounding for the Skiving Stock Problem. Discrete Optimization, 21: 118-130., Corollary 16]) can be obtained. Hence, the remainder of this subsection will deal with the computation of
for a given instance E(ξ1, ξ2) as in (8), since then we can add items of total length less than
without changing . Note that, by this procedure, z * (E) and ∆(E) will increase. To this end, we start with the following lemmas.
Lemma 10. Let be relatively prime. Then there exists
with ξ1|ψ and.
Proof. It suffices to show that there exists with
since, then, ξ1|νξ1 and are clear by construction. Therefore, remember that is true which implies that ξ1 is invertible in the set of residue classes modulo ξ2, i.e., in . Hence, we can find with and . Setting , we obtain an element of the set such that
is satisfied which completes the proof. □
Lemma 11. Let be relatively prime. Then there exists a solution of
withandfor.
Proof. Due to the previous lemma, we can find with ξ1|ψ and . We define
and claim that this is a feasible solution of (12). Indeed, we have:
-
1. Equation (12) is satisfied due to
-
2. At first, note that is true since we have
-
Additionally, the definition of a 1 meets the box constraints due to
-
where has been used, and
-
where the latter is equivalent to according to the integrality of a 1.
-
3. At first, note that is true since we have ξ1|ψ. Additionally, the definition of a 2 meets the box constraints due to and
Now we can state the main result of this consideration.
Proposition 3. Let be relatively prime. Then the minimum in (11) is given by
Proof. Note that, due to the first part of Theorem 8, we already have
Hence, it suffices to find a feasible triple (a 1, a 2, a 3) that attains this lower bound. To this end, we claim that there exists such a triple with , i.e., we claim that the equation
has a solution with and for . Multiplying with the common denominator and rearranging the terms lead to the equivalent formulations
where has been used in the last line. Then, the last equation can be solved due to the previous lemma. Hence equality (13) is true. □
Consequently, we obtain
Hence, by adding sufficiently small items, we can construct gaps arbitrarily close to
As a last contribution of this subsection, we aim at computing the maximum gap that can be (approximately) achieved in this way.
Proposition 4. The equation
holds. The unique solution is given byand.
Proof. At first, observe that and , actually, lead to the objective value 1/21. Furthermore, we have
due to
where the latter is certainly true, since is satisfied. Consequently, if (ξ1, ξ2) is a solution of the considered maximization problem, has to hold due to (14). This is equivalent to . The only remaining pairs (ξ1, ξ2) with relatively prime and are given in Table 2. Obviously, we cannot obtain an objective value larger than 1/21. Thus, the unique solution is given by and .
Objective values for the remaining pairs (ξ1, ξ2), where the crossed cells are not feasible. The cell represents the maximum value.
Unfortunately, this approach does not provide gaps of the divisible case greater than or equal to 22/21 and, hence, does not improve our max-gap considerations of [2222. MARTINOVIC J & SCHEITHAUER G. 2016. Integer Rounding and Modified Integer Rounding for the Skiving Stock Problem. Discrete Optimization, 21: 118-130., Corollary 15]. Nevertheless, we have found a new construction principle for non-IRDP instances of the divisible case. As we have stated, this method can be interpreted as a generalization of the case in [2222. MARTINOVIC J & SCHEITHAUER G. 2016. Integer Rounding and Modified Integer Rounding for the Skiving Stock Problem. Discrete Optimization, 21: 118-130., Theorem 14]. Additionally, one of the new instances has a gap of 1 + 5/156 without the addition of further small items which surpassed the previous maximum of 1 + 1/42. Altogether, as mentioned earlier, note that any kind of non-IRDP instance can be valuable when looking for larger gaps (maybe in the sense of constructions similar to those of Rietz 3232. RIETZ J. 2003. Untersuchungen zu MIRUP für Vektorpackprobleme. Ph.D. thesis, Technische Universität Dresden.), so that this new approach not only provides some interesting results on non-IRDP instances and their corresponding gaps, but may also be relevant for further scientific research in that particular field.
7 CONCLUSIONS
In this paper we reported on the skiving stock problem with special respect to the quality of its continuous relaxation. At first, we showed how upper bounds for the gap of arbitrary instances can be found by means of the concept of residual instances. In particular, we improved the best known upper bound to (at least) , and provided additional upper bounds that make use of all problem-specific input data. In the remainder we focused on IRDP and non-IRDP instances and were able to apply the first-fit decreasing heuristic in order to prove for two new classes of instances. By investigating the relationships between the cutting stock problem and the skiving stock problem, we presented several construction principles to obtain non-IRDP instances that do not belong to the divisible case. In a final step, we introduced a new method to construct large gaps of the skiving stock problem and obtained an alternative way to build instances with gaps arbitrarily close to 22/21, which represents the currently best known value for the divisible case.
One of the main parts of our future research is given by improving the upper bound for the gap of the skiving stock problem, since for the related cutting stock problem estimates like 𝒪(m/4) (see 3535. RIETZ J, SCHEITHAUER G & TERNO J. 2002. Tighter Bounds for the Gap and Non-IRUP Constructions in the One-dimensional Cutting Stock Problem. Optimization, 51(6): 927-963.) are already available. Additionally, we will focus on proving the IRDP or the MIRDP for further classes of instances, and the development of other construction principles that may lead to larger gaps. Alternatively, also the investigation of asymptotic polynomial time approximation schemes (APTAS) for the dual bin packing or the skiving stock problem, maybe based on the observations in 66. CINTRA G, MIYAZAWA FK, WAKABAYASHI Y & XAVIER EC. 2007. A note on the approximability of cutting stock problems. European Journal on Operations Research, 183: 1328-1332.), (1414. JANSEN K & SOLIS-OBA R. 2003. An asymptotic fully polynomial time approximation scheme for bin covering. Theoretical Computer Science, 306: 543-551., could be of interest to obtain approximate solutions of reasonable quality.
REFERENCES
-
1ASSMANN SF, JOHNSON DS, KLEITMAN DJ & LEUNG JYT. 1984. On a dual version of the one-dimensional Bin Packing Problem. Journal of Algorithms, 5: 502-525.
-
2BAR-NOY A, LADNER RE & TAMIR T. 2007. Windows Scheduling As a Restricted Version of Bin Packing. ACM Transactions on Algorithms, 3(3): article 28.
-
3BAUM S & TROTTER LE. 1981. Integer rounding for polymatroid and branching optimization problems. SIAM Journal of Algebraic and Discrete Methods, 2: 416-425.
-
4CAPRARA A, DELL’AMICO M, DIAZ-DIAZ JC, IORI M & RIZZI R. 2015. Friendly bin packing instances without Integer Round-up Property. Mathematical Programming, 150: 5-17.
-
5CHEN Y, SONG X, OUELHADJ D & CUI Y. 2019. A heuristic for the skiving and cutting stock problem in paper and plastic film industries. International Transactions in Operational Research, 26(1): 157-179.
-
6CINTRA G, MIYAZAWA FK, WAKABAYASHI Y & XAVIER EC. 2007. A note on the approximability of cutting stock problems. European Journal on Operations Research, 183: 1328-1332.
-
7COFFMAN JR EG, GAREY MR & JOHNSON DS. 1987. Bin packing with divisible item sizes. Journal of Complexity, 3: 406-428.
-
8DELORME M, IORI M & MARTELLO S. 2016. Bin Packing and Cutting Stock Problems: Mathematical Models and Exact Algorithms. European Journal of Operational Research, 255: 1-20.
-
9EISENBRAND F & WEISMANTEL R. 2017, Proximity results and faster algorithms for Integer Programming using the Steinitz Lemma. Available online: https://arxiv.org/abs/1707.00481
» https://arxiv.org/abs/1707.00481 -
10FIELDHOUSE M. 1990. The duality gap in trim problems. SICUP-Bulletin, 5: 4-5.
-
11GARFINKEL R & NEMHAUSER GL. 1972. Integer Programming. Wiley, New York.
-
12GILMORE PC & GOMORY RE. 1961. A Linear programming approach to the cutting-stock problem (Part I). Operations Research, 9: 849-859.
-
13GODINHO MT, GOUVEIA L & PESNEAU P. 2011. On a Time-Dependent Formulation and an Updated Classification of ATSP Formulations. In: MAHJOUB R (Ed.), Progress in Combinatorial Optimization, Wiley.
-
14JANSEN K & SOLIS-OBA R. 2003. An asymptotic fully polynomial time approximation scheme for bin covering. Theoretical Computer Science, 306: 543-551.
-
15JOHNSON MP, RENNICK C & ZAK EJ. 1997. Skiving addition to the cutting stock problem in the paper industry. SIAM Review, 39(3): 472-483.
-
16KANTOROVICH LV. 1960. Mathematical methods of organising and planning production. Management Science, 6: 366-422.
-
17LABBÉ M, LAPORTE G & MARTELLO S. 1995. An exact algorithm for the dual bin packing problem. Operations Research Letters, 17: 9-18.
-
18MARCOTTE O. 1983. Topics in combinatorial packing and covering. Technical report, No.568, Cornell University.
-
19MARCOTTE O. 1985. The cutting stock problem and integer rounding. Mathematical Programming , 33(1): 82-92.
-
20MARTINOVIC J, JORSWIECK E, SCHEITHAUER G & FISCHER A. 2017. Integer Linear Programming Formulations for Cognitive Radio Resource Allocation. IEEE Wireless Communication Letters, 6(4): 494-497.
-
21MARTINOVIC J & SCHEITHAUER G. 2016. Integer linear programming models for the skiving stock problem. European Journal of Operational Research , 251(2): 356-368.
-
22MARTINOVIC J & SCHEITHAUER G. 2016. Integer Rounding and Modified Integer Rounding for the Skiving Stock Problem. Discrete Optimization, 21: 118-130.
-
23MARTINOVIC J & SCHEITHAUER G. 2016. The Proper Relaxation and the Proper Gap of the Skiving Stock Problem. Mathematical Methods of Operations Research , 84(3): 527-548.
-
24MARTINOVIC J & SCHEITHAUER G. 2017. LP-based Relaxations of the Skiving Stock Problem - Improved Upper Bounds for the Gap. Operations Research Proceedings 2015, pp. 49-54.
-
25MARTINOVIC J & SCHEITHAUER G. 2017. An Upper Bound of ∆(E) < 3/2 for Skiving Stock Instances of the Divisible Case. Discrete Applied Mathematics, 229: 161-167.
-
26MARTINOVIC J & SCHEITHAUER G. 2018. An Improved Upper Bound for the Gap of Skiving Stock Instances of the Divisible Case. Operations Research Proceedings 2017, pp. 179-184.
-
27MARTINOVIC J, SCHEITHAUER G & VALÉRIO DE CARVALHO JM. 2018. A Comparative Study of the Arcflow Model and the One-Cut Model for one-dimensional Cutting Stock Problems. European Journal of Operational Research , 266(2): 458-471.
-
28MILLER CE, TUCKER AW & ZEMLIN RA. 1960. Integer Programming Formulation of Traveling Salesman Problems. Journal of the ACM, 7(4): 326-329.
-
29NEMHAUSER GL & WOLSEY LA. 1988. Integer and Combinatorial Optimization. Wiley, New York .
-
30NICA V. 1994. A General counterxample to the Integer Round-Up property, working paper, Department of Economic Cybernetics, Academy of Economic Studies, Bucharest.
-
31PEETERS M & DEGRAEVE Z. 2006. Branch-and-price algorithms for the dual bin packing and maximum cardinality bin packing problem. European Journal of Operational Research , 170(2): 416-439.
-
32RIETZ J. 2003. Untersuchungen zu MIRUP für Vektorpackprobleme. Ph.D. thesis, Technische Universität Dresden.
-
33RIETZ J & DEMPE S. 2008. Large gaps in one-dimensional cutting stock problems. Discrete Applied Mathematics , 156(10): 1929-1935.
-
34RIETZ J, SCHEITHAUER G & TERNO J. 2002. Families of non-IRUP instances of the one-dimensional cutting stock problem. Discrete Applied Mathematics , 121: 229-245.
-
35RIETZ J, SCHEITHAUER G & TERNO J. 2002. Tighter Bounds for the Gap and Non-IRUP Constructions in the One-dimensional Cutting Stock Problem. Optimization, 51(6): 927-963.
-
36ROBERTI R & TOTH P. 2012. Models and algorithms for the Asymmetric Traveling Salesman Problem: an experimental comparison. EURO Journal on Transportation and Logistics, 1(1-2): 113-133.
-
37SCHEITHAUER G. 2018. Introduction to Cutting and Packing Optimization - Problems, Modeling Approaches, Solution Methods. International Series in Operations Research & Management Science 263, Springer, 1 ed.
-
38SHERALI HD, SARIN SC & TSAI PF. 2006. A class of lifted path and flow-based formulations for the asymmetric traveling salesman problem with and without precedence constraints. Discrete Optimization , 3(1): 20-32.
-
39TRAGOS EZ, ZEADALLY S, FRAGKIADAKIS AG & SIRIS VA. 2013. Spectrum Assignment in Cognitive Radio Networks: A Comprehensive Survey. IEEE Communications Surveys & Tutorials, 15(3): 1108-1135.
-
40VALÉRIO DE CARVALHO JM. 2002. Lp models for bin packing and cutting stock problems. European Journal of Operations Research , 141(2): 253-273.
-
41WÄSCHER G, HAUSSNER H & SCHUMANN H. 2007. An improved typology of cutting and packing problems. European Journal of Operational Research , 183: 1109-1130.
-
42ZAK EJ. 2003. The skiving stock problem as a counterpart of the cutting stock problem. International Transactions in Operational Research , 10: 637-650.
APPENDIX: PROOF OF THEOREM 6
We consider the decomposition of point (ii) in Remark 8 and apply Phase I of Algorithm 1 on E 1 and E 2 separately. Let denote the number of bins of subinstance E i , then we either have or , where R i (q i ) denotes the remaining capacity of the last bin of instance E i .
-
Case 1: The equality holds.
-
In this case, both instances possess only bins that are filled exactly, i.e., we have for . Hence we obtain leading to
-
i.e., the IRDP of E.
-
Case 2: There is exactly one index with .
-
Without loss of generality we assume . Then we have , and due to the observations in the proof of Theorem 5 we further obtain
-
Combining these feasible solutions of the subinstances results to implying that
-
has to hold, i.e., E has the IRDP.
-
Case 3: The inequalities and hold.
-
As in the previous case, the proof of Theorem 5 leads to
-
for . Now there are again two cases
-
Subcase 3.1:
-
Let
-
be satisfied. Then a combination of the feasible solutions of the two subinstances leads to . Thus we obtain
-
i.e. the IRDP of E.
-
Subcase 3.2:
-
be satisfied. By joining the items of the bins q 1 from E 1 and q 2 from E 2 we obtain an additional filled bin. A combination of all bins leads to , implying that
-
i.e., E has the IRDP. □
APPENDIX: PROOF OF THEOREM 8
Let be defined as in (8).
-
1. For the sake of contradiction, we assume that there is a pattern with satisfying
-
Part 1: Finding a necessary condition for (15):
-
By multiplying (15) with the common denominator and rearranging the terms, we obtain
-
Now we aim at finding a lower bound for βl and an upper bound for βu in order to derive a necessary condition for the components a 1, a 2, a 3 of the considered pattern . At first, note that we have
-
due to and . On the other hand, we also obtain
-
due to and . Altogether, these estimates imply that
-
or, equivalently,
-
is a necessary condition for (15).
-
Part 2: Case Studies:
-
Note that (17) is equivalent to .
-
(a) Case 1:
-
In this case, the first inequality of (16) leads to implying that
-
has to hold. Consequently, we have and . Due to , we further have
-
But then, note that
-
has to hold which is true if and only if due to the fact that ξ1 and ξ2 are relatively prime. Since we have the only possible choice is . But this implies by means of the left side of (18) which gives the contradiction since has to be satisfied.
-
(b) Case 2:
-
In this case, the second inequality of (16) leads to
-
implying that
-
has to hold due to . Consequently, we have and, due to the assumption of this case, . According to , we further have
-
But then, note that
-
has to hold which is true if and only if due to the fact that ξ1 and ξ2 are relatively prime. Since we have the only possible choice is . But this implies by means of the left side of (19) which gives the contradiction since has to be satisfied.
-
Consequently, there is no pattern that satisfies the necessary condition (17) which gives the contradiction to the initial assumption.
-
2. For the sake of contradiction, we assume that is true. Hence, we can find two patterns with . Due to the first part of this theorem, we have
-
for . But then, also
-
has to be satisfied which is not possible. Hence, we have and, due to . Consequently, the gap of the instance E can be computed as in (9) and the proof is complete. □
Publication Dates
-
Publication in this collection
09 May 2019 -
Date of issue
Jan-Apr 2019
History
-
Received
25 July 2018 -
Accepted
30 Jan 2019