Introdução ao controle de sistemas não-holonômicos

Introdução ao controle de sistemas não-holonômicos

Luiz C. Figueiredo^I; Fabio G. Jota^II

^IDepartamento de Engenharia Elétrica - UNILESTE-MG, Av. Tancredo Neves 3500, CEP - 35170-056, Cel. Fabriciano, MG, Brasil, [e-mail]

^IIDepartamento de Engenharia Eletrônica - UFMG, Av. Antonio Carlos 6627, CEP - 31270-901, Belo Horizonte, MG, Brasil, [e-mail]

RESUMO

Este artigo tem como objetivo caracterizar e apresentar os recentes desenvolvimentos no controle de sistemas não-holonômicos, destacando robôs móveis com restrições Pfaffianas, propiciando um panorama geral para quem esta iniciando na área. As principais ferramentas de modelagem, análise, planejamento do movimento, seguimento de trajetórias e estabilização num ponto de equilíbrio são apresentadas. O desenvolvimento de novas técnicas de análise e síntese de controladores baseada em controle não-linear, controle híbrido, controle variante no tempo, e controle geométrico tem possibilitado o controle de sistemas não-holonômicos. São dados exemplos de aplicação restritos a simulação do controle de um robô móvel com acionamento diferencial. São apresentadas comparações entre algumas técnicas de controle e perspectivas para a área.

Palavras-chave: Sistemas não-holonômicos, controle não-linear, controle geométrico, sistemas de controle.

ABSTRACT

The objective of this paper is to present recent developments in nonholonomic control systems, mainly mobile robots with Pfaffians constraints, so as to give an overview to the beginners in the area. The main tools used to model, to analyze, to make motion planning and trajectory tracking and to guarantee stabilization in an equilibrium point are presented. The development of new tools in controller analysis and design based in nonlinear, hybrid, time varying, and geometric control made possible the control of nonholonomic systems. Application examples, restricted to simulation of differential driven mobile robot (unicycle) control, are given. A comparative analysis between some control techniques and perspectives to the area are also presented.

Keyword: Nonholonomic systems, nonlinear control, geometric control, control systems.

1 INTRODUÇÃO

Este trabalho tem como objetivo apresentar os conceitos básicos da teoria de sistemas não-holonômicos, bem como mostrar alguns recentes desenvolvimentos e tendências da pesquisa sobre o tema, destacando robôs móveis com restrições Pfaffianas, propiciando um panorama geral para quem esta iniciando na área. Para tal é necessário se ter uma base matemática, ferramentas de análise e projeto, métodos de controle em malha aberta e geração de trajetórias de estado, métodos de controle em malha fechada para estabilização em uma trajetória ou em um ponto de equilíbrio. Inicia-se com uma apresentação dos conceitos de geometria diferencial utilizada na análise e classificação de restrições, como ferramenta de transformação de modelos, e método de geração de sinais de deslocamento (ex.: colchete de Lie). Apresenta-se uma distinção entre estabilização numa trajetória e num ponto de equilíbrio, e alguns exemplos de controladores utilizando técnicas avançadas de controle. Para facilitar o entendimento inicial, sistemas dinâmicos não-holonômicos e ferramentas de controle mais avançadas (adaptativo, robusto, etc.) não são descritas.

O termo holonômico é atribuido a Hertz (Arnol'd and (Eds.), 1994) e significa "universal", "integral", "integrável" ( literalmente: holo = o todo, conjunto, totalidade - nomia = lei). Portanto, sistemas não-holonômicos podem ser interpretados como sistemas não integráveis.

A abordagem matemática a este tipo de problema é realizada através de ferramentas da geometria diferencial. O desenvolvimento sistemático da teoria iniciou-se há mais de 150 anos, baseado numa série de artigos clássicos sobre a mecânica não-holonômica de matemáticos e físicos tais como: Hertz, Voss, Hölder, Chaplygin, Appel, Rooth, Woronets, Korteweg, Carathéodory, Horac, Voltera, dentre outros. Apesar disto, apenas recentemente (Kolmanovsky and McClamroch, 1995) se iniciou o estudo de problemas de controle para tais sistemas.

Definem-se como não-holonômicos sistemas com dimensão finita onde algum tipo de restrição é imposta a um ou mais estados do sistema. Estas limitações podem ser provocadas pela conservação do momento angular, condições impostas pela impossibilidade de deslocar em uma ou mais direções, como resultado da imposição de restrições durante o projeto do sistema de controle, pelo fato de o sistema não ter atuadores em todas as direções do espaço do problema, e em várias outras situações (Murray et al., 1994). Wen (Wen, 1996) indica três classes de sistemas onde restrições não-holonômicas aparecem:

• Restrição de não-deslize. A condição de não-deslizamento ou de rolamento puro significa que a velocidade linear no ponto de contato é zero. Esta restrição é não-integrável, isto é, não redutível a uma restrição de posição, e portanto é não-holonômica.

• Conservação do momento angular.

• Sistemas mecânicos subatuados. Sistemas nos quais a dimensão do espaço de configurações excede o espaço das entradas de controle.

Exemplos de sistemas não-holonômicos e da geração de trajetórias para os mesmos, em especial, para a análise do problema da queda de uma gata (sistema com corpos rígidos acoplados) são abordados em (Fernandes et al., 1994). Este problema é particularmente interessante porque se sabe da mecânica clássica que o momento angular de uma gata em queda é conservado, então como uma gata em queda pode mudar sua orientação sem violar a conservação do momento angular? A análise deste problema utilizando a teoria de aproximação de Ritz leva ao desenvolvimento de um algoritmo numérico para a determinação de soluções quase-ótimas (Fernandes et al., 1994).

Sistemas não-holonômicos formam uma classe com características especiais: apesar de seus movimentos serem limitados, os mesmos podem atingir qualquer configuração no espaço onde estão definidos (quando controláveis e atingíveis); infelizmente as leis de controle para estabilização de sistemas não-holonômicos não são fáceis de serem geradas; há necessidade de emprego de ferramentas matemáticas mais elaboradas para análise e projeto (geometria diferencial e controle não-linear ou linear variante no tempo).

A consideração de restrições ao movimento melhora consideravelmente o controle de sistemas não-holonômicos possibilitando o projeto de controladores multivariáveis exponencialmente estáveis de forma integrada. O desafio para análise e síntese de controladores para sistemas deste tipo tem propiciado o desenvolvimento da teoria de controle não-linear. Técnicas de otimização e controle geométrico empregando transformações de coordenadas (transformações lineares e não-lineares) e sinais variantes no tempo ou descontínuos são utilizadas para a geração de trajetórias e projeto de controladores em malha aberta. Em malha fechada destacam-se: controle adaptativo, robusto, inteligência artificial, linearização por realimentação de estados e das saídas empregando sinais contínuos variantes no tempo ou descontínuos, e técnicas de controle híbrido. As principais técnicas de controle empregam funções de Lyapunov, associada a um método para gerar as leis de controle: integrador de um passo atrás (backstepping), método direto, método inverso, métodos matemáticos, métodos utilizando a física do processo, etc. Segue uma breve revisão bibliográfica sobre pesquisas mais significativas na área.

• Tutoriais: O trabalho que serve como tutorial para iniciantes no controle de sistemas não-holonômicos foi desenvolvido por Kolmanovsky and McClamroch (1995). Apresenta de forma clara e acessível os estágios de desenvolvimento da teoria indicando modelos, técnicas de controle em malha aberta e fechada e métodos de planejamento de trajetórias. Avanços no controle por realimentação variante no tempo são apresentados por Morin and Samson (2000b). Uma visão geral sobre o problema da estabilização de veículos autônomos, indicando problemas em aberto e tendências é apresentado em Aguiar and Pascoal (1999), onde se destaca a necessidade do estudo de incertezas no modelo e o desenvolvimento de controladores robustos, principalmente para veículos marinhos.

• Planejamento de trajetórias: Métodos de planejamento de trajetórias usando geometria diferencial foram propostos por Sussmann (1991), Bushnell et al. (1994), e Sussmann (1993). A utilização de sinais senoidais no planejamento é explorada em Sekhavat and Laumond (1998), e Murray and Sastry (1993). Métodos de deslocamento em malha aberta usando senóides e, em alguns casos, transformações não-lineares são apresentados em Bushnell et al. (1994), Tilbury et al. (1993), Tilbury and Chelouah (1993) e Hunt et al. (1996). A exploração do colchete de Lie para planejamento do movimento é apresentada em Lafferriere and Sussmann (1991). O uso de técnicas de controle ótimo são apresentadas em Sussmann (1992). A incorporação da dinâmica dos sensores no planejamento do movimento é destacada em Shkel and Lumelsky (1997). Wen (1996) apresenta como principais algoritmos de planejamento de trajetória os métodos de deslocamento com entradas cíclicas, métodos baseados em controle ótimo, e os métodos iterativos no espaço de trajetórias. O planejamento de trajetória evitando obstáculos é tratado em Laumond et al. (1994), Latombe (1993), Divelbiss and Wen (1997) e Mirtich and Canny (1992). Um sistema de planejamento e controle totalmente em tempo real é proposto por Lizarralde and Wen (1996). Sistemas não-holonômicos que não satisfazem à condição ideal de restrição de velocidade, isto é, podem apresentar deslizes laterais, são estudados em profundidade em D'Andréa-Novel et al. (1995). Um modelo particular de controle de sistemas não-holonômicos aplicados ao controle de uma bicicleta é apresentado no trabalho de Getz (Getz, 1994; Getz and Marsden, 1995).

• Rastreamento de trajetórias: O rastreamento de trajetórias para sistemas não-holonômicos tem sido buscado por inúmeros pesquisadores. O problema da estabilização em uma trajetória é mais fácil de ser resolvido do que o da estabilização em um ponto (Walsh et al., 1994) desde que seja possível calcular previamente uma trajetória que satisfaça as restrições. Métodos simples utilizando controladores PID (Normey-Rico et al., 2001) e trajetórias compatíveis com a restrição não-holonômica (Hu et al., 1997) têm sido propostos. Pode-se destacar casos como: Jiang and Nijmeijer (1997) que desenvolveram uma metodologia através da realimentação variante no tempo associada a técnica do integrador de um passo atrás (backstepping) para robôs móveis com acionamento diferencial. Esta técnica foi estendida para sistemas na forma encadeada Jiang and Nijmeijer (1999) e com incertezas (Jiang, 2000) de forma robusta. O controle de trajetória de um navio subatuado empregando o método direto de Lyapunov é tratado em Jiang (2002). O guiamento de veículos marinhos utilizando modelos na forma polar apresentado em e Aicardi, Casalino, Indiveri, Aguiar, Encarnação and Pascoal (2001) e Aicardi, Casalino and Indiveri (2001). Redes neurais são empregadas em sistemas não-holonômicos tanto para localização (Janet et al., 1997), como para controle (Baluja, 1996). Estratégias para rastreamento de trajetórias por modos deslizantes para o robô móvel com acionamento diferencial são propostas por Yang and Kim (1999a), Yang and Kim (1999b) e Chwa et al. (2002).

• Estabilização num ponto: Diversas técnicas têm sido desenvolvidas para a estabilização num ponto de equilíbrio de sistemas não-holonômicos. Sistemas de controle variante no tempo têm sido estudados em profundidade (Morin and Samson, 1996; Morin and Samson, 1995; Morin et al., 1994; Morin et al., 1995; Morin et al., 1999; Morin et al., 1994; Samson and Ait-Abderrahim, 1990; Samson, 1992; Samson and Ait-Abderrahim, 1991; Samson, 1990; Morin and Samson, 1997; Morin and Samson, 1998; Samson, 1995; Morin and Samson, 2000a; Fujimoto and Sugie, 2001; Tian and Li, 2002; Figueiredo and Jota, 2002). A estabilização exponencial, em geral, é obtida empregando-se métodos baseados em funções de Lyapunov. Sordalen and Egeland (1995) apresentam um controlador variante no tempo empregando conceitos de estabilidade exponencial K, que apesar de ser uma forma de estabilidade mais fraca que a estabilidade exponencial, possui a mesma taxa de convergência. A abordagem da estabilização exponencial usando realimentação homogênea variante no tempo é realizada em M'Closkey and Murray (1997). Uma técnica para construir controladores exponencialmente convergentes para sistemas não-holonômicos na forma de potência é apresentada por Luo and Tsiotras (1997); baseia-se num algoritmo recursivo que utiliza uma série de variedades invariantes para construir uma seqüência de sistemas na forma de potência de dimensão reduzida. Utilizando mudanças de coordenadas e uma lei de controle por realimentação de estados descontínua, limitada, e invariante no tempo, Astolfi (1999) propõe um sistema de controle para estabilizar exponencialmente um robô móvel de acionamento diferencial. Utilizando técnicas de Lyapunov, Pourboghrat (2002) estabiliza exponencialmente um robô móvel de acionamento diferencial. Uma transformação descontínua é utilizada para facilitar o projeto do controlador. A estabilização de sistemas não-holonômicos usando fluxos isoespectrais é tratada por Bloch et al. (2000). O sistema na forma de integrador de Brockett é estabilizado usando controle híbrido com chaveamento discreto entre fluxos isoespectrais e norma decrescente. A estabilização de sistemas na forma encadeada através da linearização por realimentação é mostrada em Sun et al. (2001) e Ge et al. (2001). Tayebi et al. (2001) mostram que sistemas n-dimensionais na forma encadeada podem ser estabilizados usando o método da variedade invariante. Primeiro deriva-se uma variedade invariante para esta classe de sistemas e mostra-se, a seguir, que todas as trajetórias em malha fechada tendem para a origem sob uma realimentação de estados suave, linear, invariante no tempo. Mostra-se, ainda, que esta variedade pode se tornar atrativa através de uma realimentação de estados descontínua, invariante no tempo. O controle de sistemas não-holonômicos de ordem alta na forma de potência encadeada usando realimentação descontínua é estudado por Lin et al. (2002). Esta é uma classe particular de sistemas não-lineares que é uma extensão da forma encadeada. A lei de controle é obtida de forma recursiva, através da adição de integradores. A estabilização de sistemas descontínuos empregando a técnica do integrador de um passo atrás (backstepping) é proposta por Tanner and Kyriakopoulos (2002) para robôs móveis com acionamento diferencial. A estabilização de veículos marinhos subatuados é tratada por Indiveri et al.(2000) e Aicardi, Cannata, Casalino and Indiveri (2000a). Pilotos automáticos empregando esta técnica são globalmente estáveis, enquanto que, pela técnica tradicional baseada em modelos linearizados, a estabilidade é local. apresentam resultados para veículos submarinos com incerteza paramétrica usando funções de Lyapunov. A estabilização de sistemas empregando coordenadas polares é abordada por para o robô móvel com acionamento diferencial e em Aicardi, Cannata, Casalino and Indiveri (2000b) para um veículo aquático. Em ambos os casos é mostrado que a mudança de coordenadas gera um sistema holonômico de fácil controle. A técnica de controle por realimentação descontínua pode ser estendida para manipuladores planos subatuados produzindo sistemas estáveis (Mahindrakar et al., 2001). Resultados experimentais de controladores são apresentados tendo como plataforma o robô móvel com acionamento diferencial Khepera (Kim and Tsiotras, 2002). Neste caso, observaram-se características e desempenho de diversos controladores frente a dinâmicas desprezadas, quantização, ruído, atrasos, etc.

• Controle híbrido: Uma revisão da literatura, indicando as bases para sistemas híbridos e seus benefícios no projeto de controladores para sistemas lineares e não-lineares, bem como das diversas metodologias de análise e projeto, podem ser obtidas em Antsaklis et al. (1999), Hespanha (2001a), McClamroch and Kolmanovsky (2000) e Hespanha (2001b). A questão da estabilidade, projeto de sistemas híbridos e ferramentas básicas de análise são apresentadas em Liberzon and Morse (1999), McClamroch et al. (1997), Agrachev and Liberzon (2001), Ye et al. (1998), e Decarlo et al. (2000). Estruturas dinâmicas de transição de controle, aplicação de múltiplas funções de Lyapunov em sistemas chaveados e híbridos, e a utilização de novos conceitos de estabilidade aplicados a sistemas híbridos são apresentados em Sun and Hoo (1999), Branicky (1998), Hespanha et al. (2001). A aplicação da teoria de controle híbrido a sistemas não-holonômicos com exemplos práticos do projeto de controladores é apresentada em Hocherman-Frommer et al. (1998), Hespanha et al. (2002), Hespanha et al. (2001), Lygeros et al. (1996), Piccoli et al. (1998), e Bloch et al. (2000).

• Controle adaptativo: O projeto de controladores adaptativos para rastreamento de sistemas não-holonômicos usando o método do integrador de um passo atrás (backstepping) é proposto por alguns pesquisadores (Fucao et al., 2000; Tayebi and Rachid, 2000; Pourboghrat and Karlsson, 2002; Do and Pan, 2002; Ge et al., 2003). O controle adaptativo para o rastreamento na presença de incertezas quanto ao modelo e estados do sistema usando soluções de controle robusto são considerados por Colbaugh (Colbaugh et al., 1998) e Dong (Dong et al., 2000). Funções de Lyapunov (Aguiar et al., 2000; Sanyal et al., 2003), passividade (Dong and Xu, 2001), modelo preditivo Lizarralde et al., 1999; Fontes, 2002), e estratégias de inteligência artificial (Chang and Chen, 2000; Syam et al., 2001; Syam et al., 2002) são outras ferramentas geralmente utilizadas (veja também (Chang and Chen, 1996; Glass and Colbaugh, 1997; Lefeber and Nijmeijer, 1999; Y-Kuc et al., 2000)). O controle preditivo generalizado (GPC) foi usado no projeto de um sistema de auxílio na condução de um automóvel (DAS) (Horiuchi and Sunada, 1998) o qual ajuda o motorista na tarefa de controle para seguir uma faixa na pista de direção. Este sistema tem a estrutura de um motorista virtual, atuando em paralelo, projetado para agir do mesmo modo que um motorista ideal. Os resultados relatados mostram que a execução da tarefa foi melhorada pelo sistema de controle DAS.

Desse levantamento cronológico/temático sobre trabalhos desenvolvidos na área relativos a controle de sistemas não-holonômicos, depreende-se que esta é uma área sujeita a constantes e rápidas mudanças e que tem recebido contribuições das mais diversas correntes de pensamento. Neste artigo, pretende-se fornecer dados atualizados e mostrar sinteticamente os avanços na teoria e aplicações apresentadas na literatura.

O trabalho está assim dividido: nas seções 2 e 3 são apresentados conceitos básicos de geometria diferencial aplicada a sistemas holonômicos e não-holonômicos, propiciando o reconhecimento de sistemas não-holonômicos e a verificação de sua controlabilidade. Na seção 4 apresenta-se uma aplicação prática destes conceitos. Exemplos de formas canônicas que facilitam o projeto de controladores são apresentados na seção 5. Técnicas de controle em malha aberta e malha fechada e algumas aplicações utilizando como exemplo o robô móvel com acionamento diferencial estão na seção 6. Uma breve discussão das técnicas apresentadas e perspectivas para a área são apresentadas na seção 7.

2 FUNDAMENTOS SOBRE RESTRIÇÕES NÃO-HOLONÔMICAS

O movimento de uma partícula no espaço euclidiano é descrito pelas coordenadas da partícula em cada instante de tempo (Murray et al., 1994), relativas a um sistema de eixos ortogonais x, y, z Î R³. A trajetória da partícula é dada na forma parametrizada por p(t) = (x(t),y(t),z(t)) Î R³. Muitas vezes não estamos interessados no movimento de uma partícula, mas no de um corpo (articulado ou não) composto por diversas partículas. Para simplificar o estudo podemos assumir que o corpo é indeformável (corpo rígido), neste caso, a distância entre duas partículas quaisquer deste corpo será fixa. Logo, se p e q são as posições de duas partículas deste corpo, então a relação abaixo deve ser satisfeita:

||p(t) – q(t)|| = ||p(0) – q(0)|| = constante.

Um movimento rígido de um objeto é um movimento contínuo de partículas no objeto de forma tal que a distância entre duas partículas quaisquer seja preservada. Este movimento é representado por uma família de mapeamentos g(t): O ® R³ (onde O é o conjunto de vetores-eixos ortogonais). Nota-se que a condição de preservação de distância é uma condição necessária, mas não suficiente, para que g(t) seja o mapeamento deste movimento, pois a orientação não é preservada. Para atender a este último requisito, o produto vetorial entre vetores pertencentes ao corpo também deve ser preservado. Assim para rastrear o movimento de qualquer partícula num corpo rígido basta rastrear o movimento de uma partícula sobre o corpo e a rotação do mesmo em torno deste ponto.

Esta relação entre partículas (limitação do grau de liberdade) é chamada de restrição. Cada restrição pode ser representada por uma função g_j : R³ⁿ ® R tal que

g_j(r₁,..., r_n) = 0, j = 1,...k

ou seja, como uma relação algébrica entre as posições das partículas. Tal restrição define uma hiper-superfície (Dubrovin et al., 1984) ou variedade, logo, o movimento será limitado a esta hiper-superfície. Tal restrição é chamada de holonômica, ou integrável. Uma restrição age sobre um sistema de partículas através da aplicação de forças de restrição. Se considerarmos as restrições como hiper-superfícies suaves em Rⁿ, as forças de restrição são normais a esta hiper-superfície e restringem a velocidade do sistema a ser tangente a esta superfície em qualquer instante de tempo. Uma vez que restrições holonômicas definem uma hiper-superfície suave no espaço de configuração, é possível eliminar estas restrições pela escolha de novas coordenadas apropriadas a esta superfície (Murray et al., 1994). Estas novas coordenadas parametrizam todos os movimentos permitidos do sistema e não estão sujeitas a qualquer outra restrição.

Uma restrição de um tipo fundamentalmente diferente ocorre sempre que os movimentos permissíveis do sistema estão limitados por restrições de velocidade da forma

A(q) = 0,

onde A(q) Î R^k×n representa um conjunto de k restrições de velocidade. Uma restrição desta forma é chamada de restrição Pfaffiana. Uma vez que uma restrição Pfaffiana limita as velocidades permissíveis do sistema mas não necessariamente as configurações, não se pode, em geral, representa-la como uma restrição algébrica sobre o espaço de configuração. Uma restrição Pfaffiana é dita ser integrável se existir uma função vetorial h: Q ® R^k tal que

Assim, uma restrição Pfaffiana integrável é equivalente a uma restrição holonômica.

Uma restrição Pfaffiana que não é integrável é um exemplo de restrição não-holonômica. Restrições não-holonômicas deste tipo ocorrem quando as velocidades instantâneas do sistema são limitadas a um subespaço de dimensão n – k, porém o conjunto de configurações atingíveis não está restrito a uma superfície n – k dimensional no espaço de configuração.

Deseja-se descobrir como a condição não-holonômica das restrições pode ser explorada para se obter deslocamentos entre configurações diferentes, ou seja, verificar se é possível deslocar por um caminho q(t) do ponto q₀ ao ponto q_f satisfazendo às restrições não-holonômicas.

A determinação se um sistema é ou não holonômico não é uma tarefa fácil. Seja o caso no qual existe uma única restrição de velocidade (Murray et al., 1994):

Esta restrição é integrável se existe uma função h : Rⁿ ® R tal que

w(q)= 0 Û h(q) = 0.

Se a restrição Pfaffiana é holonômica, diferenciando h(q) = 0 com relação ao tempo, segue então que:

Por sua vez, isto implica que existe alguma função a(q), chamada de fator de integração, tal que:

Logo, uma restrição Pfaffiana é holonômica se e somente se existir um fator de integração a(q) tal que a(q)w(q) seja a derivada de alguma função h. Para facilitar a verificação pode-se usar o fato de que

para obter

que é equivalente à afirmação de que h(q) = 0 se existir algum fator de integração a(q) que satisfaça à equação acima. A situação se complica ainda mais para o caso de múltiplas restrições Pfaffianas. Para um conjunto de k equações de restrição, deve-se não apenas verificar a integrabilidade de cada uma mas também a de combinações linearmente independentes destas. Assim, podem existir funções h_i para i = 1,...,p com p < k tal que

para todo q, onde o operador var {.} indica a varredura ou base criada pelos vetores especificados. Se for possível achar estas funções, o movimento do sistema estará restrito a superfícies de nível de h. Se p = k, então as restrições são holonômicas. Quando p < k, as restrições não são holonômicas porém os pontos atingíveis do sistema continuam restritos. Logo, as restrições são parcialmente holonômicas. Para fins de controle, esta-se interessado em situações nas quais as restrições não limitam as configurações atingíveis. Estes casos são chamados de completamente não-holonômicos.

3 FERRAMENTAS BÁSICAS PARA O ESTUDOS DE SISTEMAS NÃO-HOLONÔMICOS

Em vários casos, é necessário converter problemas com restrições não-holonômicas para uma outra forma, ou seja, ver o problema não do ponto de vista das direções onde o movimento não é possível e sim o contrário. Isto pode ser conseguido escolhendo-se uma base para o espaço nulo à direita das restrições, denotado por g_j(q) Î >Rⁿ, j = 1,...,n – k =: m. Por construção esta base satisfaz

e as trajetórias permissíveis para o sistema podem ser escritas como as possíveis soluções do sistema de controle

Isto é, q(t) é uma trajetória realizável para o sistema se e somente se q(t) satisfaz à equação (1) para algum valor dos controles u(t) Î R^m. Neste contexto, uma restrição é completamente não-holonômica se os estados do sistema correspondente podem ser deslocados de um estado inicial a outro final qualquer. Logo, o espaço de atingibilidade das configurações do sistema não está restrito. Por outro lado, se a restrição é holonômica, então todos os movimentos do sistema estão confinados numa superfície limitada e os estados do sistema correspondente só podem se mover sobre esta variedade. Assim, pode-se estudar a natureza das restrições Pfaffianas estudando as propriedades de controlabilidade da equação (1).

Para facilitar o entendimento desta abordagem serão considerados sistemas de controle sem deriva (em que os estados dependem apenas das entradas correspondentes) em Rⁿ. Seja T_qRⁿ o espaço tangente a Rⁿ no ponto q Î Rⁿ. Um campo vetorial sobre Rⁿ é um mapa suave que atribui a cada ponto q Î Rⁿ um vetor tangente f(q) Î T_qRⁿ, tal que

Um campo vetorial será suave se cada vetor f_i(q) for suave. Campos vetoriais podem ser imaginados como o lado direito de equações diferenciais:

Associado a um campo vetorial, define-se o fluxo de um campo vetorial como a representação da solução da equação diferencial (2). Especificamente (q) representa o estado da equação diferencial no instante t partindo de q no instante 0. Assim (q):Rⁿ® Rⁿ satisfaz

A taxa de variação de uma função suave V :Rⁿ ® R ao longo do fluxo de f é dada por

A derivada no tempo de V ao longo do fluxo de f é referenciada como a derivada de Lie de V ao longo de f e denotada por L_fV:

Um mapeamento T : D ® Rⁿ é um difeomorfismo (Khalil, 1996) sobre D se ele for invertível sobre D, isto é, existe uma função T^–1(x) tal que T^–1(T(x)) = x para todo x Î D, e tanto T(x) quanto T^–1(x) são continuamente diferenciáveis. Se a Matriz Jacobiana for não-singular num ponto x₀Î D, então segue do teorema da função inversa que existe uma vizinhança N de x₀ tal que T restrito a N é um difeomorfismo sobre N.

Um campo vetorial é dito ser completo se seu fluxo está definido para todo t. Pelo teorema da existência e unicidade das equações diferenciais ordinárias, para cada t fixo, é um difeomorfismo local de Rⁿ sobre ele próprio. Além disto, ele satisfaz à propriedade de grupo:

para todo t e s, onde "º" indica a composição de dois fluxos (((q))).

Define-se a operação denominada colchete de Lie (Dubrovin et al., 1984) como:

que satisfaz às seguintes propriedades:

1. Bilinearidade

2. Anticomutatividade

[A, B] = – [B, A]

3. Identidade de Jacobi

[A, [B, C]] + [C, [A, B]] + [B,[C, A]] = 0

O colchete de Lie para dois campos vetoriais f e g é definido como

e pode ser interpretado como o movimento infinitesimal resultante do fluxo em torno de um quadrado definido por dois campos vetoriais f e g. Se este movimento for nulo, diz-se que os campos comutam. Isto pode ser melhor visualizado para operadores lineares (matrizes), onde o colchete de Lie é definido como produto vetorial

[A, B] = A B – B A;

se A e B comutarem, o colchete de Lie será nulo. O colchete de Lie algumas vezes é chamado de comutador.

Uma distribuição atribui um subespaço do espaço tangente a cada ponto em Rⁿ de um modo suave. Seja g₁,g₂, ...,g_k campos vetoriais sobre V Ì Rⁿ. Em qualquer ponto fixo q Î V, g₁(q),g₂(q), ..., g_k(q) são vetores em Rⁿ e

D(q) = var{g₁(q),g₂(q), ..., g_k(q)} Ì T_qRⁿ

é um subespaço de Rⁿ. Para cada ponto q Î Rⁿ, atribui-se um subespaço D(q), referenciado como

D = var{g₁,g₂, ...,g_k}.

Em outras palavras, uma distribuição D é uma coleção de todos os espaços vetoriais D(q) para q Î V.

Uma distribuição é dita ser regular se a dimensão do subespaço D(q) não varia com q. Uma distribuição é involutiva se ela for fechada sob o colchete de Lie, isto é,

D involutiva Û "f, g Î D, [f,g] Î D.

Para uma distribuição de dimensões finitas é suficiente verificar se os colchetes de Lie dos elementos-base estão contidos na distribuição. O fechamento involutivo de uma distribuição, denotado por , é o fechamento de D sob a operação colchete de Lie; ou seja, é a menor distribuição contendo D tal que se f,g Î então [f, g] Î .

Um espaço vetorial real V onde a operação colchete de Lie está definida é denominado de álgebra de Lie e aqui denotado por (Rⁿ). Seja g₁,...,g_m um conjunto de campos vetoriais suaves, D a distribuição definida por estes campos vetoriais, e o fechamento involutivo de D, logo é uma álgebra de Lie e é denotado por (g₁,...,g_m). Os elementos de (g₁,...,g_m) são obtidos tomando-se todas as combinações lineares dos elementos de g₁,...,g_m, tomando-se os colchetes de Lie destes, tomando-se todas as combinações lineares destes, e assim por diante. Define-se o posto de (g₁,...,g_m) num ponto q Î Rⁿ como sendo a dimensão de _q como uma distribuição.

Uma distribuição D de dimensão k constante é dita ser integrável se, para todo ponto q Î Rⁿ, existe um conjunto de funções suaves h_i : Rⁿ ® R, i = 1,..., n – k tal que os vetores linha são linearmente independentes em q, e para todo f Î D

As hiper-superfícies definidas pelos conjuntos níveis

{q : h₁ = c₁,..., h_n–k(q) = c_n–k}

são chamadas variedades integrais da distribuição. Imagina-se uma variedade integral como uma superfície suave em Rⁿ, então a equação (3) requer que a distribuição seja igual ao espaço tangente desta superfície no ponto q.

Variedades integrais estão relacionadas com distribuições involutivas pelo célebre teorema de Frobenius (Arnol'd and (Eds.), 1994) que afirma que uma distribuição regular é integrável se e somente se ela for involutiva. Assim, se D é uma distribuição involutiva k-dimensional, então localmente existem n – k funções h_i : Rⁿ ® R tal que variedades integrais de D são dadas pelas superfícies de nível de h = (h₁,...,h_n–k).

Associado com o espaço tangente T_qRⁿ está o espaço dual Rⁿ, o conjunto de funções lineares sobre T_qRⁿ. Tal como foram definidos campos vetoriais sobre Rⁿ, define-se uma uma-forma como um mapa que atribui a cada ponto q Î Rⁿ um covetor w(q) Î Rⁿ. Em coordenadas locais representa-se uma uma-forma suave como um vetor linha

w(q) = [w₁(q) w₂(q) ... w_n(q)].

Diferenciais de funções suaves são bons exemplos de uma-forma. Por exemplo, se b : Rⁿ ® R, então a uma-forma db é dada por

Uma uma-forma age sobre um campo vetorial para gerar uma função real sobre Rⁿ tomando o produto interno entre um vetor linha w e um vetor coluna f:

Uma codistribuição atribui um subespaço de R suavemente a cada q Î Rⁿ. Um caso especial é uma codistribuição obtida como uma varredura de um conjunto de umas-forma,

W = var{w₁, ..., w_n},

onde a varredura está sobre o conjunto de funções suaves. O posto da codistribuição é a dimensão de W_q. A codistribuição W é dita ser regular se seu posto for constante.

No planejamento de movimento para sistemas não-holonômicos, a primeira tarefa é converter as restrições dadas como umas-forma num sistema de controle equivalente. Para isto, considere o problema de construir um caminho q(t) Î Rⁿ entre um dado q₀ e q_f sujeito às restrições

w_i(q) = 0 i = 1, ..., k.

Os w_i's são funções lineares sobre os espaços tangentes de Rⁿ, isto é, umas-forma. Considerando que os w_i's são suaves e linearmente independentes sobre o conjunto de funções suaves, a seguinte proposição (Murray et al., 1994) é uma formalização da discussão da Introdução.

Proposição 1. Distribuição aniquilando restrições

Dado um conjunto de umas-forma w_i(q), i = 1,..., k, existem campos vetoriais suaves, linearmente independentes g_j(q), j = 1,..., n – k tal que w_i(q) · g_j(q) = 0 para todo i e j.

Na linguagem de distribuições e codistribuições, os resultados desta proposição são expressos definindo a codistribuição

W = var{w₁, ..., w_k}

e a distribuição

D = var{g₁, ..., g_{n – k}}

e declarando que

D = W^{^}.

Diz-se que a distribuição D aniquila a codistribuição W. O sistema de controle associado com a distribuição D é da forma

= g₁(q)u₁ + ... + g_{n – k}(q)u_{n – k},

com os controles u_i a serem livremente especificados. Estes resultados podem ser usados para determinar se um conjunto de restrições são holonômicas através da proposição seguinte:

Proposição 2. Integrabilidade de restrições Pfaffianas

Um conjunto de restrições Pfaffianas suaves é integrável se e somente se a distribuição que aniquila as restrições é involutiva.

Considerando a proposição 1, que produz um conjunto de campos vetoriais ortogonais a um dado conjunto de umas-forma, fica claro que o problema do planejamento de movimento é equivalente ao do deslocamento dos estados de um sistema de controle. Assim, restringe-se a atenção a sistemas de controle da forma

Este sistema é dito livre de deriva, o que significa dizer que quando os controles são colocados em zero os estados do sistema não se alteram. Considerando g_j campos vetoriais suaves, linearmente independentes sobre Rⁿ e que seus fluxos são definidos durante todo o tempo, deseja-se determinar as condições sob as quais pode-se deslocar o sistema de q₀Î Rⁿ para um q_f Î Rⁿ arbitrário, pela escolha de um sinal u(.) adequado.

Um sistema S é controlável se para qualquer q₀, q_f Î Rⁿ existe um T > 0 e u : [0, T] ® U tal que S satifaz q(0) = q₀ e q(T) = q_f. Um sistema é dito ser localmente controlável a curto tempo em q₀ se pontos próximos podem ser atingidos num intervalo de tempo arbitrariamente curto e permanecer sempre próximo de q₀. Dado um conjunto aberto V Í Rⁿ, define-se ^V(q₀, T) como sendo o conjunto de estados q tal que exista u : [0, T] ® U que desloca S de q(0) = q₀ até q(T) = q_f e satisfaz q(t) Î V para 0 < t < T. Também define-se

como sendo os estados atingíveis até o tempo T. Um sistema é localmente controlável a curto tempo se ^V (q₀, t < T) contém uma vizinhança de q₀ para todas as vizinhanças de V de q₀ e T > 0.

O Teorema de Chow (Murray et al., 1994) afirma que um sistema de controle (4) é localmente controlável em q Î Rⁿ se _q = T_qRⁿ. Este resultado comprova que um sistema sem deriva S é controlável se o posto da matriz de controlabilidade da álgebra de Lie for n. A condição do teorema de Chow consiste em verificar o posto da álgebra de Lie de controlabilidade e será aqui referenciado como condição de posto de controlabilidade.

Em princípio, tem-se agora uma receita para resolver o problema do planejamento de movimento para sistemas que satisfaçam a condição de posto de controlabilidade. Dado um ponto inicial q₀ e um ponto final q_f, encontra-se um número finito de caminhos intermediários q₁, q₂,..., q_p Î Rⁿ e vizinhanças de V_i tal que

contenha segmentos de linha reta conectando q₀ a q_f. Então existe uma lei de controle com p segmentos que desloca o sistema de q₀ até q_f. A dificuldade deste procedimento (e dos teoremas aqui apresentados) é que eles não mostram como construir o caminho juntando q₀ a q_f, só provam sua existência.

4 APLICAÇÃO A UM ROBÔ MÓVEL COM ACIONAMENTO DIFERENCIAL

Um robô que se move com acionamento diferencial é o exemplo utilizado como base de comparação no desenvolvimento de estratégias de controle para sistemas não-holonômicos. Para reduzir o espaço de configuração, considera-se que o robô possui três rodas, duas acionadas individualmente e uma terceira que gira livremente, cuja função é apenas servir de suporte para o robô (evitar que ele se incline quando se move sobre um plano). Considera-se que esta terceira roda tem efeitos desprezíveis na dinâmica do veículo. As duas rodas acionadas individualmente são responsáveis pelo movimento do robô e diferenças de velocidade entre as mesmas fazem com que o robô mude sua orientação. No caso limite, uma roda girando em sentido contrário ao da outra com o mesmo módulo de velocidade provocam a rotação do robô em torno do seu eixo. O corpo do robô tem uma forma simétrica e o centro de massa está no centro geométrico do corpo.

Tal sistema está representado na Figura 1, onde a posição do mesmo está representada tanto em coordenadas retangulares quanto polares. A posição do centro geométrico em coordenadas retangulares é dada por (xo, yo) e f é o ângulo entre o eixo central do robô (sentido longitudinal) e o eixo x do sistema de coordenadas, representando a direção à frente. O sistema também pode ser representado em coordenadas polares (r, q). A velocidade linear do robô é dada por v_o, e w_o indica a velocidade angular.

A postura do robô, q, é definida (Yang and Kim, 1999b) como

q = [x_o, y_o, f]^T.

O robô móvel tem restrição não-holonômica já que as rodas acionadas apenas giram para frente ou para trás e não deslizam lateralmente, podendo esta ser escrita como

_o cos(f) 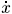– _o sen(f) = 0.

Portanto o sistema tem espaço de configuração tri-dimensional (n = 3) e uma restrição (p = 1) o que leva a um vetor de velocidade de dimensão m = n – p = 2. Escolhendo v_o e w_o como as variáveis de estado internas tais que

z = [v_o, w_o]^T,

obtém-se a equação na forma (4) como:

Logo, tem-se que (Victorino, 1998)

O posto da matriz formada por (g₁, g₂) é dois e inferior ao espaço de configuração, portanto, deve-se gerar o colchete de Lie [g₁, g₂] para verificar se o sistema é holonômico e a possibilidade de completar a distribuição para verificar se o sistema é controlável. Logo

e do teorema de Frobenius, se o sistema = G.u é completamente integrável (holonômico) então ele é involutivo, ou seja

Posto(g₁g₂) = Posto(g₁g₂ [g₁, g₂])].

A verificação leva a:

Com isto conclui-se que o sistema é não-holonômico. Pelo teorema de Chow (condição de posto da álgebra de Lie) tem-se que o posto do sistema acrescido de g₃ é igual ao do espaço de configuração, logo o sistema é controlável.

5 FORMAS CANÔNICAS

Está-se principalmente interessado na construção de sistemas não-holonômicos que sejam canônicos (Murray and Sastry, 1993) no sentido de que permitam a expansão máxima por colchete de Lie dos campos vetoriais G = (g₁, g₂, ..., g_m). Bases que sejam álgebras de Lie possuem esta propriedade inerente. A base de Philip Hall (Kreyszig, 1991) é uma álgebra de Lie e permite tal expansão além de levar em consideração as propriedades anti-simétrica e a identidade de Jacobi durante a expansão (Murray et al., 1994). Classes bem conhecidas de sistemas não-holonômicos são aquelas na forma encadeada (Kolmanovsky and McClamroch, 1995) dadas por sistemas do tipo

e de sistemas na forma de potência, dadas por

Ambas as classes acima satisfazem a condição de não-holonomicidade completa do teorema de Chow, portanto, são controláveis. As duas formas são equivalentes através de uma transformação de estados.

A forma de integrador não-holonômico ou sistema de Heisenberg ou integrador de Brockett é dada por:

onde x₁, u₁, x₂, u₂, x₃Î R. Este sistema pode ser representado na forma compacta empregando a definição de colchete de Lie como (Bloch et al., 2000):

onde u = (u₁, u₂), x = (x₁, x₂) e Y = .

Sistemas na forma cartesiana como o do robô móvel com acionamento diferencial podem ser convertidos para a forma do integrador não-holonômico (6) através da aplicação da seguinte transformação de coordenadas (Hespanha et al., 1999a):

Ao invés de representar o robô móvel com acionamento diferencial na forma cartesiana, sugerem a representação do mesmo em termos de coordenadas polares, envolvendo o erro de distância e > 0 e sua orientação f em relação à origem da base < g > , desta forma obtêm-se:

Fazendo a = f – q como sendo o ângulo medido entre o eixo principal do veículo e o vetor distância e, chega-se a:

Utilizando esta última forma, o projeto de leis de controle lineares, invariantes no tempo, em malha fechada se torna direto. Entretanto, deve ser observado que as equações somente são válidas quando o erro do vetor distância é diferente de zero ou que simultaneamente sen(a) também seja zero.

6 CONTROLE DE SISTEMAS NÃO-HOLONÔMICOS

O controle de sistemas não-holonômicos pode ser agrupado como na teoria clássica de controle em: métodos de malha aberta e métodos de malha fechada. Os métodos de malha aberta são também conhecidos como planejamento do movimento para sistemas não-holonômicos e buscam leis de controle em malha aberta que desloque o sistema de um estado inicial até um estado final. Já os métodos de malha fechada são aqueles que possuem alguma lei de realimentação para estabilizar o sistema em torno de um ponto de equilíbrio, seguir uma trajetória, ou rejeitar distúrbios.

6.1 Métodos de malha aberta

Tais métodos, em contraste com técnicas tradicionais, devem levar em consideração as restrições instantâneas ao movimento. As técnicas mais difundidas são as baseadas em:

• Geometria diferencial e álgebra diferencial

• Fase geométrica

• Parametrização da entrada

• Controle ótimo do movimento

• Planejamento do movimento evitando-se obstáculos

Métodos empregando geometria diferencial e álgebra diferencial

Utilizam extensivamente o conceito de colchete e álgebra de Lie para o planejamento do movimento, encontra-se entre seus maiores defensores pesquisadores como G. Lafferriere e Héctor J. Sussmann. O primeiro método neste grupo utiliza entradas constantes por parte para gerar movimentos nas direções dos colchetes de Lie e é chamado de método de aproximação nilpotente (Lafferriere and Sussmann, 1991). Baseia-se no fato de que, se um sistema de controle pode ser expandido pelo colchete de Lie (é uma álgebra de Lie), então têm-se duas situações: se o sistema é nilpotente existe uma solução única para o problema, caso contrário, pode-se aplicar um método de nilpotencialização por realimentação através de um pré-compensador e fazer com que um algoritmo de controle produza uma solução exata num número finito de passos.

O método de aproximação nilpotente considera que o sistema é completamente controlável, não possui deriva e é formado por campos vetoriais reais e analíticos. A primeira condição é equivalente à condição do posto da álgebra de Lie (LARC) ou condição de posto de controlabilidade. Uma álgebra de Lie é dita ser nilpotente se existe um inteiro k > 0 com a propriedade de que todos os colchetes de Lie [v₁, [v₂, ..., [v_k, v_k+1] se anulam. O menor deste k é a ordem de nilpotência da álgebra de Lie, e a álgebra de Lie é dita ser nilpotente de ordem k. Para ilustrar, o sistema será de ordem um se [f_i, f_j] = 0 para todo i, j, ou seja, se o sistema for abeliano (comutativo). Lafferriere and Sussmann (1991) mostraram que, se a ordem de nilpotência for igual ou maior que o número de estados do sistema, pode-se então criar um sistema estendido, achar um controle v que desloca p para q para o sistema estendido e então achar u que desloca p para q no sistema original. Para facilitar a expansão do sistema (evitar termos anti-simétricos e que satisfazem a identidade de Jacobi) é utilizada a base de Philipp Hall.

Muitos sistemas que não são nilpotentes podem ser transformados em sistemas nilpotentes através de realimentação que consiste numa mudança linear dos controles

tal que b(x) seja uma matriz não singular para cada x, e b(x) seja suave como função de x.

Considerando o robô descrito anteriormente, em que os controles são a velocidade de acionamento e a velocidade angular, as equações para o sistema são:

onde (x₁, x₂) são as coordenadas cartesianas do centro do robô e x₃ é o ângulo que seu eixo principal faz com o eixo x₁. Pode-se reescrever o sistema como 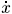= u₁f₁(x) + u₂f₂ (x) onde

f₁(x) = (cos(x₃), sen(x₃), 0) f₂(x) = (0,0,1).

Vê-se que os vetores f₁(x),f₂(x), [f₁, f₂](x) varrem R³ próximo de x = 0, de forma que o sistema é nilpotencializável porém o mesmo não é nilpotente. O sistema pode ser tornado nilpotente usando a seguinte realimentação

O sistema é transformado então em

o qual é nilpotente de ordem 2. Calculam-se então os sinais de controle desejados como segue. Primeiro aplica-se o procedimento ao sistema nilpotente para obter os controles w_i; então usando a realimentação calcula-se os controles para o sistema original. A solução para o sistema estendido será da forma

O movimento no sentido de [f₁, f₂] é equivalente ao deslocamento do sistema na direção de f₁ por Dt segundos, seguida na direção f₂ por Dt segundos, na direção – f₁ por Dt segundos, e finalmente na direção –f₂ por Dt segundos.

Sussmann and Liu (1997) propuseram um método que emprega entradas altamente oscilatórias. A idéia deste método é tomar um caminho g : [0, T] ® M tal que g(0) = p, g(T) = q, que não precisa ser admissível, e tentar-se aproximar deste caminho total através de uma seqüência {g_i} de caminhos admissíveis, também definidos sobre [0, T], e também satisfazendo às condições iniciais. Para tal, estende-se o sistema original empregando o colchete de Lie e então expressa-se o caminho g como uma trajetória no novo sistema correspondente a alguma entrada estendida v. Tenta-se encontrar uma seqüência de entradas comuns u^j cujas trajetórias convergem para as entradas estendidas. Usam-se entradas de controle periódicas de alta freqüência e alta amplitude para gerar movimento na direção dos novos campos vetoriais (gerados pelos colchetes de Lie). O resultado do movimento médio do sistema, obtido no limite destas entradas de alta freqüência, é um deslocamento preciso (dentro de uma determinada tolerância). Os sinais de controle são do tipo = h₁(t) + h₃(t) senjt. Deve-se tomar cuidado para escolher freqüências e coeficientes de forma que os sinais de controle resultantes sejam reais. Este método tem uso limitado devido ao tipo de sinal de controle utilizado. Pode ser utilizado como aproximação inicial para problemas em que seja necessário evitar obstáculos.

Método usando fase geométrica

Este método se aplica a sistemas de controle não-holonômicos do tipo cinemático de Chaplygin. Consiste na determinação da alteração resultante no vetor fibra baseado na integral de linha ao longo do caminho do vetor base quando este é submetido a um movimento cíclico. O valor desta integral de linha independe de qualquer parametrização do caminho, dependendo apenas da geometria do mesmo; assim, este valor é referenciado como a geometria de fase (Kolmanovsky and McClamroch, 1995). O problema então se reduz à determinação de um caminho base que produza a desejada geometria de fase.

O emprego do teorema de Stokes e a expansão em série de Taylor permitem a expansão da integral de linha utilizando colchetes de Lie. Para um sistema nilpotente esta série termina após um número finito de termos, fornecendo desse modo uma expressão explícita para a geometria de fase.

Este método foi usado para resolver problemas de reorientação de satélites no espaço e para explicar como os movimentos cíclicos dos cílios sobre a superfície do paramecium provoca o movimento do mesmo (Murray et al., 1994).

Métodos de Parametrização da entrada

Brockett mostrou (Murray et al., 1994) que para sistemas de controle descrito por equações como (1), os sinais de controles que levam uma função de energia a ser otimizada da forma:

onde a primeira parte do lado direito representa o quadrado do sinal de entrada e a segunda parte corresponde as restrições ao movimento; são sinais periódicos, mais especificamente, senóides. O sinal ótimo é obtido aplicando-se as equações de Euler-Lagrange para minimizar a função Lagrangeana acima. A solução do sistema indica que é constante e que os sinais que satisfazem o sistema resultante (uma matriz real anti-simétrica, portanto, possuindo autovalores complexos conjugados) são senóides de freqüência .

Baseados nestes resultados, Murray and Sastry (1993) propuseram um método de deslocamento por parametrização da entrada usando senóides. Para sistemas que se tornam completamente não-holonômicos com apenas o primeiro nível de colchete de Lie ([g_i, g_j]) o método consiste basicamente em: deslocar os x_i's até que seus valores finais sejam atingidos usando um sinal qualquer e ignorando a evolução dos estados x_ij's; usando senóides com freqüências múltiplas, encontrar u₀ que desloca os estados x_ij's até o valor objetivado. Esta última ação mantém os estados x_i's inalterados (sinal periódico) enquanto gera um deslocamento nos estados x_ij's. O método pode ser estendido a sistemas de segunda ordem (onde é necessário um segundo nível de colcheteamento para varrer todo o espaço tangencial em q). Neste caso, os dois passos anteriores são aplicados acrescidos de um terceiro: utilizam-se entradas senoidais uma segunda vez para mover todos os estados previamente deslocados e gerar movimento apenas nas direções x_ijk's.

Método de controle ótimo do movimento

Sussmann (1991) considera o controle ótimo um método natural para problemas de busca de caminhos para sistemas não-holonômicos. Em muitos casos, existe uma função que se deseja minimizar ou quase minimizar. E, mesmo que a escolha desta função não seja óbvia, a transformação artificial do problema de encontrar um caminho em um de otimização é desejada.

A principal limitação do método por controle ótimo é que, exceto em alguns casos muito especiais, os sinais de controle ótimo são muito difícieis de se calcular. Entretanto, usando métodos recentes da geometria diferencial, algum progresso pode ser obtido para sistemas que não podem ser tratados pelos métodos clássicos de controle ótimo.

Pode-se aplicar o método de controle ótimo por mínimos quadrados para sistemas na forma da equação (1), quando o mesmo atende a condição de posto de controlabilidade. A função de custo a ser minimizada será do tipo

Murray et al. (1994) apresentam uma derivação heurística das condições necessárias para otimalidade usando cálculo de variações. Neste caso a função de custo deve incorporar as restrições usando uma função multiplicadora de Lagrange p(t), obtendo

Prova-se (Murray et al., 1994) que a norma da entrada ótima é constante, isto é,

||u(t)||² = ||u(0)||²"t Î [0,1].

Desenvolvendo o sistema acima obtém-se

= W(q, p)u

onde W(q, p) é uma matriz anti-simétrica dada por

A solução da equação é da forma

u(t) = U(t)u(0)

para algum U(t) Î SO(m). Brockett e Dai (Kolmanovsky and McClamroch, 1995) demostraram a otimalidade de sinais de controle senoidais e elípticos que satisfazem o sistema acima.

Métodos de planejamento do movimento evitando-se obstáculos

Existe uma distinção entre método de deslocamento e de planejamento do caminho evitando-se obstáculos. Enquanto o primeiro busca funções de entradas para seguir uma trajetória utilizando tanto métodos de malha aberta quanto de malha fechada, o segundo preocupa-se em gerar uma trajetória livre de obstáculos. Pode-se citar como métodos de deslocamentos aqueles que buscam caminhos ótimos, sistemas com entradas senoidais (Sekhavat and Laumond, 1998) e na forma encadeada, métodos de deslocamento baseado na planicidade para robôs móveis com reboques, dentre outros (Laumond, 1998). Para o planejamento de caminhos na presença de obstáculos, destacam os métodos: derivação a partir de caminhos holonômicos, probabilístico, utilizando técnicas de otimização, espaço de caminho, multi-nível, empregando técnicas de inteligência artificial (algoritmo A estrela), etc. Métodos desenvolvidos para sistemas na ausência de obstáculos podem ser estendidos para sistemas com obstáculos dependendo de algumas propriedades topológicas destes (Laumond et al., 1994).

A grande maioria destes métodos inicia a construção do caminho desprezando as restrições não-holonômicas, buscando apenas um caminho realizável. Nesta fase, os métodos descritos anteriormente para deslocamento do sistema e outros mais comuns são empregados. Encontrada uma trajetória realizável, são introduzidas as restrições não-holonômicas e um caminho livre de obstáculos sujeito a restrições não-holonômicas é obtido.

Para sistemas não-holonômicos simples do tipo robô móvel é possível planejar caminhos melhores usando esqueletos (Mirtich and Canny, 1992; Kolmanovsky and Mc-Clamroch, 1995). Um esqueleto é uma coleção de caminhos fixos (geralmente não realizáveis) que estão de forma máxima livres de obstáculos. O sistema é forçado a seguir o esqueleto de um estado inicial até um estado final enquanto evita obstáculos. Uma vez que o esqueleto fica de forma máxima livre de obstáculos, o caminho resultante tende a ser de baixa complexidade.

6.2 Métodos em malha fechada

Muitas vezes é necessária a utilização de controle por realimentação. Dependendo do tipo de resposta desejada existem diversas formulações para o problema de controle. Pode-se destacar três abordagens mais comuns (Khalil, 1996): estabilização, rastreamento, e rejeição / atenuação de distúrbios (e várias combinações das mesmas). No caso da estabilização, procura-se leis de realimentação (variantes ou invariantes no tempo) que estabilizem um sistema para um determinado ponto de equilíbrio. Para o rastreamento, a meta básica é projetar um sinal de controle de forma que a saída controlada y siga um sinal de referência y_R, isto é,

e(t) = y(t) – y_R(t) » 0, "t > t₀

onde t₀ é o instante em que o controle se inicia. Como o valor inicial de y depende do estado inicial (x₀), é necessário partir de um estado "pré-estabelecido".

Um postulado bem conhecido dos pesquisadores em controle não-linear proposto por Brockett (1983) diz que: Um sistema não-holonômico, embora seja completamente controlável, não pode ser estabilizado para uma configuração final de repouso através de leis suaves de realimentação nos estados. Este postulado se aplica à estabilização em torno de um ponto de equilíbrio e leis de controle invariantes no tempo, porém não é válido para o rastreamento de uma trajetória (Victorino, 1998). Neste último caso, pode-se usar as leis de controle conhecidas se o sistema for linearizável por realimentação estática ou dinâmica de estados, e uma vez que a trajetória de referência não contenha configurações de repouso.

Para sistemas lineares invariantes no tempo, se os autovalores instáveis do sistema são controláveis, então a origem pode ser estabilizada de forma assintótica. Sistemas não-holonômicos apresentam características que o diferenciam consideravelmente do caso anterior. Mesmo que linearizado em torno de um ponto de operação, o sistema não é assintoticamente estável, logo, as estratégias tradicionais não podem ser empregadas. As principais técnicas de controle desenvolvidas para vencer esta limitação são:

• Estabilização variante no tempo;

• Estabilização usando sinais não contínuos ou transformações não-lineares;

• Leis híbridas de realimentação.

Restringe-se a abordagem aqui a exemplos da utilização do método de rastreamento de trajetória por linearização dinâmica, estabilização variante no tempo e não contínua em um ponto de equilíbrio e uma lei híbrida.

Rastreamento de trajetórias não-singulares usando realimentação dinâmica de estados

Será considerado aqui o robô móvel com acionamento diferencial, constituído por duas rodas acionadas individualmente e uma terceira de apoio com giro livre, construído de tal forma que o mesmo possa girar em torno do próprio eixo, conforme é mostrado na Figura 1. O seguinte modelo cinemático descreve o comportamento deste robô:

onde j é o vetor de saída (x, y) a posição do robô, q a orientação do mesmo, h₁ sua entrada para a velocidade linear associada e h₂ para a respectiva velocidade angular. Este vetor de entradas de controle h_i está relacionado com as velocidades das rodas por

ou de forma inversa

O método de linearização por realimentação estática pode ser resumido, em poucas linhas, como a seguir (Slotine and Li, 1991).

Considere o seguinte sistema não-linear:

onde i = 1,..., n, f(x) é um vetor de dimensão n de funções suaves, G(x) é uma matriz de dimensão n × m de funções suaves de elementos g_ij. Os vetores x e u de dimensões n e m, respectivamente, são os vetores de estado e de entrada de controle. O projeto de uma lei de controle que linearize o sistema com realimentação estática é então estabelecido seguindo-se os passos:

• escolher uma função de saída de dimensão m, y = h(x) = (y₁(x)...y_m(x)) que corresponda a uma matriz de controlabilidade desacoplada não-singular após a realimentação estática de estados;

• diferenciar as saídas y até que uma entrada u apareça;

• escolher uma entrada de controle u de modo que as não-linearidades sejam canceladas e a convergência seja garantida durante o movimento de seguimento.

Aplicando este método ao modelo (10), deve-se diferenciar a saída j, obtendo:

O sistema resultante é singular e independe da entrada h₂. Isto indica que a linearização por realimentação estática para robôs não-holonômicos não é possível. Prossegue-se então aplicando a linearização por realimentação dinâmica de estados. Considerando o sistema 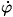= EU, adiciona-se integradores até que a matriz E seja invertível. Portanto, para se obter uma solução para o mesmo, é necessário utilizar uma expansão do modelo (Slotine and Li, 1991) da forma:

Dando prosseguimento ao procedimento de linearização do sistema através da realimentação dinâmica, deriva-se novamente o vetor de saída 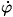, utilizando agora o modelo estendido, obtendo-se:

Esta matriz será invertível sempre que h₁¹ 0, ou seja, sempre que a velocidade do robô for diferente de zero. Se o sistema (15) for escrito de forma reduzida como = E.U, deseja-se determinar o valor de U que linearize o sistema, assim:

com = v indicando que o sistema está linearizado.

Considerando f_ref como a trajetória de referência a ser seguida pela função de saída j, e k₁ e k₂ ganhos de realimentação escolhidos de forma que o sistema resultante seja estável, então, utiliza-se um controlador auxiliar com a seguinte lei de controle:

onde = j – j_ref é o erro de convergência; portanto, este último terá a seguinte equação característica

em que os valores de k₁ e k₂ implicarão na velocidade de convergência até a trajetória desejada.

Compondo o modelo (10) com o vetor de entradas de controle, para resultar num modelo dependente das velocidades das rodas

₁ e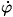 ₂, obtém-se o seguinte modelo para o robô móvel

O resultado da aplicação do sistema de rastreamento por linearização dinâmica pode ser visto na Figura 2, onde foram utilizados pólos rápidos (-20 e -21). Vê-se que o sistema converge rapidamente para a trajetória desejada. O ângulo de orientação inicial do robô foi de 3p/ 4. Observa-se ainda que apenas dois estados foram estabilizados (x, y), a orientação do robô (q) pode não ser a desejada, ou seja, o robô pode estar navegando para trás. Entretanto, pode-se estender os conceitos apresentados para o controle dos três estados.

Estabilização suave variante no tempo

A técnica apresentada no item anterior é de grande valia para seguir uma trajetória, não servindo para a estabilização numa configuração final. Para resolver este problema algumas técnicas foram desenvolvidas nos últimos anos, tais como: realimentação suave variante no tempo (Samson and Ait-Abderrahim, 1990) (idéia explorada inicialmente por Sontag and Sussmann (1980)) e realimentação contínua por partes (Bloch and McClamroch, 1989). O que se destaca entre estas duas técnicas é que a estratégia não contínua proporciona uma convergência exponencial e global para o ponto de equilíbrio, enquanto a primeira a convergência é assintótica mas não exponencial (Samson and Ait-Abderrahim, 1991). A técnica de "Backsteping" tem sido utilizada para obtenção de estabilização exponencial para sistemas não-holonômicos (Morin and Samson, 1996).

O método de realimentação suave e variante no tempo (Pomet, 1992) consiste de dois pontos básicos:

- Escolha de uma função variante no tempo a(t, x) que tenha as seguintes propriedades:

1. Seja periódica

2. Seja par

3. Se anule para x = 0

- Solução da seguinte equação diferencial para V, onde V é uma função candidata de Lyapunov:

com condição inicial em t = 0:

Para as condições impostas a a(t, x), garante-se que a função de Lyapunov será decrescente para o sistema em malha fechada que utilize o seguinte vetor de entradas:

Onde L_fg = Ñgf é o operador derivada de Lie e f e g são funções suaves.

Uma forma mais simples de se chegar à lei de controle é através do método simplificado (Pomet, 1992). Este é mais restrito em relação ao caso geral, mas quando aplicável oferece um modo mais fácil de se obter a função candidata de Lyapunov V(t, x), sem a necessidade de resolver qualquer relação diferencial, e assim obter a lei de controle (u₁, u₂, ¼, u_m). Ele se baseia na suposição de que existe um sistema de coordenadas (x₁, x₂, ¼, x_n) tal que,

Se esta condição for satisfeita para o sistema, então é sempre possível escolher uma função de Lyapunov V(t, x) da forma:

Impõem-se algumas condições sobre a função h, tal que, ao invés de se tomar a como parâmetro de projeto e resolver a equação diferencial para a função de Lyapunov V (equação (22)), toma-se h como parâmetro de projeto e calcula-se a função a para satisfazer (22), sendo V em (22) dada agora por (26). Para o robô em estudo, se a condição (25) for satisfeita, então para qualquer função h(t, x₂, x₃,¼, x_n) satisfazendo as seguintes condições:

a função de Lyapunov V dada por (26) e a função a dada por

são tais que as condições (19), (20), (21) e (22) são verificadas, e assim pode-se calcular a lei de controle (24).

Exemplo: O robô móvel KHEPERA (Pomet, 1992)

O modelo reduzido deste robô é dado por

Logo:

Como o determinante deste último sistema é igual a –1 tem-se que o posto é igual a 3 que é igual à ordem do sistema; portanto, o sistema é controlável. Tomando a função de Lyapunov da forma (26) para n = 3 e escolhendo a função h como:

h(t, x₂, x₃) = x₂ cos t,

as condições (27) e (28) são satisfeitas e V é dada por:

Determina-se, então:

L_f1V = ÑV f₁ = x₁ + x₂ cos t

L_f2V = ÑV f₂ = (x₁ + x₂ cost)x₁ cos t + x₁x₂ + x₃

e a função a é calculada como:

logo, o vetor de controle com realimentação de estados, suave e variante no tempo que estabiliza o sistema para a origem será:

Pomet (1992) utiliza a lei de estabilização que é aplicada ao robô KHEPERA , dada por:

Esta lei de controle foi obtida com a utilização de uma nova função de Lyapunov ligeiramente diferente da aqui proposta:

com a sendo uma constante real positiva e y uma função real suave com y¢ > 0 e y(q) = 0 para q = 0.

A Figura 3 mostra resultados de simulação utilizando esta estratégia. Observa-se que a trajetória é irregular e isto torna este tipo de controlador impraticável quando o estado inicial está longe do estado final. Adotou-se um tempo de 50 segundos de simulação. Mesmo com este tempo tão longo o robô não conseguiu atingir o estado final. Nota-se que nos instantes finas de simulação o robô oscila em direção à origem.

Em Pomet et al (1992) é realizada uma análise da influência dos parâmetros de projeto y(q) e . Verifica-se que para = 20 (um valor grande), a velocidade de convergência de (x, y) para (0, 0) é maior que para o caso = 1, e que para o caso de y(q) = q o movimento é errático e a trajetória apresenta maior número de "pontas" que para o caso de, por exemplo, y(q) = tan(q/ a), com a > 2.

Estabilização usando sinais não contínuos ou transformações não-lineares

Através da escolha adequada de um sistema de equações de estado (Aicardi et al., 1995), a utilização de funções de Lyapunov na forma quadrática leva ao projeto direto de leis de controle simples e suaves para o robô móvel com acionamento diferencial. O sistema utilizado é o representado pela equação (9) e a função candidata de Lyapunov é dada por:

Considerando que a derivada de V deve ser negativa e através de manipulações algébricas chega-se às seguintes leis de controle:

Um exemplo de veículo localizado em (x, y, q) = (–1, 1, 3p/4) em relação a base de referência é mostrado na Figura 4. O objetivo é atingir a origem (x, y, q) = (0,0,0). Utilizando coordenadas polares, as condições iniciais serão (e(0), a(0), f(0)) = (, –p, –p/ 4), foram aqui utilizados g = 3; h = 1; e k = 6.

A principal limitação deste controlador está na dificuldade de estender esses resultados (principalmente a representação em coordenadas polares) para sistemas com mais de três graus de liberdade, como veículos articulados, carros, etc. Entretanto o comportamento do sistema é bem superior ao de outras técnicas, produzindo uma resposta assintoticamente estável com um excelente tempo de acomodação.

Controladores híbridos

Tipicamente, controladores híbridos combinam características de continuidade no tempo com características a eventos discretos ou de tempo discreto. A operação de controladores híbridos é baseada no chaveamento em intervalos de tempo discreto entre diversos controladores contínuos no tempo. Os instantes de tempo nos quais o chaveamento pode ocorrer podem tanto ser especificados a priori quanto determinados no processo de operação do controlador Kolmanovsky and McClamroch, 1995).

Para projetar um controlador híbrido, Hespanha and Morse (1999) e Hespanha et al. (1999b) e partem do princípio de que todo sistema não-holonômico com três variáveis e duas entradas pode ser transformado no duplo integrador de Brockett. Assim, são propostos controladores híbridos empregando supervisão e chaveamento baseado em lógica discreta. Um controlador usando conceitos semelhantes também é proposto por Aguiar and Pascoal (2000) e aplicado a um robô móvel com acionamento diferencial. Piccoli et al. (1998) propõem um controlador híbrido empregando autômatos finitos que é estável no sentido de Lyapunov, e é projetado de maneira a garantir que os sinais de controle mantenham-se uniformemente limitados e tenham no máximo um número finito de descontinuidades em qualquer intervalo finito.

Um bom exemplo de controle híbrido para o robô com acionamento diferencial é dado por Bloch et al. (2000). A partir das equações transformadas para a forma de integrador de Brockett ou sistema de Heisenberg:

utilizam-se sinais de controle semelhantes a:

u = – ax + bzy v = – ax – bzx,

levando o sistema a assumir a forma

Se a função de energia for tomada como V = x² + y², então, sua derivada será = -2aV. Se inicialmente for escolhidos a = 0 e b > 0, então para x ou y diferentes de zero, z será levado assintoticamente a zero enquanto V permanecerá fixo. Se a > 0 e b = 0, então V será levado a zero.

O sinal de controle utilizado para estabilizar o robô móvel com acionamento diferencial tem a forma:

onde define-se [Y, x] = –[x, Y] º Yx.

O algoritmo de controle pode então ser assim descrito (com

_* denotando o maior autovalor Y^TY, x_* denotando a projeção de x sobre o auto-espaço de Y^TY, e Y_c denotando a projeção de Y sobre o espaço nulo de M(x); d estabelece a tolerância de erro):

início

enquanto ||Y|| > d

1. Com r = ||x||, implementar a lei de controle (32) com a = _*k, g = k e b = 0. Então Y evolui isoespectralmente com norma constante, enquanto x converge para a constante x_*. Se x_*¹ 0 ir para o passo 3.

2. Com z_* denotando um autovetor fixo

_* e ||z_*|| = r(1 – 1/ dim(m))^1/2, escolher u = - a(x – z_*), onde a > 0. Então x converge para z_* enquanto Y permanece constante.

3. Implementar a lei de controle (32) com a = g = 0, b < 0. Então x evolui isoespectralmente com norma constante, e Y converge para o valor constante Y_c.

fim enquanto

se ||x|| > d, então

4. implementar o controle (32) com a > 0, b = g = 0. Então x convergirá para zero radialmente, enquanto Y permanece em zero.

fim

O sistema descrito foi simulado a partir das condições iniciais x₁ = 1, x₂ = 1, q = 3*pi/4 e = = 1.5 , com os ganhos chaveados a cada 3 segundos conforme matriz abaixo:

A trajetória do sistema real obtida (x₁, x₂) e o comportamento dos estados transformados (x, y, z) podem ser vistos na Figura 5.

Os principais problemas de estratégias envolvendo o controle híbrido são: preservação da estabilidade após o chaveamento; instabilidade do chaveameamento (comutação intensa); e definição do instante onde deve ocorrer o chaveamento. Algumas estratégias utilizam tempo, distância (ou norma), regiões de operação, e superfícies (modos deslizantes) para determinar o instante de chaveamento. A verificação da estabilidade pode utilizar: função global de Lyapunov, múltiplas funções de Lyapunov, critério algébrico de estabilidade, passividade, etc. O desempenho do controlador dependerá da metodologia adotada, e as trajetórias dos estados podem não ser tão naturais quanto esperado.

7 CONCLUSÃO

Sistemas não-holonômicos constituem uma classe de sistemas com características especiais, impondo desafios ao desenvolvimento da teoria de controle. Nota-se que na fase de análise são utilizadas ferramentas da geometria diferencial. Isto fica transparente no projeto de controladores quando se empregam formas canônicas com propriedades de controlabilidade e atingibilidade já verificadas.

O projeto de leis de controle para malha fechada utiliza principalmente funções de Lyapunov. No início dos anos 90, os controladores sintetizados eram estáveis e assintoticamente estáveis, porém, o tempo para a convergência poderia ser estendido indefinidamente. A partir de 1995, foram desenvolvidas técnicas para a estabilização exponencial.

Quanto à estabilização num ponto de equilíbrio, o emprego da realimentação suave variante no tempo gera sistemas estáveis, mas sua trajetória tende a ser oscilatória. A realimentação não contínua tende a gerar trajetórias mais naturais. O controle híbrido ainda apresenta problemas para síntese de leis de controle exponencialmente estáveis e têm sido objeto de inúmeras contribuições nos últimos anos.

Como temas ainda em desenvolvimento e que requerem mais pesquisas, podem-se citar:

• projeto de sistemas robustos que considerem incertezas no modelo, sensores e na própria condição de não-holonomicidade;

• desenvolvimento de novas técnicas de projeto de sistemas de controle híbrido que gerem sistemas exponencialmente estáveis;

• emprego desta teoria na análise, projeto e controle de sistemas tolerantes a falhas;

• necessidade de novos avanços na teoria do controle geométrico e em ferramentas de geometria diferencial, facilitando a análise e projeto de sistemas de controle;

• desenvolvimento de sistemas de pilotagem automática que considerem as restrições não-holonômicas, melhorando a confiabilidade e estendendo o grau de automatismo de veículos terrestres, aquáticos e aeroespaciais.

No artigo foram apresentados os desenvolvimentos mais recentes e significativos por área e apresentada uma contribuição relativa à comparação de algumas técnicas de estabilização e áreas a serem desenvolvidas em futuros trabalhos assim como conceitos básicos fundamentais para entendimento do comportamento de sistemas não-holonômicos.

AGRADECIMENTOS

Este trabalho contou com o apoio parcial da FAPEMIG e da Fundação Geraldo Perligeiro de Abreu. Os autores gostariam de agradecer os revisores anônimos por seus excelentes comentários e sugestões.

REFERÊNCIAS

Agrachev, A. A. and Liberzon, D. (2001). Lie-algebraic stability criteria for switched systems, SIAM J. Control Optim. 40(1): 253{269.

Aguiar, A. P., Atassi, A. N. and Pascoal, A. M. (2000). Regulation of a nonholonomic dynamic wheeled mobile robot with parametric modeling uncertainty using lyapunov functions, Proc. of CDC 2000 - 39th IEEE Conference on Decision and Control - Sydney - Australia.

Aguiar, A. P. and Pascoal, A. (2000). Stabilization of the extended nonholonomic double integrator via logic-based hybrid control, Proc. of SYROCO-00 - 6th IFAC Symposium on Robot Control - Viena, Austria .

Aguiar, A. P. and Pascoal, A. M. (2001). Regulation of a nonholonomic autonomous underwater vehicle with parametric modeling uncertainty using lyapunov functions, Proceedings of 40th IEERE Conference on Decision and Control pp. 1 – 6.

Aguiar, A. and Pascoal, A. (1999). Stabilization of autonomous vehicles with nonholonomic constraints: Open problems and future directions, Proc. Workshop Future Directions in Systems and Control Theory - Cascais, Portugal .

Aicardi, M., Cannata, G., Casalino, G. and Indiveri, G. (2000a). Guidance of 3d underwater nonholonomic vehicle via projection on holonomic solutions, Symposium on Underwater Robotic Technology, Hawaii, USA .

Aicardi, M., Cannata, G., Casalino, G. and Indiveri, G. (2000b). On the stabilization of the unicycle model projecting a holonomic solution, 8th Int. Symposium on Robotics with Applications ISORA 2000, Hawaii, USA .

Aicardi, M., Casalino, G., Bicchi, A. and Balestrino, A. (1995). Closed loop steering of unicycle-like vehicles via lyapunov techniques, IEEE Robotics and Automation Magazine pp. 27{35.

Aicardi, M., Casalino, G. and Indiveri, G. (2000). On a closed loop time invariant position control solution for an uderactuated 3d underwater vehicle: implementation, stability and robustness considerations, Underwater Technology 2000, Tokio, Japan .

Aicardi, M., Casalino, G. and Indiveri, G. (2001). New techniques for the guidance of underactuated marine vehicles, 2001 IARP Workshop - Underwater Robotic for Sea Exploitation and Environmental Monitoring, Rio de Janeiro, Brazil .

Aicardi, M., Casalino, G., Indiveri, G., Aguiar, A., Encarnação, P. and Pascoal, A. (2001). A planar path following controller for underactuated marine vehicles, Proc. of MED 2001 - 9th IEEE Mediterranean Conference on Control and Automation, Dubrovnik, Croatia .

Antsaklis, P., Koutsoukos, X. and Zaytoon, J. (1999). On hybrid control of complex systems: a survey. Work supported by US National Science Foundation, US Army Research O ce and French Ministry of Research and Technology.

Arnol'd, V. I. and (Eds.), S. P. N. (1994). Dynamical Systems VII - Integrable Systems, Nonholonomic Dynamical Systems., Vol. 16 - No.VII of Encyclopaedia of Mathematical Sciences, translated from the russian edn, Springer-Verlag, New York.

Astol , A. (1999). Exponential stabilization of a wheeled mobile robot via discontinuous control, Journal of Dynamic Systems, Measurement and Control 121: 121{126.

Baluja, S. (1996). Evolution of an artificial neural network based autonomous land vehicle controller, IEEE Transactions on Systems, Man, and Cybernetics - Part B: Cybernetics 26(3): 450–463.

Bloch, A., Drakunov, S. and Kinyon, M. (2000). Stabilization of nonholonomic systems using isospectral ows, Research Report - University of Michigan .

Bloch, A. and McClamroch, N. H. (1989). Control of mechanical systems with classical nonholonomic constrains, Proceeding of 28th IEEE Conf. on Decision and Control - Tampa pp. 201–205.

Branicky, M. S. (1998). Multiple lyapunov functions and other analysis tools for switched and hybrid systems, IEEE Transactions on Automatic Control 43(4): 475–482.

Brockett, W. (1983). Asymptotic stability and feedback stabilization, in book: Differential geometric control theory - R.W. Brockett, R.S. Millman, and H.J.Sussmann pp. 181–191.

Bushnell, L. G., Tilbury, D. and Sastry, S. S. (1994). Extended goursat normal forms with applications to nonholonomic motion planning., Technical report, Electronics Research Laboratory, University of California at Berkeley.

Chang, Y.-C. and Chen, B.-S. (1996). Adaptive tracking control design of nonholonomic mechanical systems, Proceedings of the 35th Conference on Decision and Control pp. 4739–4744.

Chang, Y.-C. and Chen, B.-S. (2000). Robust tracking designs for both holonomic and nonholonomic constrained mechanical systems: Adaptive fuzzy approach, IEEE Transactions on Fuzzy Systems 8(1): 46–66.

Chwa, D. K., Seo, J. H., Kim, P. and Choi, J. Y. (2002). Sliding mode tracking control of nonholonomic wheeled mobile robots, Proceedings of the American Control Conference pp. 3991–3996.

Colbaugh, R., Barany, E. and Glass, K. (1998). Adaptive control of nonholonomic robotic systems, Journal of Robotic Systems 15(7): 365–393.

D'Andréa-Novel, B., Campion, G. and Bastin, G. (1995). Control of wheeled mobile robots not satisfying ideal velocity constraints: A singular perturbation approach, International Journal of Robust and Nonlinear Control 5: 243{267.

Decarlo, R. A., Branicky, M. S., Pettersson, S. and Lennartson, B. (2000). Perspectives and results on the stability and stabilizability of hybrid systems, Proceedings of the IEEE 99(7): 1069–1082.

Divelbiss, A. W. and Wen, J. T. (1997). A path space approach to nonholonomic motion planning in the presence of obstacles, IEEE Trans. on Robotics and Automation 13(3): 443–451.

Do, K. D. and Pan, J. (2002). Adaptive global stabilization of nonholonomic systems with strong nonlinear drifts, Systems & Control Letters 46: 195–205.

Dong, W. and Xu, W. L. (2001). Adaptive tracking control of uncertain nonholonomic dynamic system, IEEE Transactions on Automatic Control 46 (3): 450–454.

Dong, W., Xu, Y. and Huo, W. (2000). On stabilization of uncertain dynamic nonholonomic systems, International Journal of Control 73(4): 349–359.

Dubrovin, B., A.T.Fomenko and S.P.Novikov (1984). Modern Geometry - Methods and Applications, Vol. 1 of Springer Series in Soviet Mathematics, rst edn, Springer-Verlag, New York.

Fernandes, C., Gurvits, L. and Li, Z. (1994). Near-optimal nonholonomic motion planning for a system of coupled rigid bodies, IEEE Transactions on Automatic Control 39(3): 450–463.

Figueiredo, L. C. and Jota, F. G. (2002). A switching time-varying and time invariant controller to stabilize nonholonomic systems, CBA2002 - XIV Congresso Brasileiro de Automática pp. 2902–2907.

Fontes, F. A. C. C. (2002). Stabilizing nonholonomic systems by model predictive control, Officina Mathematica - Controlo 2002 - Universidade do Minho pp. 1–7.

Fucao, T., Nakagawa, H. and Adachi, N. (2000). Adaptive tracking control of a nonholonomic mobile robot, IEEE Transactions on Robotics and Automation 16(5): 609–615.

Fujimoto, K. and Sugie, T. (2001). Stabilization of hamiltonian systems with nonholonomic constraints based on time-varying generalized canonical transformations, Systems & Control Letters 44: 309–319.

Ge, S. S., Sun, Z., Lee, T. H. and Spong, M. W. (2001). Feedback linearization and discontinuous control of second-order nonholonomic chained systems, Proceedings of the 2001 IEEE International Conference on Control Applications pp. 990–995.

Ge, S., Wang, Z. and Lee, T. H. (2003). Adaptive stabilization of uncertain nonholonomic systems by state and output feedback, Automatica 39: 1451–1460.

Getz, N. H. (1994). Control of balance for a nonlinear nonholonomic non-minimum phase model of a bicycle., American Control Conference, Baltimore, American Automatic Control Council pp. 148–151.

Getz, N. H. and Marsden, J. E. (1995). Control for an autonomous bicycle., IEEE International Conference on Robotics an Automation - Nagoya. pp. 21–27.

Glass, K. and Colbaugh, R. (1997). Adaptive control of nonholonomic robotic systems for waste management applications, Technical Completion Report WERC-1-2-20575, New Mexico Waste-management Education and Research Consortium, Department of Mathematical Sciences - New Mexico State University.

Hespanha, J. P. (2001a). Toturial on supervisory control, 40th Conference on Decision and Control - Orlando, Florida Lecture Notes in Control using Logic and Switching: 1–46.

Hespanha, J. P. (2001b). UNESCO Encyclopedia of Life Support Systems, UNESCO, chapter Stabilization Through Hybrid Control, p. To appear.

Hespanha, J. P., Liberzon, D. and Morse, A. S. (1999a). Logic-based switching control of a nonholonomic system with parametric modeling uncertainty, Systems and Control Letters (special issue on hybrid systems 38: 167–177.

Hespanha, J. P., Liberzon, D. and Morse, A. S. (1999b). Supervision of integral-input-to-state stabilizing controllers, Proc. 5th European Control Conf. .

Hespanha, J. P., Liberzon, D. and Morse, A. S. (2001). Hysteresis-based supervisory control of uncertain linear systems.

Hespanha, J. P., Liberzon, D. and Morse, A. S. (2002). Hysteresis-based switching algorithms for supervisory control of uncertain systems, Submitted for publication in Automatica .

Hespanha, J. P. and Morse, A. S. (1999). Stabilization of nonholonomic integrators via logic-based switching, Automatica - Special Issue on Hybrid Systems 35: 385–393.

Hocherman-Frommer, J., Kulkarni, S. R. and Ramadge, P. J. (1998). Controller switching based on output prediction erros, IEEE Transactions on Automatic Control 43(5): 596–607.

Horiuchi, S. and Sunada, K. (1998). Synthesis of driver assistance system for lane-following using generalized predictive control, Proceedings of AVEC 98 pp. 467–472.

Hu, H., Gu, D. and M.Brady (1997). Navigation and guidance of an intelligent mobile robot., IEEE Trans. .... 8/97: 104–111.

Hunt, K. J., Haas, R. and Kalkkuhl, J. C. (1996). Local controller network for autonomous vehicle steering, Control Eng. Practice 4(8): 1045–1051.

Indiveri, G., Aicardi, M. and Casalino, G. (2000). Nonlinear time-invariant feedback control of an underactuated marine vehicle along a straight course, Proc. of the IFAC Conference on Manoeuvring and Control of Marine Craft, Aalborg, Denmark .

Janet, J. A., Gutierrez, R., Chase, T. A., White, M. W. and Sutton, J. C. (1997). Autonomous mobile robot global self-localization using kohonen and region-feature neural networks, Journal of Robotic Systems 14(4): 263–282.

Jiang, Z. and Nijmeijer, H. (1997). Tracking control of mobile robots: A case study in backstepping, Automatica 33(7): 1393{1399.

Jiang, Z. and Nijmeijer, H. (1999). A recursive technique for tracking control of nonholonomic systems in chained form., IEEE Transactions on Automatic Control 44(2).

Jiang, Z.-P. (2000). Robust exponential regulation of no-nholonomic systems with uncertainties, Automatica 36: 189–209.

Jiang, Z.-P. (2002). Global tracking control of underac-tuated ships by lyapunov's direct method, Automatica 38: 301–309.

Khalil, H. K. (1996). Nonlinear Systems, second edn, Prentice Hall, Upper Saddle River, NJ.

Kim, B. and Tsiotras, P. (2002). Controllers for unicycle-type wheeled robots: Theoretical results and experimental validation, IEEE Transactions on Robotics and Automation 18(3): 294–307.

Kolmanovsky, I. and McClamroch, N. H. (1995). Developments in nonholonomic control problems., IEEE Trans. On Control Systems pp. 20–36.

Kreyszig, E. (1991). Differential Geometry, reprint edn, Dover Publications Inc., New York.

Lafferriere, G. and Sussmann, H. J. (1991). Motion planning for controllable systems without drift., Proc. Int. Conf. Robotics and Automation - Sacramento, CA. pp. 1148–1153.

Latombe, J. C. (1993). Robot Motion Planning, Kluwer Academic Publishers, Boston.

Laumond, J., Jacobs, P. E. and Murray, R. M. (1994). A motion planner for nonholonomic mobile robots., IEEE Transactions on Robotics and Automation 10 (5).

Laumond, J.-P. (ed.) (1998). Robot Motion Planning and Control, Laboratoire d'Analye et d'Architecture des Systemes - Centre National de la Recherche Scientique - LAAS, chapter Guidelines in Nonholonomic Motion Planning for Mobile Robots, pp. 1–53.

Lefeber, E. and Nijmeijer, H. (1999). Adaptive tracking control of nonholonomic systems: an example, Proceedings of the 38th Conference on Decision and Control pp. 2094–2099.

Liberzon, D. and Morse, A. S. (1999). Basic problems in stability and design of switched systems, IEEE Control Systems Magazine 19: 59{70.

Lin, W., Pongvuthithum, R. and Qian, C. (2002). Control of high-order nonholonomic systems in power chained form using discontinuous feedback, IEEE Transactions on Automatic Control 47(1): 108–115.

Lizarralde, F. and Wen, J. T. (1996). Feedback stabilization of nonholonomic systems in presence of obstacles, IEEE Int. Conf. on Robotics and Automation - Minneapolis - MN pp. 2682–2687.

Lizarralde, F., Wen, J. T. and Hsu, L. (1999). A new model predictive control strategy for a ne nonlinear control systems, American Control Conference - San Diego - CA .

Luo, J. and Tsiotras, P. (1997). Exponentially convergent controllers for n-dimensional nonholonomic systems in power form, American Control Conference Albuquerque, NM .

Lygeros, J., Godbole, D. N. and Sastry, S. (1996). A verified hybrid controller for automated vehicles. Research supported by the PATH program, Institute of Transportation Studies, U.C. Berkeley.

Mahindrakar, A. D., Banavar, R. N. and Reyhanoglu, M. (2001). Discontinuous feedback control of a 3 link planar ppr underactuated manipulator, Proceedings of the 40th IEEE Conference on Decision and Control pp. 2424–2429.

McClamroch, N. H. and Kolmanovsky, I. (2000). Performance benefits of hybrid control design for linear and nonlinear systems, Proceedings of the IEEE 88(7): 1083{1096.

McClamroch, N. H., Rui, C. and Kolmanovsky, I. (1997). Hybrid closed loop systems: A nonlinear control perspective, Procedures of the 36th IEEE CDC - San Diego, CA. pp. 114–119.

M'Closkey, R. T. and Murray, R. M. (1997). Exponential stabilization of driftless nonlinear control systems using homogeneous feedback, IEEE Transactions on Automatic Control 42(5): 614–628.

Mirtich, B. and Canny, J. (1992). Using skeletons for nonholonomic path planning among obstacles., Proceedings of the IEEE International Conference on Robotics and Automation pp. 2533–2540.

Morin, P., Pomet, J.-B. and Samson, C. (1999). Design of homogeneous time-varying stabilizing control laws for driftless controllable systems via oscillatory approximation of lie brackets in closed loop, Society for Industrial and Applied Mathematics - SIAM - Control Optim. 38(1): 22–49.

Morin, P. and Samson, C. (1995). Time-varying exponential stabilization of the attitude of a rigid space-craft with two controls, Rapport de recherche 2493, Institut National de Recherche en Informatique et en Automatique, Sophia-Antipolis.

Morin, P. and Samson, C. (1996). Application of backs-tepping techniques to the time-varying exponential stabilization os chained form systems, Rapport de recherche 2792, Institut National de Recherche en Informatique et en Automatique, Sophia-Antipolis.

Morin, P. and Samson, C. (1997). Application of backs-tepping techniques to the time-varying exponential stabilisation of chained form systems, European Journal of Control 3: 15{36.

Morin, P. and Samson, C. (1998). Exponential stabilization fo nonlinear driftless systems with robustness to unmodeled dynamics, Rapport de recherche 3477, Institut National de Recherche en Informatique et en Automatique - INRIA, Sophia Antipolis - France.

Morin, P. and Samson, C. (2000a). A characterization of the lie algebra rank condition by transverse periodic functions, IEEE Conf. on Decision and Control (CDC) .

Morin, P. and Samson, C. (2000b). Control of nonlinear chained systems: From the routh-hurwitz stability criterion to time-varying exponential stabilizers, IEEE Transactions on Automatic Control 45 (1): 141–146.

Morin, P., Samson, C., Pomet, J.-B. and Jiang, Z.-P. (1994). Time-varying feedback stabilization of the attitude of a rigid spacecraft with two controls, Rapport de recherche 2275, Institut National de Recherche en Informatique et en Automatique, Sophia-Antipolis.

Morin, P., Samson, C., Pomet, J.-B. and Jiang, Z.-P. (1995). Time-varying feedback stabilization of the attitude of a rigid spacecraft with two controls, Systems and Control Letters 25: 375–385.

Murray, R. M., Li, Z. and Sastry, S. S. (1994). A mathematical introduction to robotic manipulation, 1st edn, CRC Press LLC.

Murray, R. M. and Sastry, S. S. (1993). Nonholonomic motion planning: Steering using sinusoids., IEEE Trans. On Automatic Control 38(5): 700–716.

Normey-Rico, J. E., Alcal a, I., Gomez-Ortega, J. and Camacho, E. F. (2001). Mobile robot path tracking using a robust pid controller, Control Engineering Practice 9: 1209–1214.

Piccoli, B., Pait, F. M. and Bittar, A. (1998). A hybrid controller for a nonholonomic system., SBA Controle e Automação 9(2).

Pomet, J. B. (1992). Explicit design of time-varying stabilizing control law for a class of controllable systems without drift, Systems and Control Letters 18: 147–158.

Pourboghrat, F. (2002). Exponential stabilization of nonholonomic mobile robots, Computers and Electrical Engineering 28: 349–359.

Pourboghrat, F. and Karlsson, M. P. (2002). Adaptive control of dynamic mobile robots with nonholonomic constraints, Computers and Electrical Engineering 28: 241–253.

Samson, C. (1990). Velocity and torque feedback control of a nonholonomic cart, Advanced Robot Control -Proceedings of the International Workshop on Nonlinear and Adaptive Control 162: 125–151.

Samson, C. (1992). Path following and time-varying feedback stabilization of a wheeled mobile robot, Proceedings Conf. ICASRCV 92 - Singapore pp. RO–13.1.1–RO–13.1.5.

Samson, C. (1995). Control of chained systems application to path following and time-vaying point-stabilization of mobile robots, IEEE Transactions on Automatic Control 40(1): 64–77.

Samson, C. and Ait-Abderrahim, K. (1990). Mobile robot control part 1: Feedback control of a nonholonomic wheeled cart in cartesian space, Programme 6 - Robotique, Image et Vision 1288, INRIA, Centre de Sophia-Antipolis, Sophia.

Samson, C. and Ait-Abderrahim, K. (1991). Feedback stabilization of a nonholonomic wheeled mobile robot, IEEE Int Workshop on Intelligent Robots and Systems - IROS 91 - Osaka, Japan .

Sanyal, A. K., Chellappa, M., Valk, J. L., Ahmed, J., Shen, J. and S.Bernstein, D. (2003). Globally convergent adaptive tracking of angular velocity with inertia identification and adaptive linearization, Proceedings of 13th IFAC Symposium on System Identification pp. 971{976.

Sekhavat, S. and Laumond, J.-P. (1998). Topological property for collision-free nonholonomic motion planning: The case of sinusoidal inputs for chained form systems, IEEE Transactions on Robotics and Automation 14(5): 671–680.

Shkel, A. M. and Lumelsky, V. J. (1997). The jogger's ploblem: Control of dynamics in real-time motion planning, Automatica 33(7): 1219–1233.

Slotine, J.-J. E. and Li, W. (1991). Applied Nonlinear Control, 1 st edn, Prentice Hall.

Sontag, E. D. and Sussmann, H. J. (1980). Remarks on continuos feedback, IEEE Conf on Decision and Control - Albuquerque.

Sordalen, O. J. and Egeland, O. (1995). Exponential stabilization of nonholonomic chained systems, IEEE Transactions on Automatic Control 40(1): 35–49.

Sun, D. and Hoo, K. A. (1999). Dynamic transition control structure for a class of siso nonlinear systems, IEEE Transactions on Control Systems Technology 7 (5): 622–629.

Sun, Z., Ge, S. S., Huo, W. and Lee, T. H. (2001). Stabilization of nonholonomic chained systems via non-regular feedback linearization, 44: 279–289.

Sussmann, H. (1993). A continuation method for nonholonomic path-finding problems., Proceedings of the 32nd IEEE Conference on Decision and Control, held in San Antonio pp. 2718{2723.

Sussmann, H. J. (1991). Optimal control and almost analytic feedback for some nonholonomic systems., Technical report, SYCON -Rutgers Center for Systems and Control, University of Rutgers.

Sussmann, H. J. (1992). New differential geometric methods in nonholonomic path finding., Systems, Models, and Feedback, A. Isidori and T.J. Tarn Eds.Birkäuser Boston, Inc. .

Sussmann, H. J. and Liu, W. (1997). Lie bracket extensions and averanging: The single-bracket case., Internal report, Department of Mathematics, Rutgers University.

Syam, R., Watanabe, K., Izumi, K. and Kiguchi, K. (2001). Adaptive actor-critic design using predictive model and its application to nonholonomic mobile robots, Proc. of the Fifth Intl. Conf. on KES 2001 pp. 1319–1324.

Syam, R., Watanabe, K., Izumi, K. and Kiguchi, K. (2002). Control of nonholonomic mobile robot by an adaptive actor-critic method with simulated ex- perience based value-functions, Technical report, Department of Advanced Systems Control Engineering - Saga University, Saga - Japan.

Tanner, H. G. and Kyriakopoulos, K. J. (2002). Discontinuous backstepping for stabilization of nonholonomic mobile robots, Proceedings of the 2002 IEEE International Conference on Robotics & Automation pp. 3948–3953.

Tayebi, A. and Rachid, A. (2000). Adaptive controller for nonholonomic mobile robots with matched uncertainties, Advanced Robotics 14(2): 105–118.

Tayebi, A., Tadjine, M. and Rachid, A. (2001). Invariant manifold approach for the stabilization of nonholonomic chained systems: Application to a mobile robot, Nonlinear Dynamics 24: 167–181.

Tian, Y.-P. and Li, S. (2002). Exponential stabilization of nonholonomic dynamic systems by smooth time-varying control, Automatica 38: 1139–1146.

Tilbury, D. and Chelouah, A. (1993). Steering a three-input nonholonomic system using multi-rate controls., IEEE Proceedings of the European Control Conference, Groningen, The Netherlands .

Tilbury, D., Sordalen, O., Bushnell, L. and Sastry, S. S. (1993). A multi-steering trailer system: Conversion into chained form using dynamic feedback., Technical Report M93/55, Electronics Research Laboratory, University of California at Berkeley.

Victorino, A. C. (1998). Controle de trajetória e estabilização de robôs móveis não-holonômicos, Master's thesis, Universidade Estadual de Campinas - Faculdade de Engenharia Mecânica, Campinas - SP.

Walsh, G., Tilbury, D., Sastry, S., Murray, R. and Laumond, J. P. (1994). Stabilization of trajectories for systems with nonholonomic constraints, IEEE Transactions On Automatic Control 39: 216–222.

Wen, J. (1996). Control of Nonholonomic Systems, in The Control Handbook, Ed. W.S. Levine - CRC Press.

Y-Kuc, T., Baek, S. M. and Park, K. (2000). Adaptive learning controller for autonomous mobile robots, IEE Proceedings Control Theory Appl. 148(1): 49–54.

Yang, J. and Kim, J. (1999a). Sliding mode motion control of nonholonomic mobile robots., IEEE Control Systems 19(2).

Yang, J.-M. and Kim, J.-H. (1999b). Sliding mode control for trajectory tracking of nonholonomic wheeled mobile robots, IEEE Transactions on Robotics and Automation 15(3): 578{587.

Ye, H., Michel, A. N. and Hou, L. (1998). Stability theory for hybrid dynamical systems, IEEE Transactions on Automatic Control 43(4): 461–474.

Artigo submetido em 23/08/01

1a. Revisão em 25/03/03, 2a. Revisão em 10/11/03

Aceito sob recomendação do Ed. Assoc. Prof. Liu Hsu

Datas de Publicação

• Publicação nesta coleção
  22 Nov 2004
• Data do Fascículo
  Set 2004

Histórico

• Revisado
  10 Nov 2003
• Recebido
  23 Ago 2001