Localização, modelagem e controle de um mini-helicóptero em ambientes internos

Localization, modelling, and control of a mini-helicopter in indoor environments

ROBÓTICA

Localização, modelagem e controle de um mini-helicóptero em ambientes internos

Localization, modelling, and control of a mini-helicopter in indoor environments

Marco Aurélio G. Moreira^I; Leonardo A. B. Tôrres^II; Guilherme A. S. Pereira^III; Paulo Iscold^IV

^IDepartamento de Engenharia Elétrica; magm@ufmg

^IIDepartamento de Engenharia Eletrônica; [e-mail]

^IIIDepartamento de Engenharia Elétrica; [e-mail]

^IVDepartamento de Engenharia Mecânica, Grupo de Pesquisa e Desenvolvimento de Veículos Autônomos, Universidade Federal de Minas Gerais, Av. Antônio Carlos, 6627, 31270-901, Belo Horizonte, MG, Brasil; [e-mail]

RESUMO

Este trabalho aborda o problema de robotização de um helimodelo comercial de pequeno porte para operação em ambientes internos. A solução para o problema é dividida em três subtarefas: (i) projeto e implementação de algoritmos de localização, (ii) desenvolvimento da modelagem do helimodelo e (iii) projeto e implementação de leis de controle. Para localização, propõe-se a combinação de informações provenientes de um sistema de visão estéreo e de sensores inerciais via Filtragem de Kalman. Os estados estimados, que compreendem posições e velocidades lineares e angulares, são usados em conjunto com os sinais de comando do piloto para estimar, por meio de métodos de identificação, os parâmetros de um modelo caixa-cinza. De posse do modelo dinâmico do helimodelo, são projetados os controladores, que consistem em controladores PID clássicos em cascata. Resultados experimentais mostram a estabilização de todos os graus de liberdade do helimodelo.

Palavras-chave: Robótica Aérea, helicópteros autônomos, veículos aéreos não tripulados.

ABSTRACT

This work addresses the robotization of a small-scale commercial helicopter. The solution involves three subtasks: (i) design and implementation of algorithms for localization, (ii) development of the helicopter model, and (iii) design and implementation of control laws. For localization, the combination of a stereo vision system and inertial sensors information via Kalman Filtering is proposed. The estimated states, which are linear and angular positions and velocities, along with the pilot commands are used to estimate, through system identification methods, the parameters of a gray box model. This model is further used to design the system controllers, which are traditional PID cascade control. Experimental results show the stabilization of all degrees of freedom of the mini-helicopter.

Keywords: Aerial Robotics, autonomous helicopters, unmanned aerial vehicles.

1 INTRODUÇÃO

Durante os últimos 20 anos, a pesquisa no desenvolvimento de helicópteros autônomos tem se mostrado bastante ativa. Em 1991, foi criada a IARC (International Aerial Robotics Competition). Organizada anualmente, esta competição constitui-se de missões que exigem de seus competidores o projeto e implementação de robôs com comportamentos ainda não demonstrados até então por nenhum veículo aéreo conhecido (IARC, 2010). Os desafios da IARC motivaram o aparecimento de diversos grupos de pesquisa em VANTs, muitos dos quais utilizando helicópteros como plataforma (Castillo-Effen et al., 2007).

Muito além de simplesmente atender aos requisitos da IARC, a pesquisa em helicópteros autônomos tem sido bastante diversificada. O uso desses veículos tem sido estudado para pulverização de lavouras, inspeção de sistemas de transmissão de energia, monitoração de atividade vulcânica, fotografia aérea, entre outras (Nonami, 2007).

Apesar de no contexto mundial a pesquisa em helicópteros autônomos estar bastante avançada, chegando inclusive ao estágio de acrobacias autônomas (Coates et al., 2008), poucos resultados experimentais foram demonstrados em território brasileiro. Um empreendimento de grande relevância foi o projeto HELIX (Gyron, 1998), na década de 1990, conduzido pela empresa Gyron em parceria com a Universidade Federal de Santa Catarina (UFSC) e o Centro de Tecnologia da Informação Renato Archer (CTI, então CenPRA), cujo objetivo era o desenvolvimento de um helicóptero autônomo para aplicações civis. Mais recentemente, resultados de destaque também têm sido alcançados em projetos na Universidade de Brasília (UnB) (Martins et al., 2007), Universidade Federal do Rio de Janeiro (UFRJ) (dos Santos, 2008) e Universidade Federal do Espírito Santo (UFES) (Brandão et al., 2010). No entanto, pelo conhecimento dos autores deste artigo, nenhum desses trabalhos apresentou experimentalmente a estabilização automática de todos os graus de liberdade de um helicóptero.

Pela complexidade das etapas necessárias a um voo autônomo, muitos projetos são encerrados precocemente. Neste trabalho, busca-se uma forma de facilitar e acelerar os testes de controle automático de um mini-helicóptero. Para tanto, é feita a opção por se trabalhar em ambientes internos. Essa escolha tem como vantagens, entre outras, a eliminação de perturbações por vento e o fato de não requerer deslocamento de pessoal e equipamento para a realização de experimentos. Embora possa ser menos útil do ponto de vista de aplicações, essa opção facilita o estudo do veículo.

O objetivo do trabalho é desenvolver um sistema robótico para operações em ambientes internos a partir de uma plataforma comercial de helimodelo. Considerando a tarefa de um voo autônomo, podemos dividir o problema em algumas etapas essenciais: (i) localização; (ii) obtenção de um modelo dinâmico; (iii) controle de posicionamento (ou velocidade); e (iv) planejamento de movimentos. Essas etapas são geralmente complexas e têm sido, individualmente, temas de pesquisa. Além disso, por diversos fatores, entre os quais a instabilidade do veículo em malha aberta, existe uma interdependência entre elas. A Figura 1 mostra como essa interdependência é considerada neste trabalho. As linhas mais espessas indicam fluxo de informações importantes para o desenvolvimento dos blocos aos quais estão conectadas. Os fluxos de sinais são representados pelas linhas menos espessas. Em cinza, são destacados os blocos para os quais este trabalho apresenta contribuições.

Assim, como destacado na Figura 1, as etapas apresentadas neste artigo são: localização, modelagem do veículo e controle automático. As metodologias utilizadas em cada uma delas são apresentadas, respectivamente, nas seções 2, 3 e 4. Resultados experimentais são apresentados na Seção 5. Por fim, na Seção 6 apresentam-se as conclusões e propostas de trabalhos futuros.

2 LOCALIZAÇÃO

A localização do helicóptero é fundamental nas etapas de modelagem e controle. Por isso, os estados a serem estimados foram escolhidos de tal forma a atender aos requisitos mínimos dessas etapas. Nesse sentido, procurou-se estimar o conjunto mínimo de variáveis que descrevem o movimento do helicóptero como o de um corpo rígido: posições e velocidades lineares e angulares. Como não existe um único sensor capaz de fornecer todas essas estimativas, foi adotada a estratégia de fusão sensorial, via filtragem de Kalman. Uma introdução sobre o assunto é apresentada em (Aguirre, 2007).

O Filtro de Kalman é uma solução bastante conhecida para o problema de combinação sensorial. A metodologia foi proposta em 1960 para estimação de estados de sistemas lineares em tempo discreto (Kalman, 1960). Para este propósito, o filtro é a solução ótima sob o critério de minimização da variância dos erros das estimativas. Neste trabalho, utiliza-se o Filtro de Kalman Estendido (EKF), que é uma adaptação para a estimação de estados de sistemas não-lineares.

Seja um sistema não-linear da forma:

em que w e v são variáveis aleatórias independentes, de média nula e com propriedades E[w_k]= M_k e E[v_k] = N_k¹. A variável w é chamada de ruído de processo e v, ruído de medição. As funções ƒ e h representam, respectivamente, os modelos de processo e de medição. O problema a ser solucionado pelo EKF consiste em obter, ∀k> 0, uma estimativa _k dos estados, dados os modelos ƒ e h, as condições iniciais x₀ e sua matriz de covariância , a sequência das entradas µ_k² e as medições y_k.

O algoritmo se divide basicamente em dois passos: predição e correção, e pode ser resumido por:

enquanto não atingir condição de parada

Predição

se há nova medição

Correção senão

fim se

fim enquanto,

em que , e são, respectivamente, estimativas que o filtro guarda de E[(x_k – _k|k–1)(x_k – _k|k–1)^T], E[(x_k – _k|k–1)(y_k – _k|k–1)^T] e E[(y_k – _k|k–1)(y_k – _k|k–1)^T]. No contexto da filtragem de Kalman, a grandeza y_k – _k|k–1 é conhecida como inovação. Dessa forma, P^yy é a estimativa da matriz de covariância da inovação.

A instanciação do Filtro de Kalman para um problema de combinação sensorial específico exige: (i) definição do modelo de processo, utilizado na etapa de predição; (ii) definição do modelo de medição, utilizado na etapa de atualização; e (iii) sintonia, que é o procedimento pelo qual são estimadas as matrizes de covariância M e N. Esses procedimentos são detalhados, respectivamente, nas subseções 2.1, 2.2 e 2.3.

2.1 Modelo de Processo

O movimento da aeronave, tratada como um corpo rígido, pode ser descrito por 12 variáveis: a posição p_NED = [N ,E ,D]^T, representada no referencial inercial {NED}³ , a velocidade v_ABC =[U, V, W]^T, representada no referencial {ABC}⁴ do helicóptero, a posição angular Φ = [Φ, θ, ψ]^T(rolamento, arfagem e guinada) e a velocidade angular ω_ABC =[P, Q, R]^T, representada no referencial da aeronave. Na abordagem deste trabalho, consideram-se como estados os vetores p_NED, v_ABC e Φ. As velocidades angulares são entradas para o modelo cinemático, bem como a aceleração linear a_ABC =[a_x,a_y ,a_z]^T. Dessa forma, o vetor de estados contém nove variáveis, x =[, , Φ^T]^T, e o vetor de entradas, que é lido de uma unidade de medição inercial (IMU)⁵, é dado por µ =[, ]^T

Em tempo contínuo, o modelo de propagação dos estados, = ƒ(x, µ), pode ser escrito como (Stevens and Lewis, 1992):

em que é a matriz de rotação entre os referenciais {ABC} e {NED},

e s e c são abreviações para as funções seno e cosseno, respectivamente.

Nas implementações computacionais, as derivadas na Equação (1) são aproximadas por = (x_k – x_k–1)/T_s, em que T_s é o período de amostragem. Além disso, cada equação cinemática de propagação, em tempo discreto, é corrompida por um ruído aditivo de processo T_sw_i, 1 < i < 9.

2.2 Modelo de Medição

Neste trabalho, as medições y são fornecidas por um sistema de visão estéreo. O termo "visão estéreo" se refere à habilidade de se inferir informação tridimensional de uma cena a partir de duas ou mais imagens obtidas de diferentes pontos de vista. Para tanto, são necessárias, usualmente, as seguintes etapas (Trucco and Verri, 1998): calibração das câmeras, retificação das imagens, cálculo das correspondências e reconstrução 3D.

A calibração é responsável pelo cálculo de parâmetros intrínsecos e extrínsecos. Para o modelo "buraco de agulha" (pinhole), adotado neste trabalho, os parâmetros intrínsecos mais importantes compreendem a distância focal F, tamanho efetivo dos píxeis s_x e s_y e coordenadas do centro da imagem c_x e c_y de cada câmera (ver Figura 2), além dos coeficientes de distorção das lentes. Por sua vez, os parâmetros extrínsecos indicam a posição e orientação relativas entre as câmeras, que podem ser representadas pela matriz de rotação e pelo vetor de translação T. Neste trabalho, para efeito de notação, um ponto P =(X, Y, Z) no espaço 3D tem projeção no ponto p no plano de imagem, cujas coordenadas descritas no referencial da imagem são ^Ip =(x_I ,y_I) e são expressas em píxeis. No referencial da câmera, ^Cp =(x, y, F), em que F é a distância focal da câmera. Definindo-se as grandezas ƒ_x = F/s_x e ƒ_y = F/s_y, pode-se verificar que:

x_I = ƒ_x(X/Z)+ c_x , y_I = ƒ_y (Y/Z) + c_y.

A metodologia de calibração de câmera consiste em apontar a câmera para uma estrutura conhecida que tem diversos pontos identificáveis. Ao visualizar essa estrutura de diversos ângulos, é possível computar a posição e orientação da câmera em cada imagem, assim como obter seus parâmetros intrínsecos. O alvo utilizado neste trabalho é similar a um tabuleiro de xadrez e o algoritmo de calibração é o mostrado em (Bradski and Kaehler, 2008). A calibração fornece os parâmetros intrínsecos das duas câmeras — ƒ_x, ƒ_y, c_x, c_y e coeficientes de distorção — e também a matriz de transformação homogênea que as localiza uma em relação à outra.

A retificação é o processo de reprojeção dos planos de imagem das duas câmeras de tal forma que as linhas das imagens resultantes estejam alinhadas. Nesse processo, as câmeras são alinhadas matematicamente, ao invés de fisicamente. A busca por correspondências, que determina pares de pontos (

_L e _R) nas imagens do sistema estéreo que representam um mesmo ponto P da cena (ver Figura 2), em imagens retificadas, se restringe à busca por pontos similares nas linhas correspondentes das imagens.

Para a localização do helicóptero, as correspondências são feitas entre apenas três pontos, que são as projeções nos planos de imagem de cada câmera de três marcos visuais coloridos afixados ao helicóptero. Por se trabalhar com poucos pontos, optou-se por não retificar as imagens. A identificação das cores é feita no espaço de cores YCrCb, em que a componente Y provê informação de luminância e as componentes Cr e Cb dão informação de crominância (Poynton, 2003). Na binarização de cada cor, um píxel é definido como ativo se e somente se suas componentes estão dentro de um conjunto de retângulos tridimensionais no espaço de cores. Estes são dimensionados empiricamente de forma a aproximar por partes o caminho feito pelas componentes Y, Cr e Cb à medida que se variam os parâmetros da cena, como iluminação e proximidade de outros objetos. A obtenção da posição de cada marco visual é feita por análise padrão de regiões (blobs) nas imagens binarizadas (Gonzalez and Woods, 2001).

Se os parâmetros intrínsecos e extrínsecos do sistema estéreo são conhecidos, a reconstrução 3D é direta (Trucco and Verri, 1998). Conforme mostrado na Figura 3, assuma que o ponto ^I

_L, par do ponto ^I

_R, tenha sido determinado. De posse dos parâmetros intrínsecos das câmeras, determinam-se os vetores unitários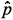 _L e 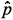_R, cujos prolongamentos teoricamente se interceptam. No entanto, dado que na prática os parâmetros de calibração e a localização das correspondências só são conhecidos aproximadamente, os raios O_L

_L e O_R

_R dificilmente se cruzam. O ponto de interseção é estimado, então, como o ponto de mínima distância entre os dois raios, que é o ponto médio do segmento perpendicular a ambos (Trucco and Verri, 1998).

O conhecimento da posição tridimensional dos três marcos visuais determina a pose (posição e orientação) do conjunto de marcos em relação ao referencial das câmeras. Como os marcos visuais são afixados em posições conhecidas no helicóptero e porque o posicionamento das câmeras é conhecido no referencial inercial {NED}, o sistema estéreo fornece, após algumas transformações de coordenadas, as posições

_N, _E, _D e os ângulos Φ, θ e ψ.

Os três marcos visuais definem um sistema de coordenadas {M}, conforme mostrado na Figura 4, no qual suas posições ^MP₀, ^MP₁ e ^MP₂ são conhecidas. O sistema de visão computacional estima a posição dos marcos, ^LP₀, ^LP₁ e ^LP₂ no sistema de coordenadas {L}, afixado à câmera da esquerda, através de que é possível obter a matriz de trans formação homogênea . Sejam os vetores dx, dy e dz dados por:

dx = 1/2 (^LP₁ + ^LP₂) dz = ( ^LP₁ – ^LP₀) × ( ^LP₂ – ^LP₀) dy = dz × dx.

Tomando os vetores unitários correspondentes —, e —, obtemos:

Finalmente, a localização do veículo em relação a {NED} é dada pela matriz de transfomação homogênea:

da qual se extraem os valores de

_N, _E, _D, Φ, θ e ψ. Assim,o modelo de medição é linear e tem a forma:

Vale mencionar que, matematicamente, os valores dos estados que representam ângulos não são univocamente determinados pelas coordenadas em píxeis dos marcos visuais na imagem devido a periodicidade em 2π da representação matemática dos ângulos. Por isso, optou-se por se resolver completamente o problema de localização por visão, escolhendo o intervalo desejado da solução, e em seguida apresentar o resultado como saída do modelo de medição.

O modelo de medição escolhido é interessante ainda por manter as mesmas equações do filtro para marcos visuais quaisquer, desde que o sistema de medição em questão seja capaz de estimar a pose completa do veículo. Assume-se que o ruído de medição atue em (2) de forma aditiva.

2.3 Sintonia do Filtro de Kalman

Para sistemas lineares, a Filtragem de Kalman é ótima, no sentido de minimizar a variância do erro de estimação. No entanto, para que se atinja a optimalidade, é necessário o conhecimento das matrizes de covariância de processo, M, e de covariância de medição, N. Usualmente, pode-se obter a matriz de covariância do ruído de medição com certa facilidade, a partir do conhecimento das incertezas padrão e expandidas associadas aos instrumentos de medição, mediante análise estatística dos sinais medidos em condição estacionária. Para se obter a matriz M, por sua vez, é necessário verificar de alguma maneira a confiança a ser depositada no modelo de propagação dos estados. Neste trabalho, isso foi feito com base nos três critérios para teste de consistência de um filtro definidos em (Bar-Shalom et al., 2001) para o caso linear e Gaussiano:

1. Os erros de estimação de estado devem ser aceitáveis como de média zero e devem ter magnitude em concordância com a matriz de covariância estimada pelo filtro;

2. As inovações devem apresentar as mesmas propriedades, ou seja, média zero e magnitude consistente;

3. As inovações devem ser aceitáveis como brancas.

Observa-se que somente os dois últimos critérios podem ser testados com dados reais. A sintonia do filtro levou em conta tais critérios. Fixada a matriz de covariância do ruído de medição, ajustaram-se os elementos da diagonal de M para que a variância das inovações fosse consistente com a matriz de covariância das inovações estimada pelo filtro e para que as inovações fossem descorrelacionadas no tempo.

Os estados estimados pelo sistema de localização foram utilizados, em conjunto com os sinais de comando do helicóptero, para estimar os parâmetros de um modelo dinâmico para o veículo. Além disso, foram usados também no ramo de realimentação do sistema de controle.

3 MODELAGEM

Para conduzir o helicóptero, o piloto dispõe de um conjunto u de 4 comandos: u_lat, que movimenta o helicóptero lateralmente; υlon, que controla o movimento longitudinal; u_ped, que atua no movimento de guinada; e u_col, responsável pelo movimento vertical. A modelagem consiste em encontrar equações matemáticas que expliquem como u influencia a evolução temporal dos estados. Frequentemente, o helicóptero é tratado como um corpo rígido (Béjar et al., 2007), cujas entradas são forças e torques e cujas saídas são p_NED, v_ABC, Φ e ω_ABC. As equações diferenciais que regem a evolução das posições lineares e angulares (Equação (1)), apesar de não-lineares, são bem conhecidas e não dependem de parâmetros. Assim, a modelagem se resume em encontrar uma relação representativa entre as entradas de fato controladas pelo piloto, u =[u_lat, u_lon, u_ped, u_col]^T, e as velocidades lineares e angulares.

Dada a grande quantidade de variáveis de entrada e de saída, é imprescindível que se use algum conhecimento do processo na modelagem. No entanto, o modelo completo, incluindo a flexibilidade dos rotores e fuselagem, escoamento do ar através das pás, dinâmica dos atuadores, etc., é extremamente complexo. Assim, comumente tenta-se explicar o comportamento dos helicópteros por modelos caixa-cinza.

A estrutura do modelo depende do propósito a que ele se destina. Modelos cuja finalidade seja projeto de controladores são geralmente simples. Nessa linha, um dos trabalhos mais importantes e citados na literatura é apresentado em (Mettler et al., 1999). O mérito dos autores está em encontrar um modelo linear, com representação em espaço de estados, parametrizado e reduzido que explica as características mais importantes da dinâmica de helicópteros em escala miniaturizada.

Com o objetivo de gerar modelos ainda mais simples, alguns autores propõem mapeamentos algébricos entre as entradas u e as forças e torques que atuam sobre o veículo. Essa é a estratégia utilizada em (Kondak et al., 2007), trabalho que tenta aproveitar as similaridades entre modelos de veículos da classe VTOL (Vertical Take-Off and Landing) para construir um modelo geral. O mapeamento algébrico é também a solução proposta em (Abbeel et al., 2006). Esse modelo se diferencia dos demais por fazer predição das acelerações do helicóptero, as quais são utilizadas posteriormente para atualização de velocidades. Pela simplicidade de suas equações, o modelo talvez não recebesse muita atenção não fossem os resultados publicados em (Coates et al., 2008). Nesse trabalho, manobras acrobáticas são conduzidas por controladores automáticos sintonizados com base na linearização local do modelo de Abbeel et al. (2006). Essas manobras exploram uma propriedade importante do modelo: ele é válido para atitudes arbitrárias. Pela simplicidade e por sua demonstrada capacidade de representar suficientemente bem a dinâmica de helicópteros no projeto de controladores, decidiu-se por adotar o modelo de Abbeel na modelagem do helicóptero do presente trabalho. O modelo é descrito pelas equações:

e

Nas Equações (3), (g_x)_k, (g_y)_k e (g_z)_k são a projeção da aceleração da gravidade em cada um dos eixos da aeronave no instante k; α_x = , α_y = e α_z = denotam acelerações angulares; a_x = , a_y = e a_z = são acelerações lineares; e C e D são parâmetros do modelo. As constantes D₁, D₂, D₃ e D₄ são utilizadas para modelar o ponto de operação das entradas de controle; o termo D₀ representa a força lateral — considerada constante — produzida pelo rotor de cauda. Nas Equações (4), é a matriz que indica a rotação da aeronave entre os instantes de tempo k e k +1, a_ABC = [a_x,a_y, a_z]^Te α_ABC =[α_x, α_y, α_z]^T.

O modelo anterior é uma representação parametrizada e linear nos parâmetros. A essa classe de modelos podem ser aplicados o método de Mínimos Quadrados (MQ) e suas variações. Neste trabalho, foram testadas, além do MQ, as estensões Mínimos Quadrados Ponderados (MQP) e LearnLagged-Acceleration (LLA). O MQP foi utilizado para se aproveitar a covariância estimada das medições de velocidades lineares, fornecida pelo Filtro de Kalman. O algoritmo LLA é uma extensão do MQ específica para as equações (3) e (4). O algoritmo mimiza o erro de predição num horizonte de H iterações, em que H é um parâmetro (Abbeel et al., 2006).

O helicóptero utilizado neste trabalho é um sistema instável em malha aberta. Dessa forma, a estimação de parâmetros deve ser feita em malha fechada, o que gera algumas dificuldades: (i) se a coleta dos sinais de saída for feita pelos mesmos sensores usados na realimentação, pode haver polarização dos parâmetros, devido à correlação entre entradas e ruídos de medição; (ii) é necessário que se tenha um controlador, que é difícil de projetar sem que haja um modelo dinâmico do veículo; (iii) os sinais de entrada não podem ser arbitrariamente escolhidos e, por isso, podem não apresentar persistência de excitação suficiente. A metodologia experimental adotada neste trabalho contorna as dificuldades (i) e (ii): os experimentos de identificação de parâmetros são feitos coletando-se dados de voos conduzidos por um piloto experiente. A maior dificuldade passa a ser gerar persistência de excitação. Mesmo para pilotos experientes, não é tarefa simples excitar as quatro entradas do veículo e ao mesmo tempo manter sua estabilidade.

A próxima seção apresenta como controladores são projeta-dos a partir do modelo obtido.

4 CONTROLE

Uma das causas de não linearidades no controle de helicópteros se deve ao fato de que o veículo obedece a comandos em seu sistema de coordenadas local, o referencial {ABC}, e as referências de posição são dadas num referencial global, o referencial {NED}. O mapeamento entre velocidades de {NED} para {ABC} é feito por uma matriz de rotação, que depende dos ângulos de atitude da aeronave (em voos não agressivos, essencialmente do ângulo de guinada). Embora as equações de mapeamento sejam não lineares, elas são bem conhecidas e não dependem de parâmetros. Dessa forma, as não linearidades podem ser compensadas por linearização por realimentação não-linear de estados. As duas estratégias de controle testadas neste trabalho adotam essa técnica.

4.1 Controlador 1: Atitude e Posição Horizontal em Cascata

As equações do modelo de Abbeel et al. (2006) (Equações (3)) indicam as principais relações entre os estados e as entradas do helicóptero. Altura e ângulo de guinada são controlados, respectivamente, por u_col e u_ped. Para a movimentação no plano

_ABC, manipula-se a projeção da gravidade nos eixos _ABC e 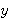_ABC, o que é equivalente a manipular os ângulos Φ e θ. Por fim, u_lat e u_lon são utilizados para controlar, respectivamente, Φ e θ. Com base nessas relações de causalidade, propõe-se a topologia de controle mostrada na Figura 5. Nessa figura, p_NE =[p_N, p_E, 0]^T, 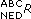(ψ) é a matriz de rotação que transforma o erro de posição horizontal do sistema {NED} para {ABC} e 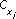indica o controlador monovariável da variável x_i.

4.2 Controlador 2: Atitude, Velocidade e Posição Horizontais em Cascata

O principal problema do Controlador 1 é não haver controle sobre as velocidades. Dessa forma, ao se realizarem grandes variações na referência de posição, mesmo com saturação na referência dos ângulos, é provável que o sistema de controle imprima altas velocidades ao veículo. Isso pode tirar o helimodelo do ponto em torno do qual foi levantado o modelo e, por consequência, levá-lo à instabilidade. Além disso, no caso de movimentação em ambientes internos, como é o caso dos testes deste trabalho, o risco de colisões é elevado.

Para superar essas limitações, foram adicionadas ao diagrama da Figura 5 malhas de controle para as velocidades U e V. A topologia de controle resultante é mostrada na Figura 6. De forma similar ao que ocorre no Controla-dor 1, o erro de posição no plano

_NED é rotacionado para o referencial do helicóptero. Para controlá-lo em {ABC}, manipulam-se as velocidades U e V, cujo controle é, por sua vez, realizado pela manipulação dos ângulos de arfagem e rolamento, controlados por u_lon e u_lat, respectivamente.

Os controladores monovariáveis mostrados nas figuras 5 e 6, que são do tipo PID (Proporcional-Integral-Derivativo), foram sintonizados em alguns casos por síntese direta e em outros empiricamente. O método de sintonia por síntese direta consiste em escolher os parâmetros do controlador para que se obtenha uma resposta desejada em malha fechada a uma entrada conhecida. Este método é apresentado com mais detalhes em (Seborg et al., 2003).

5 RESULTADOS EXPERIMENTAIS

Nesta seção, mostram-se os resultados experimentais das metodologias de localização, modelagem e controle.

5.1 Arranjo Experimental

O helicóptero utilizado neste trabalho é o modelo Honey Bee King II. Este helimodelo pesa aproximadamente 500 gramas e a helice de seu rotor principal mede 60 centímetros. Ele foi instrumentado como mostrado na Figura 7. A IMU utilizada é do modelo 3DM-GX1, fabricada pela Microstrain, que opera a 76 Hz e fornece, via cabo, acelerações lineares e velocidades angulares nos eixos _ABC, 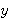_ABC e _ABC, além dos ângulos de rolamento, arfagem e guinada. Algumas medidas obtidas da IMU são pré-processadas no próprio dispositivo. Os valores de bias dos girômetros são estimados por um filtro complementar e subtraídos das velocidades angulares computadas. O filtro complementar embarcado na IMU estima também os ângulos pela combinação de girômetros e acelerômetros. Os valores dos acelerômetros indicam a aceleração instantânea a que o dispositivo está submetido e não são pré-processados. Os ângulos fornecidos pela IMU foram usados para validar o sistema de fusão sensorial e, por segurança, também para controle, uma vez que, ao contrário do que ocorre na fusão, os ângulos não dependem de o helicóptero estar no campo de visão das câmeras. O veículo carrega ainda três marcos visuais circulares coloridos. Dois deles se apoiam numa barra metálica introduzida na parte dianteira e o terceiro foi afixado na haste da cauda.

O helicóptero é observado por duas câmeras externas posicionadas a uma distância de aproximadamente 3,1 metros do solo, apontadas para baixo. A linha de base do sistema estéreo é de 24,6 cm. As câmeras são do modelo Dragonfly, fabricado pela PointGrey Research, com sensor CCD de 640x480 píxeis. As imagens coloridas são adquiridas sincronizadas via barramento IEEE1394 (Firewire) a 15 Hz. Uma visão típica das câmeras é mostrada na Figura 8. O espaço de trabalho em que o helicóptero se movimenta com segurança no campo de visão das duas câmeras é de aproximadamente 1,80 × 1,80 metros. Esse espaço é indicado com pequenas marcas no chão. Nos experimentos de controle, caso o helicóptero tenha tendência a sair do espaço de trabalho, o sistema é desligado e o helicóptero cai. Para minimizar danos por quedas e maximizar a área de trabalho, os experimentos são realizados a não mais que 30 centímetros de altura.

Uma interface microcontrolada entre o computador e o transmissor (rádio-controle) do helimodelo permite a leitura dos sinais enviados ao helicóptero. Esta leitura é importante na etapa de modelagem, quando os comandos do pilotos devem ser salvos em sincronismo com os dados de localização do helicóptero. A transmissão do sinal é feita via codificação PPM (Pulse Position Modulation), em que o valor de cada canal é representado pela largura de seu respectivo pulso. A mesma interface utilizada para ler o sinais enviados pelo piloto permite que os sinais a serem enviados ao helicóptero sejam gerados externamente. Dessa forma, a leitura dos sinais consiste em medir o valor da largura dos pulsos e a geração dos sinais é a produção de um trem de pulsos cujas larguras sejam aquelas especificadas para cada canal. Para lidar com a leitura e geração dos sinais, a interface foi construída utilizando-se um microcontrolador PIC18F2550, que, via emulação de interface RS-232 pela interface USB, se comunica com o computador, que é responsável pela localização e controle do helicóptero. O computador utilizado foi um modelo Intel Core 2 Quad, 2,4 GHz, e 2Gb de RAM com sistema operacional Windows XP.

Por ser o helicóptero Honey Bee King II um modelo de pequeno porte, com pequena capacidade de carga paga, tentou-se minimizar tanto quanto possível a quantidade de itens a bordo. Por isso, não há qualquer processamento embarcado. Todos os dados — imagens capturadas, leituras da IMU e sinais do transmissor — são transferidos via cabo para o computador para ali serem processados. No caso dos testes de controle, apenas as imagens e as informações providas pela IMU são lidas; os sinais de controle são calculados no computador e enviados ao microcontrolador, que produz então o sinal a ser enviado via rádio-controle ao helicóptero. Um diagrama com essas conexões é mostrado na Figura 9.

5.2 Sintonia do Filtro de Kalman

A sintonia do filtro foi feita de acordo com o método descrito na Seção 2.3. Inicialmente, com o helicóptero em estado estacionário — parado, mas com o motor em funcionamento —, N foi determinada pela variância das medições num intervalo de tempo de 60 segundos. N foi considerada diagonal e seus elementos foram estimados como:

Observando-se os elementos da matriz N, nota-se que o sistema de visão tem maiores dificuldades em estimar profundidade do que deslocamentos laterais. A variância associada a _D (N₃₃) é maior do que aquelas associdadas a _N e _E (N₁₁ e N₂₂, respectivamente). Além disso, N₆₆, variância das medições do ângulo de guinada, é muito menor do que as variâncias nas estimações dos outros ângulos.

Uma vez fixada a matriz de covariância do ruído de medição, foram ajustados os elementos de M, que, para simplicidade de ajuste, também foi feita diagonal. Inicialmente, fixaram-se M₁₁, M₂₂ e M₃₃ em valores bem pequenos (1,0 × 10–⁸ m²), uma vez que as equações que descrevem a evolução das posições lineares são cinemáticas e os possíveis erros associados se originam basicamente da discretização aproximada de (1). Em seguida, os demais elementos foram ajustados para que as inovações atendessem aos critérios de consistência definidos na Seção 2.3: fossem aceitavelmente brancas, de média nula e com magnitude condizente com os elementos da matriz P^yy calculada pelo filtro.

As figuras 10 e 11 mostram as propriedades estatísticas das inovações no experimento de sintonia de M. Na Figura 10, verifica-se que as inovações estão contidas num limite de três desvios padrões e têm média próxima de zero, à exceção das inovações para Φ e θ. A Figura 11 mostra que as inovações são pouco correlacionadas no tempo. No caso das inovações em Φ e θ, propositalmente, o critério de brancura das inovações bem como o critério de magnitude não foram seguidos. A razão está relacionada à estrutura física do helicóptero. A barra que sustenta os marcos visuais na parte dianteira do helicóptero ocasiona vibrações elevadas nos eixos lateral e principalmente longitudinal. Tais vibrações são percebidas como ruído de medição — as variâncias associadas a Φ e θ são maiores do que aquela associada a ψ — e também como ruído de processo, ao serem capturadas pelas medições dos girômetros e acelerômetros. Pela natureza das vibrações, é de se esperar que as variâncias de ruído de processo nas equações dos ângulos de rolamento e de arfagem, M₇₇ e M₈₈, sejam maiores do que a variância do ruído de processo na equação do ângulo de guinada, M₉₉. De fato, ao se ajustarem as variâncias dessa forma, consegue-se um maior nível de brancura das inovações, isto é, os sinais estimados usando o Filtro de Kalman tornam-se mais consistentes com os parâmetros de ruído de processo utilizados. No entanto, verificou-se na prática que os sinais medidos de Φ e θ apresentam elevadas componentes de alta frequência que não são relevantes para o problema de estabilização, e por isso preferiu-se atribuir valores menores às variâncias M₇₇ e M₈₈. Dessa forma obteve-se uma relativa atenuação das altas frequências em Φ e θ, reduzindo-se assim a variabilidade das variáveis manipuladas do sistema de controle. Ou seja, uma sintonia sub-ótima do Filtro de Kalman foi propositadamente utilizada para se obter um efeito de atenuação das altas frequências indesejadas presentes no processo de medição de Φ e θ.

Os elementos da diagonal de M após ajuste foram:

5.3 Modelagem

Um piloto experiente foi convidado a controlar e excitar o helicóptero nos experimentos de identificação. A recomendação para o piloto era manter o helicóptero em voo e ao mesmo tempo variar tanto quanto possível as entradas u, a fim de excitar em ampla faixa de frequência, todas as saídas do sistema. Dentre todos os experimentos, foram retirados dois trechos de aproximadamente 30 segundos, em que as recomendações foram de melhor forma atendidas. Um delesfoi utilizado para estimação dos parâmetros e o outro para validação do modelo.

Os parâmetros estimados pelos métodos MQ, MQP e LLA para o modelo na Equação (3) são mostrados na Tabela 1. Os métodos MQ e MQP são idênticos nos casos dos modelos de aceleração angular. Para os modelos de aceleração linear, na estimação de parâmetros por MQP, os dados são ponderados pelas estimativas das variâncias dos erros de estimação das velocidades lineares fornecidas pelo Filtro de Kalman. Observa-se que em alguns casos há grandes diferenças entre os parâmetros sugeridos por cada um dos três métodos. Na estimação de C_x há inclusive discordância sobre o sinal do parâmetro⁶. Uma das possíveis causas para a divergência entre os parâmetros é a baixa persistência de excitação dos sinais de comando produzidos pelo piloto. Contribuem ainda o pequeno tamanho da janela de dados, de cerca de apenas 30 segundos, e erros de modelo.

Para avaliar a qualidade dos modelos, calculou-se o erro de predição de um passo a frente. Apesar da sofisticação dos métodos Learn-Lagged-Acceleration e Mínimos Quadrados Ponderados, a menor diferença entre valores preditos e valores medidos foi obtida com o método de Mínimos Quadrados tradicional. As Figuras 12 e 13 mostram valores medidos e preditos num trecho de 5 segundos do experimento de validação. Parte do erro de predição pode ser explicada pelas vibrações do veículo em voo, as quais são acentuadas pela barra vertical que sustenta os marcos visuais na parte dianteira do helicóptero. Os erros de predição nas três velocidades lineares têm magnitudes próximas. Conforme mostra a Equação 1, as vibrações capturadas por girômetros e acelerômetros influem diretamente na evolução das velocidades U, V e W . No caso das velocidades angulares, os erros de predição são maiores em P do que em Q e R, uma vez que a barra, por seu posicionamento no veículo, amplifica principalmente vibrações laterais. Nota-se que o piloto trabalha conjuntamente com u_col e u_ped. De fato, uma vez que os rotores principal e de cauda são acoplados por uma correia, o comando u_col também afeta o movimento de guinada. Assim, uma parcela do erro de predição de R ocorre por se negligenciar esse acoplamento.

Apesar dos visíveis erros de predição de um passo a frente, o modelo representado pelas Equações (3) e (4) contém as relações mais importantes para o cálculo dos controladores. O modelo com os parâmetros estimados pelo método de Mínimos Quadrados foram utilizados para o projeto do sistema de controle, cujos resultados são mostrados nas próximas seções.

5.4 Sintonia dos Controladores de Altura e Atitude

No intervalo de tempo que separou a modelagem e o primeiro voo autônomo, algumas reposições de peças se fizeram necessárias, entre as quais a da bateria do helimodelo. Com a nova bateria, foi possível decolar o helicóptero com um comando υcol médio menor do que aquele utilizado para modelagem, ou seja, o ponto de operação do sistema foi alterado.

O comando u_col provoca duas ações no helicóptero: regula a velocidade do rotor principal e altera o passo de suas pás. À medida que a bateria perde capacidade de fornecer corrente, a velocidade do rotor principal diminui e, para manter altura constante, o passo das pás tem que ser aumentado. O rotor de cauda é acoplado ao principal por uma correia e, portanto, a razão das velocidades dos dois rotores é constante. O comando u_ped, responsável pelo movimento de guinada, controla o passo das pás do rotor de cauda. Com a diminuição da velocidade dos rotores, o valor médio de u_ped também é alterado.

Foram observadas também alterações no comportamento do helicóptero no decorrer de um mesmo experimento. Com o passar do tempo, à medida que a bateria perde capacidade de fornecer corrente, os pontos de operação de u_col e u_ped são alterados, como é ilustrado na Figura 14, em que o controlador deve manter a altura (_D) e o ângulo de guinada (ψ) constantes. Nesta figura e nas que se seguem no texto, as referências são mostradas em preto e os valores estimados dos estados estão em azul (linha mais clara para impressões sem cor).

Devido à substituição da bateria e pela sensibilidade das dinâmicas vertical e de guinada em relação a seu estado de carga, os controladores C_PD e C_ψ projetados com base no modelo identificado não estabilizaram p_D e ψ. Por isso, adotou-se a estratégia de ajuste empírico dos ganhos, através da qual se conseguiu um controle satisfatório dessas variáveis.

Os controladores de Φ e θ foram inicialmente sintonizados por síntese direta. Buscou-se uma resposta ao degrau criticamente amortecida com constante de tempo igual a 10 vezes o valor do período de amostragem. De acordo com o modelo, esse tipo de resposta é conseguido por um controlador PD. No entanto, controladores do tipo PD não conseguem eliminar perturbação de carga em degrau no controle dessas variáveis. Esse tipo de perturbação de fato existe, devido a acoplamentos não modelados e às incertezas na estimação dos parâmetros D₁ e D₂ do modelo (3).

Na prática, constatou-se que, devido à topologia em cascata dos controladores, o controle dos ângulos de arfagem e rolamento deve ter erro nulo. Poucos graus de desvio em relação à referência fazem com que o helicóptero saia do campo de visão das câmeras. Para neutralizar as perturbações de carga e possibilitar controle com erro nulo, foram adicionados termos integrais aos controladores de Φ e θ.

5.5 Sintonia e Rastreamento de Referências com o Controlador 1

As malhas de Φ e θ foram desconsideradas no projeto dos controladores C_x e C_y. Para que isso seja possível, as malhas de posição devem ser muito mais lentas do que as malhas internas de atitude, o que foi conseguido especificando-se uma constante de tempo de resposta ao degrau 5 vezes maior do que a da malha interna. Os ganhos foram calculados por síntese direta. Controladores PD foram utilizados. Ganhos integrais foram evitados porque o referencial {ABC} é móvel, o que implicaria somar erros em referenciais diferentes.

Para avaliar o desempenho do Controlador 1, foi realizado um experimento em que se buscou variar todas as referências das malhas externas:

_N(ref), _E(ref), _D(ref) e ψ_ref. Os eventos de variação de referência são os seguintes: degrau positivo de altura (subida); degrau em _E(ref); degrau em _N(ref); degrau em ψ_ref; degrau simultâneo em N(ref), E(ref) e ψ ref e, finalmente, degrau negativo de altura (descida). Os resultados são mostrados nas Figuras 15 a 18. Nelas, a linha tracejada vertical, no tempo t = 0, indica a transição manual-automático no controle de altura.

Apesar de as malhas internas — malhas de Φ e θ — estarem bem sintonizadas, o controle da movimentação no plano horizontal não foi satisfatório. Na ocorrência de variações na referência de p_N e p_E, ocorrem sobressinais elevados. Além disso, nos instantes em que as referências são constantes, o erro é não nulo, o que se deve à ausência de integradores nos controladores C_x e C_y.

Por volta do tempo 40 segundos, a curva de altura indica que o helicóptero possa ter caído, o que é falso. Na verdade, nesse momento, o helicóptero, devido a um sobressinal na variação de

_E(ref), sai do campo de visão das câmeras, o que faz com que o Filtro de Kalman forneça estimativas equivocadas de _D. A informação errada de altura provoca uma ação do controlador C_pD. Devido ao acoplamento dos movimentos vertical e de guinada, ocorre, nesse instante, uma perturbação em ψ. No restante do experimento, o controle do ângulo de guinada é bastante preciso e exato, inclusive na ocorrência de variações na referência.

5.6 Sintonia e Rastreamento de Referências com o Controlador 2

Os resultados da seção anterior mostram um alto nível de vibrações do helicóptero. Grande parte delas é causada pela propagação de altas frequências das malhas mais externas para as mais internas. A propagação poderia ser ainda mais agravada pela adição da malha intermediária de velocidade. Por isso, foram tomadas medidas para tornar os sinais de velocidade mais suaves.

O Filtro de Kalman originalmente proposto combina duas fontes de informação ruidosas: acelerômetros e sistema de visão estéreo. A estratégia para reduzir as altas frequências nas medições foi a substituição dos acelerômetros por um modelo de velocidade constante, isto é, nas equações de predição do filtro, as medições de aceleração são feitas iguais a zero. A falsificação dessas medições tem como consequência um atraso na estimação, pois, dessa forma, o filtro demora a perceber mudanças nas velocidades. Ressalta-se que o descarte das medidas dos acelerômetros não foi realizado devido a polarização de suas medidas, mas por capturarem frequências que, embora de fato existam no movimento do veículo, são indesejáveis no ramo de realimentação do sistema de controle. Uma estratégia que talvez conduzisse a melhores resultados seria utilizar as medições dos acelerômetros no sistema de localização e atenuar as altas frequências com pré-filtros nos controladores de velocidade e posição.

Muitos dos ajustes utilizados para o Controlador 1 puderam ser reaproveitados no projeto do Controlador 2. Os ganhos dos controladores C_pD, C_Φ, C_θ e C_ψ foram mantidos. Dessa maneira, o ajuste consistiu apenas em sintonizar os controla-dores C_U, C_V, C_x e C_y.

Os ganhos dos controladores C_U e C_V foram ajustados para que se tivesse uma resposta ao degrau criticamente amortecida 5 vezes mais lenta do que aquela das malhas internas — malhas de Φ e θ. O controlador ideal para a resposta requerida é do tipo PI. O integrador no controlador permite que sejam rejeitadas perturbações de carga constantes, que, para as malhas de velocidade, podem ser interpretadas como erro em regime permanente no controle dos ângulos. Dessa forma, poderia-se permitir um pequeno erro de controle nas malhas internas, ou seja, não seria necessária a utilização de ganhos integrais nessas malhas. Porém, como as malhas de velocidade são muito mais lentas do que as de atitude, nos testes realizados sem integrador na malha interna, o helicóptero acabou por sair do campo de visão das câmeras antes que as perturbações fossem compensadas.

Como as posições são obtidas pela integral das velocidades (desprezadando-se a rotação do helimodelo), foram utilizados controladores do tipo proporcional para C_x e C_y, que seriam suficientes para garantir erro nulo para posicionamento no plano horizontal. A malha de posição foi sintonizada para ser 5 vezes mais lenta do que a de velocidade. Mesmo fazendo-se as malhas mais externas não tão mais lentas do que as malhas internas, a constante de tempo especificada para a malha de posição é de 6,5 segundos (5 × 5 × 10 × T_s).

O experimento para avaliação do Controlador 2 tem a mesma sequência de eventos de variação de referência utilizada no experimento do Controlador 1. Os resultados são mostrados nas Figuras 19 a 22. A resposta a variações em _N(ref) e _E(ref) são bastante lentas, condizentes com a constante de tempo esperada. As oscilações nas posições horizontais foram bastante reduzidas e praticamente não há ultrapassagem na ocorrência de variação de referência. Observa-se uma redução significativa nas altas frequências, especialmente na estimação das velocidades horizontais. No entanto, em baixas frequências, as curvas de U e V oscilam consideravelmente em torno do valor de referência. Como no caso do Controlador 1, o controle de Φ e θ continua bastante preciso e exato. Dessa forma, restam as seguintes prováveis causas para as imperfeições no controle de U e V :

• para que as malhas de posição não fossem demasiadamente lentas, as constantes de tempo das malhas de velocidade foram especificadas apenas 5 vezes maiores do que as de atitude e, portanto, há um acoplamento entre as malhas;

• no modelo dinâmico adotado considera-se que U e V são afetadas unicamente por Φ e θ. É desconsiderado o fato de que, ao se inclinar, o disco de rotação das pás gera forças laterais e longitudinais, além dos torques que alteram Φ e θ;

• o descarte das informações de aceleração causa atrasos na estimação de velocidades, o que, como se sabe, reduz as margens de estabilidade.

Os resultados no controle de

_D e ψ são similares aos obtidos com a utilização do Controlador 1. Isso já era esperado, uma vez os controladores C_PDe C_ψ foram mantidos e há pouco acoplamento entre a movimentação vertical e de guinada e a movimentação horizontal.

Comparando-se os resultados experimentais do Controla-dor 1 e do Controlador 2, pode-se dizer que o segundo deixou o sistema mais estável. No entanto, o controle de velocidades não foi satisfatório, o que impede que o helimodelo possa realizar satisfatoriamente tarefas do tipo seguimento de trajetória ou seguimento de um campo vetorial. Para melhorar o controle de velocidades é necessário um estudo mais aprofundado do veículo, para que os diversos acoplamentos entre os movimentos sejam modelados e possam ser compensados com controladores mais sofisticados.

6 CONCLUSÕES

Neste trabalho, foram apresentadas e experimentadas com sucesso metodologias para localização, modelagem e controle de um helimodelo em ambientes internos. Na etapa de localização, dados de sensores inerciais foram combinados via Filtragem de Kalman a um sistema de visão estéreo para fornecer os estados necessários para as etapas de modelagem e controle. A modelagem utilizou um modelo proposto na literatura, cujos parâmetros foram estimados por métodos de identificação a partir de dados de entrada (comandos dados por um piloto) e saída (os estados fornecidos pelo sistema de localização). Os parâmetros identificados foram então utilizados para projeto de controladores PID. Resultados experimentais mostraram a estabilização de todos os graus de liberdade do helicóptero.

Diferentemente da maioria dos trabalhos encontrados na literatura, optou-se pela utilização de ambientes internos. A estratégia se mostrou eficiente na obtenção de uma prototipação rápida do sistema e proporcionou facilidades nas execuções de testes experimentais. Dessa forma, a metodologia proposta é uma alternativa interessante no estudo inicial do comportamento dinâmico de helimodelos.

Como trabalhos futuros, uma vez feita a estabilização do veículo, propõem-se testes de identificação em malha fechada, em que sinais de excitação seriam somados à saída do controlador. Outra proposta é a obtenção de modelos mais completos e a avaliação de outras estratégias de controle na plataforma de testes construída neste trabalho. Em relação à completa robotização do veículo, como mostrado na Figura 1, é ainda necessário a integração de um bloco de planejamento de movimentos. Em uma próxima etapa do projeto, deseja-se utilizar para tanto a metodologia baseada em campos vetorias proposta em (Gonçalves, Pimenta, Maia and Pereira, 2010), que já foi utilizada com sucesso para controlar quadrirrotores (Gonçalves, Pimenta, Maia, Pereira, Dutra, Michael, Fink and Kumar, 2010).

AGRADECIMENTOS

Este projeto foi financiado pela Fundação de Amparo à Pesquisa do Estado de Minas Gerais (FAPEMIG). M. A. G. Moreira agrade à CAPES pela bolsa de mestrado. G. A. S. Pereira, L. A. B. Torres e P. Iscold são bolsistas do CNPq. Os autores agradecem aos revisores do artigo, cujas sugestões o tornaram mais claro e preciso.

Artigo submetido em 28/05/2010 (Id.: 01155)

Revisado em 01/10/2010, 01/12/2010

Aceito sob recomendação do Editor Associado Prof. Marco Henrique Terra

• Abbeel, P., Ganapathi, V. and Ng, A. Y. (2006). Learning vehicular dynamics, with application to modeling helicopters, Advances in Neural Information Processing Systems (NIPS) 18
• Aguirre, L. A. (2007). Introdução à Identificação de Sistemas: Técnicas Lineares e Não-Lineares Aplicadas a Sistemas Reais, Editora UFMG, chapter 9.
• Bar-Shalom, Y., Li, X. R. and Kirubarajan, T. (2001). Estimation with Applications to Tracking and Navigation, Wiley-Interscience, chapter 5.
• Bradski, G. and Kaehler, A. (2008). Learning OpenCV - Computer Vision with the OpenCV Library, O'Reilly.
• Brandão, A., Sarcinelli-Filho, M. and Carelli, R. (2010). A nonlinear underactuated controller for 3d-trajectory tracking with a miniature helicopter, 2010 IEEE International Conference on Industrial Technology, pp. 14211426.
• Béjar, M., Ollero, A. and Cuesta, F. (2007). Modeling and control of autonomous helicopters, Advances in Control Theory and Applications, Springer Berlin / Heidelberg, pp. 129.
• Castillo-Effen, M., Castillo, C., Moreno, W. and Valavanis, K. P. (2007). Control fundamentals of small / miniature helicopters - a survey, Advances in Unmanned Aerial Vehicles, Springer Press, pp. 73118.
• Coates, A., Abbeel, P. and Ng., A. Y. (2008). Learning for control from multiple demonstrations, Proc. Int. Conf. Machine Learning, pp. 144151.
• dos Santos, F. P. (2008). Modelagem e identificação de um helicóptero em escala reduzida, Master's thesis, Universidade Federal do Rio de Janeiro.
• Gonçalves, V. M., Pimenta, L. C. A., Maia, C. A. and Pereira, G. A. S. (2010). Navegação de robôs móveis utilizando curvas implícitas, Controle & Automação 21(1): 4357.
• Gonçalves, V. M., Pimenta, L. C. A., Maia, C. A., Pereira, G. A. S., Dutra, B. C. O., Michael, N., Fink, J. and Kumar, V. (2010). Circulation of curves using vector fields: actual robot experiments in 2D and 3D workspaces, Proc. IEEE Int. Conf. Robotics and Automation, pp. 11361141.
• Gonzalez, R. C. and Woods, R. E. (2001). Digital Image Processing, Addison-Wesley Longman Publishing Co., Inc., Boston, MA, USA.
• Gyron (1998). Sistema HELIX: Histórico, perguntas mais freqüentes, descritivo técnico, especificações técnicas, aplicações, competência tecnológica, equipe, artigos publicados, parcerias., Technical report, Gyron Sistemas Autônomos.
• IARC (2010). International Aerial Robotics Competition, http://iarc.angel-strike.com
• Kalman, R. E. (1960). A new approach to linear filtering and prediction problems, Transactions of the ASME Journal of Basic Engineering 82(Series D): 3545.
• Kondak, K., Bernard, M., Meyer, N. and Hommel, G. (2007). Autonomously flying VTOL-robots: Modeling and control, Proc. IEEE Int. Conf. Robotics and Automation, pp. 736741.
• Martins, A. S., Bo, A. P. L., Borges, G. A. and Ishihara, J. Y. (2007). Design and experimental evaluation of rotor speed regulators for model helicopters in a test bench., Proc. IEEE/RSJ Int. Conf. Intelligent Robots and Systems., IEEE, pp. 16001605.
• Mettler, B., Tischler, M. B. and Kanade, T. (1999). System identification of small-size unmanned helicopter dynamics, Proc. American Helicopter Society 55th Forum
• Nonami, K. (2007). Prospect and recent research & development for civil use autonomous unmanned aircraft as uav and mav, Journal of System Design and Dynamics 1(2): 120128.
• Poynton, C. (2003). Digital Video and HDTV Algorithms and Interfaces, Morgan Kaufmann Publishers.
• Seborg, D., Edgar, T. and Mellichamp, D. (2003). Process Dynamics and Control, Wiley.
• Stevens, B. L. and Lewis, F. L. (1992). Aircraft control and Simulation, Wiley-Interscience.
• Trucco, E. and Verri, A. (1998). Introductory Techniques for 3-D Computer Vision, Prentice Hall.

1

Os símbolos

M e

N são usados para as matrizes de covariância no lugar dos tradicionais

Q e

R porque esses últimos representam velocidades angulares.

2

O símbolo

µ é utilizado para indicar as entradas do Filtro de Kalman em vez do tradicional

u para que esse último possa representar os sinais de comando do helicóptero.

3

Referencial em que o eixo

x aponta para norte (

N

orth), o eixo

y aponta para leste (

E

ast) e o eixo

z aponta para baixo (

D

own).

4

Do inglês

A

ircraft

B

ody

C

oordinate. Neste referencial, cuja origem é presa ao centro de massa do helicóptero, o eixo

x aponta para a frente, o eixo

y aponta para a direita e o eixo

z aponta para baixo.

5

Do inglês

I

nertial

M

easurement

U

nit.

6

Pela definição de

C_x na Equação (3),

C_xU é um termo de atrito viscoso e, portanto, o sinal correto de

C_x seria negativo.

Datas de Publicação

• Publicação nesta coleção
  19 Jul 2011
• Data do Fascículo
  Jun 2011

Histórico

• Aceito
  01 Dez 2010
• Revisado
  01 Out 2010
• Recebido
  28 Maio 2010