Bounds on the conical defect parameter from solar system tests

Abstract

We analyse the planetary perihelion precession and the deffection of light in the Schwarzschild field modified by a conical defect. By using observational results from solar system tests of general relativity, we obtain limits on the conical defect parameter <img src="http:/img/fbpe/bjp/v30n2/ses.gif">. For the physical case of a cosmic string the quoted limits are one and three orders weaker than the cosmological bounds.

Bounds on the conical defect parameter from solar system tests

Wilson H. C. Freire^1,2, V. B. Bezerra², and J. A. S. Lima³

¹ Universidade Regional do Cariri, Departamento de Matemática

63100-000 Crato, Ce, Brazil

² Universidade Federal da Paraíba,

Departamento de Física, Caixa Postal 5008,

58059-970 J. Pessoa, Pb, Brazil

³ Universidade Federal do Rio Grande do Norte,

Departamento de Física, Caixa Postal 1641,

59072-970 Natal, RN, Brazil

Received 25 October, 1999

We analyse the planetary perihelion precession and the deffection of light in the Schwarzschild field modified by a conical defect. By using observational results from solar system tests of general relativity, we obtain limits on the conical defect parameter

. For the physical case of a cosmic string the quoted limits are one and three orders weaker than the cosmological bounds.

I Introduction

The general theory of relativity (GTR) is believed to be the best theoretical framework presently available to describe the gravitational interaction. At the time of its formulation, the major achievements of the theory was the deflection of starlight and the perihelium shift of Mercury planet in the sun field. The remaining classical test (gravitational redshift), is really predicted by a wide range of theories since it is a direct consequence of the equivalence principle.

The bending of light and the perihelium shift agree with the Einstein values with an accurancy of one percent (an overview is given by Will [1]). Both effects are usually analysed assuming a negligible contribution from solar oblatness or whatever effect which departs the metric from exact spherical symmetry. Actually, with some few exceptions, all the calculations are done in the context of the spherically symmetric Schwarzschild metric. As a preliminary point of principle, if the Sun deviate slightly from exact spherical symmetry, either due to an appreciable solar quadrupole moment [2] or even some unexpected topological property of the gravitational field (matter distribution), a more complete treatment of such effects require a generalization of the standard Schwarzschild line element. In the case of a nonzero small quadrupole moment, the main physical consequences have been discussed with some detail in the literature either in the Newtonian approximation or in relativistic framework (see [3] and Refs. therein). However, as far as we know, an extended treatment is not only matter of academic interest, because such a possibility basically remains as an open question [1].

In the present work we are more interested on possible distortions on the Sun field provoked by topological effects. Some authors have suggested that most of simple exact solutions of Einstein's equations can easily be generalized to include a conical defect [4]. Such spacetimes are geometrically constructed by removing a wedge, that is, by requiring that the azimuthal angle around the axis runs over the range 0 < f < 2pb. For very small effects, the b parameter itself may be written as b = 1 - , where is a small dimensionless parameter quantifying the conical defect. In particular, for = 0 the Schwarzschild line element is recovered whereas for a conical defect generated by a cosmic string one has = 4Gm, where m is the mass per unit length of the string [5, 6]. We believe that it is worthwhile to consider what limits solar system observations could place on a such metric modified by the conical defect and to investigate if these observations can support the existence of a cosmic string threading the Sun.

The Schwarzschild spacetime endowed with a conical defect was considered previously [7] and some aspects were studied. The line element corresponding to this spacetime takes the following form [4]

where M = Gm is the geometric mass of the central body.

In this paper, studying the orbits of massless and massive particles in the above geometry, we derive two limits on the value of the conical defect parameter from perihelion shift of the planetary motion and deflection of light. Parenthetically, we recall that effects of nontrivial topologies are usually discussed in the cosmological framework, as for instance, in connection with the concept of small universes [8]. The physical consequences of cosmic strings regarding to its implications on the structure formation problem has also been extensively investigated [9]-[14]. More recently, the first 2-years of COBE/DMR data measuring the quadrupole anisotropies of the 3K relic radiation have been used to place limits on the possible topologies of the universe [15]. In principle, through a convenient generalization of the Friedmann-Robertson-Walker metric, a similar approach would be applied for constraining the parameter. However, it is important to derive limits on this key parameter from different kinds of phenomena, mainly in a domain where the observations envolve lenght scales diverse from that ones usually considered in the cosmological context.

Let us now consider the motion of a test particle in the Schwarzschild spacetime with a conical defect. Its trajetory can easily be established through the relativistic Hamilton-Jacobi equation

where m is the particle mass and S is the generating function.

Following standard lines, we assume an S in the form

where E is the energy and L_(b),z is the azimuthal angular momentum of the particle as measured at spatial infinity in the presence of the conical defect.

As one may check, in the spacetime given by (1) the partial Hamilton-Jacobi equation is separable and reduces to two ordinary differential equations

where K is Carter's fourth constant of motion [16], which is given by K = , with L_(b) being the total angular momentum of the particle in such background and S = r² - 2Mr. The square of L_(b) is

where p_q and p_j are the components of the generalized momentum. In particular, for a motion in equatorial plane (q = , p_q = 0) the above equation reads

and since 0 < b £ 1, we see that ³ as it should be.

The geodesic equations are easily determined by combining the above equations with the definition of the four-momentum

where s is a parameter along the trajectory. One finds

Note that the presence of the conical defect parameter through b() is the unique difference between the set (7)-(10) and the corresponding equations in the standard Schwarzschild field, which are readily recovered in the b ® 1 limit.

To analyse the influence of the conical defect on the deflection of light rays and the perihelion shift we consider the orbit equation

which is a consequence of (8) and (10), with

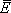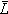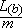_(b) and defined as _(b) = and = .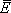

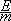Let us now proceed to limit the conical defect parameter from the perihelion shift. It is conveniente to make a change of variables u = in terms of which Eq. (11) can be recast in the following form

The standard procedure in searching for general relativistic effects in the perihelion shift is to assume a nearly circular orbit and consider the u³ term appearing in (12).

For non-circular orbits and massive particles, Eq.(12) turns into

The first term on the right-hand side of Eq.(13) leads to Newtonian orbits. If we consider only this term into Eq.(13), the approximate solution is the Newtonian solution which is given by

where j₀ and e are constants of integration, e being the eccentricity of the orbit.

Now, let us calculate the first correction by perturbation expansion. Writting u @ u₀ + u₁, where u₀ is given by Eq.(14) and considering orbits of small exccentricity we obtain the following equation for u₁(j)

whose solution is given by

Including this correction, we have that

Now, taking

the solution u(j) may be written as

From Eq.(19) we conclude that the required shift per revolution is

where 2 p(b^-1 - 1) @ 2 p is the contribution of the conical defect for the perihelion shift in the absence of local gravitational effect.

Now, expanding such expression to first order in the conical defect parameter it follows that

where Dj_S is the standard deviation in the Schwarzschild field. For the planet Mercury it is known that Dj₀ agree with Dj_S = 5 ×10^-7 to better than half percent. Expanding Eq.(20) to first order in we conclude that the conical defect parameter is bounded by

If we assume that this conical defect corresponds to a cosmic string, then its linear mass density will be bounded by

which is three orders weaker than the value predicted for grand unified strings.

Now, let us compute the total change Dj = j_+¥ - j_-¥, in the angular coordinate j of a light ray incoming from infinity with impact parameter l and escaping to infinity. From (11) we conclude that Dj is given by

In terms of the variable u previously defined, Eq.(24) becomes

where l = . Naturally, the turning point in the orbit of the light ray is also defined by

Thus, if M = 0 (only the conical defect is present) one has l = R₀ and

which is a well known result [17, 18]. Therefore, there is a deflection due to the defect even when M = 0.

When M ¹ 0 , Dj will not be equal to , as expected. As usual, to first order in M, the contribution to light deflection due exclusively to the mass M is readily obtained by inserting (26) into (24) and differentiating the resulting equation with respect to M [19]. One finds

In the limit M ® 0 and l® R₀, Eq. (28) becomes

and results in

Thus, to first order in M, the net deflection of light ( including the contributions due to the mass and to the conical defect) is given by

Naturally, as remarked before, we are looking for small deviations from Schwarzschild spacetime. Expanding (31) to first order in we obtain

where dj_S = 1.75¢¢ is the defection of light with no conical defect ( = 0). Therefore, the defect causes a deflection of size 2 p, in addition to the gravitational deflection.

Observations from photograph plates in total solar eclipses points systematically to light-deflection in the neighbourhood of the Sun. However, the experimental results are largely scattered and present noticeable discrepancies [20]. Measurements of deflection using very long baseline interferometry(VLBI) for radio waves emmited by quasars(QSO) give accuracies of about 10^-3. Therefore, using this fact and using the expansion of (31), we obtain that the conical defect parameter is bounded, in this case, by

If we assume that this conical defect corresponds to a cosmic string, this limit is of the order of magnitude of the corresponding bounds predicted by grand unified strings. This limit implies that the linear mass density of the string is such that

which is approximately of the same order of the constrain imposed by observations and by the string scenario for galaxy formation in the context of grand unified theories.

The limit that comes from the perihelion shift analysis is less precise than that one established from the deflection of light and three orders of magnitude larger than the cosmological bounds. Naturally, if some portion of the perihelion shift is due to others effects, like the quadrupole momentum of the Sun, this upper limit would be higher by the corresponding amount.

Differently from the limits on the conical parameter predicted using the observational results from the solar system tests of general relativity concerning the perihelion shift of Mercury, in the case of deflection of light the limits placed on this parameter is in good agreement with the predicted bounds for grand unified strings. Certainly, this last result does not mean that the solar system observations can support the existence of really weird matter like a cosmic string which threads the Sun. In fact, we are not addressing our questions to this point, but to the use of the observational results from the solar system in order to get bounds on the conical defect parameter which modifies the Schwarzschild metric. This approach provides, at least, an independent alternative way to get limits on the parameter that deforms the Schwarzschild solution using direct experimental test instead of cosmological considerations.

Note that from Eqs.(31) and (20), we may conclude that the conical defect induce global effects in addition to the standard deviations. Since the curvature of the Schwarzschild field with a conical defect (which can be associated with a cosmic string) does not depend on (or m), such effects are uniquely due to topological features or equivalently, due to the lack of spherical symmetry produced by the conical defect or by the cosmic string.

Finally, we stress that our results are completely general in the sense that any deviation of the b parameter from unity can be associated with other effects and not necessarily to the presence of a cosmic string.

Acknowledgments

It is a pleasure to thank Robert Brandenberger and A. R. Plastino for a critical reading of the manuscript. This work is partially supported by the the project Pronex/FINEP (No. 41.96.0908.00) and Conselho Nacional de Desenvolvimento Científico e Tecnológico-CNPq (Brazilian Research Agency).

References

[1] C. M. Will Theory and Experiment in Gravitational Physics, (Cambridge University Press, Cambridge, 1993)

[2] R. H. Dicke and H. M. Goldberg, Phys. Rev. Lett. 18, 313 (1967).

[3] I. Goldberg, Phys. Rev. Lett. 149, 1010 (1966).

[4] A. Vilenkin and E. P. S. Shellard, Cosmic Strings and other Topological Defects, Cambridge University Press (1994).

[5] A. Vilenkin, Phys. Rev D, 23, 852 (1981)

[6] J. R. Gott, ApJ 288, 422 (1985); W. A. Hiscock, Phys. Rev. D, 31, 3288 (1985).

[7] D. V. Galt'sov and E. Mazur, Teor. Mat. Fiz., 80, 288 (1989); M. G. Germano, V. B. Bezerra and E. R. Bezerra de Mello, Class. Quantum Grav., 13, 2663 (1996).

[8] G. F. R. Ellis, GRG, 2, 7, (1971); G. F. R. Ellis and G. Schreiber, Phys. Lett. A, 115, 97 (1986).

[9] A. Vilenkin, Phys. Rep., 121, 263 (1985).

[10] N. Turok and R. Brandenberger, Phys. Rev. D, 33, 2175 (1986).

[11] H. Sato, Prog. Theor. Phys., 75 , 1342 (1986).

[12] D. P. Bennett, A. Stebbins and F. R. Bouchet Ap. J 399, 5 (1992).

[13] L. Perivolaropoulos Phys. Lett. 298B, 305, (1993).

[14] V. Zanchin, J. A. S. Lima and R. Brandenberger, Phys. Rev. 54, 7129 (1996).

[15] A. de Oliveira-Costa and G. Smooth, Ap. J. 448, 447 (1995).

[16] B. Carter, Phys. Rev. 174, 1559 (1968).

[17] P. de Sousa Gerbert and R. Jackiw, Comm. Math. Phys. 124, 229 (1989).

[18] D. V. Gal'tsov and E. Masar, Class. Quantum Grav. 6 1313 (1989).

[19] R. Wald, General Relativity, University of Chicago Press, 1984.

[20] H. von Klubber, "The Determination of Einstein's Light-deflection in the Gravitational Field of the Sun" in Vistas in Astronomy Vol. 3, Pergamon Press, pp. 47 (1960).

Publication Dates

• Publication in this collection
  07 Jan 2002
• Date of issue
  June 2000

History

• Received
  25 Oct 1999