Classification of basis states for (p-f)-nuclei (41 <= A <= 80) with minimal configuration energy

Classification of basis states for (p–f)–nuclei (41 £ A £ 80) with minimal configuration energy

J.A. Castilho Alcarás^I; J. Tambergs T. Krasta J. Rua^II; O. Katkeviius^III;

^IInstituto de Física Teórica, UNESP, 01405-900, São Paulo, Brazil

IIRadiation Physics Laboratory, Institute of Solid State Physics, University of Latvia, Salaspils, Latvia

IIIInstitute of Theoretical Physics and Astronomy, 2600 Vilnius, Lithuania

^{Address to correspondence}

ABSTRACT

We give a complete classification of basis with unitari (U(A–1), U(3)) and permutational (S)A)) symmetries. Thse are suitable as functions for (p–f)– nuclei (41£ A £ 80) with minimal configuration energy. We also give a brief survey of way in which are obtained.

1 Introduction

In the tradicional nonrelativistic treatment, the nucleus is considered as a system of A fermions, the nucleons, with spin and isospin 1/2, and three spatial degrees of freedom interacting through one– and two–body forces. The bound states of such a system are described by totally antisymmetric wave functions.

The introduction of Jacobi vectors

allows us to remove the center of mass and pay attention only to the relative motion described by the translationally invariant Jacoby vectors

₁,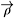₂,...,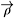_{A-1 .}

To describe the bound states of such system, we will use as basis the basis functions of irrep [1^7(A-1)] of U(7(A-1)) É U^(r)(3(A-1))×U^(s)(4(A-1)). The spin-isospin part is described using the chain

while the space part is described by

The labelling of basis functions in the spin-isospin chain of subgroups, Eq.(3), is given by the Wigner Supermultiplet Theory.

We will focus our attention on the problem of labelling the basis functions for the space chain of subgroups, Eq(4).

Since the basis functions of irrep {} of U(3(A-1)) are functions only of the coordinates of the first A-1 Jacobi vectors, they have to be symmetric. We then write {} = {E}. Since the wave functions of the p-dimensional harmonic oscillator carry the irrep {E} of U(p), it is usual to associate E with the configuration energy of the nuclear states whose space part is described by wave functions labelled by the chain (4).

This association allows us to stablish a link with the harmonic oscillator shell model. The basis functions of the irrep {E} could alternatively be labelled by the chain of subgroups

in which each link U⁽ⁱ⁾(3) acts only in the 3 coordinates of the Jacoby vector 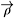_i. In this case the irreps associated to these U⁽ⁱ⁾(3) would be all symmetric [E⁽ⁱ⁾] and their basis functions would be eigenstates of harmonic oscillators with energy ⁽ⁱ⁾ = (E⁽ⁱ⁾+3/2)w and it would result

The number of linearly independent wave functions of the 3-dimensional harmonic oscillator with energy = (E+3/2)w is equal to the dimension of the irrep {E} of U(3) given by

In this way, by the Pauli principle, in the E shell one can put at most 4dim_{E} = 2(E+1)(E+2) nucleons. The minimal configuration energy is obtained by filling the shells E = 0(s),E = 1(p),E = 2(s-d),...,E₀–1 and putting the remaining nucleons in the first partially filled shell E₀. In this way, it follows that

where n₀ is the number of nucleons in the partially filled shell E₀.

Our aim is to label the states of a system of A nucleons with minimal configuration energy with the labels given by the unitary chain (4).

In [1], Elliott gives the labelling for p– and (s–d)–nuclei in a different, but equivalent, organization than the one used here. In his paper, Elliott only mentions that the classification was obtained by the plethysm technique.

In a recent paper [2], which we will refer to as (I), we review the plethysm technique, propose a general algorithm to compute all plethysms of two Schur functions of degrees n and m using as input the plethysm {n} Ä{m} of symmetric Schur functions [3] and show how the plethysm technique can be applied to our problem. Ultimately, one has to find the reduction U(A-1) É O(A–1) É S(A). [We refer the readers to (I) for definitions and notations.] An alternative method for obtaining the reduction O(A–1) É S(A), exploiting the complementarity between O(A–1) and Sp(3,R) was proposed in [7].

According to the plethysm technique exposed in (I), the groups U(3) and U^(r)(A–1) in Eq.(4) must share the same irrep

and the irreps [] of S^(r)(A) and S^(s)(A) must be conjugate to each other.

The branching rules for irreps in the restriction U(n) ® O(n) have definite rules [4,5,6,2]. According to them, for states of minimal configuration energy, the irrep of O(n) in this restriction is the same as the one of U(n). This then fixes the O(A–1) irrep. Then we must concern ourselves only with the restriction U^(r)(A–1) É S(A)^(r).

Besides, the Pauli principle imposes an additional restriction. The treatment of the spin-isospin part by the Wigner supermultiplet model implies that the S^(r)(A) irrep [] must have at most 4 lines, that is,

Therefore {}, being its conjugate, must have at most 4 columns.

2 Reduction U(A-1) É S(A)

The reduction U(A–1) É S(A) is given by the inner plethysm {A–1,1} {¢} of U(A-1) irreps expanded in terms of S(A) irreps

where V¢¢¢ are numerical coefficients, {} are U(A–1) irreps and r¢¢ = å are their degrees.

The numerical coefficients and the U(A–1) irreps are obtained by the following procedure.

One first defines the operator ({}) by its action on an U(A–1) irrep {m}:

where a({}{m} ® {m¢}) is the multiplicity of irrep {m¢} in the outer product {}{m}.

From the properties of the outer product of Schur functions, it follows that the operators satisfy the relations:

Next one defines an operator by

where {j₂},{j₃},... are symmetric Schur functions and the {}_t2,{}_t3,... are general Schur functions of degrees t₂,t₃,... . [ Note that the only plethysms needed are those with a symmetric Schur function in the left. An algorithm to compute them is presented in (I).]

The action of over an U(A-1) irrep {¢} , by use of (13) and (14) is transformed in a sum of irreps {¢¢} with multiplicities V¢¢¢:

This expression provides the numerical coefficients V¢¢¢ and the U(A–1) irreps {¢¢} that appear in (11). To each U(A–1) irrep {¢¢} corresponds one S(A) irrep [] = [].

This is the mathematical framework. When applied to the classification of nuclear states new ingredients appear. First, the U(A–1) irrep {¢} in which acts has, by (9), at most 3 rows. Second, the S(A) irreps [] = [A-r¢¢,] with physical meaning, by (10), are only the ones with at most 4 columns, that is,

The k_i are interpreted[8] as the number of space levels occupyied by 1,1,3,4 nucleons, respectively.

These conditions restrict the t_k and j_k in (15) that may give meaningful S(A) irreps [] when is applied to a given U(A–1) irrep {¢} representing a nuclear state with configuration energy E ³ E_min . These t_k and j_k are obtained following 2 steps:

1) take a nonnegative integer i in the range

2) for each i in this range, find the nonnegative integers j_k and t_k that satisfy

where r¢¢ must be in the range

Once these t_k 's and j_k 's are obtained, one replaces them in (15) applied to {¢}, computes the resulting plethysms and outer products, linearizes the resulting expression with respect to using (13) and (14) ending with an expression of type (16). From the S(A) irreps [] = [A-r¢¢,] produced by each {¢¢} one keeps only the ones that satisfy (17).

For E = E_min, which we are interested in, the solutionis of steps 1) and 2) for nuclei with A £ 80 are given below.

For p-nuclei (5 £ A £ 16), E_min = A–4,

and the reduction U(A–1) É S(A) is

[here and in the following the symbol means that on the RHS only the terms which may produce physically acceptable S(A) irreps are considered.]

For (s–d)–nuclei (17 £ A £ 40), E_min = 2A-20 ,

[The symbol denotes a reduced plethysm, that is, a plethysm expansion in which only the terms with up to 3 rows are considered.]

The Schur function {4³,{}_A–16} will produce, by Eq.(11), S(A) irreps [4⁴,{}_A–16].

For (p–f)–nuclei (41 £ A £ 80), E_min = 3A–60,

The Schur functions {4⁹,{}_A–40} will produce, by Eq.(11), S(A) irreps [4¹⁰,{}_A–40].

Analogous to the case of p– and (s–d)–nuclei, Eq.(26) allows us to read the reduction U(A–1) É S(A) for nuclei in the ground configuration of this shell directly from the table of multiplicities of Schur functions {}_3(A–40) in the reduced plethysms {3} {}_A–40. The column associated to a given Schur function {}_3(A–40) corresponds to the U(A–1) irrep {20³}+{}_3(A–40) . Its entries, in each line labelled by {}_A–40 give the multiplicity of S(A) irrep [4¹⁰,{}_A–40] in the reduction.

The U(A–1) É S(A) reductions for p– and (s–d)– nuclei in minimal energy configuration are given in (I) and in [1] in a different organization.

For (p–f)–nuclei the reductions are given in the tables below.

3 Explanation of tables

The equations in the tables give the reduction of U(A–1) irrep {E₁,E₂,E₃} into S(A) irreps []. On their RHS are listed only the S(A) irreps physically acceptable, that is, those satisfying (17) as the symbolindicates.

For a given A and minimal configuration energy, only the U(A–1) irreps that have at least one physically acceptable irrep in its reduction to S(A) are listed.

Only the first half of the shell (41 £ A £ 60) is listed in the tables. The second half, (61 £ A £ 79), is obtained by the use of particle-hole symmetry in the open shell. For this shell this symmetry reads as

For A = 80 one has

In the tables are listed only the first 5 irreps {E₁,E₂,E₃} more symmetric in U(3) labels, i.e., those with greatest values of U(3) Casimir invariant.

TABLES

O. Katkeviius

Institute of Theoretical Physics and Astronomy, 2600 Vilnius, Lithuania

Received on 15 March, 2002

• [1]J. P. Elliott, Proc. Roy. Soc. A245, 128 (1958).
• [2]J. A. Castilho Alcarás, J. Tambergs, T. Krasta, J. Ruza J. Ruza, and O. Katkevicius,  Braz. J. Phys. 32, 641 (2002).
• [3]O. Egecioglu and J. B. Remmel, Atomic Data and Nuclear Data Tables, 32, 157 (1985).
• [4]D. E. Littlewood, The Theory of Group Characters (Oxford Univ. Press, Oxford, 1958).
• [5]B. G. Wybourne, Symmetry Principles and Atomic Spectroscopy (Wiley, New York, 1970).
• [6]V. Vanagas, Algebraic Methods in Nuclear Theory, in Russian (Mints, Vilnius(Lithuania), 1971).
• [7]M. J. Carvalho, J. Phys. A23, 1909 (1990); Comp. Phys. Comm. 96, 288 (1996).
• [8]J. M. Blatt and V. F. Weisskopf, Theoretical Nuclear Physics (John Wiley, New York, 1960).

Address to corresponce

J.A. Castilho Alcarás

Instituto de Física Teórica, UNESP,

01405-900, São Paulo, Brazil

Publication Dates

• Publication in this collection
  23 Apr 2003
• Date of issue
  Mar 2003

History

• Received
  15 Mar 2002