Geometrical generation of cosmic magnetic fields within standard electromagnetism

Abstract

We study the evolution of cosmological magnetic fields in FRW models with curved spatial sections and outline a geometrical mechanism for their superadiabatic amplification on large scales. The mechanism operates within standard electromagnetic theory and applies to FRW universes with open spatial sections. We discuss the general relativistic nature of the effect and show how it modifies the adiabatic magnetic evolution by reducing the depletion rate of the field. Assuming a universe that is only marginally open today (i.e. for 1-omega0 ~ 10-2), we estimate the main features of the superadiabatically amplified residual field and find that is of astrophysical interest.

Geometrical generation of cosmic magnetic fields within standard electromagnetism

Christos G. Tsagas^{I, II}; Alejandra Kandus^III

^IDAMTP, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK

^IIDepartment of Physics, Aristotle University of Thessaloniki, Thessaloniki 54124, Greece

^IIILATO-DCET, Universidade Estadual de Santa Cruz, Rodovia Ilhéus-Itabuna km 16 s/n Salobrinho CEP-05508-900, Ilhéus - BA, Brazil

ABSTRACT

We study the evolution of cosmological magnetic fields in FRW models with curved spatial sections and outline a geometrical mechanism for their superadiabatic amplification on large scales. The mechanism operates within standard electromagnetic theory and applies to FRW universes with open spatial sections. We discuss the general relativistic nature of the effect and show how it modifies the adiabatic magnetic evolution by reducing the depletion rate of the field. Assuming a universe that is only marginally open today (i.e. for 1-W₀ ~ 10^-2), we estimate the main features of the superadiabatically amplified residual field and find that is of astrophysical interest.

I. INTRODUCTION

Magnetic fields appear everywhere in the universe [1]. Despite this and the numerous scenarios of magnetogenesis the origin of cosmic magnetism remains a mystery [2]. These scenarios are generally classified into those arguing for a late (post-recombination) magnetic generation and those advocating a primordial origin for the fields. Early magnetogenesis is attractive because it makes the ubiquity of large-scale magnetic fields in the universe easier to explain. Inflation seems the plausible candidate for producing the primordial fields, as it naturally leads to large-scale phenomena from subhorizon microphysics. The main obstacle is that any magnetic field that survives inflation is so drastically diluted that it can never seed the galactic dynamo. The reason is the 'adiabatic', a^-2 decay of the field (a is the scale factor of the universe). This is attributed the to conformal invariance of standard electromagnetism and to the conformal flatness of the Friedmann-Robertson-Waler (FRW) models. Strictly speaking, however, this is only true in FRW spacetimes with flat spatial sections.

The usual way of modifying the B µ a^-2 law is by breaking away from standard electromagnetic theory. Turner and Widrow did this by introducing to their Lagrangian an extra coupling between the Maxwell field and the curvature of the spatially flat FRW spacetime [3]. The conformal invariance and the gauge invariance of Maxwell's equations were lost as a result, but a new magneto-curvature term appeared in the magnetic wave equation. The immediate consequence was a superadiabatic-type amplification of the primordial field. To be precise, superhorizon-sized magnetic fields, evolving in a poorly conducting inflationary universe, decayed as a^-1 [3]. Since then, many scenarios of early magnetic amplification have appeared in the literature (e.g. see [4]).

Here we discuss a conventional interaction between the electromagnetic and the gravitational field, which so far has been sparsely studied in cosmology. This is the natural, general relativistic coupling between electromagnetism and space-time geometry that emerges from the vector nature of the Maxwell field and from the geometrical approach of Einstein's theory (e.g. see [5, 6]). Our mechanism operates primarily on magnetic fields coherent on the largest subcurvature scales of a spatially open FRW universe, which asymptotically approaches flatness as it undergoes a period of inflationary expansion. The result is that these fields decay as a^-1, a rate considerably slower than the adiabatic a^-2 law. Then, assuming that 1-W ~ 10^-2 today, we find that a residual field of approximately 10^-35 G on a comoving length of ~ 10⁴ Mpc [6]. This is much stronger than any other large-scale field obtained by conventional methods. Moreover, in a dark-energy dominated universe, seeds field of 10^-35 G lie within the broad galactic dynamo requirements [7].

II. SUPERADIABATIC MAGNETIC AMPLIFICATION IN FRWUNIVERSES

Consider a large-scale magnetic field B_a and introduce the rescaled magnetic fux variable _a = a²B_a. Also, adopt the decomposition _a = _(n), with being the standard vector harmonics, and use conformal instead of proper time. The wave-equation of the field, linearised around a FRW background with curved spatial sections, reads [5, 6]

Here n is the comoving wavenumber of the mode, k = 0,±1 is the curvature index of the background 3-space and a prime indicates conformal time derivatives (see [5, 6] for details). The above closely resembles Eq. (2.15) in [3]. The similarity is in the presence of a curvature related source term in both expressions. The difference is that here the magneto-curvature term is a natural general relativistic effect. No new physics has been introduced and standard electromagnetism still holds. For k = 0 Eq. (1) reduces to the well known Minkowski-space expression, which leads to the adiabatic B_a µ a^-2 decay for the field. When k = +1 the compactness of the space guarantees that B_a still drops as a^-2 despite the presence of the magneto-curvature term [6]. However, for k = -1 and on the largest subcurvature scales we obtain

with

₁ and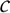 ₂ constants [6]. Thus, in a spatially open FRW universe and near the curvature scale the dominant magnetic mode never depletes faster than a^-1. This means an effective superadiabatic amplification of the field due to curvature effects alone (see [6] for details). Note that at the onset of inflation subcurvature scales are in causal contact if the universe is sufficiently open (e.g. W < 0.1 will suffice). On wavelengths larger than the curvature scale the depletion rate of the field is even slower. As n®0, for example, we find that B_a µ 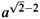. It should be noted, however, that these supercurvature scales lie always outside the horizon.

III. THE AMPLIFIED RESIDUAL FIELD

Following [3], the energy density of the n-th magnetic mode as it crosses outside the horizon is r_B = (M/m_Pl)⁴r, where r ~ M⁴ is the total energy density of the universe and m_Pl is the Planck mass. When B_a µ a^-2 we have [3]

at the end of inflation. Note that r_g is the radiation energy density and is the comoving scale of the field (in Mpcs and normalized so that is the physical scale today). The situation changes if during inflation the field decays as a^-1 instead of following the adiabatic a^-2-law. For a direct comparison, it helps to follow the analysis of [3]. Consider a typical GUT-scale inflationary scenario with M ~ 10¹⁷ GeV and reheating temperature T_RH ~ 10⁹ GeV. Then, for B_a µ a^-2, the energy density stored in a given magnetic mode at the end of inflation is [6]

instead of (3). After inflation the high conductivity of the plasma is restored. This ensures that B µ a^-2 and consequently that the ratio r = r_B/r_g ~ 10^-51 remains fixed. If 1-W₀ is of the order of 10^-2, as it appears to be today [8], the current curvature length is (l_k)₀ = (l_H)₀/ ~ 10⁴ Mpc (see [6] for further details). By substituting this scale into expression (4) we find that r = r_B/r_g ~ 10^-59, which corresponds to a magnetic field with current strength around 10^-35 G. The latter is within the lower values required for large scale galactic dynamo to operate in a dark-energy dominated universe [7].

IV. DISCUSSION

Although all three of the FRW spacetimes are conformally flat they are clearly not the same. Their different geometries are manifested by the fact that, while for k = 0 the conformal factor is the cosmological scale factor, in the other two cases it is not. Thus, the conformal flatness of the Friedmann models does not a priori guarantee the adiabatic B_a µ a^-2-law in all FRW universes. By allowing for curved spatial sections, we showed the presence of an extra curvature-related source term in the magnetic wave equation. When k = -1, this meant that large-scale fields evolving through a period of inflationary expansion decay as a^-1 instead of a^-2. As a result, primordial magnetic fields coherent on the largest subcurvature scales could survive an epoch of inflation and still be strong enough to sustain the dynamo process.

If the universe is marginally open today, our mechanism allows for a simple, viable and rather efficient amplification of large-scale primordial magnetic fields to strengths that can seed the galactic dynamo. Even if the universe is not open, however, this study still provides a clear counter example to the widespread perception that the superadiabatic magnetic amplification on FRW backgrounds is impossible unless standard electromagnetism is violated.

Acknowledgements

We would like to thank Anthony Challinor, Anne Davis, Carlos Martins, Kandu Subramanian, Shinji Tsujikava and Larry Widrow for helpful discussions and comments. A. Kandus acknowledges FAPESB (Fundação de Amparo a Pesquisa do Estado da Bahia) for financial support to attend the conference.

References

[1] P.P. Kronberg, Rep. Prog. Phys. 57, 325 (1994); R. Beck, A. Brandeburg, D. Moss, A.A. Sukurov and D. Sokofoll, Annu. Rev. Astron. Astrophys. 34, 155 (1996); J.-L. Han and R. Wielebinski, Chin. J. Astron. Astrophys. 2, 293 (2002)

[2] K. Enqvist, Int. J. Mod. Phys. D 7, 331 (1998); D. Grasso and H. Rubinstein, Phys. Rep. 348, 163 (2001); L.M. Widrow, Rev. Mod. Phys. 74, 775 (2002); M. Giovannini, Int. J. Mod. Phys. D 13, 391 (2004)

[3] M.S. Turner and L. Widrow, Phys. Rev. D 37, 2743 (1988).

[4] B. Ratra, Astrophys. J. Lett. 391, L1 (1992); A.D. Dolgov, Phys. Rev. D 48, 2499 (1993); E.A. Calzetta, A. Kandus and F.D. Mazzitelli, Phys. Rev. D 57, 7139 (1998); O. Bertolami and D.F. Mota, Phys. Lett. B 455, 96 (1999); A.C. Davis, K. Dimopoulos, T. Prokopec and O. Törnkvist, Phys. Lett. B 501, 165 (2001)

[5] C.G. Tsagas, Class. Quantum Grav. 22, 393 (2005)

[6] C.G. Tsagas and A. Kandus, Phys. Rev. D 71, 123506 (2005).

[7] A.-C. Davis, M. Lilley and O. Törnkvist, Phys. Rev. D 60, 021301 (1999)

[8] M. Tegmark et al. (the SSDS collaboration), Phys. Rev. D 69, 103501 (2004).

(Received on 27 September, 2005)

Publication Dates

• Publication in this collection
  18 Jan 2006
• Date of issue
  Dec 2005

History

• Received
  27 Sept 2005