Square-gradient scattering mechanism in surface-corrugated waveguides

Abstract

In this work we study the surface scattering mechanisms from rough surfaces of a multimode quasi-1D waveguide (conducting quantum wires). The square-gradient scattering mechanism, which was missed in existing studies of the transport through surface-corrugated waveguides, is discovered. The main attention is paid to the interplay between the new mechanism and the known one, as well as its effect on the waveguide transport properties. For any value of the roughness height sigma, the square-gradient terms in the expression for the wave-scattering length (electron mean-free path) are dominant, provided the correlation length Rc of the surface disorder is small enough.

Surface scattering; Wave propagation in random guiding media; Electronic transport in quantum wires

SURFACES, INTERFACES, AND THIN FILMS

Square-gradient scattering mechanism in surface-corrugated waveguides

F. M. Izrailev^I; N. M. Makarov^II; M. Rendón^III

^IInstituto de Física, Universidad Autónoma de Puebla, Puebla, Pue., 72570, Mexico

^IIInstituto de Ciencias, Universidad Autónoma de Puebla, Puebla, Pue., 72050, Mexico

^IIIFacultad de Ciencias de la Electrónica, Universidad Autónoma de Puebla, Puebla, Pue., 72570, Mexico

ABSTRACT

In this work we study the surface scattering mechanisms from rough surfaces of a multimode quasi-1D waveguide (conducting quantum wires). The square-gradient scattering mechanism, which was missed in existing studies of the transport through surface-corrugated waveguides, is discovered. The main attention is paid to the interplay between the new mechanism and the known one, as well as its effect on the waveguide transport properties. For any value of the roughness height s, the square-gradient terms in the expression for the wave-scattering length (electron mean-free path) are dominant, provided the correlation length R_c of the surface disorder is small enough.

Keywords: Surface scattering; Wave propagation in random guiding media; Electronic transport in quantum wires

The wave transport through guiding surface-disordered systems is an important topic with many applications in the physics of waveguides and mesoscopic devices for which the roughness of boundaries is due to either inevitable imperfections or artificial patterns (see, e.g., Refs. 1-8 and references therein). The goal of this contribution is to study the different mechanisms of surface scattering in multimode quasi-1D waveguides with rough surfaces. In order to treat the rough-surface-scattering problem, we transform it to a bulk one that is described by an effective Hamiltonian with a scattering potential Û and flat boundaries. It is important to point out that the potential Û has a specific structure whose detailed analysis gives rise to discover an unexpected scattering mechanism, which prevails in the commonly used region of small-scale boundary perturbations.

In what follows, we consider an open plane waveguide (or conducting quasi-one-dimensional quantum wire) of average width d, stretched along the x-axis. For simplicity, one (lower) surface of the waveguide is assumed to be flat, z = 0, while the other (upper) surface has a rough profile, z = d + sx(x); with s as the root-mean-square roughness height. The fluctuating wire width w(x) is defined by

The random function x(x) describes the roughness of the upper boundary. It has unit root-mean-square value and is assumed to be a statistically homogeneous and isotropic Gaussian random process with zero average,

Here the angular brackets stand for statistical averaging over different realizations of the surface profile x(x). We also assume that its binary correlator (x) decreases on the scale R_c and has the normalization (0) = 1; the correlation length, R_c, is the measure of the profile roughness. The roughness-height power (RHP) spectrum W(k_x) is defined by

Since (x) is an even function of x, its Fourier transform (3) is even, real and nonnegative function of k_x. The RHP spectrum, W(k_x), has maximum at k_x = 0 with W(0) ~ R_c, and decreases on the scale .

In order to analyze the rough surface scattering for our model, we employ the method of the retarded Green's function (x,x';z,z'). Specifically, we start with the Dirichlet boundary-value problem

Here the wave number k is equal to w/c for an electromagnetic wave of the frequency w and TE polarization, propagating through a waveguide with perfectly conducting walls. As for an electron quantum wire, k is the Fermi wave number within the isotropic Fermi-liquid model. In order to express the rough surface scattering as a bulk one, we perform the transformation to new coordinates,

in which both surfaces of the waveguide are flat. Correspondingly, we introduce the canonically conjugate Green's function,

_new = d^-1

_old and omit the subscript "new" in what follows. As a result, we arrive at an equivalent Dirichlet boundary-value problem, i.e., the new problem fulfills the conditions

At the same time, we obtain an effective surface scattering potential given by

Note that the prime over the function x(x) denotes derivative with respect to x.

With the help of the Green's theorem, the problem can be reformulated as the following Dyson-type integral equation

The Eq. (8) relates the perturbed by surface disorder Green's function (x,x';z,z') to the Green's function ₀(|x - x'|;z,z') of the waveguide with flat boundaries and zero bulk potential.

In the expression (7), which is exact and valid for any form of w(x), one can distinguish three different scattering terms. The first one depends only on the rough profile, x(x), through the fluctuating wire width i(x) (see Eq.(1)). The second and third terms are related to the profile's derivative, x'(x), and the square of the profile's derivative, x'²(x), respectively. In this connection one should distinguish between the amplitude, gradient and square-gradient scattering (SGS) mechanisms. In the exact expression for Û(x,z) the contribution of these mechanisms emerges in a mixed way, but with a detailed analysis we have found a way to separate them and then we arrive at a very useful approximate expression with three groups of terms, each of them associated with the above scattering mechanisms. The first and second groups, related respectively to the mechanisms of amplitude and gradient scattering, are controlled by the parameter s/d. The third group, which is due to the square-gradient mechanism, is controlled by (s/d)². Since the last mechanism seems to be much weaker in comparison with the others (in the case of small surface corrugations, s d), it was neglected in previous analytical studies of rough surface scattering performed with an approximation in the lowest order in s. We discover, however, that apart from the (s/d)²-dependence of this mechanism, the independent parameter R_c, also has control over it.

The square gradient terms introduce the zero-mean-valued operator (x) = x'²(x) - áx'²(x)ñ, which plays a special role. Its binary correlator,

determines the square-gradient power (SGP) spectrum

One should stress that although by integration by parts the power spectrum of the roughness gradients sx'(x) can be reduced to the RHP spectrum W(k_x), this is not possible for the SGP spectrum T(k_x). This very fact reflects a highly non-trivial role of the square-gradient scattering, giving rise to the competition with the well known amplitude scattering, in spite of the seeming smallness of the term s²x'²(x).

To proceed, we pass from the problem for the random Green's function, (x,x';z,z'), in Eq.(8), to the problem for the Green's function á(x,x';z,z')ñ averaged over the surface disorder. To perform the averaging we can apply one of the standard and well known perturbative methods. For example, it can be the diagrammatic approach [10] or the technique developed in Ref. 2. Both of the methods allows one to develop the consistent perturbative approach, with respect to the scattering potential, which takes adequately into account the multiple scattering from the corrugated boundary. After quite cumbersome calculations, where the proper self-energy in the Dyson-type equation was obtained within the second-order approximation in the perturbation potential, we obtain the desired average Green's function. This function, in the normal-mode representation, has the form

Here k_n = corresponds to the unperturbed lengthwise wave number k_x, and N_d = [kd/p] is the number of propagating modes (or conducting electron channels) determined by the integer part [...] of the ratio kd/p.

Our interest is in the attenuation length or total mean free path L_n of the n-th mode. Its inverse value is given by the imaginary part of the proper self-energy and, in accordance with the form of the scattering potential, consists of two terms describing different scattering mechanisms,

The first length 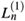is determined by the expression

Here the term corresponding to n' = n is related to the amplitude scattering while the terms with n' ¹ n result from the gradient one. Eq. (13) coincides with that previously obtained by different methods (see, e.g., Ref. 1).

The SGS length 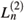is associated solely with the square-gradient mechanism due to the operator (x),

Its term with n' = n describes the intramode scattering,

The partial lengths specify the intermode scattering (from n to n' ¹ n channel),

To the best of our knowledge, in the surface-scattering problem for multi-mode waveguides the operator (x) was never taken into account, and, as a result, the square-gradient attenuation length 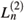was missed in previous studies.

A detailed analysis of the requirements under which Eqs. (12) - (16) are derived give us the following conditions of weak scattering [9]:

Here L_n is the distance between two successive reflections of a wave from the rough surface inside the nth channel. The conditions (17) imply that the wave is weakly attenuated on both the correlation length R_c and the cycle length L_n. Note that they implicitly includes the requirement that the surface corrugations are small in height (s d), but does not restrict the value s/R_c of the roughness slope.

Hereafter we confine ourselves to the analysis of the widely used case of small-scale boundary perturbations, when kR_c 1. In this case the surface roughness can be regarded as a delta-correlated random process with the correlator (x - x') » W(0)d(x - x') and a constant power spectrum W(k_x) » W(0) ~ R_c. Taking into account the evident relationship kL_n 1, one can get the following inequalities to specify this case

It is necessary to underline that in the regime of small-scale roughness (18) the second of the weak-scattering conditions (17) is not so restrictive as the first one and directly follows from it, R_c L_n 2L_n.

Under the conditions (18), in Eqs. (13), (15) and (16) for the attenuation lengths, the argument of the correlators W(k_x) and T(k_x) turns out to be much less than the scale of their decrease . Therefore, for any item of the sum over n', the argument can be taken as zero.

The first attenuation length is presented by

Due the large number of the conducting modes N_d » kd/p 1, we can change the sum over n' to an integral. In this way we obtain Eq. (19b) from Eq. (19a). In order to correctly estimate the result, one can take into account the formula

which directly follows from the definition (3) for the Fourier transform W(k_x) of the binary correlator (x). The function (R_cr) is the dimensionless correlator of the dimensionless variable r with the scale of decrease of the order of one. So, the function (R_cr) does not depend on R_c. Therefore, the integral over r entering Eq. (20) is a positive constant of the order of unity. For example, W(0) = R_c and the integral is in the case of Gaussian correlations.

For the SGS length in Eq. (14), we have a fast decay of the terms under the sign of sum, with the increase of the absolute value of Dn = n - n'. This can be seen by making use of the following estimate,

If for simplicity we take the case N_d n 1, the sum can be well evaluated just by its three terms with n' = n, n ± 1. Thus, we obtain

The explicit form for T(0) directly follows from the definition (10) for the correlator T(k_x),

If the roughness correlations are Gaussian, we have T(0) = 3/4 and the integral over r entering Eq. (23) is equal to 3/4.

As follows from Eq. (13), with the decrease of kR_c the inverse value of the first attenuation length typically decreases. In contrast, from Eq. (14) one can see the monotonous increase of the inverse SGS length with the decrease of kR_c. Specifically, we have 1/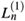µ kR_c and 1/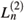µ (kR_c)^-3.

According to this analysis it becomes clear that the curves displaying 1/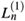 and 1/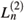, with respect to kR_c, must intersect, and one can observe the crossover from the square-gradient to amplitude surface scattering. If the crossing point, (kR_c)_cr, falls onto the present region of small-scale roughness (kR_c 1), its dependence on the model parameters can be estimated by equating to one the ratio of the asymptotics (19b) and (22). Thus, we have

To the left from this point (kR_c)_cr the SGS length prevails,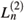

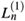. To its right the main contribution is due to the first attenuation length,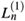

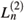. The expression (24) shows that the crossing point is smaller for smaller values of the dimensionless roughness height ks, as well as for smaller mode indices n, or for larger values of the parameter kd/p. This analytical estimation determine the region of small values of R_c, where the new attenuation length 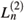should not be neglected, in spite of the fact that 1/ 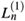is proportional to s² while 1/ 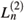is proportional to s⁴.

In Fig. 1 we display separately the behavior of L_n/2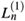 and L_n/2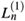, as a function of the dimensionless correlation parameter kR_c. With dashed lines we plot the asymptotics (19b) and (22) for the region (18). One can make sure that within this region both lengths are sufficiently well described by their corresponding asymptotic expressions.

The figure also shows the crossing point between L_n/2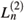 and L_n/2 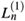for two values of (ks)² and mode index n. This point for the couple of curves with parameters (ks)² = 10^-4 and n = 50, is very close to that for the couple with parameters (ks)² = 10^-2 and n = 10. Approximately, both points are (kR_c)_cr ~ 0.2. They are well located in the interval of small-scale roughness and their values are in agreement with (24). The couple of curves corresponding to the parameters (ks)² = 10^-2 and n = 50, has a crossing point in the transition region kR_c ~ 1 between small- and large-scale corrugations.

In conclusion, we have discovered the square-gradient scattering mechanism which was missed in existing studies of the transport through surface-corrugated waveguides. In characterizing its contribution we have found that it prevails in the region of small-scale perturbation, kR_c 1, where the surface roughness is typically described by a white-noise potential.

Acknowledgments

This research was partially supported by the CONACYT (México) grant No 43730, and by the VIEP-BUAP (México) under the grant 5/G/ING/05.

[1] F. G. Bass, I. M. Fuks, Wave Scattering from Statistically Rough Surfaces (Pergamon, New York, 1979).

[2] A. R. McGurn and A. A. Maradudin, Phys. Rev. B. 30, 3136 (1984).

[3] J. A. Sánchez-Gil, V. Freilikher, I. V. Yurkevich, and A. A. Maradudin, Phys. Rev. Lett. 80, 948 (1998); J. A. Sánchez-Gil, V. Freilikher, A. A. Maradudin, and I. V. Yurkevich, Phys. Rev. B. 59, 5915 (1999).

[4] J. A. Konrady, J. Acoust. Soc. Am. 56, 1687 (1974).

[5] Z. Tesanovic, M. Jaric, S. Maekawa, Phys. Rev. Lett. 57, 2760 (1986).

[6] N. Trivedi and N. W. Ashcroft, Phys. Rev. B. 38, 12298 (1988).

[7] G. A. Luna-Acosta, Kyungsun Na, L. E. Reichl, and A. Krokhin, Phys. Rev. E 53, 3271 (1996).

[8] N. M. Makarov and Yu. V. Tarasov, J.Phys.: Condens. Matter 10, 1523 (1998); Phys. Rev. B. 64, 235306 (2001).

[9] F. M. Izrailev, N. M. Makarov, and M. Rendón, Phys. Rev. B. 72, 041403(R) (2005).

[10] R. D. Mattuck, A Guide to Feynman Diagrams in the Many-Body Problem, 2nd edition, (Dover Publications, New York, 1992).

Received on 8 December, 2005

Publication Dates

• Publication in this collection
  29 Nov 2006
• Date of issue
  Sept 2006

History

• Received
  08 Dec 2005